拉普拉斯变换的定义 收敛域

拉普拉斯变换、连续时间系统的S 域分析基本要求通过本章的学习，学生应深刻理解拉普拉斯变换的定义、 收敛域的概念：熟练掌握拉普拉斯变换的性质、卷积定理的意义及它们的运用。

能根据时域电路模型画出S 域等效电路模型，并求其冲激响应、零输入响应、零状态响应和全响应。

能根据系统函数的零、极点分 布情况分析、判断系统的时域与频域特性。

理解全通网络、最小相移网络的概念以及拉普拉 斯变换与傅里叶变换的关系。

会判定系统的稳定性。

知识要点1. 拉普拉斯变换的定义及定义域(1) 定义 单边拉普拉斯变换：st正变换 [f(t)] F(s) 0 f(t)e dt双边拉普拉斯变换:的收敛域。

0与函数f(t)的性质有关。

2. 拉普拉斯变换的性质逆变换[F(s)] f(t)stF(s)e正变换F B(S )f(t)edt1 jst逆变换 f(t)2 jjF B(s)eds(2)定义域若0 时，lim f (t)et0则St 「 ” ”t ”f(t)e 在0的全部范围内收敛，积分0就是f(t)的单边拉普拉斯变换st[f2(t)] F2(S) , 1 , 2 为常数(2 ) 原函数微分若[f (t)] F(s)则[響]sF(s) f(0 ) dt[d df>] s n F(s) n1s nr1f(r)(0 ) dt r 0r式中f⑴(0 )是r阶导数在0时刻的取值。

dt r(3)原函数积分(4)延时性F (s)，则[f(t t°)u(t t。

)] e st0F(s)(5)s域平移at若[f (t)] F (s)，则[f(t)e ] F(s a)(6)尺度变换1 s若[f (t)] F (s)，则[f (at)] F( )( a 0)a a(7)初值定理lim f (t) f(0 ) limsF(s)to s(8)终值定理lim f (t) lim sF(s)t s(9)卷积定理若[f1(t)] F1(s)，[f2(t)] F2(S)，则有[f1(t) f2(t)] F1(S)F2(S) (1) 线性性［仏“⑴］1 1肓[h(s) F2(s)] = ^-j.h(p)F2(s p)dpj[i f l(t) 2f2(t)] 1F1(S) 2F2(S)t若[f (t)] F (s)，则[f(t)dt] F(s)s3 式中f(D(0)s f(t)dt若[f (t)]3.拉普拉斯逆变换(1 ) 部分分式展开法首先应用海维赛展开定理将F (s)展开成部分分式，然后将各部分分式逐项进行逆变换，最后叠加起来即得到原函数 f (t)。

拉普拉斯变换存在的条件拉普拉斯变换是一种数学工具，用于处理信号和系统的分析。

在应用拉普拉斯变换时，需要满足一定的条件，以确保变换的有效性和准确性。

以下是拉普拉斯变换存在的条件：1. 信号必须是因果的：这意味着信号在任何时刻都不会出现在未来的时间，即信号的响应只能依赖于过去或当前的输入。

因果性是信号处理中的基本原则之一，也是应用拉普拉斯变换的前提条件之一。

2. 信号必须是有界的：信号的幅度不能无限增长，否则会导致拉普拉斯变换无法收敛。

有界性是确保信号处理过程中能够得到合理结果的必要条件。

3. 信号必须是单侧的：在时域中，信号的定义范围只能是非负的。

这也是因果性的一种表现形式，保证信号的单侧性有利于信号处理和系统分析的准确性。

4. 初值必须存在：信号在初始时刻的值必须已知，以便进行拉普拉斯变换。

初值的存在性是确保拉普拉斯变换结果的准确性和可靠性的重要条件。

5. 频域中必须存在拉普拉斯变换：信号的频谱必须存在拉普拉斯变换，以便在频域中进行信号分析和处理。

这也是应用拉普拉斯变换的基本前提之一。

6. 分子次数小于分母次数：在拉普拉斯变换中，被变换函数的分子次数必须小于分母次数，以确保变换结果的存在和收敛性。

这是拉普拉斯变换的基本要求之一。

7. 收敛域必须存在：拉普拉斯变换的收敛域是指变换结果在何种条件下收敛的范围。

确保收敛域的存在是应用拉普拉斯变换时必须注意的条件之一。

8. 初值定理和终值定理成立：初值定理和终值定理是拉普拉斯变换中的重要定理，用于计算信号在初始时刻和稳态时刻的值。

这两个定理的成立是应用拉普拉斯变换的基础之一。

总的来说，拉普拉斯变换存在的条件是多方面的，涉及信号的性质、变换结果的准确性、收敛性等多个方面。

只有在满足这些条件的前提下，才能有效地应用拉普拉斯变换进行信号和系统的分析与处理。

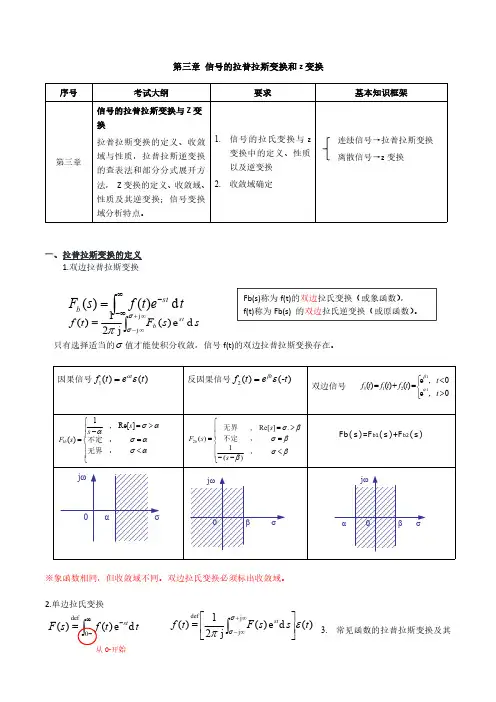
⎰∞∞--=t e t f s F st b d )()(⎰∞--=0def d e )()(t t f s F st)(d e )(j 21)(j j deft s s F t f st επσσ⎥⎦⎤⎢⎣⎡=⎰∞+∞-第三章信号的拉普拉斯变换和z 变换一、拉普拉斯变换的定义1.双边拉普拉斯变换只有选择适当的σ值才能使积分收敛，信号f(t)的双边拉普拉斯变换存在。

※象函数相同，但收敛域不同。

双边拉氏变换必须标出收敛域。

2.单边拉氏变换3.常见函数的拉普拉斯变换及其⎰∞+∞-=j j d e )(j21)(σσπs s F t f st b Fb(s)称为f(t)的双边拉氏变换（或象函数），f(t)称为Fb(s)的双边拉氏逆变换（或原函数）。

从0-开始收敛域二、拉普拉斯变换性质线性性质尺度变换证明：[]⎰∞--=de)()(tatfatf L st，则令atτ=时移特性与尺度变换相结合复频移（s域平移）特性时域的微分特性（微分定理）若f(t)←→F(s),Re[s]>σ0,则f’(t)←→sF(s)–f(0-)证明：()()()())(deedessFfttsft ftt f ststst+-=⎥⎦⎤⎢⎣⎡--='--∞-∞---∞-⎰⎰推广：()()[])0()0()()0(d)(d22----'--='--=⎥⎦⎤⎢⎣⎡fsfsFsffsF sttfL∑-=----=⎥⎦⎤⎢⎣⎡1)(1)0()(d)(d nrrrnnnfssFsttfL若f1(t)←→F1(s)Re[s]>σ1,f2(t)←→F2(s)Re[s]>σ2则a1f1(t)+a2f2(t)←→a1F1(s)+a2F2(s)Re[s]>max(σ1,σ2)若f(t)←→F(s),Re[s]>σ0，且有实数a>0，则f(at)←→)(1asFa若f(t)<----->F(s),Re[s]>σ0,且有实常数t0>0,则f(t-t0)ε(t-t0)<----->e-st0F(s),Re[s]>σ0若f(t)←→F(s),Re[s]>σ0,且有复常数s a=σa+jΩa,则f(t)e s a t←→F(s-s a),Re[s]>σ0+σas-→2：?)(sin ←→t t t ε=三、拉普拉斯逆变换三种方法：（1）查表（2）利用性质（3）部分分式展开-----结合∴......,,321为不同的实数根，n p p p p nn p s K p s K p s K s F -++-+-= 2211)(ip s i i s F p s K =-=)()()(e ]1[1t p s L t p i i ε=--若象函数F(s)是s 的有理分式，可写为1110111.......)(a s a s a s b s b s b s b s F n n n m m m m ++++++++=----若m ≥n （假分式）,可用多项式除法将象函数F(s)分解为有理多项式P(s)与有理真分式之和。

信号与系统的拉普拉斯变换是一种数学工具，用于分析线性时不变系统的行为。

它通过将信号或系统表示为复指数的线性组合，将时间域的信号或系统转换为频域表示。

在频域中，系统的性质可以更容易地理解和分析。

拉普拉斯变换具有收敛域的性质，这是其定义的一部分。

收敛域是复平面上使得拉普拉斯变换存在的点。

此外，拉普拉斯变换具有一些重要的性质，包括线性性质、时移性质、频移性质、微分性质和积分性质等。

这些性质在分析系统时非常有用。

此外，拉普拉斯变换在分析线性时不变系统的稳定性方面具有重要作用。

通过分析系统的极点和零点分布，可以确定系统的稳定性。

极点和零点是系统函数的根，它们在复平面上的位置决定了系统的动态行为。

总之，信号与系统的拉普拉斯变换是理解和分析线性时不变系统的重要工具，它可以转换时间域的信号或系统到频域表示，提供了一种方便的方式来理解和分析系统的动态行为和稳定性。