第二章《二次函数回顾与思考》(2)
- 格式:ppt
- 大小:561.00 KB
- 文档页数:16

【教学目标】1.复习和巩固二次函数的基本概念和性质;2.通过回顾,检查学生对二次函数的理解程度,并帮助学生弄清关键概念和解题思路;3.培养学生的分析、解决问题的能力,培养学生的逻辑思维和抽象思维。
【教学重点】1.梳理二次函数的基本概念和性质;2.提供典型例题,帮助学生掌握解题思路;3.引导学生探究二次函数的应用领域。
【教学难点】1.通过合理的引导和问题导向,帮助学生运用所学知识解决实际问题;2.让学生了解二次函数在自然界和社会生活中的应用。
【教学过程】【导入】引入二次函数的概念:放映一段优秀的科普视频,引起学生对二次函数的兴趣,并回顾二次函数的定义和性质。
【讲授】1.复习与总结回顾并总结二次函数的定义、一般式、顶点式、轴对称式等表示方法,并归纳总结二次函数的性质。
2.典型例题讲解提供一些典型的二次函数问题,帮助学生巩固概念,并引导学生掌握解题思路和方法,例如:例题1:已知函数f(x) = ax^2 + bx + c的顶点是(1, -2),且经过点(-1, 4),求a、b、c的值。
例题2:若抛物线y = ax^2 + 2ax - 3与x轴交于点A、B,交点A在点(-1, 0)的左边,且AO是x轴的中线,求a的取值范围。
3.实际应用通过介绍二次函数在自然界和社会生活中的应用,引导学生了解二次函数在实际问题中的作用。
例如:抛物线的运动轨迹、桥梁的设计、物体自由落体的运动等。
【练习】对所学知识进行巩固与运用,提供一些练习题,检查学生对二次函数的理解和应用能力。
【拓展】引导学生进一步探索,拓宽知识面,例如引导学生理解二次函数图象的平移、伸缩等变化。
【归纳总结】通过本节课的学习,学生总结本节课的重点内容和解题方法,归纳反思学习中出现的问题和不足之处。
【课堂小结】对本节课的学习内容进行总结,引导学生思考并提问,对学生的学习情况进行梳理和分析。
【作业布置】布置一些练习题作为课后作业,巩固所学知识,并提醒学生及时复习课堂内容。
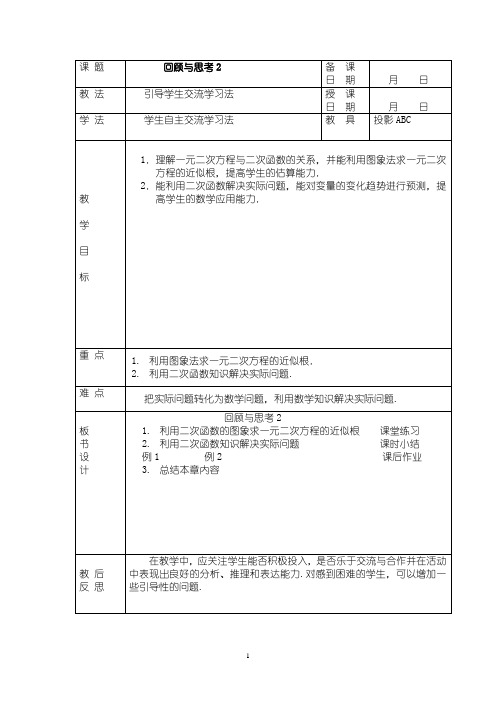
教 学 过 程一.创设问题情景,引入新课上节课我们回顾了二次函数的定义,二次函数的三种表示方式,重点研究了不同形式的二次函数的图象与性质.本节课我们继续来回顾利用二次函数的图象求一元二次方程的近似根和利用二次函数知识解决实际问题.二、讲解新课:1. 利用二次函数的图象求一元二次方程的近似根一元二次方程)0(02≠=++a c bx ax 和二次函数)0(2≠++=a c bx ax y 的关系.在二次函数)0(2≠++=a c bx ax y 中,当y=0时,就转化成了一元二次方程)0(02≠=++a c bx ax ,因此可以说一元二次方程)0(02≠=++a c bx ax 是函数)0(2≠++=a c bx ax y 的一种特殊情况,即函数值为0的情况,这时函数中自变量x 的值就是方程的解.所以,当二次函数)0(2≠++=a c bx ax y 的图象与 x 轴有交点时,二次函数)0(2≠++=a c bx ax y 的图象与 x 轴的交点的横坐标就是一元二次方程)0(02≠=++a c bx ax 的根.在不画图象的情况下,能否判断二次函数)0(2≠++=a c bx ax y 的图象与 x 轴是否有交点呢?当042>-ac b 时,抛物线与x 轴有两个交点;当042=-ac b 时,抛物线与x 轴只有一个交点;当042<-ac b 时,抛物线与x 轴没有交点.在不画图象的情况下,判断下列二次函数的图象与 x 轴的交点情况.(1)322--=x x y , (2)322+-=x x y , (3)442++=x x y 能否判断方程0322=--x x ,0322=+-x x ,0442=++x x 的解的情况呢?例1 利用二次函数的图象求一元二次方程01522=-+x x 的近似根. (答案:-3,2.5)2. 利用二次函数知识解决实际问题例2 课本复习题A 组第7题例3 某产品每件的成本是120元,试销阶段每件产品的销售价x(元)与产品的日销售量y (台)之间的关系是y =-x+200,为获得最大销售利润,每件产品的销售价应定为多少元?此时每日的销售利润是多少?3. 总结本章内容y=x 2,y=-x 2y=ax 2,y=ax 2+c y=a(x-h)2+k,y=ax 2+bx+c 一元二次方程与二次函数的关系利用二次函数的图象求一元二次方程的近似根刹车距离何时获得最大利润最大面积是多少二次函数的对称轴和顶点坐标公式用多种方式表示二次函数的定义实际问题情境一元二次方程与二次函数用二次函数解决实际问题二次函数的图象二次函数所描述的关系二次函数三、课堂练习某类产品按质量共分为10个档次,生产最低档次产品每件利润为8元,如果每提高一个档次每件利润增加2元.用同样的工时,最低档次产品每天可生产60件,每提高一个档次将少生产3件,求生产何种档次的产品利润最大?四、课时小结这节课我们巩固了三大内容:利用二次函数知识解决实际问题;利用二次函数的图象求一元二次方程的近似根;本章的知识结构图.四、课后作业复习题B 组题。

顾与思考1. 你在哪些情况下见到过抛物线的“身0 ?用语皆或J开进行描述.2. 你能用二次函数的知识解决哪些实际问题?与同伴交流.3.{象的方法.4.1象有哪些性质?如何确定它的开口方向,对称轴和顶点坐标?讲用具体例子进行说明.九年级數学(下)第二章《二次因數》第二章《回顾与思考》二次函数小结想一叫Ta顾与思考5.用具体例子说明如何莫?恰当或更有效地利用二次函数的表达式,表格和图象刻画变量之间的关系. 6•用自己的语皆描述二次函数y=ax2+bx+c的图象与方程ax2+bx+c=0的根之间的关系.2bd X ---------(2a函数y=ax2+bx+t 的顶点式2 4ac-b 2cH ----------------- t4a • ■一般地,对于二次函数y=ax 2+bx+c,我们可以利用配方法 推导出它的对称轴和码点坐标.y 二 ax 2+ bx+c ( 1 \2—U X H ------ X + C )、2ct 丿 4«2 4ac-b 例.求次函数y=ax 2+bx+c 的对称轴和顶点坐标・ 1・配方:这个结果通 常称为求顶 V a (2 b H ——x+aX H --- I la(b} =a x-\ ----- I la) /2 + 4a提取二次项系数配方:加上再 减去一次项系 + C 数绝对值一半 的平方整理:前三项化为平方形 式,后两项合并同类项 化简:去掉中括号Q越一赳P49[卜函数丫=3x Ubx+c的图象?我们知道,作出二次函数y=3x2的图象,通过平移抛物线y二3x2可以得到二次函数y二3x2 - 6x+5的图象.怎样直接作出函数y=3x2-6x+5的图象?!.配方尸3(宀2也)+5勰器;需=3[(兀_1)2_"+5 =3(x — 1)2 +2.整理:前三项化为平方形式,化简:去掉中括号Q赳一赳出真r知直接画函数丫=ax2+bxM的图象?2. 根据配方式(顶点式)确定开口方向,对称轴,顶点坐标.Va=3>0, 开口向上;对称轴:直线x=l;顶点坐标:(1, 2). 3. 列表:根据对称性,选取适当值列表计算.4.画对称轴,描点,连线:作出二次函数ys3(x-ip+2 的图象.做一做P50Q( b \ y = a 兀 ---------I 2d 丿此,二次函^cy=ax 2+bx+c 的 图象是一条抛物线 它的对称轴是直线X = ---------------- ・2a务顶点坐标公式24ac — b 2H ----------------------4a(b 4ac - b?、9 2/ 4a 丿9w 它的顶点是-做一做p二誓小试牛刀确定下列二次函数图象的对称轴和顶点坐标:二次函«fcy=ax 2+bxtc (a^O)的图象和性质1 •顶点坐标与对称轴2 .位置与开口方向3 .增减性与最值 根据图形填表:抛物线 Iy=ax 2+bx+c(a>0)y=ax 2+bx+c(a<0)顶点坐标b 4ac — b~ ]b 4ac — b~ 2〃,4〃 )2a 4/7对称轴 位置 由a ,b 和c 的符号确定由a ,b 和c 的符号确定开口方向 向上向下增减性 在对称轴的左侧,y 随着x 的增大而减小. 在对称轴的右侧,y 随着x 的增大而增大. 在对称轴的左侧,y 随着x 的增大而增大. 在对称轴的右侧,y 随着x 的增大而减小.最值当2—2时,最小值为兰—______ 2" 4c当一汕,最大值为4宀7,1 2 37627二次函4fcy=ax2+bx+c (a=#0)与丫二宓?的关系仁相同点:⑴形状相同(图像都是抛物线,开口方向相同).(2) 都是轴对称图形.(3) 都有最(大或小)值.⑷a>0时,开口向上,在对称轴左侧,y都随x的增大而减小,在对称轴右侧,y都随x的增大而增大. a<0时,开口向下,在对称轴左侧,y都随x的增大而增大,在对称轴右侧,y都随x的增大而减小.二次函数y 二ax2+bx+c (a#=0)与y 二ax?的关系2 •不同点:(1)位置不同. ..(b 4ac-b2}⑵顶点不同:分别是和(ao).⑶对称轴不同:分别是兀=-2和y轴(xR)・2a(4)最值不同:分别是4。


北师大版九年级数学下册:2《二次函数——回顾与思考》教学设计一. 教材分析《二次函数——回顾与思考》这一节主要是让学生回顾已学的二次函数知识,通过对已学知识的梳理,加深对二次函数的理解,并为后续的学习打下基础。
教材中包含了二次函数的图像、性质、以及解决实际问题等方面的内容。
本节课的内容与学生的生活实际紧密相连,有利于激发学生的学习兴趣。
二. 学情分析九年级的学生已经学习了一定程度的数学知识,对二次函数有一定的了解。
但是,部分学生可能对二次函数的图像和性质理解不深,解决实际问题的能力较弱。
因此,在教学过程中,教师需要关注这部分学生的学习需求,通过合理的教学设计,帮助他们巩固已学的知识,提高解决问题的能力。
三. 教学目标1.让学生回顾和巩固二次函数的基本知识,理解二次函数的图像和性质。
2.培养学生解决实际问题的能力,提高学生运用数学知识分析问题和解决问题的能力。
3.激发学生学习数学的兴趣,培养学生的数学思维。
四. 教学重难点1.重点:二次函数的图像和性质,解决实际问题。
2.难点:对二次函数图像和性质的理解,以及运用二次函数解决实际问题的方法。
五. 教学方法1.讲授法:教师通过讲解,引导学生回顾和巩固二次函数的基本知识。
2.案例分析法:教师通过分析实际问题,引导学生运用二次函数解决实际问题。
3.小组讨论法:学生分组讨论,共同解决问题,培养学生的合作能力。
六. 教学准备1.教学课件:教师准备与本节课内容相关的课件,以便引导学生回顾和巩固二次函数的基本知识。
2.实际问题:教师准备一些与生活实际相关的数学问题,引导学生运用二次函数解决实际问题。
七. 教学过程1.导入(5分钟)教师通过提问的方式,引导学生回顾已学的二次函数知识,如二次函数的定义、图像、性质等。
同时,教师也可以让学生举例说明二次函数在实际生活中的应用,激发学生的学习兴趣。
2.呈现(10分钟)教师通过课件展示二次函数的图像和性质,让学生直观地感受二次函数的特点。

第二讲二次函数㈠承上启下 知识回顾问题1、现有一根12m 长的绳子,用它围成一个矩形,如何围法,才使举行的面积最大?问题2、很多同学都喜欢打篮球,你知道吗:投篮时,篮球运动的路线是什么曲线?怎样计算篮球达到最高点时的高度?这些问题都可以通过学习二次函数的数学模型来解决,今天我们学习“二次函数”㈡紧扣考点 专题讲解请用适当的函数解析式表示下列问题中情景中的两个变量y 与x 之间的关系:(1) 面积y (cm 2)与圆的半径 x ( cm )(2)王先生存人银行2万元,先存一个一年定期,一年后银行将本息自动转存为又一个一年定期,设一年定期的年存款利率为文 x 两年后王先生共得本息y 元;(1)y =πx 2(2)y = 2000(1+x)2 = 20000x 2+40000x+20000 上述三个函数解析式具有哪些共同特征?归纳总结:上述三个函数解析式经化简后都具y=ax ²+bx+c (a,b,c 是常数, a ≠0)的形式.我们把形如y=ax ²+bx+c(其中a,b,C 是常数,a ≠0)的函数叫做二次函数(quadratic funcion) 称a 为二次项系数, b 为一次项系数,c 为常数项,1、下列函数中,哪些是二次函数? (1)2x y = (2) 21xy -= (3) 122--=x x y(4) )1(x x y -= (5))1)(1()1(2-+--=x x x y答:1.3.4.2、分别说出下列二次函数的二次项系数、一次项系数和常数项:(1)12+=x y (2)12732-+=x x y (3))1(2x x y -= 二次函数1 二次函数3 二次函数 -2 一次项系数0 一次项系数7 一次项系数 2 常数项1 常数项 -12 常数项03、若函数mm x m y --=2)1(2为二次函数,则m 的值为 2 。
例1、已知二次函数 q px x y ++=2当x=1时,函数值是4;当x=2时,函数值是-5。