电源的等效变换练习题

格式：docx
大小：36.80 KB
文档页数：3

下载文档原格式

高中物理电学部分电路等效变换练习题(含答案)精选全文

可编辑修改精选全文完整版1、计算下列各电路图的等效电阻R ab（电阻单位：Ω）（a）（b）（c）（d ）2、下图中Ω=Ω====60030054321R R R R R ，，求开关S 断开和闭合时a 和b 之间的等效电阻。

（a ）（b ）3、求下图电路的等效电阻R ab ，其中Ω==121R R 。

4、，，，，，）电路中，在下图（Ω=Ω=Ω===k 2k 6k 1262432121R R R V U V U a S S 图（b ）为经电源变换后的等效电路。

（1）求等效电路的Is 和R ；（2）根据等效电路，求R3中的电流和消耗功率；（3）分别在图（a ）和图（b ）中求出R1、R2及R3消耗功率；（4）试问Us1、Us2发出的功率是否等于Is 发出的功率？R1、R2消耗的功率是否等于R 消耗的功率？为什么？（a ）（b ）5、求下图各电路中的I和U ab。

（电阻单位：Ω）（a）（b）6、利用叠加原理和支路电流法求下图电路中各支路电流，并校验功率是否平衡。

（电阻单位：Ω）7、计算下图电路中的电流I1、I2。

8、在下图电路中，已知：Ω=Ω=Ω====43129132121R R R V U V U A I S S S ，，，，，Ω=84R 。

试用电压源与电流源等效变换的方法，计算R 4与U s2串联支路中的电流I 4。

9、用回路电流法求下图电路中电流I 。

（电阻单位：Ω）10、试用戴维宁定理计算下图电路中的电流I ab ，并用基尔霍夫定律检验计算结果。

（电阻单位：Ω）11、试用电源等效变换法求下图电路中的电流I。

（电阻单位：Ω）12、求下图电路中流过电阻R L的电流I L。

（电阻单位：Ω）13、如下图电路中，已知：Ω==Ω==Ω======3,2,9,2,4,10,3,9524314321R R R R R A I V U V U V U V U S S S S S Ω=66R 。

用戴维宁定理求电流I 。

03 电源的等效变换和网孔电流法

us1
+
_
us
i
.+
.
.
sk
.
u s u s1 u s 2 u s 3
u
电路
南京理工大学电光学院
2. 1.3 电压源、电流源的串联和并联
电压源的并联
同极性、同数值并联
+
.
+ us _ + us _
.
+ us _
us _
.
.
电路
南京理工大学电光学院
2. 1.3 电压源、电流源的串联和并联
电路
南京理工大学电光学院
运用等效变换分析含受控源的电阻电路
例: 求输入电阻重点解: 输入电阻：R in 另解:
a i
2Ω
u i
a
.
+ u _
i
2Ω
+ u1 _
2Ω
u1
b.

u 1 2 1.5 u 1 u1 2
8
.
+ u _
2Ω
+ u1 _
+ u1 _
+ _ 2u1
R in
例、电流I。
+ 24V _ 6Ω 6Ω I 3Ω + 3V _ 4A 6Ω I 6Ω 3Ω 1A
I
6Ω 2Ω
5A
I
2 26
5 1.25 A
注意: 未知量所在的支路一般保持不动
电路南京理工大学电光学院
2.5 实际电源的等效变换
例: 运用电源等效变换方法求u
2Ω
2Ω
3Ω
_
6V
+
4Ω

第五节-两种电源模型的等效变换(1)

三、两种实际电源模型之间的等效变换
实际电源可用一个理想电压源 US 和一个电阻 R0 串联的电路模型表示，其输出电压 U 与输出电流 I 之间关系为
U = US R0I
实际电源也可用一个理想电流源 IS 和一个电阻 RS 并联的电路模型表示，其输出电压 U 与输出电流 I 之间关系为
U = RSIS RSI
如图 3-21 所示：等效电流源的
电流 IS IS1－IS2 3 A，其等效内阻为 R R1∥R2 2
(3)求出 R3中的电流
I3
R R3 R
IS 0.5 A
图 3-21 例题 3 -7 的最简等效电路
2012年高考题
本章小结
一、基夫尔霍定律二、支路电流法三、叠加定理四、戴维宁定理五、两种实际电源模型的等效变换
+
US
+
-
US2 -
b
b
3、两个实际电压源串联，可以用一个等效的电压源替代，替代的条件是
US = US1 + US2 R0 = R01 + R02
四、等效变换的类型
等效为电流源 1、与恒流源串联的元件不作用，可等效成该恒流源；
例题：
R IS
IS
+
US-
a
b (a) a b (b)
a
IS b
以各支路电流为未知量，应用基尔霍夫定律列出节点电流方程和回路电压方程，解出各支路电流，从而可确定各支路(或各元件)的电压及功率，这种解决电路问题的方法叫做支路电流法。
对于具有 b 条支路、n 个节点的电路，可列出 (n 1) 个独立的电流方程和 b (n 1) 个独立的电压方程。
三、叠加定理

电压源与电流源的等效变换.

【练习与思考】
把如图所示的电压源变换成电流源，电流源变换成电压源
+ _ a 6V _ + 9V a a a 2A b
2Ω
（ a） b
3Ω
（b） b
3A
1Ω
5Ω
b
（ c）
（d）
例1:
试用电压源与电流源等效变换的方法计算2电阻中的电流。 1 2A 1 12V (a) 2 + 解: –
1 1
注意事项： 1）电压源和电流源的等效关系只对外电路而言，对电源内部则是不等效的。例：当RL= 时，电压源的内阻 R0 中不损耗功率，而电流源的内阻 R0 中则损耗功率。 2）等效变换时，两电源的参考方向要一一对应。 a a + – E E – + IS R0 R0 R0 b b 3）理想电压源与理想电流源之间无等效关系。 4）任何一个电动势 E 和某个电阻 R 串联的电路，都可化为一个电流为 IS 和这个电阻并联的电路。 a IS b R0 a
2
4V 2A
6
+ 1
I
4
2 2
4 1A
I
1
I
4A
解：
2 2 4 1A
2
I
1
8V
+ -
4 1A 2
I
1
4A
I
2A 1A 4 4 1 3A 2
I
1
2 I 3 2A 21
– 电流源 0
E IS Ro I
E IS Ro I
对外电路来说, 电压源和电流源可以互相等效
I + E R0 电压源由图a： U = E－ IR0 E = ISR0 等效变换条件:

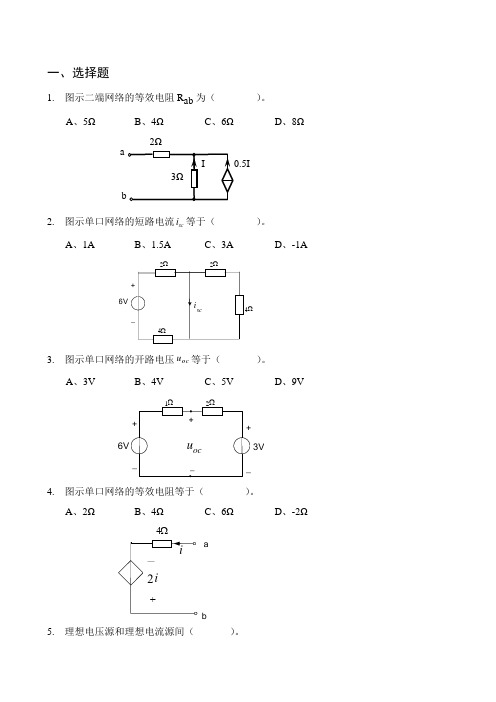
电路_第四章练习

一、选择题1. 图示二端网络的等效电阻R ab 为（）。

A 、5ΩB 、4ΩC 、6ΩD 、8Ω2. 图示单口网络的短路电流sc i 等于（）。

A 、1AB 、1.5AC 、3AD 、-1A3. 图示单口网络的开路电压oc u 等于（）。

A 、3VB 、4VC 、5VD 、9V4. 图示单口网络的等效电阻等于（）。

A 、2ΩB 、4ΩC 、6ΩD 、-2Ω5. 理想电压源和理想电流源间（）。

6 V 3 V6 V ΩΩ4 abA 、有等效变换关系B 、没有等效变换关系C 、有条件下的等效关系6. 图示电路中a 、b 端的等效电阻R ab 在开关K 打开与闭合时分别为（）。

A 、10Ω，10ΩB 、10Ω，8ΩC 、10Ω，16ΩD 、8Ω，10Ω7. 图示电路中A 、B 两点间的等效电阻与电路中的R L 相等，则R L 为（）。

A 、40 ΩB 、30 ΩC 、20 Ω A B R L Ω10 Ω60 Ω30 Ω....二、填空题1. 具有两个引出端钮的电路称为网络，其内部含有电源称为网络，内部不包含电源的称为网络。

2. “等效”是指对以外的电路作用效果相同。

戴维南等效电路是指一个电阻和一个电压源的串联组合，其中电阻等于原有源二端网络后的电阻，电压源等于原有源二端网络的电压。

3. 在进行戴维南定理化简电路的过程中，如果出现受控源，应注意除源后的二端网络等效化简的过程中，受控电压源应处理；受控电流源应处理。

在对有源二端网络求解开路电压的过程中，受控源处理应与分析方法相同。

4. 直流电桥的平衡条件是相等；负载获得最大功率的条件是等于，获得的最大功率max P = 。

5. 两种实际电源模型等效变换是指对外部等效，对内部并无等效可言。

当端子开路时，两4Ω4Ω1616Ka b电路对外部均不发出功率，但此时电压源发出的功率为，电流源发出的功率为；当端子短路时，电压源发出的功率为，电流源发出的功率为。

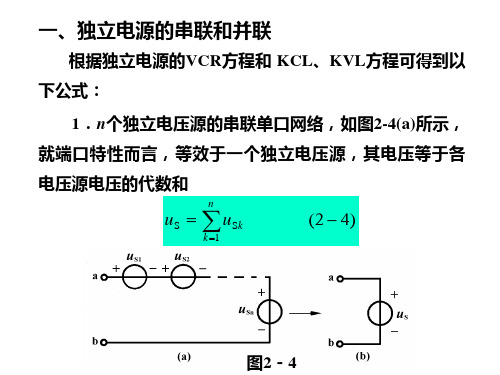
2-3电源的等效变换

例2－8 求图2-14(a)电路中电流i 。
图2－14
解：可用电阻串并联公式化简电路。具体计算步骤如下：先求出3和1电阻串联再与4电阻并联的等效电阻Rbd
Rbd
4(3 1) 2 4 3 1
得到图(b)电路。再求出6和2电阻串联再与8并联的等效电阻Rad
Rad
求单口网络的VCR方程,并画出单口的等效电路。
图2－8
解：在端口外加电流源i，写出端口电压的表达式
u u S R1 (iS i) R2 i ( R1 R2 )i u S R1iS
其中:
Ro i u oc
Ro R1 R 2 2 3 5 u oc u S R1i S 6V 2 2A 10V
图2－7
图2－7
解：为求电流i1和i3，可将三个并联的电流源等效为一个电流源，其电流为
iS iS1 iS2 iS3 10A 5A 1A 6A
得到图(b)所示电路，用分流公式求得：
i1 G1 1 iS 6A 1A G1 G 2 G3 1 2 3
一、独立电源的串联和并联
根据独立电源的VCR方程和 KCL、KVL方程可得到以下公式：
1．n个独立电压源的串联单口网络，如图2-4(a)所示，
就端口特性而言，等效于一个独立电压源，其电压等于各电压源电压的代数和
uS uSk
k 1
n
(2 4)
图2－4
图2－4
uS uSk
k 1
例2－10 求图2-16(a)电路中电压u。
图2－16
解：(1)将1A电流源与5电阻的串联等效为1A电流源。20V 电压源与10电阻并联等效为20V电压源，得到图(b)电路。

西南交大网络教育离线作业

11.试用电源的等效变换法求如图2-73所示电路中的电流I。

解：根据电路结构，逐步进行电源的等效变换，如图所示所以，电流12.试用电源的等效变换法求如图2-76所示电路中的电流I和电压U AB。

解：（1）用电源等效变换法求出电流I。

（含未知电流I支路不变，将其余电路部分等效变换等电压源，整个电路将变成单回路电路）等效变换化简如图所以，电流由原电路，有13.试用叠加定理求解题2.7中的电流I，并检验电路的功率平衡。

解：运用叠加原理，每个电源单独作用时的电路及参数如下（1）8V电压源单独作用时的电路如图所示有，电流（2）10V电压源单独作用时的电路如图所示有，电流(3)2V电压源单独作用时的电路如图所示有，电流所以，由叠加原理，有14.试用戴维南定理求如图2-79所示电路中的电流I。

解：第一步：找出二端网络将待求电流I所在的支路移去，二端网络如图第二步：求二端网络的开路电压U AB易知，电压第三步：求等效电阻R O对应无源二端网络如图故，等效电阻第四步：求待求参数电流I4Ω3VAB2ΩI10V画出戴维南等效电路，如图所以，电流15.已知图5-62所示电路中电感，试分析题5.1中当时电路的、和，并画出电流的波形图。

解：‘三要素法’（1）求初始值由题5.1的解可知初始值（2）求稳态值t=∞(∞)(∞)(∞)换路后的稳态电路如下图所示由图可得其中：为换路后的电路中去掉电感L后的二端网络的等效电阻。

所以波形图如下图：16.如图5-70所示电路中，已知，，，，换路前电路已处于稳态，时开关S闭合，试求时路中的和。

解：‘三要素法’（1）求初始值根据换路前的稳态电路（电容断路），有时刻的等效电路如图所示由图可得（2）求稳态值t=∞换路后的稳态电路如下图所示由图可得（3）求时间常数由换路后的电路，有所以17.使异步电动机自己转动起来的基本条件是什么？简述异步电动机的转动原理。

答：异步电动机自己转起来的基本条件是：（1）、定子绕组通入三相交流电流，在气隙中产生旋转磁场；（2）、转子绕组自成回路。

电源及电阻的等效变换

思考：电流源能否串联？ X
10
第
电压源与二端网络N并联，电流源与二端网络N串联页
• 对于外电路而言，电
i
压源与任意二端网络N

并联都可等效为电压
uS
Nu
源本身。

i

uS
u

•对于外电路而言，电流源与任意二端网络
串联的等效电路就是电流源本身。
i N
is

u

i
is

u

X
4.实际电压源模型与实际电流源
1
1. 等效的基本概念必须掌握！
第页
等效(equivalence): 如果一个单口网络N和另一个单口网络N’端口处的电压电流关系完全相同，
即他们在平面上的伏安特性曲线完全重合，则称这两个单口网络是等效的。
i
N1
u
M
i
N2
u
M
注意：等效是指对任意外电路而言，且等效指的是对外等效，对内不等效。
分流电流公式
i1

G1 G
i
i2

G2 G
i
in

Gn G
i
即按电导值正比分流。
X
5
2. 电阻元件的等效变换
第页
串并
对偶关系： R G iu 分压分流
X
6
2. 电阻元件的等效变换
第页
2.3 T-（Y-)型等效变换
1
+ us
-
Rs
R31
3 R23
R12
1
i1
R1
R2
i2
2 i1' 1

§1-9 电源的等效变换

u
B
⇒
3A
5Ω
u
B
⇒
5Ω
+ 15V 15 -
u
- B
X
几点说明
(1) 两种电源模型对于原电路可以等效替代，对外两种电源模型对于原电路可以等效替代，负载提供相同的功率，但电源内部不等效。负载提供相同的功率，但电源内部不等效。在上例的AB端口接上一负载电阻在上例的端口接上一负载电阻 RL = 4Ω A 通过运算可知：通过运算可知： + 电 R = 4Ω u 对于原电路，对于原电路，电压源模型和电 − 源的吸收功率均为：流模型计算 RL 的吸收功率均为： B 2 2 100 15 5 PL = W ×4 = 3 ×4 = 9 5+ 4 4+5 电压源电流源
X
所示电路，求电流i和受控电压源发出的功率。
1Ω Ω
i
3Ω Ω
6V
+ u −
2Ω Ω
0.5u
解答
2 u= 6 = 4V 1+ 2
4 6 = 3i + 0.5u = 3i + 0.5 × 4 = 3i + 2 ⇒ i = A 3
• 受控源发出的功率 P = −0.5ui = − 8 W
3
工程应用——散热风扇的速度控制散热风扇的速度控制工程应用
3 Ω 7
1 V 7
（c）
i
+
u
-
（d）
X
等效电路的另一个例子
例：试解释如下电路的等效原理。
例题4 求图（所示单口网络的等效电阻。例题求图（a）所示单口网络的等效电阻。
先将电路等效变换为如图解：所示，由图可得：（b）所示，由图可得：

电源等效变换法练习题

电源等效变换法练习题在电路分析中，电源等效变换法是一种常用的方法。

它的基本思想是将电源及其产生的电流电压转化为等效的电流源或电压源，以简化电路分析。

本文将通过一些练习题来说明电源等效变换法的应用。

1. 电流源转换为电压源考虑一个电路，其中有一个1A的电流源与电阻R并联。

我们希望将这个电流源转化为等效的电压源。

首先，根据欧姆定律，电流源与电阻并联，我们可以得到电环路方程：1A = I + V/R，其中I为等效的终端电流，V为等效的电压源电压。

我们可以将电流源等效为电压源的内阻，假设为Ri，那么根据欧姆定律，我们可以得到等效电压源的电压方程：V = Ri * I。

联立以上两个方程，可以解得：V = 1V，Ri = R。

因此，1A的电流源可以等效为1V的电压源，内阻为R的电路。

2. 电压源转换为电流源现在考虑一个电路，其中有一个5V的电压源与电阻R串联。

我们希望将这个电压源转化为等效的电流源。

根据基尔霍夫电压定律，我们可以得到电压源与电阻串联时的电路方程：5V = I * R + V，其中I为等效的电流源电流，V为等效的绂端电压。

我们可以将电压源等效为电流源的内阻，假设为Ri，那么根据基尔霍夫电压定律，我们可以得到等效电流源的电流方程：I = (5V - V) / Ri = 5V / Ri。

联立以上两个方程，可以解得：I = 5V/R，Ri = R。

因此，5V的电压源可以等效为5V/R的电流源，内阻为R的电路。

3. 电路分析示例现在我们来看一个具体的电路分析示例，以进一步理解电源等效变换法。

假设有一个电路，其中有一个1A的电流源与一个5Ω的电阻串联，再与一个10V的电压源并联。

我们希望求解该电路中的电流和电压。

首先，我们可以将电流源和电压源转换为等效的电压源和电流源。

根据上面的分析，电流源可以等效为1V的电压源，内阻为5Ω。

电压源可以等效为10V/5Ω=2A的电流源，内阻为5Ω。

然后，我们可以将等效的电压源和电流源与电阻进行串并联的简化电路分析。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

电源的等效变换练习题
电源是电路中不可或缺的组成部分，对于电路的正常运行起着重要的作用。

而了解电源的等效变换对于电子工程师和电路设计者来说同样是非常重要的。

下面我将给大家提供一些关于电源等效变换的练习题，帮助大家更好地理解和掌握这一概念。

练习题一：串、并联电源的等效变换
1. 若有两个串联电源，电源1电动势为E1，内阻为r1；电源2电动势为E2，内阻为r2。

请计算串联电源的等效电动势和等效内阻。

答案：
等效电动势 E = E1 + E2
等效内阻 r = r1 + r2
2. 若有两个并联电源，电源1电动势为E1，内阻为r1；电源2电动势为E2，内阻为r2。

请计算并联电源的等效电动势和等效内阻。

答案：
等效电动势 1/E = 1/E1 + 1/E2
等效内阻 1/r = 1/r1 + 1/r2
练习题二：电源的降压变换
3. 一台电源的电动势为E，内阻为r。

请计算通过一个外阻为R的电路后，电源的电压降和等效内阻。

答案：
电压降 V = E * ( R / (R + r) )
等效内阻 r' = r * ( R / (R + r) )
练习题三：电源的升压变换
4. 一台电源的电动势为E，内阻为r。

请计算通过一个外阻为R的电路后，电源的电压升和等效内阻。

答案：
电压升 V = E * ( (r + R) / r )
等效内阻 r' = r * ( R / (r + R) )
练习题四：电源的变压变换
5. 若有一台电动势为E1的电源，内阻为r1，通过一个变压比为k 的变压器连接到电阻为r2的电路上。

请计算电路的等效电动势和等效内阻。

答案：
等效电动势 E = E1 * k
等效内阻 r = (r1 * r2) / (r1 + (k^2 * r2))
通过以上练习题的学习，相信大家对于电源的等效变换有了更深入的理解。

电源的等效变换在电路设计中起着至关重要的作用，可以帮
助我们更好地分析和计算电路的性能。

希望大家能够将这些知识应用于实际的电路设计中，提高自己的技能和水平。

最后，希望大家继续努力学习电子工程知识，为电子行业的发展做出贡献！。