两种电源的等效变换
- 格式:ppt
- 大小:133.50 KB
- 文档页数:14


第三章复杂直流电路
---两种电源模型及其等效变换
一.填空
1.为电路的电源称为电压源,如果电压源内阻为,电源将提供,则称为理想电压源简称恒压源。
为电路的电源称为电流源,如果电流源内阻为,电源将提供,则称为理想电流源简称恒流源。
2.电压源与电流源的等效变换中对等效,对不能等效。
3.电压源变换为等效电流源的公式为,内阻R0的数值,改为联;电流源变换为电压源的公式为内阻r的数值,改为联;
4.两种电源模型的等效变换时,I
S 与U
S
的方向应当一致,即I
S
的端与U
S
的应互相对应。
二.是非判断
1.恒压源和恒流源之间也能等效变换。
()
2.理想电流源的输出电流和电压都是恒定的,是不随负载而变化的。
()
3.理想电压源的输出电流和电压都是恒定的,是不随负载而变化的。
()三.将下图中的电流源和电压源进行互换
四.计算
1.用电压源与电流源等效变换法,求图所示电路中流过R的电流。
其中E1=E2=3V,E3=9V,R1=R2=R3=3Ω,R=1Ω。
2.利用电源的等效变换计算图中的电流I
3。
3.试用电压源与电流源等效变换的方法计算图中2Ω电阻中的电流I。

2-2 试用电压源与电流源等效变换的方法计算题图2-2中3Ω电阻中的电流I 。
解:根据题目的要求,应用两种电源的等效变换法,将题图2-2所示电路按照解题图12所示的变换顺序,最后化简为解题图12(j)所示的电路,电流I为注意:(1) 一般情况下,与理想电流源串联的电阻可视为短路、而与理想电压源并联的电阻可视为开路。
故题图2-2所示电路最左边支路中的2Ω电阻可视为0;(2)在变换过程中,一定要保留待求电流I的支路不被变换掉;(3)根据电路的结构,应按照a-b、c-d、e-f的顺序化简,比较合理。
2-3 计算题图2-3中1Ω电阻上的电压U ab。
解:该题采用两种电源的等效变换法解题比较简便。
按照解题图13的顺序化简,将题图2-3所示的电路最后化简为解题图13(e)所示的电路,根据电阻串联电路分压公式计算电压U ab为2-5 应用支路电流法计算题图2-5所示电路中的各支路电流。
解:首先对于题图2-5所示电路的三条支路电流分别确定参考方向,如解题图15所示。
然后应用基尔霍夫电流定律和基尔霍夫电压定律定律列出下列三个方程:解之,得2-6 应用支路电流法计算题图2-6所示电路中的各支路电流。
解:如题图2-6所示,电路中的四条支路均为并联,其中一条支路电流为已知,根据支路电流法可知,只需列出三个独立方程即可求解。
为看图方便,将电路中4Ω电阻支路改画到解题图16所示的地方,应用基尔霍夫电流定律对结点a列出一个电流方程,再应用基尔霍夫电压定律对电路左边回路和中间回路列出两个电压方程,即解之,得2-8 电路如题图2-8所示,试用结点电压法计算图中电阻R L两端电压U,并计算理想电流源的功率。
解:由于计算负载电阻R L的电压U,与理想电流源串联的4Ω电阻和与理想电压源并联的8Ω电阻的存在与否无关,因此,这两个电阻的作用可被忽略,如解题图17所示,那么然而,在计算理想电流源的功率时,理想电流源两端的电压值是由与之并联的外电路所确定,因此,与理想电流源串联的4Ω电阻的作用就不能被忽略。


3.3 两种电源模型的等效变换导学案电子专业考纲:理解电压源和电流源的概念,并掌握它们之间的等效变换。
一、电压源1、定义:为电路提供一定电压的电源。
如图(a )(a) (b)理想电压源:为电路提供恒定不变电压的电源。
如图(b)(教师帮助学生分析电压源和理想电压源为电路提供电压和电流的特点)二、电流源通常所说的电流源一般是指理想电流源,其基本特性是所发出的电流固定不变(I s )或是一定的时间函数i s (t ),但电流源的两端电压却与外电路有关。
实际电流源是含有一定内阻r S 的电流源。
三、两种实际电源模型之间的等效变换实际电源可用一个理想电压源E 和一个电阻r 0串联的电路模型表示,其输出电压U 与输出电流I 之间关系为U = E - r 0I实际电源也可用一个理想电流源I S 和一个电阻r S 并联的电路模型表示,其输出电压U 与输出电流I 之间关系为U = r S I S - r S I对外电路来说,实际电压源和实际电流源是相互等效的,等效变换条件是r 0 = r S , E = r S I S 或 I S = E /r 0四、电源之间的等效变换注意事项:① 。
② 。
③ 。
④ 。
⑤ 。
【课前练习】一、判断题1、对外电路来说,一个有源二端网络可以用一个电压源来等效替代。
( )2、如果网络具有两个引出端与外电路相连不管其内部结构如何这样的网络就叫做二端网络。
( )3、理想电压源只是从电路中抽象出来的一种理想元件,实际上并不存在。
( )二、选择题1、如图1所示电路中,电流I值为 ( )A.2A B.-2 A C.4A D.-4A2、如图2所示电路中,电阻R2减小时,电流I将( )A.增大 B.减小 C.不变 D.不能确定3、如图3所示电路中的电压U为()A.2.5V;B.5V;C.7.5V;D.10V图1 图2 图3三、填空题1、如图4所示电路中,电流I= A,电阻消耗功率为,电流源的功率为,电压源的功率为。



1.5电压源和电流源的等效变换实际使用的电源,按其外特性,可分为电压源和电流源。
当一个电压源和一个电流源能够为同一个负载提供相同的电压、电流和功率时,这两个电源对该负载来说是等效的,可以互相置换,这种置换称为等效变换。
下面来讨论电压源和电流源的等效变换。
1.5.1 电压源在电路分析课程中,将能够向外电路提供电压的器件称为电压源。
如,电池,发电机等均是电压源。
在物理学中,电池表示成电动势E和内阻R相串联的电路模型,电池是一个典型的电压源,所以,电压源也可表示成电动势和内阻相串联的电路模型。
为了利用KVL的方便,对电压源特性进行标定时,通常不使用电动势E,而改用电压源所能输出的恒压值US,如图1-30(a)所示虚线框内部的电路。
图中电压源旁的箭头为US的参考方向。
注意: US 和E是不同性质的两个物理量,US是描述电压源所能输出的恒值电压,该值的大小与E相等,设定的参考方向与E相反。
当电压源与负载电阻RL相连时,根据KVL可得描述电压源外特性的函数式。
描述理想化电压源外特性的函数式是(1-57)由式1-57可见,理想化电压源的外特性曲线是直线,如图1-30(b)所示,图1-30(b)又称为电压源伏(U)-安(A)特性曲线。
图1-30(b)纵轴上的点,为电压源输出电流等于0的情况,相当于电压源处在开路的状态下。
当电压源开路时,电压源的输出电压U就等于US ,所以,US的值等于电压源的开路电压。
图1=30(b)横轴上的点,为电压源输出电压等于0的情况,相当于电压源处在短路的状态下(实际上这是不允许的),电压源输出电流为IS ,所以,IS称为短路电流。
计算短路电流的表达式为(1-58)U=f(I)曲线的斜率为R0,R越小,斜率越小,直线越平坦。
当R=0时,电源外特性曲线是一条平行与I轴的直线。
具有这种外特性曲线的电压源输出电压保持恒定值US,这种电压源称为理想电压源,简称恒压源。
将图1-30(a)虚线框内部电路的电阻R去掉,剩下的电路就是恒压源电路的模型。

电压源与电流源是电路中常见的两种基本元件,它们分别以恒定的电压和恒定的电流来驱动电路。
在电路分析和设计中,经常需要将电压源转换为等效的电流源,或将电流源转换为等效的电压源,以便更方便地进行电路分析和计算。
下面将分别介绍电压源与电流源的等效变换方法。
一、将电压源转换为等效的电流源1. 理论基础电压源的等效电流源转换是基于欧姆定律进行的。
根据欧姆定律,电流等于电压除以电阻,即I=V/R。
我们可以将电压源转换为等效的电流源,通过在电压源的正负端并联一个等效电阻,使得该电阻上的电流等于电压源的电压除以电阻值。
2. 转换公式电压源转换为等效电流源的公式为:I=V/R,其中I为等效电流源的输出电流,V为电压源的电压,R为等效电流源的电阻。
3. 举例说明假设有一个5V的电压源,需要将其转换为等效的电流源。
如果我们希望等效电流源的输出电流为1A,那么根据公式I=V/R,可得等效电阻R=V/I=5Ω。
我们可以在电压源的正负端并联一个5Ω的电阻,即可将电压源转换为等效的电流源。
二、将电流源转换为等效的电压源1. 理论基础电流源的等效电压源转换同样是基于欧姆定律进行的。
根据欧姆定律,电压等于电流乘以电阻,即V=IR。
我们可以将电流源转换为等效的电压源,通过在电流源的两端串联一个等效电压源,使得该电压等于电流源的电流乘以电阻值。
2. 转换公式电流源转换为等效电压源的公式为:V=IR,其中V为等效电压源的输出电压,I为电流源的电流,R为等效电压源的电阻。
3. 举例说明假设有一个2A的电流源,需要将其转换为等效的电压源。
如果我们希望等效电压源的输出电压为10V,那么根据公式V=IR,可得等效电阻R=V/I=5Ω。
我们可以在电流源的两端串联一个10V的电压源,并在其正负端串联一个5Ω的电阻,即可将电流源转换为等效的电压源。
电压源与电流源的等效变换方法可以在电路分析和设计中起到重要的作用。
通过合理应用这些方法,可以使得电路分析更加简便和直观,为电路设计提供重要的参考依据。
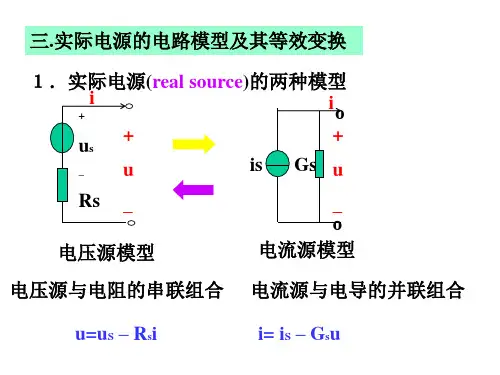
实际电压源与电流源的两种模型及其等效变换 - 电工基础1.实际电压源一个实际电压源,可用一个抱负电压源 us 与一个电阻 Rs 串联的支路模型来表征其特性。
当它向外电路供应电流时,它的端电压 u 总是小于 us ,电流越大端电压 u 越小。
us = Us时,其外特性曲线如下:Rs :电源内阻,一般很小。
2.实际电流源一个实际电流源,可用一个电流为 iS 的抱负电流源和一个内电导 GS 并联的模型来表征其特性。
当它向外电路供应电流时,并不是全部流出,其中一部分将在内部流淌,随着端电压的增加,输出电流减小。
Gs:电源内电导,一般很小。
iS = IS时,其外特性曲线如下:3.两种实际电源的等效互换实际电压源、实际电流源两种模型可以进行等效变换,所谓的等效是指端口的电压、电流在转换过程中保持不变。
即:通过比较,得等效的条件:留意事项(1)“等效”是指“对外”等效(等效互换前后对外伏—安特性全都),对内不等效。
开路的电压源中无电流流过 RS;开路的电流源可以有电流流过并联电导GS 。
电压源短路时,电阻RS有电流;电流源短路时,并联电导GS中无电流。
(2)留意转换前后US与IS的方向。
(3)进行电路分析和的计算时,恒压源(或受控电压源)串联电阻的支路和恒流源(或受控电流源)并联电阻的支路之间均可等效变换。
其中RS不肯定是电源内阻。
(4)抱负电压源和抱负电流源之间不能等效互换。
应用:利用电源转换可以简化电路计算。
例7.例8.受控源间的等效变换与独立电源相同可以用两种受控电源等效互换的方法简化受控源电路。
但简化时留意不能把把握量化简掉。
否则会留下一个没有把握量的受控源电路,使电路无法求解。
电源的两种模型及其等效变换
一个实际的直流电源(如直流发电机、蓄电池等)可以抽象成两种模型:
一种由独立电压源与线性时不变电阻元件串联而成;另一种由独立电流源与线性时不变电导并联而成。
在前一种电源模型中,电阻元件的电阻R称为原电源的内电阻,电压源的电压Us等于原电源的开路电压;在后一种电源模型中,线性时不变电阻元件的电导G称为原电源的内电导,电流源的电流Is等于原电源的短路电流。
由于它们代表同一个实际电源而有相同的外特性,所以它们能够等效互换。
两种模型等效互换的条件为Us和Is在电路计算中,为了计算方便,有时需要把一种电源模型变换成另一种电源模型。
把电压源模型换成电流源模型时,后者的电流源电流Is 必须等于Us,内电导必须等于电阻的倒数;反之亦然。
电源等效变换的条件随着电子技术的发展,电子设备的种类越来越丰富,而这些设备所需的电源也各不相同。
在实际应用中,往往需要将一个电源转换成另一个电源,以满足设备的需求。
这就需要进行电源等效变换。
本文将介绍电源等效变换的条件。
一、电源等效变换的定义电源等效变换是指将一个电源转换成另一个电源的过程。
在电源等效变换中,保持电路的输入输出特性不变,只改变电源的类型和参数。
电源等效变换可以分为两种类型:线性变换和非线性变换。
线性变换是指电源的变化与电路的输入输出关系成比例,非线性变换则不成比例。
二、电源等效变换的条件1. 等效电压在电源等效变换中,等效电压是指将原电源的电压转换成等效电压,使得在电路的输入端口处,原电源和等效电源的输出电压相同。
等效电压的计算公式如下:Ve = V1 × (R1 + R2) / R1其中,Ve为等效电压,V1为原电源的电压,R1为原电源的内阻,R2为电路的输入端口电阻。
2. 等效电流在电源等效变换中,等效电流是指将原电源的电流转换成等效电流,使得在电路的输入端口处,原电源和等效电源的输出电流相同。
等效电流的计算公式如下:Ie = V1 / (R1 + R2)其中,Ie为等效电流,V1为原电源的电压,R1为原电源的内阻,R2为电路的输入端口电阻。
3. 等效电阻在电源等效变换中,等效电阻是指将原电源的内阻转换成等效电阻,使得在电路的输入端口处,原电源和等效电源的输出电阻相同。
等效电阻的计算公式如下:Re = R1 × (R2 + Rl) / (R1 + R2)其中,Re为等效电阻,R1为原电源的内阻,R2为电路的输入端口电阻,Rl为电路的负载电阻。
4. 等效功率在电源等效变换中,等效功率是指将原电源的功率转换成等效功率,使得在电路的输入端口处,原电源和等效电源的输出功率相同。
等效功率的计算公式如下:Pe = V1^2 / (4R1)其中,Pe为等效功率,V1为原电源的电压,R1为原电源的内阻。
电压源与电流源的等效变换实验报告总结电压源与电流源的等效变换实验报告总结电压源与电流源的等效变换实验报告总结篇一:实验一电压源与电流源的等效变换实验一电压源与电流源的等效变换学号: 132021520 姓名:XXX 班级:13通信X班指导老师:X老师实验组号:5 实验地点:1实203 实验日期:201X年5月18日一、实验目的和要求:1(掌握电源外特性的测试方法;2(验证电压源与电流源等效变换的条件。
二、实验仪器:一、可调直流稳压电源 1台二、直流恒流源 1台三、直流数字电压表 1只四、直流数字毫安表 1只五、电阻器 1个三、实验原理:1、一个直流稳压电源在一定的电流范围内,具有很小的内阻,故在实用中,常将它视为一个理想的电压源,即其输出电压不随负载电流而变,其外特性,即其伏安特性U=f(I)是一条平行于I轴的直线。
一个恒流源在使用中,在一定的电压范围内,可视为一个理想的电流源,即其输出电流不随负载的改变而改变。
2(一个实际的电压源(或电流源),其端电压(或输出电压)不可能不随负载而变,因它具有一定的内组值。
故在实验中,用一个小阻值的电阻(或大电阻)与稳压源(或恒流源)相串联(或并联)来模拟一个电压源(或电流源)的情况。
3(一个实际的电源,就其外部特性而言,既可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个理想的电压源ES与一个电导g相并联的组合来表示,若它们向同样大小的负载供出同样大小的电流和端电压,则称这两个电源是等效的,即具有相同的外特性。
一个电压源与一个电流源等效变换条件为第 1 页共 4 页Is? 或 Es1 g= RR Es? 如下图6-1所示:Is1 R= g0g0四、实验内容:1(测定电压源的外特性(1)按图6-2(a)接线,ES为+6V直流稳压电源,调节R,令其阻值由大至小变化,记录两表的读数图6-2(a) 图6-2(b)(2)按图6-2(b)接线,虚线框可模拟为一个实际的电压源,调节R阻值,记录两表读数。