第四章机械振动(XXXX11改编)
- 格式:pptx
- 大小:1.61 MB
- 文档页数:54


机械振动的概念机械振动是指物体在受到外力作用下发生的周期性运动。
它是一种复杂的物理现象,在工程学、物理学、数学等领域都有广泛的应用。
机械振动的研究对于解决工程问题、提高设备性能以及深入理解物体的运动规律具有重要意义。
首先,我们可以通过观察一个简单的机械振动现象来了解它的概念。
假设有一个质量为m的物体,它通过一个弹簧与固定点相连接。
当这个物体受到外力作用时,它会相对于平衡位置发生振动。
这种振动可以是正弦函数的形式,也可以是其他复杂的波形。
物体在振动过程中,会在振幅达到最大值时向一个方向运动,然后在振幅达到最小值时向另一个方向运动。
这种周期性的运动就是机械振动。
机械振动的重要性在于它的广泛应用。
在机械工程中,振动是一个常见的问题。
例如,汽车发动机的不平衡力会导致汽车振动,影响乘坐舒适性和发动机寿命;建筑物受到地震或风力的作用时,也会发生振动,这需要对建筑物结构做出相应的设计和补强;在电子设备中,电动机的振动会影响设备的稳定性和寿命等等。
因此,了解和掌握机械振动的特性和原理,对于解决这些问题具有至关重要的意义。
对于机械振动的研究,主要包括振动的频率、振幅、相位和周期等几个基本概念。
振动的频率是指单位时间内振动的次数。
频率用赫兹(Hz)来表示,1 Hz代表1秒内振动一次。
振动的频率取决于物体的质量和弹性特性。
例如,弹簧的刚度越大,物体的频率越高;物体的质量越大,频率越低。
频率是描述振动特征的重要参数,它能够帮助我们了解物体的振动情况和特性。
振动的振幅是指物体运动的最大偏离量。
它表示了振动的强度,振幅越大,振动的能量也就越大。
振动的振幅可以通过测量物体相对于平衡位置的位置来确定。
例如,对于一个简单的弹簧振子,可以通过测量振子达到的最大位移来确定振幅。
振幅的大小对于振动的影响很大,它不仅决定了物体的振动幅度,还会影响到物体的能耗、寿命等。
因此,在设计和使用振动设备时,需要注意控制振动的振幅。
振动的相位是指物体在振动中的位置关系。


机械振动机械波机械振动和机械波是物理学中重要的概念,涉及到了物体的振动和波动特性。
机械振动是指物体或系统在受到外界力的作用下发生的周期性或非周期性的振动运动,而机械波是指机械振动在介质中传播的能量传递过程。
机械振动有两个重要的参数,即振动周期和振幅。
振动周期是指一个完整的振动循环所需要的时间,通常用秒(s)表示。
振幅则是指振动的最大位移或最大速度,通常用米(m)来表示。
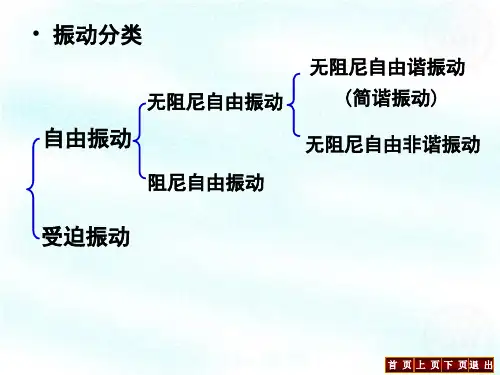
机械振动分为简谐振动和非简谐振动两种。
简谐振动是指当物体受到恢复力的作用后,其振动状态可以通过正弦或余弦函数来描述。
而非简谐振动则是指物体受到的恢复力不满足线性关系,振动状态无法通过简单的正弦或余弦函数来描述。
机械振动的运动可以通过振动方程来描述。
对于简谐振动而言,振动方程可以表示为x(t) = A * sin(ωt + φ),其中x(t)是物体的位移,A是振幅,ω是角频率,t是时间,φ是相位差。
振动方程可以描述物体振动的位移、速度和加速度的关系,从而提供了对振动状态的全面了解。
机械波是机械振动在介质中传播的能量传递过程。
波动是由于介质中某一点的振动引起附近点的振动,从而传递能量。
机械波有两种主要类型,即横波和纵波。
横波是指波动的振动方向垂直于能量传播方向的波动,例如水波。
纵波则是指波动的振动方向与能量传播方向一致的波动,例如声波。
机械波的传播速度可以通过介质的性质和条件来确定。
对于弹性介质而言,传播速度可以表示为v = √(E/ρ),其中v是波速,E是介质的杨氏模量,ρ是介质的密度。
不同介质的波速是不同的,比如在空气中,声速大约为343m/s,而在水中,水波的波速则约为1480m/s。
机械波的特性还包括波长和频率。
波长是指相邻两个振动峰或波谷之间的距离,通常用λ表示,单位是米。
频率是指在单位时间内波动中的相邻振动周期的个数,通常用赫兹(Hz)表示。
波长和频率之间有一个简单的关系,即v = λ * f,其中v是波速,λ是波长,f 是频率。




机械振动的概念精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】第一章绪论1-1 机械振动的概念振动是一种特殊形式的运动,它是指物体在其平衡位置附近所做的往复运动。
如果振动物体是机械零件、部件、整个机器或机械结构,这种运动称为机械振动。
振动在大多数情况下是有害的。
由于振动,影响了仪器设备的工作性能;降低了机械加工的精度和粗糙度;机器在使用中承受交变载荷而导致构件的疲劳和磨损,以至破坏。
此外,由于振动而产生的环境噪声形成令人厌恶的公害,交通运载工具的振动恶化了乘载条件,这些都直接影响了人体的健康等等。
但机械振动也有可利用的一面,在很多工艺过程中,随着不同的工艺要求,出现了各种类型利用振动原理工作的机械设备,被用来完成各种工艺过程,如振动输送、振动筛选、振动研磨、振动抛光、振动沉桩等等。
这些都在生产实践中为改善劳动条件、提高劳动生产率等方面发挥了积极作用。
研究机械振动的目的就是要研究产生振动的原因和它的运动规律,振动对机器及人体的影响,进而防止与限制其危害,同时发挥其有益作用。
任何机器或结构物,由于具有弹性与质量,都可能发生振动。
研究振动问题时,通常把振动的机械或结构称为振动系统(简称振系)。
实际的振系往往是复杂的,影响振动的因素较多。
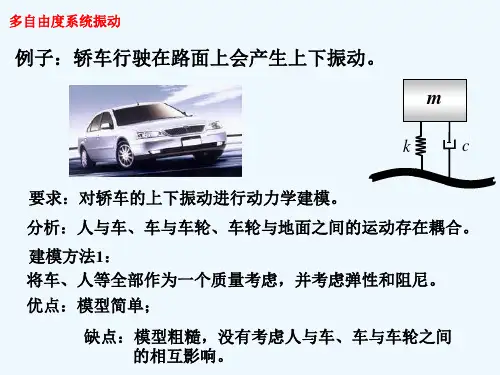
为了便于分析研究,根据问题的实际情况抓住主要因素,略去次要因素,将复杂的振系简化为一个力学模型,针对力学模型来处理问题。
振系的模型可分为两大类:离散系统(或称集中参数系统)与连续系统(或称分布参数系统),离散系统是由集中参数元件组成的,基本的集中参数元件有三种:质量、弹簧与阻尼器。
其中质量(包括转动惯量)只具有惯性;弹簧只具有弹性,其本身质量略去不计,弹性力只与变形的一次方成正比的弹簧称为线性弹簧;在振动问题中,各种阻力统称阻尼,阻尼器既不具有惯性,也不具有弹性,它是耗能元件,在有相对运动时产生阻力,其阻力与相对速度的一次方成正比的阻尼器称为线性阻尼器。
机械振动公式范文机械振动是指物体在一定时间内围绕平衡位置作周期性的往复运动,通常由弹簧系统和质量块构成。
机械振动公式是描述机械振动运动规律的数学表达式。
下面将介绍几个常见的机械振动公式。
1.简谐振动公式:简谐振动是指物体在外力作用下,其振幅、频率和周期都保持不变的振动。
在简谐振动中,振动物体的位置随时间的变化符合正弦函数的规律。
假设物体的简谐振动方程为:x = A * sin(ωt + φ)其中,x为物体的位移,A为振幅,ω为角频率,t为时间,φ为相位差。
2.频率和周期的关系:频率是指在单位时间内振动的次数,周期是指完成一次完整振动所需要的时间。
频率和周期之间满足以下关系:f=1/T其中,f为频率,T为周期。
3.动力学公式:物体在振动过程中会受到外力的作用,根据牛顿第二定律可以得到物体振动的动力学方程。
F=m*a其中,F为受力,m为物体的质量,a为加速度,根据振动的定义,加速度可以表示为速度对时间的导数,速度可以表示为位移对时间的导数:a = d²x/dt²将以上两个公式代入动力学方程中,可以得到:m * d²x/dt² = -k * x其中,k为弹簧的劲度系数,x为物体的位移。
4.振动的频率:根据动力学方程可以推导出振动的频率公式。
以弹簧振子为例,假设弹簧的劲度系数为k,质量为m,则振动的频率可以表示为:ω=√(k/m)其中,ω为角频率。
5.振动的周期:振动的周期可以用频率的倒数表示:T=1/f结合振动的频率公式可以得到:T=2π√(m/k)其中,T为周期。
上述是机械振动中的几个常见公式,这些公式为研究振动现象和解决振动问题提供了重要的数学工具。
在实际应用中,可以根据不同的振动系统和条件,选择适用的公式来描述和计算机械振动。