二项分布方差公式推导复习过程

二项分布、超几何分布数学期望与方差公式的推导高中教材中对二项分布和超几何分布数学期望与方差公式没有给出推导公式，现笔者给出一推导过程仅供参考。

预备公式一11--=k n k n nC kC （1≥n ），利用组合数计算公式即可证明。

预备公式二[]22)()()(ξξξE E D -=，证明过程可见教材。

预备公式三22)1()1(---=-k n k n C n n C k k （2,2≥≥k n ），利用组合数计算公式即可证明。

预备公式四),,,,(022110n k m k N k n m C C C C C C C C C kn m m k n k m n k m n k m n ≤≤∈=++++++-- ，利用恒等式m n n m x x x )1()1()1(++=++的二项展开式中k x 的系数相等可证。

一、二项分布在n 次独立重复试验中，每次试验中事件A 发生的概率为p （10<<p ），事件A 发生次数为ξ，则ξ的概率分布列为：二项分布的数学期望np p p np p pC np p p nC p p kC p p kC E n nk k n k k n nk kn k k n nk kn kk nnk kn kkn=+-=-=-=-=-=-=----=---=-=-∑∑∑∑1111111110)1()1()1()1()1()(ξ2.二项分布的方差[])1()1()1()1()1()1()1()()1()1()1()1()1()1()()1()()()(222222n2222222n22222n222n1n122n122n222p np p n np p p p n n p n np p p Cp n n p n np p p C n n p n E p p C k k p n p p kC p p C k k p n p p C k np p p C k E E D n k k n k k n k k n k k n k kn kknk k n kk n k kn kknk k n kk n k kn kk n-=-++--=-+--=-+--=-+--=--+--=--=--=-=-=----=---=-=-=-=-=-∑∑∑∑∑∑∑ξξξξ二、超几何分布一批产品共N 件，其中有M 件不合格品，N -M 件合格品，从中随机取出n 件产品中，不合格品数X 的概率分布列为：其中（，）。

第十讲二项分布及应用随机变量均值与方差知识要点1.事件相互独立性(概率乘法公式)设A、B为两个事件，如果P(AB)＝P(A)P(B)，那么称事件A与事件B相互独立．2. 互斥事件概率加法公式：如果事件A与事件B互斥，那么P(A＋B)＝P(A)＋P(B)．3.对立事件概率：假设事件A与事件B互为对立事件，那么P(A)＝1－P(B)．4.条件概率加法公式：假设B、C是两个互斥事件，那么P(B∪C|A)＝P(B|A)＋P(C|A)5.独立重复试验：在一样条件下重复做n次试验称为n次独立重复试验，即假设用A i(i＝1,2，…，n)表示第i次试验结果，那么P(A1A2A3…A n)＝P(A1)P(A2)P(A3)…P(A n)．注：判断某事件发生是否是独立重复试验，关键有两点(1)在同样条件下重复，相互独立进展；(2)试验结果要么发生，要么不发生．6.二项分布：在n次独立重复试验中，设事件A发生次数为X，在每次试验中事件A发生概率为p，那么在n次独立重复试验中，事件A恰好发生k 次概率为P(X＝k)＝C k n p k·(1－p)n－k(k＝0,1,2，…，n)，此时称随机变量X 服从二项分布，记作X～B(n，p)，并称p为成功概率．注：判断一个随机变量是否服从二项分布，要看两点(1)是否为n次独立重复试验．(2)随机变量是否为在这n次独立重复试验中某事件发生次数．7.离散型随机变量均值与方差及其性质定义：假设离散型随机变量X分布列为P(ξ＝x i)＝p i，i＝1,2，…，n.(1)均值：称E(X)＝x1p1＋x2p2＋…＋x i p i＋…＋x n p n为随机变量X均值或数学期望．n(x i－E(X))2p i为随机变量X方差，其算术平方根(2)方差：D(X)＝∑i＝1D X为随机变量X标准差．(3)均值与方差性质：(1)E(aX＋b)＝aE(X)＋b；(2)D(aX＋b)＝a2D(X)．(a，b为常数)8.两点分布与二项分布均值、方差变量X服从两点分布：E(X)＝p，D(X)＝p(1－p)；X～B(n，p)： E(X)＝np ，D(X)＝np(1－p)典例精析例1.【2021 高考四川，理17】某市A,B两所中学学生组队参加辩论赛，A 中学推荐3名男生，2名女生，B中学推荐了3名男生，4名女生，两校推荐学生一起参加集训，由于集训后队员水平相当，从参加集训男生中随机抽取3人，女生中随机抽取3人组成代表队〔1〕求A中学至少有1名学生入选代表队概率.〔2〕某场比赛前，从代表队6名队员中随机抽取4人参赛，设X表示参赛男生人数，求X得分布列与数学期望.例2．如图，用K、A1、A2三类不同元件连接成一个系统．当K正常工作且A1、A2至少有一个正常工作时，系统正常工作．K、A1、A2正常工作概率依次为0.9、0.8、0.8，那么系统正常工作概率为 ( )A．0.960 C．0.720例3.(2021·山东高考)甲、乙两支排球队进展比赛，约定先胜3局者获得比赛胜利，比赛随即完毕．除第五局甲队获胜概率是12外，其余每局比赛甲队获胜概率都是23，假设各局比赛结果相互独立．(1)分别求甲队以3∶0,3∶1,3∶2胜利概率．(2)假设比赛结果为3∶0或3∶1，那么胜利方得3分，对方得0分；假设比赛结果为3∶2，那么胜利方得2分，对方得1分．求乙队得分X分布列及数学期望．例4.为贯彻“激情工作，快乐生活〞理念，某单位在工作之余举行趣味知识有奖竞赛，比赛分初赛与决赛两局部，为了增加节目趣味性，初赛采用选手选一题答一题方式进展，每位选手最多有5次选答题时机，选手累计答对3题或答错3题即终止其初赛比赛，答对3题者直接进入决赛，答错3题者那么被淘汰，选手甲答题正确率为2 3 .(1)求选手甲答题次数不超过4次可进入决赛概率；(2)设选手甲在初赛中答题个数ξ，试写出ξ分布列，并求ξ数学期望．例5.(2021·福建高考改编)为回馈顾客，某商场拟通过摸球兑奖方式对1 000位顾客进展奖励，规定：每位顾客从一个装有4个标有面值球袋中一次性随机摸出2个球，球上所标面值之与为该顾客所获奖励额．(1)假设袋中所装4个球中有1个所标面值为50元，其余3个均为10元．求：①顾客所获奖励额为60元概率；②顾客所获奖励额分布列及数学期望．(2)商场对奖励总额预算是60 000元，为了使顾客得到奖励总额尽可能符合商场预算且每位顾客所获奖励额相对均衡．下面给出两种方案：方案1：4个球中所标面值分别为10元，10元，50元，50元；方案2：4个球中所标面值分别为20元，20元，40元，40元．如果你作为商场经理，更倾向选择哪种方案？例6．(13分)如下图，是某城市通过抽样得到居民某年月均用水量(单位：吨)频率分布直方图．(1)求直方图中x值；(2)假设将频率视为概率，从这个城市随机抽取3位居民(看作有放回抽样)，求月均用水量在3至4吨居民数X分布列、数学期望与方差．例7．(12分)某网站用“10分制〞调查一社区人们幸福度．现从调查人群中随机抽取16名，以下茎叶图记录了他们幸福度分数(以小数点前一位数字为茎，小数点后一位数字为叶)：(1)指出这组数据众数与中位数；(2)假设幸福度不低于9，那么称该人幸福度为“极幸福〞．求从这16人中随机选取3人，至多有1人是“极幸福〞概率；(3)以这16人样本数据来估计整个社区总体数据，假设从该社区(人数很多)任选3人，记ξ表示抽到“极幸福〞人数，求ξ分布列及数学期望．例8.【2021 高考湖南，理18】某商场举行有奖促销活动，顾客购置一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球甲箱与装有5个红球、5个白球乙箱中，各随机摸出1个球，在摸出2个球中，假设都是红球，那么获一等奖；假设只有1个红球，那么获二等奖；假设没有红球，那么不获奖.〔1〕求顾客抽奖1次能获奖概率；〔2〕假设某顾客有3次抽奖时机，记该顾客在3次抽奖中获一等奖次数为X，求X分布列与数学期望.例9.〔2021 河北张家口市 三模21〕〔本小题总分值12分〕 设函数()21x f x e x ax ＝－－－． (Ⅰ)假设0a ＝，求()f x 单调区间；(Ⅱ)假设当0x ≥时，()0f x ≥，求a 取值范围． 参考答案例1.【2021 高考四川，理17】某市A,B 两所中学学生组队参加辩论赛，A 中学推荐3名男生，2名女生，B 中学推荐了3名男生，4名女生，两校推荐学生一起参加集训，由于集训后队员水平相当，从参加集训男生中随机抽取3人，女生中随机抽取3人组成代表队 〔1〕求A 中学至少有1名学生入选代表队概率.〔2〕某场比赛前，从代表队6名队员中随机抽取4人参赛，设X 表示参赛男生人数，求X 得分布列与数学期望.【答案】〔1〕A 中学至少1名学生入选概率为99100p =. 〔2〕X 分布列为：X 期望为()2E X =.【解析】〔1〕由题意，参加集训男女生各有6名.参赛学生全从B 中抽取〔等价于A 中没有学生入选代表队〕概率为333433661100C C C C =.因此，A 中学至少1名学生入选概率为1991100100-=. 〔2〕根据题意，X 可能取值为1，2，3. 所以X 分布列为：因此，X 期望为131()1232555E X =⨯+⨯+⨯=.例2．如图10－8－1，用K 、A 1、A 2三类不同元件连接成一个系统．当K 正常工作且A 1、A 2至少有一个正常工作时，系统正常工作．K 、A 1、A 2正常工作概率依次为、、，那么系统正常工作概率为( B )A ．0.960B ．C ．0.720D ．【答案】 B 12A A 、 至少有一个正常工作概率为21(10.8)0.96P =--= ，那么系统正常工作概率为0.90.960.864K P P ⋅=⨯=例3.(2021·山东高考)甲、乙两支排球队进展比赛，约定先胜3局者获得比赛胜利，比赛随即完毕．除第五局甲队获胜概率是12外，其余每局比赛甲队获胜概率都是23，假设各局比赛结果相互独立．(1)分别求甲队以3∶0,3∶1,3∶2胜利概率．(2)假设比赛结果为3∶0或3∶1，那么胜利方得3分，对方得0分；假设比赛结果为3∶2，那么胜利方得2分，对方得1分．求乙队得分X 分布列及数学期望．【尝试解答】 (1)记“甲队以3∶0胜利〞为事件A 1，“甲队以3∶1胜利〞为事件A 2，“甲队以3∶2胜利〞为事件A 3，由题意，各局比赛结果相互独立， 故P (A 1)＝⎝ ⎛⎭⎪⎪⎫233＝827，P (A 2)＝C 23⎝ ⎛⎭⎪⎪⎫232⎝ ⎛⎭⎪⎪⎫1－23×23＝827，P (A 3)＝C 24⎝ ⎛⎭⎪⎪⎫232⎝ ⎛⎭⎪⎪⎫1－232×12＝427. 所以甲队以3∶0胜利，以3∶1胜利概率都为827，以3∶2胜利概率为427. (2)设“乙队以3∶2胜利〞为事件A 4，由题意，各局比赛结果相互独立，所以P (A 4)＝C 24⎝⎛⎭⎪⎪⎫1－232⎝ ⎛⎭⎪⎪⎫232×⎝ ⎛⎭⎪⎪⎫1－12＝427.由题意，随机变量X 所有可能取值为0,1,2,3， 根据事件互斥性得P (X ＝0)＝P (A 1＋A 2)＝P (A 1)＋P (A 2)＝1627.又P (X ＝1)＝P (A 3)＝427，P (X ＝2)＝P (A 4)＝427，P (X ＝3)＝1－P (X ＝0)－P (X ＝1)－P (X ＝2)＝327，故X 分布列为所以EX ＝0×27＋1×27＋2×27＋3×27＝9.例4.为贯彻“激情工作，快乐生活〞理念，某单位在工作之余举行趣味知识有奖竞赛，比赛分初赛与决赛两局部，为了增加节目趣味性，初赛采用选手选一题答一题方式进展，每位选手最多有5次选答题时机，选手累计答对3题或答错3题即终止其初赛比赛，答对3题者直接进入决赛，答错3题者那么被淘汰，选手甲答题正确率为23.(1)求选手甲答题次数不超过4次可进入决赛概率；(2)设选手甲在初赛 中答题个数ξ，试写出ξ分布列，并求ξ数学期望．【尝试解答】 (1)选手甲答3道题进入决赛概率为⎝ ⎛⎭⎪⎪⎫233＝827，选手甲答4道题进入决赛概率为C23·⎝ ⎛⎭⎪⎪⎫232·13·23＝827，∴选手甲答题次数不超过4次可进入决赛概率P ＝827＋827＝1627；(2)依题意，ξ可取取值为3、4、5，那么有P (ξ＝3)＝⎝ ⎛⎭⎪⎪⎫233＋⎝ ⎛⎭⎪⎪⎫133＝13，P (ξ＝4)＝C23·⎝ ⎛⎭⎪⎪⎫232·13·23＋C 23·⎝ ⎛⎭⎪⎪⎫132·23·13＝1027，P (ξ＝5)＝C 24·⎝ ⎛⎭⎪⎪⎫232·⎝ ⎛⎭⎪⎪⎫132·23＋C 24·⎝ ⎛⎭⎪⎪⎫232·⎝ ⎛⎭⎪⎪⎫132·13＝827， 因此，有∴Eξ＝3×3＋4×27＋5×27＝27.规律方法2 求离散型随机变量均值与方差方法：(1)先求随机变量分布列，然后利用均值与方差定义求解．(2)假设随机变量X ～B (n ，p )，那么可直接使用公式E (X )＝np ，D (X )＝np (1－p )求解．例5.(2021·福建高考改编)为回馈顾客，某商场拟通过摸球兑奖方式对1 000位顾客进展奖励，规定：每位顾客从一个装有4个标有面值球袋中一次性随机摸出2个球，球上所标面值之与为该顾客所获奖励额． (1)假设袋中所装4个球中有1个所标面值为50元，其余3个均为10元．求：①顾客所获奖励额为60元概率；②顾客所获奖励额分布列及数学期望．(2)商场对奖励总额预算是60 000元，为了使顾客得到奖励总额尽可能符合商场预算且每位顾客所获奖励额相对均衡．下面给出两种方案：方案1：4个球中所标面值分别为10元，10元，50元，50元；方案2：4个球中所标面值分别为20元，20元，40元，40元． 如果你作为商场经理，更倾向选择哪种方案？ 【解答】 (1)设顾客所获奖励额为X .①依题意，得P (X ＝60)＝C 11C 13C 24＝12，即顾客所获奖励额为60元概率为12. ②依题意，得X 所有可能取值为20,60.P (X ＝20)＝C 23C 24＝12，P (X ＝60)＝12， 即X 分布列为X 20 60 P1212所以顾客所获奖励额数学期望为E (X )＝20×12＋60×12＝40(元)．(2)对于方案1：设每位顾客获得奖励额为X 1元，那么随机变量X 1分布列为X 1 20 60 100 P162316∴数学期望E (X 1)＝20×16＋60×23＋100×16＝60，方差D (X 1)＝20－6026＋23×(60－60)2＋100－6026＝1 6003.对于方案2：设顾客获得奖励额为X 2元，那么X 2分布列为X 2 40 60 80 P162316∴数学期望E (X 2)＝40×16＋60×23＋80×16＝60，方差D (X 2)＝40－6026＋23×(60－60)2＋80－6026＝4003.根据预算，每个顾客平均奖励额为60元，且E (X 1)＝E (X 2)＝60，D (X 1)>D (X 2)．因此，根据商场设想，应选择方案2.例6.如图10－9－4所示，是某城市通过抽样得到居民某年月均用水量(单位：吨)频率分布直方图．图10－9－4(1)求直方图中x 值；(2)假设将频率视为概率，从这个城市随机抽取3位居民(看作有放回抽样)，求月均用水量在3至4吨居民数X 分布列、数学期望与方差． 【解】 (1)依题意及频率分布直方图知，0．02＋＋x ＋＋＝1，解得x ＝0.12.(2)由题意知，X ～B (3,0.1)．因此P (X ＝0)＝C 03×3＝，P (X ＝1)＝C 13××2＝，P (X ＝2)＝C 23×2×＝， P (X ＝3)＝C 33×3＝0.001.故随机变量X 分布列为X 0123PXX 方差为D (X )＝3××(1－0.1)＝0.27.例7．某网站用“10分制〞调查一社区人们幸福度．现从调查人群中随机抽取16名，以下茎叶图10－9－3记录了他们幸福度分数(以小数点前一位数字为茎，小数点后一位数字为叶)：图10－9－3(1)指出这组数据众数与中位数；(2)假设幸福度不低于9，那么称该人幸福度为“极幸福〞．求从这16人中随机选取3人，至多有1人是“极幸福〞概率；(3)以这16人样本数据来估计整个社区总体数据，假设从该社区(人数很多)任选3人，记ξ表示抽到“极幸福〞人数，求ξ分布列及数学期望．【解】 (1)众数：8,6；中位数：(2)由茎叶图可知，幸福度为“极幸福〞人有4人．设A i 表示所取3人中有i 个人是“极幸福〞，至多有1人是“极幸福〞记为事件A ，那么P (A )＝P (A 0)＋P (A 1)＝C 312C 316＋C 14C 212C 316＝121140(3)从16人样本数据中任意选取1人，抽到“极幸福〞人概率为416＝14，故依题意可知，从该社区中任选1人，抽到“极幸福〞人概率P ＝14ξ可能取值为0,1,2,3P (ξ＝0)＝⎝ ⎛⎭⎪⎪⎫343＝2764；P (ξ＝1)＝C 1314⎝ ⎛⎭⎪⎪⎫342＝2764P (ξ＝2)＝C23⎝⎛⎭⎪⎪⎫14234＝964；P (ξ＝3)＝⎝ ⎛⎭⎪⎪⎫143＝164 所以ξ分布列为Eξ＝0×64＋1×64＋2×64＋3×64＝另解由题可知ξ～B ⎝⎛⎭⎪⎪⎫3，14，所以Eξ＝3×14＝0.75.例8. 【2021 高考湖南，理18】某商场举行有奖促销活动，顾客购置一定金额商品后即可抽奖，每次抽奖都从装有4个红球、6个白球甲箱与装有5个红球、5个白球乙箱中，各随机摸出1个球，在摸出2个球中，假设都是红球，那么获一等奖；假设只有1个红球，那么获二等奖；假设没有红球，那么不获奖.〔1〕求顾客抽奖1次能获奖概率；〔2〕假设某顾客有3次抽奖时机，记该顾客在3次抽奖中获一等奖次数为X ，求X 分布列与数学期望.【答案】〔1〕107；〔2〕详见解析. 【解析】试题分析：〔1〕记事件1A =｛从甲箱中摸出1个球是红球｝，2A =｛从乙箱中摸出1个球是红球｝1B =｛顾客抽奖1次获一等奖｝，2B =｛顾客抽奖1次获二等奖｝，C =｛顾客抽奖1次能获奖｝，那么可知1A 与2A 相互独立，12A A 与12A A 互斥，1B 与2B 互斥，且1B =12A A ，2B =12A A +12A A ，12C B B =+，再利用概率加法公式即可求解；〔2〕分析题意可知1(3,)5XB ，分别求得00331464(0)()()55125P XC ===，11231448(1)()()55125P X C ===，22131412(2)()()55125P X C ===，3303141(3)()()55125P X C ===，即可知X概率分布及其期望.试题解析：〔1〕记事件1A =｛从甲箱中摸出1个球是红球｝，2A =｛从乙箱中摸出1个球是红球｝1B =｛顾客抽奖1次获一等奖｝，2B =｛顾客抽奖1次获二等奖｝，C =｛顾客抽奖1次能获奖｝，由题意，1A 与2A 相互独立，12A A 与12A A 互斥，1B 与2B 互斥，且1B =12A A ，2B =12A A +12A A ，12C B B =+，∵142()105P A ==，251()102P A ==，∴11212211()()()()525P B P A A P A P A ===⨯=， 21211(1)(1)52522=⨯-+-⨯=，故所求概率为1212117()()()()5210P C P B B P B P B =+=+=+=； 〔2〕 顾【考点定位】1.概率加法公式；2.离散型随机变量概率分布与期望. 【名师点睛】此题主要考察了离散型随机变量概率分布与期望以及概率统计在生活中实际应用，这一直都是高考命题热点，试题背景由传统摸球，骰子问题向现实生活中热点问题转化，并且与统计联系越来越密切，与统计中抽样，频率分布直方图等根底知识综合试题逐渐增多，在复习时应予以 关注.例9.【2021 高考四川，理21】函数22()2()ln 22f x x a x x ax a a =-++--+，其中0a >.〔1〕设()g x 是()f x 导函数，评论()g x 单调性；〔2〕证明：存在(0,1)a ∈，使得()0f x ≥在区间∞(1,+)内恒成立，且()0f x =在∞(1,+)内有唯一解.【答案】〔1〕当104a <<时，()g x在区间)+∞上单调递增，在区间上单调递减；当14a ≥时，()g x 在区间(0,)+∞上单调递增.〔2〕详见解析.【解析】〔1〕由，函数()f x 定义域为(0,)+∞，()()222ln 2(1)a g x f x x a x x '==---+，所以222112()2()2224()2x a a g x x x x-+-'=-+=. 当104a <<时，()g x在区间)+∞上单调递增，在区间上单调递减； 当14a ≥时，()g x 在区间(0,)+∞上单调递增. 〔2〕由()222ln 2(1)0af x x a x x'=---+=，解得11ln 1x xa x ---=+.令2211111ln 1ln 1ln 1ln ()2()ln 2()2()1111x x x x x x x x x x x x x x x x xϕ------------=-++--+++++. 那么211(2)2(1)10,())2()011e e e e e eϕϕ----=>=--<++，.故存在0(1,)x e ∈，使得0()0x ϕ=.令00011ln ,()1ln (1)1x x a u x x x x x ---==--≥+，. 由1()10u x x'=-≥知，函数()u x 在区间(1,)+∞上单调递增. 所以001110()(1)()20111111u x u u e e a x e e----=<=<=<++++. 即0(0,1)a ∈.【考点定位】此题考察导数运算、导数在研究函数中应用、函数零点等根底知识，考察推理论证能力、运算求解能力、创新意识，考察函数与方程、数形结合、分类与整合，化归与转化等数学思想.【考点定位】此题考察导数运算、导数在研究函数中应用、函数零点等根底知识，考察推理论证能力、运算求解能力、创新意识，考察函数与方程、数形结合、分类与整合，化归与转化等数学思想.【名师点睛】此题作为压轴题，难度系数应在以下.导数与微积分作为大学重要内容，在中学要求学生掌握其根底知识，在高考题中也必有表达.一般地，只要掌握了课本知识，是完全可以解决第〔1〕题，所以对难度最大最后一个题，任何人都不能完全放弃，这里还有不少分是志在必得.解决函数题需要一个重要数学思想是数形结合，联系图形大胆猜测. 在此题中，结合待证结论，可以想象出()f x 大致图象，要使得()0f x ≥在区间∞(1,+)内恒成立，且()0f x =在∞(1,+)内有唯一解，那么这个解0x 应为极小值点，且极小值为0，当0(1,)x x ∈时，()f x 图象递减；当0(,)x x ∈+∞时，()f x 图象单调递增，顺着这个思想，便可找到解决方法.。

二项分布的期望和方差的详细证明二项分布是概率论中一种常见的离散概率分布，它描述了在重复进行n次独立的二值试验中成功的次数。

在二项分布中，每一次试验只有两个可能的结果，通常被称为成功和失败。

本文将详细证明二项分布的期望和方差。

1. 期望的证明设一个二项分布的随机变量X代表成功的次数，p代表每次试验成功的概率，n代表试验的总次数。

则X服从参数为n和p的二项分布。

首先，我们知道每次试验成功的概率为p，失败的概率为1-p。

因此，成功的次数X可以表示为X = X1 + X2 + ... + Xn，其中Xi表示第i次试验是否成功的指示变量。

对于每个指示变量Xi，根据期望的性质，有E(Xi) = 1 * P(Xi = 1) +0 * P(Xi = 0) = p。

由于每个试验都是独立的，所以期望具有线性性质，即E(X) =E(X1 + X2 + ... + Xn) = E(X1) + E(X2) + ... + E(Xn) = np。

因此，二项分布的期望为np。

2. 方差的证明方差是对随机变量的离散程度的度量。

在二项分布中，方差的计算需要用到方差的性质和协方差的概念。

首先，我们知道对于任意两个随机变量X和Y，它们的协方差定义为Cov(X, Y) = E((X - E(X))(Y - E(Y)))。

对于二项分布的随机变量X，我们可以找到另一个与X独立的随机变量Y，使得X + Y = n。

根据协方差的性质，Cov(X, Y) = 0。

在二项分布中，我们可以得到X和Y的方差之和为二项分布的方差，即Var(X + Y) = Var(n) = Var(X) + Var(Y) + 2Cov(X, Y)。

由于X和Y独立，所以协方差Cov(X, Y) = 0，上述方程变为Var(X + Y) = Var(X) + Var(Y)。

因此，Var(X) = Var(n) - Var(Y)。

根据二项分布的性质，Var(n) = np(1-p)。

二项分布的期望和方差的详细证明在概率论中，二项分布是一种非常重要的离散概率分布。

它描述了在 n 次独立重复的伯努利试验中，成功的次数 X 的概率分布。

在深入研究二项分布时，了解其期望和方差是至关重要的。

接下来，我们将详细证明二项分布的期望和方差。

首先，让我们明确二项分布的定义。

如果一个随机变量 X 服从参数为 n 和 p 的二项分布，记作 X ～ B(n, p)，其中 n 表示试验的次数，p 表示每次试验成功的概率。

那么，二项分布的概率质量函数为：P(X ＝ k) ＝ C(n, k) p^k （1 p)＾（n k) ，其中 k ＝ 0, 1, 2,， n ，C(n, k) 表示从 n 个元素中选取 k 个元素的组合数。

接下来，我们开始证明二项分布的期望。

期望（Expected Value），通常用 E(X) 表示，它反映了随机变量取值的平均水平。

我们有：E(X) ＝∑k ＝ 0 to n k P(X ＝ k)＝∑k ＝ 0 to n k C(n, k) p^k （1 p)＾（n k)为了计算这个和式，我们可以使用一些技巧。

首先，我们对 k C(n, k) 进行变形：k C(n, k) ＝ n C(n 1, k 1)将其代入期望的表达式中：E(X) ＝∑k ＝ 0 to n n C(n 1, k 1) p^k （1 p)＾（n k)令 j ＝ k 1 ，则 k ＝ j ＋ 1 ，当 k ＝ 0 时，j ＝－1 ；当 k ＝ n 时，j ＝ n 1 。

则上式可以改写为：E(X) ＝n ∑j ＝－1 to n 1 C(n 1, j) p^（j ＋ 1) （1 p)＾（（n 1) j)因为当 j ＝－1 时，C(n 1, －1) ＝ 0 ，所以可以将求和的下限改为0 。

E(X) ＝n p ∑j ＝ 0 to n 1 C(n 1, j) p^j （1 p)＾（（n 1) j)而∑j ＝ 0 to n 1 C(n 1, j) p^j （1 p)＾（（n 1) j) 恰好是二项分布B(n 1, p) 的所有概率之和，其值为 1 。

二项分布,超几何分布数学期望与方差公式的推导在概率论和数理统计中，二项分布和超几何分布是重要的概率分布，它们的数学期望与方差可以用一定的公式来表示，并可以通过推导来算出。

本文从实际问题出发，详细介绍了二项分布和超几何分布数学期望与方差公式的推导过程。

一、二项分布1.1义在概率论中，“二项分布”又称为“伯努利分布”，是指在若干次独立重复实验中，只有两种结果：实验成功和实验失败之间的概率分布。

1.2学期望与方差公式假设在每次实验中，实验成功的概率为$p$，共进行$n$次实验，则二项分布的概率函数为：$$P(X=x)=C_{n}^{x}p^{x}(1-p)^{n-x}$$其中，$x$为实验成功的次数，$C_{n}^{x}$为$n$个不同元素中取$x$个的组合数，即$$C_{n}^{x}=frac{n!}{x!(n-x)!}$$数学期望和方差用如下公式表示：$$E(X)=np$$$$D(X)=np(1-p)$$二、超几何分布2.1义超几何分布也称为超几何试验、超几何抽样或者超几何实验，可用于描述一种只有限数量的可能事件的抽样模型，其中，采用的方法是在一大堆里随机的抽取一定数量的元素。

超几何分布用参数$n$、$N$和$p$来描述，它的概率分布为：$$P(X=x)=C_{N}^{x}C_{n}^{x}p^{x}(1-p)^{N-x}$$ 其中，$x$为抽取到实验成功的次数，$N$为堆里元素的总数量，$p$为实验成功的概率，$n$为抽取的总次数。

2.2学期望与方差公式数学期望和方差用如下公式表示：$$E(X)=np$$$$D(X)=frac{n(N-n)p(1-p)}{N-1}$$三、推导3.1导期望根据定义可得：$$E(X)=sum_{x=0}^{n}xP(X=x) $$二项分布的推导：$$E(X)=sum_{x=0}^{n}xC_{n}^{x}p^{x}(1-p)^{n-x}$$$$E(X)=npsum_{x=0}^{n}C_{n}^{x}p^{x-1}(1-p)^{n-x}$$ 由于$C_{n}^{x}$是以$x$为底的等比数列，有：$$sum_{x=0}^{n}C_{n}^{x}p^{x-1}(1-p)^{n-x}=frac{1-(1-p)^{n} }{p}=frac{1-q^{n}}{p}=1$$所以：$$E(X)=np $$超几何分布的推导：$$E(X)=sum_{x=0}^{n}xC_{N}^{x}C_{n}^{x}p^{x}(1-p)^{N-x}$$$$E(X)=npsum_{x=0}^{n}C_{N}^{x}C_{n}^{x}p^{x-1}(1-p)^{N-x}$ $由于$C_{n}^{x}$是以$x$为底的等比数列，有：$$sum_{x=0}^{n}C_{N}^{x}C_{n}^{x}p^{x-1}(1-p)^{N-x}=frac{1-(1-p)^{N}}{p}=frac{1-q^N}{p}=frac{Np-(N-n)p}{p}=N-n+1$$ 所以：$$E(X)=np(N-n+1) $$3.2导方差根据定义可得：$$D(X)=E(X^{2})-E(X)^2$$二项分布的推导：$$D(X)=E(X^{2})-E(X)^2$$$$D(X)=sum_{x=0}^{n}x^2C_{n}^{x}p^{x}(1-p)^{n-x}-np^2$$ 由于$C_{n}^{x}$是以$x$为底的等比数列，有：$$sum_{x=0}^{n}x^2C_{n}^{x}p^{x}(1-p)^{n-x}=npsum_{x=0}^{n} xC_{n}^{x}p^{x-1}(1-p)^{n-x}=np^2frac{1-(1-p)^{n}}{p}=np^2f rac{1-q^{n}}{p}=np^2$$所以：$$D(X)=np(1-p) $$超几何分布的推导：$$D(X)=E(X^{2})-E(X)^2$$$$D(X)=sum_{x=0}^{n}x^2C_{N}^{x}C_{n}^{x}p^{x}(1-p)^{N-x}-n p^2(N-n+1)^2$$由于$C_{n}^{x}$是以$x$为底的等比数列，有：$$sum_{x=0}^{n}x^2C_{N}^{x}C_{n}^{x}p^{x}(1-p)^{N-x}=np(N-n +1)sum_{x=0}^{n}xC_{N}^{x}C_{n}^{x}p^{x-1}(1-p)^{N-x}$$$$=np(N-n+1)^2frac{1-(1-p)^{N}}{p}=np(N-n+1)^2frac{1-q^N}{p }=np(N-n+1)^2frac{Np-(N-n)p}{p}$$$$=np(N-n+1)^2frac{N-n}{p}=np[N(N-n+1)-n(N-n+1)]$$ 所以：$$D(X)=frac{n(N-n)p(1-p)}{N-1} $$四、总结从上文可以看出，二项分布和超几何分布的数学期望与方差公式都有具体的推导过程，数学期望与方差之间也有一定的关系。

二项分布方差证明过程嘿，朋友们！今天咱来唠唠二项分布方差的证明过程。

咱先说说啥是二项分布呀，就好比你扔硬币，不是正面就是反面，这就是很典型的二项分布嘛。

那二项分布的方差咋来的呢？这可有意思啦！你看啊，咱假设一个事儿，比如说你参加一个比赛，就两种结果，赢或者输。

每次赢的概率是固定的，这多像二项分布啊！那方差呢，就是衡量这个结果波动程度的。

要是方差大，那就说明结果很不稳定，一会儿赢一会儿输的；要是方差小呢，就说明结果比较稳定啦。

那怎么证明这个方差呢？咱就一步一步来。

就像你走路一样，一步一个脚印。

先把二项分布的公式摆出来，然后各种计算、推导。

哎呀，这过程就像解谜一样，可有意思啦！你想想，要是没有这个证明过程，咱怎么知道二项分布的方差到底是怎么回事儿呀。

就好像你不知道路该咋走，那不得迷路呀！你再想想，这证明过程就像盖房子，一砖一瓦都得垒好，少一块都不行。

每一步的计算，每一个式子的推导，都是在为这个“房子”添砖加瓦呢！等最后盖好了，哇，多有成就感呀！而且啊，这个证明过程也不是那么难理解的嘛。

只要你用心去想，去琢磨，就像你琢磨一道难题一样，总能弄明白的。

比如说，你可以把那些公式啊、符号啊，想象成你喜欢的东西，这样是不是就好理解多啦？或者把整个证明过程想象成一个游戏，你就是那个闯关的人，每过一关都特别有成就感。

总之呢，二项分布方差的证明过程虽然有点复杂，但绝对值得咱去好好研究研究。

等你弄明白了，你就会发现，哇，原来数学这么好玩呀！这可不是我瞎说，你自己去试试看就知道啦！所以啊，别害怕这个证明过程，大胆地去探索吧！就像探险家一样，去发现那些隐藏的宝藏。

相信我，你一定会有很多收获的！。

二项分布的期望和方差的详细证明在概率论与数理统计中，二项分布是一种非常重要的离散概率分布。

它在众多领域都有广泛的应用，例如质量控制、医学研究、市场调查等。

理解二项分布的期望和方差对于深入掌握概率统计的知识具有关键意义。

接下来，我们将详细证明二项分布的期望和方差。

首先，让我们回顾一下二项分布的定义。

如果进行 n 次独立的伯努利试验，每次试验成功的概率为 p，失败的概率为 1 p，那么成功的次数 X 服从参数为 n 和 p 的二项分布，记为 X ～ B(n, p)。

我们先来证明二项分布的期望。

期望（Expected Value），也称为均值，是描述随机变量平均取值的量。

设随机变量 X 服从二项分布 B(n, p)，则 X 可以表示为 X ＝ X₁＋X₂＋＋ Xₙ ，其中 Xᵢ（i ＝ 1, 2,， n）是相互独立且同分布的伯努利随机变量，即 Xᵢ取值为 1 表示成功，取值为 0 表示失败，且 P(Xᵢ＝ 1) ＝ p ，P(Xᵢ＝ 0) ＝ 1 p 。

那么 E(Xᵢ) ＝ 1×P(Xᵢ＝ 1) ＋ 0×P(Xᵢ＝ 0) ＝ p 。

因为期望具有线性性质，即对于任意随机变量 Y 和 Z 以及常数 a 和b ，有 E(aY ＋ bZ) ＝ aE(Y) ＋ bE(Z) 。

所以 E(X) ＝ E(X₁＋ X₂＋＋ Xₙ) ＝ E(X₁) ＋ E(X₂) ＋＋E(Xₙ) ＝ np 。

接下来证明二项分布的方差。

方差（Variance）是衡量随机变量取值相对于其期望的分散程度的量。

我们知道方差的定义为 Var(X) ＝ E(（X E(X)）²) ，也可以表示为Var(X) ＝ E(X²) （E(X)）²。

先计算 E(X²) ：E(X²) ＝∑x²×P(X ＝ x) （x 从 0 到 n）因为 X 服从二项分布 B(n, p) ，所以 P(X ＝ x) ＝ C(n, x) × p^x ×（1 p)＾（n x) 。

二项分布方差公式推导过程二项分布是统计学中非常重要的概率分布，它可以用来描述独立试验中发生成功次数的分布。

该分布具有两个参数，即成功概率p和试验次数n。

二项分布的方差表达式如下：VAR(X)=np(1-p)现在，让我们来看看二项分布方差公式的推导过程。

首先，我们需要讨论该分布的期望值。

期望值的计算公式如下： E(X) = np从这一式子可以看出，二项分布的期望值等于试验次数乘以成功概率。

其次，我们考虑二项分布的方差。

由于方差的定义：VAR(X)=E[(X-E(X))^2]所以，可以得出：VAR(X)=E[X^2] - [E(X)]^2接下来，我们推导出X的平方期望值。

由于独立试验的假设，我们可以得出：E[X^2] = (E[X])^2 + VAR(X)将期望值E(X)带入上式，即可得到：E[X^2] = np + np(1-p)将平方期望值带入方差定义中，得出：VAR(X)=np + np(1-p) - [np]^2计算结果为：VAR(X)=np(1-p)最后，我们需要检验推导的结果是否正确。

我们将以下参数带入推导的结果中：p=0.5， n=10VAR(X)=10 * 0.5 * (1-0.5)检验结果为：2.5因此我们可以确认推导的结果是正确的，二项分布的方差公式为：VAR(X)=np(1-p)。

通过这一推导，我们可以明确了二项分布的平方期望值、期望值以及方差之间的关系，有助于我们进行更全面深入的研究。

另外，了解二项分布的方差也可以帮助我们更好地分析数据，估算变量之间的相似性和变化情况，从而辅助决策过程。

总之，二项分布的方差公式是非常重要的，它可以用来定量描述随机变量变化情况，从而帮助我们更有效地进行数据分析和决策。

二项分布的期望与方差的证明二项分布是概率统计里面常见的分布，是指相互独立事件n次试验发生x次的概率分布，比较常见的例子。

种子萌发试验，有n颗种子，每颗种子萌发的概率是p，发芽了x颗的概率就服从二项分布。

如果还是迷茫，就听我说说故事，在古代，大概明末清初的时候，瑞士有个家族，叫伯努利家族，出了很多数学家，有一位叫詹姆斯·伯努利(James Bernoulli)的，比较喜欢做试验，他的试验有特点，是一系列的试验，没发生就是失败，而且每次的成功概率都是p，若果失败了就是q=(1-p)，只有这两种情况，后来人们给了这除了成功就是失败的性质一个比较抽象的名称，叫相互对立事件。

在这些试验中，每次得出的结果与其他次试验都不发生关系，同样人们也给了这种不发生关系的性质一个比较抽象的名称，叫相互独立事件，同时把这种试验叫做伯努利试验。

在n次伯努利试验中，发生x次的概率满足二项分布。

如果令q=(1-p)，那么很容易得出发生x次的概率为C{x，n}*p^x*q^(n-x)，因为决定该分布的只有n、p，所以为了简单起见，人们把x服从n，p的二项分布记做x～B(n，p)。

现在的目标是计算二项分布的期望和方差，在网上寻找二项分布的期望和方差大都给一个结果，np、npq，很难找到它是怎么来的。

好不容易查到，还是花钱才能看的，就那几步过程，有必要藏着盖着吗？今天我把过程写出来，让大家都了解了解，都是原创，互相学习，希望支持。

首先，不厌其烦地说一下期望与方差的关系，以便清晰思路。

期望用E表示，方差用D表示，一般把自变量记做ξ，如果对于结果为ξ的概率为Pξ那么，其期望为Eξ=∑ξ*Pξ，方差为Dξ=∑(ξ－Eξ)^2*Pξ，另外还有一个常见的量叫做标准差，一般用σ表示，σξ=√Dξ，根据方差的概念，可知：Dξ=∑(ξ－Eξ)^2*Pξ=∑(ξ^2＋Eξ^2－2*ξ*Eξ)*Pξ=∑(ξ^2*Pξ＋Eξ^2*Pξ－2*Pξ*ξ*Eξ)=∑ξ^2*Pξ＋Eξ^2*∑Pξ－2*Eξ*∑Pξ*ξ因为∑Pξ=1而且Eξ=∑ξ*Pξ所以Dξ=∑ξ^2*Pξ－Eξ^2而∑ξ^2*Pξ，表示E(ξ^2)所以Dξ=E(ξ^2)－Eξ^2下面计算数学期望,Eξ=∑{ξ =0，n}ξ*C{ξ，n}*p^ξ *q^(n-ξ)=∑{ξ =0，n}ξ*n!/ξ!/(n-ξ)!*p^ξ *q^(n-ξ)=∑{ξ =1，n}n!/(ξ-1)!/(n-ξ)!*p^ξ *q^(n-ξ)=n*p*∑{ξ =1，n}C{ξ-1，n-1}*p^(ξ-1)*q^(n-ξ)=n*p*(p+q)^(n-1)=n*p如果要计算方差，根据公式Dξ=E(ξ^2)－Eξ^2可得出结果，过程如下，Dξ=E(ξ^2)－Eξ^2=∑{ξ =0，n}ξ^2*C{ξ，n}*p^ξ *q^(n-ξ) －n*p*∑{ξ =0，n}ξ*C{ξ，n}*p^ξ *q^(n-ξ)=n*p*∑{ξ =1，n}ξ*(n-1)!/(ξ-1)!/(n-ξ)!*p^(ξ-1) *q^(n-ξ) －n*p*∑{ξ =1，n}ξ*C{ξ，n}*p^ξ *q^(n-ξ)=n*p*∑{ξ =1，n}p^(ξ-1)*q^(n-ξ)*ξ*(C{ξ-1，n-1}－C{ξ，n}＋C{ξ，n}*q) =n*p*∑{ξ =1，n}p^(ξ-1)*q^(n-ξ)*ξ*[C{ξ，n}*q－(C{ξ，n}－C{ξ-1，n-1})] =n*p*[∑{ξ =1，n}p^(ξ-1)*q^(n-ξ)*ξ*C{ξ，n}*q－∑{ξ =1，n-1}p^(ξ-1)*q^(n-ξ)*ξ*C{ξ，n-1}]=n*p*[∑{ξ =1，n}p^(ξ-1)*q^(n-ξ)*n!/(ξ-1)!/(n-ξ)!*q－∑{ξ =1，n-1}p^(ξ-1)*q^(n-ξ)*(n-1)!/(ξ-1)!/(n-1-ξ)!]=n*p*[∑{ξ =1，n}n*q*C{ξ-1，n-1}*p^(ξ-1)*q^(n-ξ)－∑{ξ =1，n-1}(n-1)*q*C{ξ-1，n-2}*p^(ξ-1)*q^(n-ξ-1)]=n*p*[n*q*(p+q)^(n-1)－(n-1)*q*(p+q)^(n-2)]=n*p*[n*q－(n-1)*q]=n*p*q以上就是二项分布的期望与方差的证明，过程比较简单，就是一个思路，要想更深入的领悟，就须要自己亲自地证明一遍了，也许你的方法将会更简单……。

二项分布期望和方差的推导过程二项分布是概率论和统计学中常用的一种离散概率分布。

它描述的是在一系列独立的伯努利试验中，成功事件发生的次数。

二项分布由两个参数n和p确定，其中n表示试验次数，p表示每次试验成功的概率。

二项分布的期望和方差是对其特征进行度量的重要指标。

下面将详细推导二项分布的期望和方差。

一、期望的推导：设X为二项分布的随机变量，表示成功事件发生的次数。

由于二项分布表示了一系列独立的伯努利试验，每次试验中成功和失败是互斥的，因此可采用计数的方法计算期望。

首先，我们先来看一次独立伯努利试验。

成功的概率为p，失败的概率为1-p。

成功事件发生的次数可以表示为：X=1，成功发生X=0，成功未发生根据期望的定义，我们有：E[X]=1*P(X=1)+0*P(X=0)根据概率的定义，P(X=1)=p，因为只有一次试验且成功的概率为p。

同理，P(X=0)=1-p。

带入上述式子，得到：E[X]=p*1+(1-p)*0=p这说明一次独立伯努利试验的期望等于成功的概率p。

接下来考虑n次独立伯努利试验的情况。

在n次试验中，成功事件发生的次数可以表示为：X=k，成功发生k次X=0，成功未发生根据期望的定义，我们有：E[X]=k*P(X=k)+0*P(X=0)要计算P(X=k)，我们需要考虑在n次试验中，成功发生k次的概率。

根据二项分布的定义，这个概率可以表示为：P(X=k)=C(n,k)*p^k*(1-p)^(n-k)其中C(n,k)表示从n个试验中选择k个成功事件的组合数。

带入上述式子，得到：E[X]=k*C(n,k)*p^k*(1-p)^(n-k)上式中k是变量，表示成功发生的次数。

为了计算期望E[X]，我们需要对k进行求和，考虑所有可能的取值。

因此，二项分布的期望可以表示为：E[X]=Σ[k=0,n]k*C(n,k)*p^k*(1-p)^(n-k)(从k=0到n的求和符号)这个求和式可以利用二项式定理展开并简化，最终得到：E[X] = np这就是二项分布的期望公式。

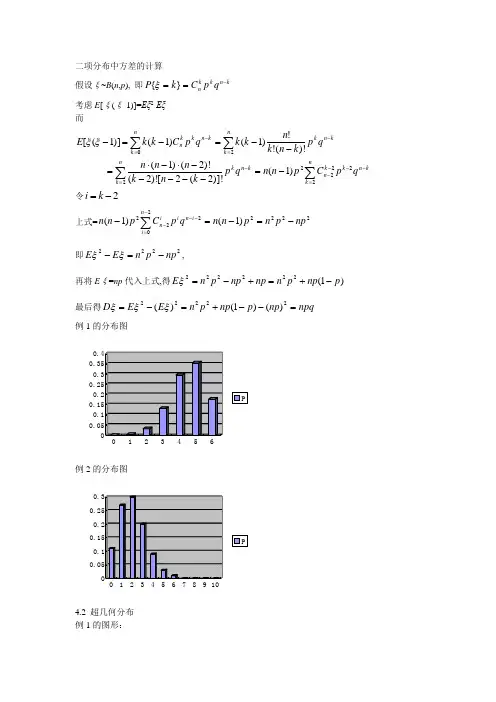
二项分布中方差的计算假设ξ~B (n ,p ), 即kn k k n q p C k P -==}{ξ考虑E [ξ(ξ-1)]=Eξ2-Eξ 而∑∑∑∑=----=-=-=--=-----⋅-⋅=--=-=-nk kn k k n nk k n k nk kn k nk kn kk nq p C p n n q p k n k n n n q p k n k n k k qp C k k E 22222220)1()]!2(2[)!2()!2()1()!(!!)1()1()]1([ξξ令2-=k i 上式=222220222)1()1(np p n p n n q p Cpn n n i i n i in -=-=-∑-=---即2222np p n E E -=-ξξ,再将E ξ=np 代入上式,得)1(222222p np p n np np p n E -+=+-=ξ 最后得npq np p np p n E E D =--+=-=22222)()1()(ξξξ 例1的分布图例2的分布图4.2 超几何分布 例1的图形：例2的图形：定义4.2 设N 个元素分为两类, 有N 1个属于第一类, N 2个属于第二类(N 1+N 2=N ). 从中不重复抽样取n 个, 令ξ表示这n 个中第一类元素的个数, 则ξ的分布称为超几何分布,),....,1,0()(21n m CC C m P nNm n N m N ===-ξ规定: 如n <r , 那末0=rn C由概率分布的性质可知1)(0==∑=n m m P ξ, 即1021=∑=-nm nNm n N m N C C C可得组合的性质n N N nk k n N k N C C C21210+=-=∑ 计算ξ的数学期望和方差有两种方法第一种, 按定义∑∑∑∑===-=-++-+--⋅+----=+--⋅-⋅=====nm n Nnm n N nm n Nm n Nm N n m m n N m n N m N m N C N m n N m n N m N m N m C CC C mm mP E 1221111221100)!11()!11(!)!11()!1()!1()!()!(!)!(!!1)(21ξξ令k =m -1, 则上式=np N N n n N n N n N n N N C C N C C C N n N n Nn k kn N k N nN=⋅=---⋅-==---=---∑111111111)!()!1()!1()!(!!21其中NN p 1=为只抽一次抽到元素N 1的概率 因此放回抽样(二项分布)与不放回抽样(超几何分布)的数学期望是一样的.∑∑∑∑∑=-----=-=-=-=-=⋅+-----=⋅--=-==-=-n m m n N m N nN nm mn N n N nm mn N n N nm nNm n N m N n m C C C N N C m N m N C N N C m N m N C C C C m m m P m m E 2)2()2(2211211112112212221)1()!22()!2()!2()1()!()!2(!1)1()()1()]1([ξξξ令k =m -2,上式=221120)2(211)1()1(21---=---⋅-=-∑n N nN n k kn N k N n N C C N N C C C N N)1()1()1()!()!2()!2()!(!!)1(1111---=---⋅--=N N n n N N n N n N n N n N N N因此NnN N N n n N N E E E 1112)1()1()1()]1([+---=+-=ξξξξ11)1())(()1()]()([)1(][)1(][)1()]1()1()1)(1[()1()1()1()1()1()1()1()1()(21211211121211211211121112212111221211122--=--⋅⋅⋅=---=----==-++--==-+--++--=----+--==----+--==-+---=-=N n N npqN n N N N N N n N N n N N N nN N N N N n N N N nN N N nN N nN N N nN N N nN N nN N N N nN N N nN N nN N N N nN N N N n N nN N N N N n N N nN N n n N N N N n N nN N N n n N N E E D ξξξ 其中q =1-p另有一种办法计算ξ的数学期望，假设ξi 是第i 次抽到第一类元素的个数，因为只是1次，当然不是1就是0，因此服从0-1分布，且有),...,2,1(,)0(,)1(21n i q NNP p N N P i i =======ξξ,则),...,2,1(1n i p NN E i ===ξ因此np NN n nE E E E E E i nn =⋅==+++=+++=12121)(ξξξξξξξξ整个方法同二项分布时的相应方法一样，只是各ξi 间并非相互独立，但和的期望等于期望的和这条性质并不要求和中各项的随机变量相互独立。

二项分布公式推导过程
二项分布是描述重复进行n次独立实验中成功次数的概率分布。

假设每次实验成功的概率为p，失败的概率为1-p，成功的概
率不变且相互独立。

现在来推导二项分布的公式。

首先，考虑进行了n次实验中成功k次的概率。

在这n次实验中，有k次成功和n-k次失败。

成功的概率是p，失败的概率
是1-p，因此成功k次失败n-k次的概率可以表示为p^k*(1-
p)^(n-k)。

接下来，考虑这n次实验中，成功的次数可以发生在不同的位置上。

例如，在第1次和第2次实验中均成功，可以表示为SSFFFF...F，其中S表示成功，F表示失败。

一共有n-k个F，而这n次实验中有k次成功，所以成功的位置可以有C(n,k)种
组合，即组合数。

因此，进行了n次实验中成功k次的概率就是这n次实验中，
成功的位置组合数C(n,k)乘以每种组合中出现的概率p^k*(1-p)^(n-k)。

即二项分布的公式为：
P(X=k) = C(n,k) * p^k * (1-p)^(n-k)
其中，P(X=k)表示进行n次实验中成功k次的概率，C(n, k)表
示组合数，p表示成功的概率，n表示总的实验次数。