九下第八章统计和概率的简单应用

8.5 概率帮我们估计教材分析：本节课主要讲述的是概率帮你做估计。

不确定现象是大量存在于自然界和人类社会中概率正是对这种现象的一种数学描述，它能帮助我们更好地认识不确定现象，并对生活中的一些不确定情况作出决策。

在七年级上、下册中，教材已经呈现了随机事件并介绍了随机事件的等可能性、随机事件的概率等有关基本概念。

通过八年级的学习学生，经历了对数据的收集、整理、分析的过程，了解总体、个体、样本掌握了频数、频率、频数分布直方图等相关知识。

本节课为了帮助学生更好地认识随机现象，通过一个涉及两步实验的事件作为课堂试验活动，让学生逐步计算一个随机事件发生的频率；由大量重复试验的结果观察其中的规律性并利用类比的方法归纳出大量重复试验的频率趋近于理论概率这一规律性；为以后利用试验或模拟试验的方法估计一些复杂的随机事件发生的概率起到承前启后的作用。

教学目标：1．通过操作“摸球游戏”的过程，会用概率估算某一群体的数目．2．经历建立“概率模型”的过程，会用频率估算概率．教学重点：会用频率估算概率。

教学难点：会用概率估算某一群体的数目。

情感、态度与价值观：1.培养学生实事求是的科学态度，发展学生合作交流的意识和能力。

2.体会到根据实际情境设计出合理的模拟试验来研究问题的思想方法，积极参与数学活动。

通过实验提高学习数学的兴趣。

3.提高自身的数学交流水平，增强与人合作的精神和解决实际问题的能力，发展辩证思维能力。

一、知识回顾：1、学习委员调查本班学生课外阅读情况，对学生喜爱的书籍进行分类统计，其中“古诗词类”的频数为12人，频率为0.25，那么被调查的学生人数为．2、在一个不透明的袋子中装有4个红球和3个黑球，它们除颜色外其它均相同，从中任意摸出一个球，则摸出黑球的概率是（）A．17B．37C．47D．57设计意图：通过一组练习，掌握频率与频数的关系。

二、思考与探索：袋中装有白球和红球共20个，每个球除颜色外都相同，袋中有多少个白球？用什么方法解决这个问题？在做这个游戏中需要注意哪些问题？（每组一人摸球，一人记载，其他同学监督，一组20次）预测一下，袋中白球的个数？（我们将各组摸球红球的次数组合，我们看一看统计的情况）设计意图：让学生亲身经历试验的过程，小组合作收集数据以及得出结论的过程中感受到了数学试验的乐趣，进一步增强了学生合作交流的意识与能力。

初三数学概率与统计应用概率与统计是数学中的重要分支，也是我们日常生活中经常接触到的概念。

概率与统计的应用广泛，涉及到许多领域，如商业、医学、经济等。

在初三阶段，掌握概率与统计的基本知识，并学会将其应用于实际问题解决，是我们学习数学的重要任务之一。

本文将探讨初三数学概率与统计的应用。

一、概率的应用概率是描述事物发生可能性大小的数值，通过概率，我们可以判断事物发生的可能性，进而做出合理决策。

以下是几个概率应用的实例。

1. 抽奖活动在许多抽奖活动中，我们需要根据已知的概率来计算获奖的可能性。

假设某次抽奖活动共有100个人参与，每个人的中奖概率为1%，那么我们可以通过概率计算得知，大约有1人会获得奖品。

这样的数据分析可以帮助组织者合理安排奖品数量，提高活动的公平性。

2. 游戏策略在玩一些策略类游戏时，概率的应用也非常重要。

比如，在玩扑克牌游戏时，我们可以通过计算概率来决定是否进行押注。

如果手中的牌组合形成了一副较强的牌型，那么我们就可以根据概率进行更大的押注，以获得更高的胜算。

二、统计的应用统计是描述和分析数据的一种方法，通过统计，我们可以观察数据的规律、趋势，从而得出结论。

以下是几个统计应用的实例。

1. 调查问卷在进行社会科学研究或者市场调查时，我们常常会使用调查问卷来收集数据。

通过统计问卷中的各项数据，我们可以对特定问题或者群体的情况进行分析，并根据统计结果做出相应决策。

例如，在进行市场调研时，我们可以通过统计数据得知消费者对某个产品的需求程度，从而决定是否在该领域进行投资。

2. 商品销售分析商家在销售商品时，往往会根据过去的销售数据进行统计分析，以预测未来的销售趋势，并作出相应的决策。

比如，某商店在过去一年的销售数据中发现，夏季时销量明显上升，那么在接下来的夏季，商家可以增加该类商品的进货数量，以满足潜在的销售需求。

总结：概率与统计的应用为我们提供了一种科学的思维方式，帮助我们更好地理解和解决实际问题。

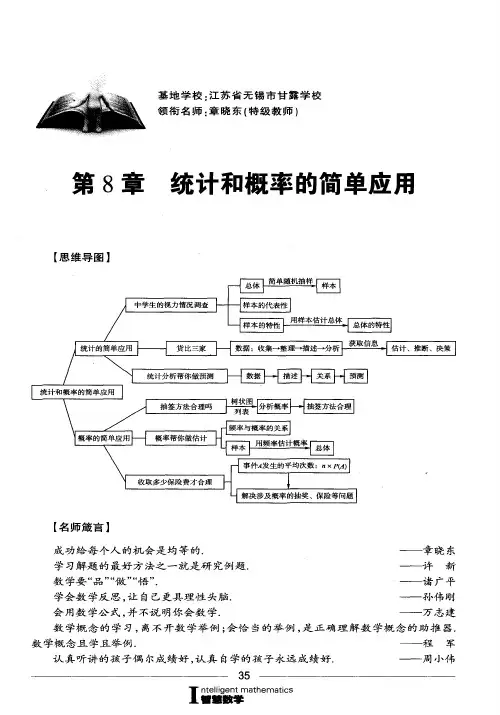
第8章统计和概率的简单应用8.1 中学生的视力情况调查知识点一般地，从个体总数为N的总体中抽取容量为n的样本（n＜N），且每次抽取样本时，总体中的每个个体被抽到的可能性相同，这种抽样的方法叫做简单随机抽样．要识别统计的一些误用，如数据表选取不合理，统计图表表示不合理等；用样本估计总体时，样本必须有足够的代表性，需要强调一点：样本只能近似地反映总体的情况；利用统计知识进行相关运算时，弄清相关概念，合理进行运算．8.2 货比三家数据的获取可以是多渠道的，我们可以从中获得许多有用的信息，然而获得的信息有时不一定是准确可信的，因此我们必须对所获得的数据进行加工处理，以形成对客观现象（事情）理性的、正确的认识，正所谓的“货比三家不吃亏”．8.3统计分析帮你做预测8.4 抽签方法合理吗1．一定会发生的事件叫________事件；一定不会发生的事件叫_________事件；它们通称_________事件；无法确定是否会发生的事件叫_______事件．2．无论是试验的所有可能产生结果是有限个，还是无限个，具备哪几个特征的试验结果才具有等可能性？①在试验中发生的事件都是______事件；②在每一次试验中有且只有_个结果出现；③每个结果出现机会___________．8.5 概率帮你做估计温故频数：每个对象出现的次数称为频数．频率：而每个对象出现的次数与总次数的比值称为频率．思考：频率与概率之间的关系？小结：大量重复试验所得到的随机事件发生的实际频率接近于该事件发生的理论概率．8.6 收取多少保险费才合理一般地，如果随机事件A发生的概率是P（A），那么在相同的条件下重复n次试验，事件A发生的次数的平均值m为n×P（A）．练习1、为了估计湖中有多少条鱼，先从湖中捕捉50条鱼做记号，然后放回湖里，经过一段时间，等带记号的鱼完全混于鱼群中之后，再捕捞第二次，鱼共200条，有10条做了记号，则估计湖里有多少条鱼（）A．400条 B．500条 C．800条 D．1000条2、一个不透明的布袋里装有4个球，其中3个红球，1个白球，它们除颜色外其余都相同．（1）求摸出1个球是白球的概率；（2）摸出1个球，记下颜色后放回，并搅匀，再摸出1个球．求两次摸出的球恰好颜色相同的概率（要求画树状图或列表）；（3）现再将n 个白球放入布袋，搅匀后，使摸出1个球是白球的概率为，求n 的值．3、某校为了解2014年八年级学生课外书籍借阅情况，从中随机抽取了40名学生课外书籍借阅情况，将统计结果列出如下的表格，并绘制成如图所示的扇形统计图，其中科普类册数占这40名学生借阅总册数的40%． 类别科普类 教辅类 文艺类 其他 册数（本）128 80 m48（1）求表格中字母m 的值及扇形统计图中“教辅类”所对应的圆心角a 的度数；（2）该校2014年八年级有500名学生，请你估计该年级学生共借阅教辅类书籍约多少本？4、学习成为现代人的时尚，某市有关部门统计了最近6个月到图书馆的读者的职业分布情况，并做了下列两个不完整的统计图．（1）在统计的这段时间内，共有 万人次到图书馆阅读，其中商人占百分比为 %；（2）将条形统计图补充完整；类别 科普类 教辅类 文艺类 其他册数（本） 12880 m 48 47（3）若5月份到图书馆的读者共28000人次，估计其中约有多少人次读者是职工？5、某校为了了解学生孝敬父母的情况（选项：A．为父母洗一次脚；B．帮父母做一次家务；C．给父母买一件礼物；D．其它），在全校范围内随机抽取了若干名学生进行调查，得到如图表（部分信息未给出）：根据以上信息解答下列问题：学生孝敬父母情况统计表：选项频数频率A m0.15B60 pC n0.4D48 0.2（1）这次被调查的学生有多少人？（2）求表中m，n，p的值，并补全条形统计图．（3）该校有1600名学生，估计该校全体学生中选择B选项的有多少人？。