信号与系统(第三章周期信号的傅里叶级数展开)

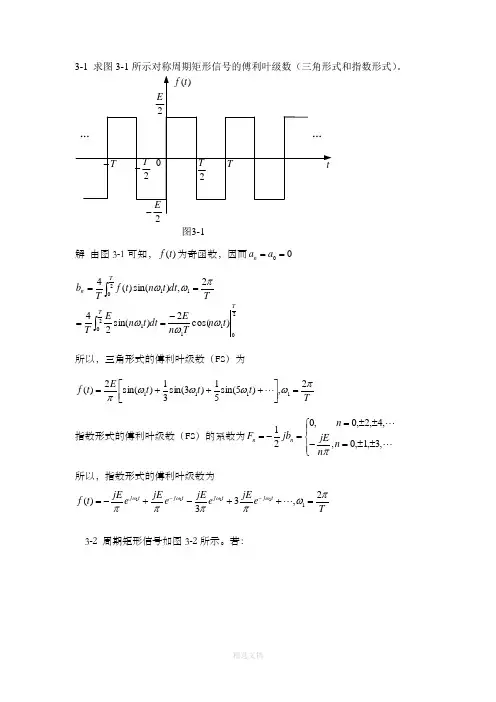
3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。

图3-1解 由图3-1可知，)(t f 为奇函数，因而00==a a n2112011201)cos(2)sin(242,)sin()(4T T T n t n T n Edt t n E T T dt t n t f T b ωωωπωω-====⎰⎰所以，三角形式的傅利叶级数（FS ）为T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=⎥⎦⎤⎢⎣⎡+++=指数形式的傅利叶级数（FS ）的系数为⎪⎩⎪⎨⎧±±=-±±==-= ,3,1,0,,4,2,0,021n n jE n jb F n n π所以，指数形式的傅利叶级数为Te jE e jE e jEe jEt f t j t j t j t j πωππππωωωω2,33)(11111=++-+-=--3-2 周期矩形信号如图3-2所示。

若：图3-22τT-2τ-重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10=求直流分量大小以及基波、二次和三次谐波的有效值。

解 对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛====⎰⎰--22sin 12,)(1112212211τωττωππωττωωn Sa T E n n E dt Ee T T dt e t f T F tjn TT t jn n则的指数形式的傅利叶级数（FS ）为∑∑∞-∞=∞-∞=⎪⎭⎫⎝⎛==n tjn n tjn ne n Sa TE eF t f 112)(1ωωτωτ其直流分量为T E n Sa T E F n ττωτ=⎪⎭⎫ ⎝⎛=→2lim100 基波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-2sin 2111τωπEF F 二次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-22sin 122τωπEF F 三次谐波分量的幅度为⎪⎭⎫ ⎝⎛⋅=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得s T s rad 441102,/10-⨯==πω 将各参数的值代入，可得直流分量大小为V 110210201046=⨯⨯⨯--基波的有效值为())(39.118sin 210101010sin 210264V ≈=⨯⨯⨯- πππ二次谐波分量的有效值为())(32.136sin 251010102sin 21064V ≈=⨯⨯⨯- πππ三次谐波分量的有效值为())(21.1524sin 32101010103sin 2310264V ≈=⨯⨯⨯⨯- πππ3-3 若周期矩形信号)(1t f 和)(2t f 的波形如图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1= ，V E 1=； )(2t f 的参数为s μτ5.1=，s T μ3= ，V E 3=，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3）)(1t f 与)(2t f 的基波幅度之比； （4）)(1t f 基波与)(2t f 三次谐波幅度之比。

周期信号的傅里叶级数展开：1． 三角形式： 周期信号()f t ，周期T ，基波频率12w Tπ=，所构成的完备正交函数集：三角函数集{}11cos ,sin nwt nwt ； ()0111()cos sin n n n f t a a nw t b nw t ∞==++∑其中：2021()TT a f t dt T -=⎰2122()cos TT n a f t nw tdt T -=⎰2122()sin TT n b f t nw tdt T -=⎰ 注意: (1) 展开条件：狄利赫利条件 （2） 另外一种形式：011()cos()nn n f t c cnw t ϕ∞==++∑其中：00c a =n c =nn nb tg a φ=-（3）物理意义： （4）幅度谱和相位谱2. 指数形式： 完备正交函数集 ：复指数函数集{}1jnw t e1()jnw tnn f t F e∞=-∞=∑其中1221()Tjnw t T n F f t e dt T --=⎰注意：（1）幅度谱和相位谱nj n n F F e φ= ：偶谱和奇谱与三角形式间的关系（2）两种级数间的关系 3. 函数()f t 满足对称性的级数展开： （1） 偶函数：011()cos n n f t a a nw t ∞==+∑0n b =或011()cos()n n n f t c c nw t ϕ∞==++∑，00c a =||n n c a =0,0,0n n n a a ϕπ>⎧=⎨<⎩（2）奇函数：11()sin n n f t b nw t ∞==∑00n a a ==或011()cos()n n n f t c c nw t ϕ∞==++∑，00c =||n n c b =,02,02nn nb b πϕπ⎧->⎪⎪=⎨⎪<⎪⎩（3）奇谐函数：()()2T f t f t =-±其傅里叶级数展开式中仅含奇次谐波分量，即： 0240a a a ====2460b b b ====4. 典型周期矩形脉冲的傅里叶级数信号()f t ，周期为T ，脉宽为τ，脉幅为E（1）三角形式011()cos nn f t a anw t ∞==+∑0n b =其中：2202211()T T E a f t dt Edt T T Tτττ--===⎰⎰211222cos 2n E a E nw tdt Sa nw T T ττττ-⎛⎫== ⎪⎝⎭⎰ 谐波形式：011()cos()n n n f t c c nw t φ∞==++∑其中：00c a =n nc a =， {0,0,0n n n a a ϕπ>=<（2）指数形式：1()jnw t n n f t F e ∞=-∞=∑其中：11222211()T jnw tjnw t T n F f t e dt Ee dt T T ττ---==⎰⎰112E Sa nw T ττ⎛⎫=⎪⎝⎭（3）幅度谱和相位谱的特点 谱线间隔和频谱宽度二．傅里叶变换 ()()jwt F w f t e dt ∞--∞=⎰1()()2jwt f t F w e dw π∞-∞=⎰特点：（1）()()()j w F w F w e ϕ=幅频函数和相频函数（2）变换条件：|()|f t dt ∞-∞<∞⎰ （3）()f t 也是由许多频率分量构成三．常见信号的傅里叶变换对 单边指数衰减信号,0()0,0t e t f t t α-⎧>=⎨<⎩，0α> ↔1()F w jw α=+ 双边指数衰减信号||,0(),0t t te tf t ee t ααα--⎧>==⎨<⎩ ↔222()F w w αα=+矩形脉冲(),2f t E tτ=<↔ ()()2F w E Sa w ττ=符号函数()sgn()f t t = ↔2()F w jw=冲击函数()()f t t δ= ↔ ()1F w = ()()f t t δ'=↔ ()F w jw =()()()n f t t δ=↔ ()()nF w jw = 直流信号()1f t = ↔ ()()2F w w πδ=()f t jt =-↔ ()()2F w w πδ'=()()nf t jt =-↔()()()2n F w w πδ=阶跃信号()()f t u t = ↔()1()F w w jwπδ=+四．傅里叶变换的性质 1.线性性2.奇偶虚实性：()f t 为实函数()()()cos ()sin jwtF w f t edt f t wtdt j f t wtdt ∞∞∞--∞-∞-∞==-⎰⎰⎰（1）()f t 为实偶函数，虚部()()sin 0X w f t wtdt ∞-∞==⎰ （2）()f t 为实奇函数，实部()()cos 0R w f t wtdt ∞-∞==⎰3. 对称性4.时移性5. 尺度变换：时域压缩，频谱扩张 时域扩张，频谱压缩 时域反褶，频谱反褶6.频移性：00()()jw tF f t e F w w ⎡⎤=-⎣⎦[][]001()cos ()()2F f t wt F w w F w w =-++[][]001()sin ()()2F f t wt F w w F w w j=--+ 7.时域微分：[]()()F f t jwF w '=()()()()n nF f t jw F w ⎡⎤=⎣⎦8.频域微分：[]()()F jtf t F w '-=()()()()n n F jt f t F w ⎡⎤-=⎣⎦9.时域卷积：()()()1212()F f t f t F w F w *=⎡⎤⎣⎦ 10.频域卷积：五．周期信号的傅里叶变换：（1） 周期信号的傅里叶级数展开式：1()jnw tnn f t F e ∞=-∞=∑（2） 周期信号的傅里叶变换：1()2()nn F w F w nw πδ∞=-∞=-∑特点：（ⅰ）频谱为冲击谱 （ⅱ）强度为2n F π（ⅲ）谱线位于谐波处（1nw ）（ⅳ）()1120211()|Tjnw t jwt T n w nw F f t e dt f t e dt T T∞--=-∞-==⎰⎰()101|w nw F w T==其中：0()f t 为周期信号的第一个脉冲， ()0F w 为0()f t 的傅里叶变换。

第3章 周期信号的傅里叶级数表示一、计算题1．求如图3-1所示信号的傅里叶级数。

答：（1）求三角傅里叶级数。

傅里叶级数展开表达式图3-10111()[cos()sin()]2n n n a f t a nw t b nw t ∞==++∑利用分部积分三角傅里叶级数为（2）指数形式傅里叶级数展开：11()()jnw t n f t F nw e ∞=-∞=∑，其中011011()t T jnw t n t F f t e dt T +-=⎰求指数傅里叶级数。

指数傅里叶级数为2．将如图3-2所示的三角形信号在时间区间(,)ππ-上展开为有限项的三角傅里叶级数，使其与实际信号间的方均误差小于原信号()f t 总能量的1％。

写出此有限项三角傅里叶级数的表达式。

图3-2解：如图3-2所示三角形信号的数学表达式为由()f t 在(,)ππ-上的偶对称特性知其傅里叶系数0n b =。

又展开的时间区间为(,)ππ-，故2T π=，从而1Ω=。

下面求系数0a 和n a 。

于是在(,)ππ-上，另一方面，信号的总能量若取()f t 傅里叶级数中第一项来近似()f t ，则方均误差为再考虑取()f t 傅里叶级数中前两项来近似()f t ，则方均误差为由于满足要求，所以此有限项三角傅里叶级数的表达式为24()cos 2A Af t t π≈+3．求如图3-3所示信号f （t ）的傅里叶级数。

图3-3答：f'（t ）、f''（t ）的波形如图3-4（a ）、（b ）所示，于是得f''（t ）的傅里叶系数为图3-4故f （t ）的傅里叶系数为所以f （t ）的傅里叶级数为111(1)()2222n jn t jn tn n n jf t A e e n π∞∞⋅ΩΩ=-∞=-∞-=+=+∑∑ （原书中有错，第二项的2j n 应改为2jπ） 讨论傅里叶级数的时域微分性质：这样，若已知f （k ）（t ）的傅里叶系数，则f （t ）的傅里叶系数这里注意此式不适用于n=0的情况。