184氢原子光谱玻尔氢原子理论
- 格式:ppt
- 大小:419.00 KB
- 文档页数:21

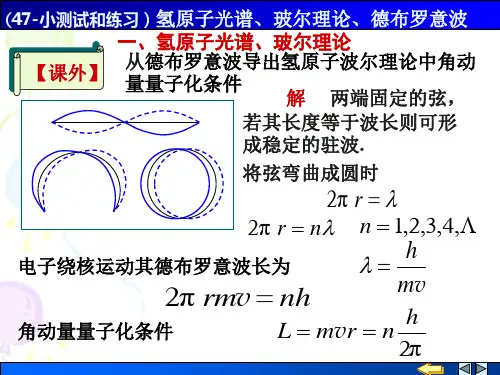

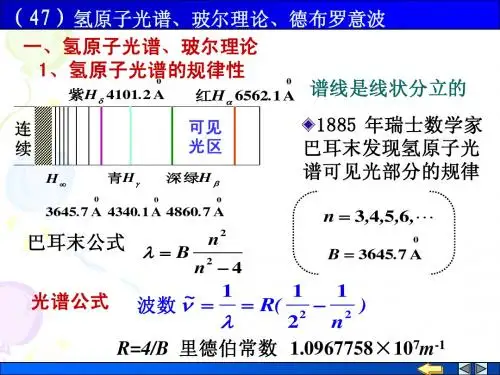




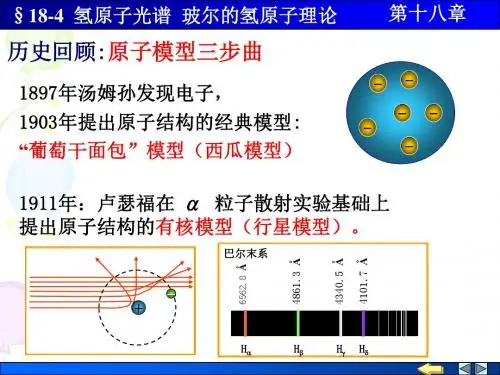
1第4节 氢原子光谱 玻尔理论一、 氢原子光谱422-=n n B λ,∞=,,5,4,3 nA =7.3645B αH βH γH ∞H∞→n ,B =∞λ巴耳末系,∞H :线系极限B =∞λ=A 7.3645:线系极限波长波数ν~:沿波线单位长度内波的个数 cνλν==1~λ)121()121(4)41(1411~2222222n R n B n B n n B -=-=-=-==λν ,5,4,3=n里德伯公式1710096776.14-⨯==m BR :里德伯恒量帕邢系:)131(1~22n R -==λν, ,6,5,4=n 原子光谱实验规律:“原子光谱都是彼此分立的线状光谱,每一条光谱线的波数由 两个光谱项的差值决定” 里兹并合原理)()(~n T k T -=ν,N k n ∈,,k n > )(k T 、)(n T :光谱项氢原子:2)(k R k T =,2)(nRn T =碱金属原子:2)()(α+=k R k T ,2)()(β+=n Rn T k 、n 都给定,给出一条光谱线的波数k 一定,所有n 的取值对应的谱线构成一个谱线系 k 不同,给出不同的谱线系 二、 玻尔理论1、 原子的有核模型1911,卢瑟夫,α粒子散射实验有核模型与经典理论矛盾 按照经典理论:原子光谱应是连续的,原子是不稳定的2、 玻尔的氢原子理论c2(1) 定态假设:原子只能处在一系列具有不连续能量的 稳定状态:定态,不辐射电磁波 定态1, 定态2, , 1E , 2E , , 轨道1, 轨道2, , (2) 跃迁假设:n E 的定态→k E 的定态 光子频率hE E nk -=νn E <k E ,吸收一个光子,n E >k E ,放出一个光子(3)角动量量子化假设:电子绕核转动的角动量: n hnL ==π2, ,3,2,1=n n :量子数π2h = :约化普朗克常数,SI :π2h= =Js 341005.1-⨯三、 氢原子结构和氢原子光谱 1、 轨道半径 20224r e r V m πε= (1) n m V r L == ,3,2,1=n (2),(V m r P r L⨯=⨯=,θθs i n s i n r m V rP L ==) 222023141 n r e mr πε=,22204n me r ⋅= πε, ,3,2,1=n 1=n ,A ==529.042201mer πε 2=n ,2122⋅=r r3=n ,2133⋅=r r21n r r n ⋅=<<<321r r rA=529.01r :玻尔半径 结论:电子的轨道半径是量子化的 2、 定态能量r e mV E 022421πε-=,20224re r V m πε=,r e mV 022821πε= 210202188n r e re E ⋅-=-=πεπε, ,3,2,1=nVm e31=n ,eV r e E 6.1381021-=-=πε,2=n ,eV E E 4.32/212-==3=n , ,51.13/213eV E E -==, 21/n E E n = <<<321E E E1=n 的定态:基态,1>n 的定态,激发态 结论:氢原子的定态能量是量子化的 每一个定态能量称为一个能级∞=n 4=n51.1-3=neV 4.3-2=neV 6.13-1=n3、 氢原子光谱氢原子 n E →k E ,k n >辐射光子频率h E E k n -=ν=)(12121k E n E h -=)11(221nk h E --波数==c νν~)11(221n k hc E --,k n > 令hc E R 1-=,==λν1~)11(22n k R -,k n > hcER 1-==1710097373.1-⨯m 例:赖曼系中波长最短的谱线光子能量是多少? 答:eV 6.13例:巴耳末系中波长最短的谱线光子能量是多少? 答:eV 4.3例:写出氢原子光谱各谱线系的极限波数表达式解:==λν1~)11(22n k R -,∞→n ,2)(~k R =∞ν 赖曼系 (1=k ), R =∞)(~赖ν=1710097.1-⨯m 巴耳末系(2=k ),1710274.04)(~-⨯==∞m R 巴ν 5=n 赖曼系4四、 玻尔理论的缺陷氢原子及 类氢离子光谱 H , +He ,+2Li ,+3Be Z= 1, 2, 3, 4碱金属元素的原子光谱,光谱的精细结构 塞曼效应,谱线宽度、强度、偏振逻辑上,玻尔理论自相矛盾 认识原子结构的里程碑 “定态”、“能级”、“跃迁” 例:氢原子由量子数为n 的定态→(1-n )的定态 求:(1)辐射光子频率1-→n n ν(2)n 很大时,1-→n n νn ν≈ n ν:电子在第n 轨道上的转动频率解:(1)1-→n n ν=22121211)1(12])1([1n n n h E n E n E h h E E n n --⋅-=--=-- =22102)1(128n n n h r e --⋅πε (10218r e E πε-=) (2)n ν=nn nn n r m V m V r V ππ222= (20224n n n r e r V m πε=) =31020214214n h r e n r e n ⋅=⋅πεππε ( n r mV n n =,21n r r n ⋅=)n 很大时,1-→n n ν=22102)1(128n n n h r e --⋅πε310214nh r e ⋅≈πε=n ν 对应原理:当量子数n 很大时,量子方程应过渡到经典方程 经典理论是量子理论在n 很大时的极限例:氢原子某谱线系的极限波长为A 3647,其中一条谱线波长为A6565 求:该谱线对应的氢原子初态和末态的能级能量 (1710097.1-⨯=m R )解:==λν1~)11(22n k R -,∞→n ,21k R =∞λ,2==∞λR k =λ1)121(22n R -,221211n R -=λ,R nλ14112-==R R λλ44- 344=-=R Rn λλ初态3=n ,eV E E 51.13/213-==末态2=n ,eV E E 4.32/212-==5光学发展简史牛 顿:微粒学说,惯性运动的微粒流直线传播、反射、折射牛顿环 惠更斯:波动学说,波动直线传播、反射、折射 干涉、衍射 几何光学1801年,杨氏,双缝干涉,光的波长1815年,菲涅耳,惠更斯-菲涅耳原理,直线传播、反射、折射、 干涉、衍射 1817年,杨氏,光是横波,偏振 1865年,麦克斯韦,光是电磁波19世纪末20世纪初,普朗克,爱因斯坦,光量子假说νh E =,λhP =光的波粒二象性。