- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
进一步的实验证实: 第二激发态电势为 6.7 v
电离电势为 10.4 v
11
注意几个概念:
1. 状态能量:原子系统处于某激发态时所具有的能量。
2. 激发能量:原子从基态被激发到某一激发态,外界所 提供的能量
某状态的激发能量 = 该状态的状态能量 - 基态能量
3. 氢原子的状态能量 氢原子中电子的状态能量
B
1
赖曼系:
~
1
R(112
1 n2
)
n 2,3,4,
紫外区
帕邢系:
~
1
R(
1 32
1 n2
)
n 4,5,6,
布喇开系:
~
1
R(
1 42
1 n2
)
n 5,6,7,
红外区
普芳德系:
~
1
R(512
1 n2
)
n 6,7,8,
3. 广义的巴尔末公式:(氢原子光谱的其它线系)
~
R(
1 k2
1 n2
)
k 1,2,3,
解: E 0 ,E1 13 6 结合能 E E1 0 (13 6) 13 6(eV )
例2:将氢原子中n=2 的电子搬到无限远处需要多少能量?
解: E2 E
激发能量
13 6 ? 0 4
? 13 6 (eV) 4
13
三、玻尔理论的成功及局限性
1. 成功 (对氢原子、类氢离子、一价的 Na, K , Li )
c c
(
1 k2
1 n2
)
令:
R
me 4
8
2 0
h3c
Rc(
1 k2
1 n2
)
En
me 4 802n2h2
这是什么?
~
1
c
R(
1 k2
1 n2
)
得: R 1 097373107 m1
——广义的巴尔末公式!
而 实验值: R 1 096776107 m1
每一个光谱项都对应一个确定能级:
R n2
En hc
En
136 n2
E1、E41、E91
一个能级将对应一条圆轨道
n1
2
3 4
5
3)电子运动的速度
由:
mV r
2
e2
4 or
2
Vn
4e20
1 n
n 1,2,
n、速度 Vn
在r1的轨道上:
V1 C
1 137
V1106m s1
7
4. 氢原子光谱的理论解释
1)里德伯常数的理论值
根据:
En
h
Ek
me4
802h3
8
2)解释分立的谱线
能级不连续 v 不连续,
不同的v对应不同的谱线。
3)解释谱线系
5 4
为什么存在谱线系? 3
为什么有些谱线在短波区、
有些长波区? 什么情况下
在什么区?
2
看:E E n 1
En Ek hh
0 85eV 1 51eV 3 39eV
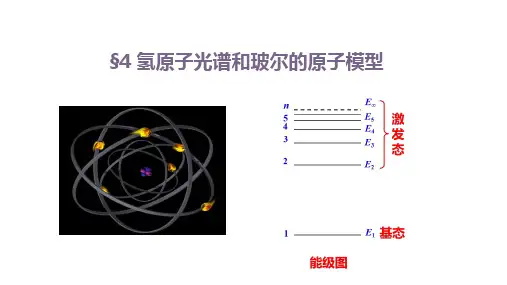
13 6eV 氢原子能级图
n k 1, k 2,
其中: 实验表明:
R k2
和
R n2
称为光谱项
原子具有线光谱;
各谱线间具有一定的关系;
每一谱线的波数都可表达 为两个光谱项之差。 2
经典理论的解释:
1)根据原子的有核模型,原子能量为:
E Eek U
1 2
meV
2
f向心
moVr2
e2
4or2
(
e2
4or
)
e2
8or
向心力作用 电子加速运动 辐射电磁波
0
5
10 15(V)
10
300
阴极 栅极 板极
汞
200
蒸
A
K 气G P
100
V
0
5
10 15(V)
V=4.9v
为什么?
只能有一个解释: 4.9 eV 恰好是汞原子某能级间的能量差
实验证实:
汞原子基态能 – 第一激发态能量=4.9 eV
汞原子发射的光谱: 253.7nm
代入光子能量公式: h hc 4.89eV E
大 学 物教 理案
第 25 章 玻尔的原子量子理论
一、经典理论对原子结构存在的困难 1. 氢原子光谱
2. 巴尔末系的里德伯公式(1885)
B
n2 n2
4
(n 3,4,5,6 )
B
——经验公式
~
1
R(
1 22
1 n2
)
(n 3,4,5,6, )
里德伯常数的实验值: R 4 1 096776107 m1
4 on22
me 2
n 1,2,3,
轨道是量子化的 5
rn
4 on22
me 2
n 1,2,3,
n 1 r1 0. 53 Å
-------第一玻尔轨道半径
其它可能的轨道:
rn n2r1 (r1 , 4r1 , 9r1 )
2)氢原子的能级
电子在半径为 rn 的轨道上运动时,原子系统的总能量是:
(2)对氢原子谱线的强度、宽度、偏振等问题遇到难以克服 的困难。
(3)沿用了经典物理的轨道等许多概念。
14
作业: 第 25 章——3,7,9
思 考(6、8、10)
独立认真完成作业 !
E Eek U
e2
8or
e2
8orn
能量量子化
将 rn 代入上式:
En
me4
802h2n2
(n 1,2,3 )
基态能量
n1 (第一玻尔轨道) E1 136eV
n1
En
136 n2
(eV )
( E1 ,
E1 4
,
E1 9
)
激发态
6
rn
4 on22
me2
En
me4
802h2n2
rn r1、4r1、9r1 n 1,2,3,
E1, E2, E3 En (E1 E2 E3 )
2) 跃迁假设:
kn
En
h
Ek
3) 轨道量子化条件:
L
n
n
h
2
3. 玻尔的氢原子理论:
mVr
En
Ek (n1,2, )
量子数
1)氢原子的轨道半径:
EmrVE2ek4Ue2or28e2or
L mVr n
E0
束缚态
r , E 0 原子电离
rn
(1) rn , En , R
(2)定态、频率跃迁的概念
(3)推出广义的巴尔末公式,预言了k=1,4,5的存在,
果然在1915——1924年间发现了这些谱线。 (4)对元素周期表能作一些解释
(5)在 k ,n 时,跃迁频率 v 与电子绕核运动
的频率相同(玻尔理论回到了经典理论)
2. 局限性 (1)对稍复杂的原子光谱,定性、定量都不能解释。
4. 结 合 能: 将动能为零的电子从无限远处移来和一个离 子结合成基态 的原子所放出的能量。数值上 等于最低能量的绝对值
5. 电 离 能:把某能级的电子搬到无限远处所需要的能 量。数值上等于状态能量的绝对值 12
例1:计算将动能为零的自由电子从无限远处移来和一个 氢离子结合成正常状态的氢原子所放出的能量。
E,r
原子半径为 1015 m 相矛盾 实际半径为 1010 m
2)原子发光的频率应等于电子运动的频率 电子运动轨道不断减小,速度大小不变 运动周期减小 频率增大 辐射光谱应是连续光谱
与实验相矛盾 3
二、玻尔的原子量子论
1.卢瑟福原子模型(原子的有核模型)
mv
原子的稳定性问题?
r
质疑:
原子分立的线状光谱?
玻尔:1911年秋、哥本哈根 剑桥 汤姆逊、 卢瑟福
普朗克、 爱因斯坦、 汉森
广义的巴尔末公式:
1922 Nobel Price
c
~
R(
1 k2
1 n2
)
11 Rc(k 2 n2 )
h
hRc k2
hRc n2
光子的能量 = 能量之差。 取不连续的值
1913‘哲学杂志’原子构造与分子构造 4
2. 玻尔原子系统的基本假设 1) 定态假设:原子处于一系列不连续稳定态。
9
5. 夫兰克—赫兹实验——验证原子系统定态能级存在
实验装置:
K极 电压V G极
加反向电压
G极
P极
实验结果:
阴极 栅极 板极
汞
蒸
A
K 气G P
V
300
200
(1)改变 V, V, Ek , I,
——到达P极的电子增加。
100
(2)V=4.9 v 后,I, 形成一峰值
(3)每隔V=4.9 v,就有峰值出现。