氢原子的玻尔理论知识
- 格式:ppt
- 大小:543.50 KB
- 文档页数:22


玻尔理论与氢原子跃迁一、基础知识 (一)玻尔理论1、定态:原子只能处于一系列不连续的能量状态中,在这些能量状态中原子是稳定的,电子虽然绕核运动,但并不向外辐射能量.2、跃迁:原子从一种定态跃迁到另一种定态时,它辐射或吸收一定频率的光子,光子的能量由这两个定态的能量差决定,即hν=Em -En.(h 是普朗克常量,h =6.63×10-34 J·s)3、轨道:原子的不同能量状态跟电子在不同的圆周轨道绕核运动相对应.原子的定态是不连续的,因此电子的可能轨道也是不连续的.4、氢原子的能级、能级公式 (1)氢原子的能级图(如图所示) (2)氢原子的能级和轨道半径 ①氢原子的能级公式:En =1n2E1(n =1,2,3,…),其中E1为基态能量,其数值为E1= -13.6 eV .②氢原子的半径公式:rn =n 2r1(n =1,2,3,…),其中r1为基态半径,又称玻尔半径,其数值为r1=0.53×10-10m.(二)氢原子能级及能级跃迁对原子跃迁条件的理解(1)原子从低能级向高能级跃迁,吸收一定能量的光子.只有当一个光子的能量满足hν=E 末-E 初时,才能被某一个原子吸收,使原子从低能级E 初向高能级E 末跃迁,而当光子能量hν大于或小于E 末-E 初时都不能被原子吸收.(2)原子从高能级向低能级跃迁,以光子的形式向外辐射能量,所辐射的光子能量恰等于发生跃迁时的两能级间的能量差.特别提醒 原子的总能量En =Ekn +Epn ,由ke2r2n =m v2rn 得Ekn =12ke2rn ,因此,Ekn 随r 的增大而减小,又En随n 的增大而增大,故Epn 随n 的增大而增大,电势能的变化也可以从电场力做功的角度进行判断,当r 减小时,电场力做正功,电势能减小,反之,电势能增大. 二、练习1、根据玻尔理论,下列说法正确的是( )A .电子绕核运动有加速度,就要向外辐射电磁波B .处于定态的原子,其电子绕核运动,但它并不向外辐射能量C .原子内电子的可能轨道是不连续的D .原子能级跃迁时,辐射或吸收光子的能量取决于两个轨道的能量差 答案 BCD解析 根据玻尔理论,电子绕核运动有加速度,但并不向外辐射能量,也不会向外辐射电磁波,故A 错误,B 正确.玻尔理论中的第二条假设,就是电子绕核运动可能的轨道半径是量子化的,不连续的,C 正确.原子在发生能级跃迁时,要放出或吸收一定频率的光子,光子能量取决于两个能级之差,故D 正确.2、下列说法中正确的是( )A .氢原子由较高能级跃迁到较低能级时,电子动能增加,原子势能减少B .原子核的衰变是原子核在其他粒子的轰击下而发生的C .β衰变所释放的电子是原子核内的中子转化成质子而产生的D .放射性元素的半衰期随温度和压强的变化而变化 答案 AC解析 原子核的衰变是自发进行的,选项B 错误;半衰期是放射性元素的固有特性,不 会随外部因素而改变,选项D 错误.3、(2000•安徽)根据玻尔理论,某原子的电子从能量为E 的轨道跃迁到能量为E'的轨道,辐射出波长为λ的光.以h 表示普朗克常量,C 表示真空中的光速,则E ′等于( C )A .E−h λ/cB .E+h λ/cC .E−h c /λD E+hc /λ4、欲使处于基态的氢原子激发,下列措施可行的是 A.用10.2 eV 的光子照射 B.用11 eV 的光子照射 C.用14 eV 的光子照射D.用11 eV 的光子碰撞[命题意图]:考查考生对玻尔原子模型的跃迁假设的理解能力及推理能力.[解答]:由"玻尔理论"的跃迁假设可知,氢原子在各能级间,只能吸收能量值刚好等于两能级之差的光子.由氢原子能级关系不难算出,10.2 eV 刚好为氢原子n=1和n=2的两能级之差,而11 eV 则不是氢原子基态和任一激发态的能量之差,因而氢原子只能吸收前者被激发,而不能吸收后者.对14 eV 的光子,其能量大于氢原子电离能,足可使“氢原子”电离,而不受氢原子能级间跃迁条件限制.由能的转化和守恒定律不难知道,氢原子吸收14 eV 的光子电离后产生的自由电子仍具有0.4 eV 的动能.另外,用电子去碰撞氢原子时,入射电子的动能可全部或部分地为氢原子吸收,所以只要入射电子的动能大于或等于基态和某个激发态能量之差,也可使氢原子激发,故正确选项为ACD.例1、一个具有E K0=20.40eV 动能、处于基态的氢原子与一个静止的、同样处于基态的氢原子发生对心碰撞(正碰),则下列关于处于基态的氢原子向激发态跃迁的说法中正确的是( ) A.不可能发生跃迁 B.可能跃迁到n=2的第一激发态 C.可能跃迁到n=3的第二激发态 D.可能跃迁到n=4的第三激发态【解析】两个氢原子做完全非弹性碰撞时损失的动能最大,损失动能的极值0110.22E E ev ∆==,所以处于基态的氢原子只可能跃迁到n=2的第一激发态。

高中物理:玻尔理论与氢原子的能级跃迁【知识点的认识】氢原子的能级和轨道半径(1)氢原子的能级公式:E n=E1(n=1,2,3,…),其中E1为基态能量E1=﹣13.6eV.(2)氢原子的半径公式:r n=n2r1(n=1,2,3,…),其中r1为基态半径,又称玻尔半径,r1=0.53×10﹣10m.(3)氢原子能级图(如图)①能级图中的横线表示氢原子可能的能量状态﹣﹣定态.②横线左端的数字“1、2、3…”表示量子数,右端的数字“﹣13.6,﹣3.4,…”表示氢原子的能级.③相邻横线间的距离,表示相邻的能级差,量子数越大,相邻的能级差越小.④带箭头的竖线表示原子由较高能级向较低能级跃迁,放出光子的能量:hν=E m﹣E n.特别提醒:能级越高,量子数越大,轨道半径越大,电子的动能越小,电势能越大,原子的能量随能级的升高而增大.【命题方向】题型一:氢原子能级跃迁问题氦原子被电离一个核外电子,形成类氢结构的氦离子.已知基态的氦离子能量为E1=﹣54.4eV,氦离子能级的示意图如图所示.在具有下列能量的光子中,不能被基态氦离子吸收而发生跃迁的是()A.40.8eV B.43.2eV C.51.0eV D.54.4eV分析:当光子的能量和某两个能级之间的能量差相等时才能被吸收,即体现能量的量子化.解答:根据量子理论可以知道,处于基态的离子在吸收光子能量时是成份吸收的,不能积累的.因此当其它能级和基态能量差和光子能量相等时,该光子才能被吸收.A、由能级示意图可知:第2能级和基态能级差为:△E1=E2﹣E1=﹣13.6﹣(﹣54.4)=40.8eV,故A选项中光子能量能被吸收,故A错误;B、没有能级之间的能量差和B中光子能量相等,故B正确;C、第4能级和基态能级差为:△E2=E4﹣E1=﹣3.4﹣(﹣54.4)=51.0eV;故C选项中光子能量能被吸收,故C错误;D、当光子能量大于等于基态能量时,将被处于基态离子吸收并能使其电离,故选项D中的光子能量能被吸收,故D错误故选B.点评:轨道量子化和能量量子化是量子力学的基础,是近代物理学的巨大飞跃,学生要能通过简单的计算理解其意义.【解题方法点拨】1.对原子跃迁条件的理解(1)原子从低能级向高能级跃迁,吸收一定能量的光子,当一个光子的能量满足hν=E末﹣E初时,才能被某一个原子吸收,使原子从低能级E初向高能级E末跃迁,而当光子能量hν大于或小于E末﹣E初时都不能被原子吸收.(2)原子从高能级向低能级跃迁,以光子的形式向外辐射能量,所辐射的光子能量恰等于发生跃迁时的两能级间的能量差.(3)原子跃迁条件hν=E m﹣E n只适用于光子和原子作用而使原子在各定态之间跃迁的情况.对于光子和处于基态的氢原子作用而使氢原子电离时,只要入射光子的能量E≥13.6eV,氢原子就能吸收.对于实物粒子与原子作用使原子激发时,粒子能量大于能级差即可.2.量子数为n的氢原子跃迁时辐射光子种数的判定方法:如果是一个氢原子,向低能级跃迁时辐射光子的可能频率种数为(n﹣1).如果是一群氢原子,向低能级跃迁时最多发出的光子种数为C.。






玻尔理论推导氢原子能级公式
氢原子的能级公式:en=1/n2e1(n=1,2,3,…),其中e1为基态能量。
氢原子能级:原子各个定态对应的能量是不连续的,这些能量值叫做能级。
在氢光谱中,
n=2,3,4,5,…...向n=1光子闪烁构成赖曼线系;
n=3,4,5,6……向n=2跃迁发光形成巴耳末线系;
n=4,5,6,7……向n=3光子闪烁构成帕邢线系;
n=5,6,7,8……向n=4跃迁发光形成布喇开线系,
其中只有巴耳末线系的前4条谱线落到红外线区域内。
能量最低的能级叫做基态,其他能级叫做激发态。
电子“远离”原子核,不再受原子核的吸引力时的状态叫做电离态,电离态的能级为0(电子由基态跃迁到电离态时,吸收的能量最大)。
能级光子首先由波尔(niels bohr)明确提出,但是波尔将宏观规律使用其中,所以除了氢原子的能级光子之外,在对其他繁杂的原子的光子规律的探究中,波尔碰到了非常大的困难。
组成物质的原子中,有不同数量的粒子(电子)分布在不同的能级上,在高能级上的粒子受到某种光子的激发,会从高能级跳到(跃迁)到低能级上,这时将会辐射出与激发它的光相同性质的光。

高中物理玻尔氢原子模型玻尔氢原子模型是由丹麦物理学家尼尔斯·玻尔在1913年提出的一种原子模型,它是描述氢原子中电子的位置和能量的理论。
这是一种经典的模型,不考虑量子力学的影响,但它对于许多实验观测提供了相当准确的预测,是量子力学的发展过程中的基础。
氢原子由一个质子和一个电子组成,质子带正电荷,电子带负电荷。
玻尔氢原子模型假设电子在原子的轨道上旋转,并且仅在一些特定的轨道上旋转,这些轨道的能量是确定的。
电子可以从一条轨道跳到另一条轨道上,跳跃的过程中吸收或释放能量。
玻尔氢原子模型通过量子条件和量子化概念将原子轨道和轨道能量的分立现象引入了物理学中。
在玻尔氢原子模型中,每个轨道都有一定的能量,电子在轨道间跳跃时,它所接受或放出的能量是一个确定的值,这个值正好等于两个轨道的能量差。
量子条件是指只有某些特定的轨道能够存在于氢原子中,其他的轨道是不可能存在的。
这些特定的能量被称为能级,它们对应着不同的轨道。
玻尔氢原子模型中能级是通过以下公式计算得出的:E=-\frac{13.6\textrm{ eV}}{n^2}其中E是能级,n是一个整数,称为主量子数。
随着n的增加,能量越来越小。
因此,当电子从一个能级向低能级跳跃时,会放出能量,当它从低能级向高能级跳跃时,会吸收能量。
在一个稳定的氢原子中,电子会停留在最低能级(n=1)上。
当外界施加能量时,电子就可以从这个能级跃迁到更高的能级,这个过程被称为激发(excitation)。
当电子回到最低能级时,它会释放出能量,这个过程被称为放射(emission),通常以光的形式显示出来。
总之,玻尔氢原子模型提供了一种经典的理论框架来解释氢原子的行为。
虽然它并不是完全准确的,但它为量子力学的研究奠定了基础,并帮助科学家更好地理解了原子的结构和性质。
玻尔的氢原子理论:原子只能处在一系列具有不连续能量的稳定状态,简称定态。
定态时,核外电子在一定的轨道上作圆周运动,不辐射电磁波.: 原子从一个定态跃迁到另一个定态时,会辐射或吸收一个能量为h 的光子.1. 定态假设n k E E h2.频率假设n kE E 一、玻尔的氢原子理论的三个基本假设...3 ,2 ,1π2 n n hn r m Lv 3.轨道角动量量子化假设n 称为轨道量子数称为约化普朗克常量2h第n 个定态电子的轨道半径为:玻尔半径二、氢原子轨道半径和能量的计算库仑力=向心力v nE n +e-e m m p r n 角动量量子化条件(1)(2)运动轨道是量子化的23...n ,,对应的定态分别称为第一激发态、第二激发态……n=1对应的定态称为基态能量量子化夫兰克-赫兹实验证实了原子能级的存在121E (n 1,2,3,)n基态能量meE .eV h412201368不连续的分立能量称为能级(3)(1)1122211n n (n )E E E E n (n )n E:n 三、对应原理这符合玻尔的对应原理n n r ,E 0,E 0电子能量趋于连续。
,n 对应原理:在极限条件下,新理论应与旧理论形式一致。
新理论应包含一定经验范围内证明是正确的旧理论。
在量子数n 很大时,玻尔氢原子理论应与经典理论一致。
四、玻尔氢原子理论值和实验值比较原因在于原理论假设氢核静止; 而实际核与电子一起绕它们的质心旋转,这时应用折合质量μ代替mn k E E νh423220me 118h k n-(1)42322111=()8 0νme νλc εh c k n2211=R()() n k k n (2)赖曼系k=1巴耳末系k=2氢原子能级图0n kh E E 光子能量:-13.6-1.51-3.39E n (eV)n = 1n = 2n = 3n = 4n = 5n = 6n 213.6E -eVn根学派的领头人。
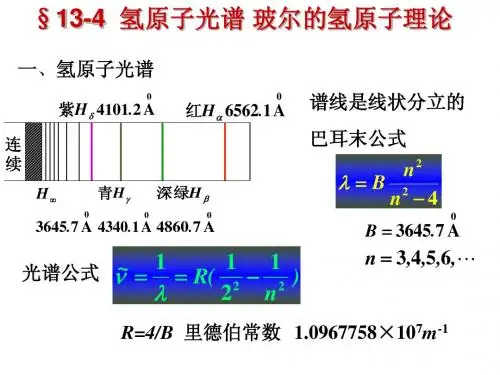
第二章 原子的能级和辐射一、学习要点:1.氢原子光谱:线状谱、五个线系(记住名称、顺序)、广义巴尔末公式)11(~22nm R -=ν、 光谱项()2nR n T =、并合原则:)()(~n T m T -=ν 2.玻尔氢原子理论:(1)玻尔三条基本假设的实验基础和内容(记熟)(2)圆轨道理论(会推导):氢原子中假设原子核静止,电子绕核作匀速率圆周运动02200202220A 529,04,Z Z 4≈===e m a n a n e m r e e n πεπε;13714,Z Z 40202≈===c e n c n e c e n πεααπευ; ()n hcT n hc R n e m E e n --=-=∞22224220Z 2Z )41( πε,n =1.2.3……(3)实验验证:(a )氢原子五个线系的形成)11(Z ~,)4(222232042n m R c h e m R e -==∞∞νπεπ (会推导)非量子化轨道跃迁 )(212n E E mv h -+=∞ν (b )夫-赫实验:装置、.结果及分析;原子的电离电势、激发电势3.类氢离子(+++Li ,He ,正电子偶素.-μ原子等) (1) He +光谱:毕克林系的发现、波数公式、与氢原子巴耳末系的异同等(2)理论处理(会推导):计及原子核的运动,电子和原子核绕共同质心作匀速率圆周运动e e m M m M +⋅=μ, 正负电荷中心之距Ze n r n 22204μπε =. 能量2242202Z )41(n e E n μπε-=,里德伯常数变化Mm R R e A +=∞11 重氢(氘)的发现4.椭圆轨道理论 索末菲量子化条件q q n h n pdq ,⎰=为整数a n nb n e m a n e m E n p e n ϕϕϕπεπε==-==,Z 4,2Z )41(,2220224220 ,n n n ,,3,2,1;,3,2,1 ==ϕn 一定,n E 一定,长半轴一定,有n 个短半轴,有n 个椭圆轨道(状态),即n E 为n 度简并。