工程数学 - 作业 - 实验(05)北工大 - 软件学院
- 格式:docx
- 大小:44.78 KB
- 文档页数:11

实验五解:依据题意“总的停车距离=反应距离+刹车距离”,设L表示跟车距离,s表示刹车距离,v表示车速,t表示反应时间,即:L=vt+s用平方和最小方法估计系数s、t:min s,ts+v i t−L i2 ni=1将50组实验数据代入计算并取最优解,相应的LINGO程序如下图1-1所示:图1-1(详细如下)model:sets:quantity/1..50/:v,L;endsetsdata:v= 4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 15 16 16 17 17 17 18 18 18 18 19 19 19 20 20 20 20 20 22 23 24 24 24 24 25;L= 2 10 4 22 16 10 18 26 34 17 28 14 20 24 28 26 34 34 46 26 36 60 80 20 26 54 32 40 32 40 50 42 56 76 84 36 46 68 32 48 52 56 64 66 54 70 92 93 120 85;enddatamin=@sum(quantity:(s+v*t-L)^2);@free(s);@free(t);endLINGO程序计算结果截取如下图1-2所示:图1-2由计算结果可知:平方和最小时,s=-17.57909,t=3.932409。
即,L=3.932409v−17.57909解:依据题意设第一个作业点为坐标原点,即(0, 0)点。
则第二个作业点的坐标为(75,330),第三个作业点的坐标为(-225, -40)。
设两个临时机场的位置坐标分别为A x a,y a、B x b,y b,A机场给三个作业点提供的油料分别为a1、a2、a3,B机场给三个作业点提供的油料分别为b1、b2、b3,要求每月从机场到作业点的吨公里数最少,建立数学模型:目标函数为:Min L=a1x a2+y a2+b1x b2+y b2+a2x a−752+y a−3302+b2x b−752+y b−3302+a3x a+2252+y a+402+b3x b+2252+y b+402约束条件为:a1+b1=25a2+b2=14a3+b3=34相应的LINGO程序如下图2-1所示:图2-1(不是很清晰,详细见下)min=a1*(xa^2+ya^2)^0.5+b1*(xb^2+yb^2)^0.5+a2*((xa-75)^2+(ya-330)^2)^0 .5+b2*((xb-75)^2+(yb-330)^2)^0.5+a3*((xa+225)^2+(ya+40)^2)^0.5+b3*((x b+225)^2+(yb+40)^2)^0.5;a1+b1=25;a2+b2=14;a3+b3=34;@free(xa);@free(xb);@free(ya);@free(yb);LINGO程序运行结果如下图2-2所示:图2-2由计算结果可知:临时机场A建立的位置坐标为(0, 0)处,机场B建立的位置坐标为(-225,-40)处时,并且A机场给第1个作业点提供油料25t,给第2个作业点提供14t,给第3个作业点提供0t;机场B给第1个作业点提供0t,给第2个作业点提供0t,给第三个作业点提供34t,这种方案下每月的吨公里数最少为4737.816。

2微分方程实验1、微分方程稳定性分析绘出下列自治系统相应的轨线,并标出随 t 增加的运动方向,确定平■衡点, 并按稳定的、渐近稳定的、或不稳定的进行分类:解:(1)由 f (x ) =x=0, f (y ) =y=0;可得平衡点为(0,0),___ 1 0系数矩阵A,求得特征值入1=1,入2=1;0 1p=-(入1+入2)=-2<0 , q=入1入2=1>0;对照稳定性的情况表,可知平■衡点(0, 0) 是不稳定的。
图形如下:(2)如上题可求得平衡点为(0,0 ),特征值入1=-1,入2=2;p=-(入1+入2)=-1<0 , q-入1入2=-2<0;对照稳定性的情况表,可知平■衡点(0, 0) 是不稳定的。
其图形如下:dx⑴dt dtx, y;dxdtdydt dx x, ⑶尸 2y ;晋 dx y, (4) ? 2x;也 dtx+1, 2y.(3) 如上题可求得平■衡点为(0,0 ),特征值入1=0 + 1.4142i,入2=0 -1.4142i; p=-(入1+入2)= 0, q-入1入2=1.4142>0;对照稳定性的情况表,可知平■衡点(0, 0)是不稳定的。
其图形如下:(4) 如上题可求得平衡点为(1,0 ),特征值入1=-1,入2=-2;p=-(入1+入2)= 3>0, q=入1入2=2>0;对照稳定性的情况表,可知平■衡点(1, 0) 是稳定的。
其图形如下:2、种群增长模型一个片子上的一群病菌趋向丁繁殖成一个圆菌落.设病菌的数目为N,单位成员的增长率为r1,则由Malthus生长律有竺r1 N,但是,处丁周界表面的dt那些病菌由丁寒冷而受到损伤,它们死亡的数量与N2成比例,其比例系数为r2, 求N满足的微分方程.不用求解,图示其解族.方程是否有平衡解,如果有,是否为稳定的?解:由题意很容易列出N满足的微分方程:坐r1N r2N; f(N)dt令f(N)=O,可求得方程的两个平■衡点N1=0,N2=「22/r i21 1d2N 1 5 52 (r1 r2N 2) (r1N r2N 2)dt 2进而求得A d2N 令r dt2 2 0可求得N=r2 /4r〔则N=N1 N=N2 N=r22/4r i2可以把第一象限划为三部分,且从下到上三部分中分0,冬dt2.2 2 c dN cdN c dN cdN 0, ;—0, —r 0; —0, ―rdt dt dt dt则可以画出N (t) 的图形,即微分方程的解族,如下图所示:由图形也可以看出,对丁方程的两个平■衡点,其中N1=0是不稳定的;N2=^2 /「;是稳定的o3、有限资源竞争模型1926年Volterra 提出了两个物种为共同的、有限的食物来源而竞争的模型当[b MX h 2X 2)]x dt dX2 电 2(h i X i h 2X 2)]X 2dt假设也 坦,称垣为物种i 对食物不足的敏感度,(1) 证明当x1(t0)>0时,物种2最终要灭亡; (2) 用图形分析方法来说明物种 2最终要灭亡.解:(1)由上述方程组 f (x1) =[b 1〔S' h 2x 2)]x 1=0,f (x2)=电2 (h 1X 1h 2X 2)]X 2=0,可得方程的平■衡点为R (0,0), P 1 (E,0),P 2 (0, M).2 h 2对平衡点P 。


1.曲线拟合有关部门希望研究车速与刹车距离之间的关系, y=β0+β1x ,其中x 为车速,y 为刹车距离,现测得50组数据(xi ,yi )(i=1,2,3…,50)(见表3.1,用三种方法((1)平方和最小;(2)绝对偏差和最小; (3)最大偏差最小)估计系数β0和β1,并分析三种方法的计算效果(注:用LINGO 软件求解,用其他软件画出散点图和回归直线),说明哪一种方法得到有结果更合理. 解:(1)平方和最小,根据最小二乘方法求解,相应的无约束问题为()2n1i i i 10y -x min 10∑=+=ββββ,,为了方便计算,将β0, β1换成A,B ,相应的LINGO程序如下: sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@sum (quantity: (A+B*x-y)^2); @free (A); @free(B);计算结果如图所示用LINGO解得:A= -17.57909,B=3.932409,所以y= -17.57909+3.932409*x. β0= -17.57909,β1=3.932409(2)绝对偏差和最小,根据最小一乘方法求解,相应的无约束问题为∑=+=ni1ii1y-xmin1ββββ,,为了方便计算,将β0, β1换成A,B,相应的LINGO程序如下:sets:quantity/1..50/: x,y;endsetsdata:y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,4 0,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17, 17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25;enddatamin=@sum(quantity: @abs(A+B*x-y));@free(A); @free(B);计算结果如图所示用LINGO 解得:A= -11.6,B=3.4, 所以y= -11.6+3.4*x. β0= -11.6,β1=3.4(3)最大偏差最小,根据最大偏差的最小的方法求解,相应的无约束问题为i i 101y -x max min 10ββββ+=≤≤ni ,,为了方便计算,将β0, β1换成A,B ,相应的LINGO程序如下: sets :quantity/1..50/: x,y; endsets data :y=2,10,4,22,16,10,18,26,34,17,28,14,20,24,28,26,34,34,46,26,36,60,80,20,26,54,32,40,32,40,50,42,56,76,84,36,46,68,32,48,52,56,64,66,54,70,92,93,120,85;x=4,4,7,7,8,9,10,10,10,11,11,12,12,12,12,13,13,13,13,14,14,14,14,15,15,15,16,16,17,17,17,18,18,18,18,19,19,19,20,20,20,20,20,22,23,24,24,24,24,25; enddatamin =@max (quantity: @abs (A+B*x-y)); @free (A); @free (B); 计算结果如图所示用LINGO解得:A= -12,B=4,所以y= -12+4*x. β0= -12,β1=4X轴为速度,Y轴为距离,蓝色点多已知数据点,y1,y2,y3分别为前三种方法求得的数据点,黑色线为通过蓝色数据点得到的线性回归方程y=1.445x+6.121,比较三种方法得到曲线,可以看到与红色曲线吻合度高于其他两种方法,所以第一种方法得到的结果更为合理。
综合实验报告第一部分:用线性表来接收学生信息。
排序用冒泡排序。
主要变量名:SQLISTTP v;主要函数名:SetupAddDeleteFindOrder,无接口,设置v为全局变量。
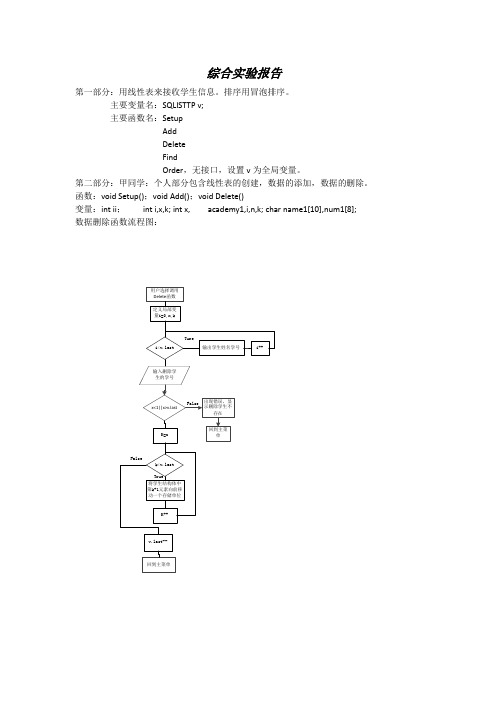
第二部分:甲同学:个人部分包含线性表的创建,数据的添加,数据的删除。
函数:void Setup();void Add();void Delete()变量:int ii;int i,x,k; int x, academy1,i,n,k; char name1[10],num1[8];数据删除函数流程图:第三部分:乙同学:管理系统包括线性表的排序和查询功能。
void Find()void Order()数据查询功能流程图:第四部分:创建—1插入—2删除—3查询—4排序—5退出—61<回车>请输入你要建立数据的人数3<回车>请输入第1位的姓名shuyufan<回车>请输入第1位的性别(MorF) M<回车>请输入第1位的学号11021114<回车>请输入第1位的学院(1-15) 1<回车>输入最近5次的消费明细1 1 1 1 1<回车>请输入第2位的姓名zhaoyu<回车>请输入第2位的性别(MorF) M<回车>请输入第2位的学号11021111<回车>请输入第2位的学院(1-15) 1<回车>输入最近5次的消费明细1 2 3 4 5<回车>请输入第3位的姓名wangchao<回车>请输入第3位的性别(MorF) F<回车>请输入第3位的学号11021201<回车>请输入第3位的学院(1-15) 2<回车>输入最近5次的消费明细0 0 0 0 0<回车><回车>创建—1插入—2删除—3查询—4排序—5退出—64<回车>请选择你想要查询的方式:1—姓名查找2—学号查找3—学院查找1<回车>请输入你要查询的姓名shuyufan<回车>name:shuyufansex:Mnum:11021114academy:1最近5次消费记录:1 1 1 1 1<回车> 2<回车>请输入第4位的姓名wuweijia<回车>请输入第4位的性别(MorF)F<回车>请输入第4位的学号11021108<回车>请输入第4位的学院(1-15)1<回车>输入最近5次的消费明细5 4 3 2 1<回车><回车>创建—1插入—2删除—3查询—4排序—5退出—64<回车>请选择你想要查询的方式:1—姓名查找2—学号查找3—学院查找2<回车>请输入你要查询的学号11021108<回车>name:wuweijiasex:Fnum:11021108academy:1最近5次消费记录:5 4 3 2 1<回车>创建—1插入—2删除—3查询—4排序—5退出—64<回车>请选择你想要查询的方式:1—姓名查找2—学号查找3—学院查找3<回车>2<回车>name:wangchaosex:Fnum:11021201academy:2最近5次消费记录:0 0 0 0 0<回车>3<回车>1:姓名:shuyufan 学号:110211141:姓名:zhaoyu 学号:110211111:姓名:wangchao 学号:110212011:姓名:wuweijia 学号:11021108输入你想要删除的编号2<回车><回车>5<回车>num:11021108 name:wuweijia sex:F academy:1num:11021114 name:shuyufan sex:M academy:1num:11021201 name:wangchao sex:F academy:2<回车>6<回车>请按任意键继续. . .<回车>结论:测试结果与预期一样,完成了预期的创建,插入,删除,查询,排序,退出效果。

最优化与存储模型实验作业一、 基本实验1.拟合问题有关部门希望研究车速与刹车距离之间的关系,01y x ββ=+,其中x 为车速,y 为刹车距离,现测得50组数据(,)(1,2,,50)i i x y i =(见表5.1),用三种方法((1)平方和最小;(2)绝对偏差和最小;(3)最大偏差最小)估计系数0β,1β,并分析三种方法的计算效果(注:用Lingo 软件求解,用其他软件画出散点图和回归直线),说明那一种方法得到的结果更合理。
解:x 为车速,y 为刹车距离,(1)平方和最小;(2)绝对偏差和最小;(3)最大偏差最小。
三种情况下相应的无约束问题为:01010150210,15010,110,150min (),min ,min max ,i i i i i i i i i z x y z x y z x y ββββββββββββ==≤≤=+-=+-=+-∑∑编写相应的Lingo 程序分别为(由于β和α在程序中不好体现,我们仍然用a表示α,b表示β):(1)平方和最小:sets:Quantity/1..50/: x, y;endsetsdata:x=4, 4, 7, 7, 8, 9, 10, 10, 10, 11, 11, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14,15, 15, 15, 16, 16, 17, 17, 17, 18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 22,23, 24, 24, 24, 24, 25;y=2, 10, 4, 22, 16, 10, 18, 26, 34, 17, 28, 14, 20, 24, 28, 26, 34, 34, 46, 26, 36 ,60, 80, 20, 26, 54, 32, 40, 32, 40, 50, 42, 56, 76, 84, 36, 46, 68, 32, 48, 52, 56, 64, 66, 54, 70, 92, 93, 120, 85;enddataMin=@sum(quantity: (a*x+b-y)^2);@free(a);@free(b);运行结果见xueyunqiang-chapter5-1所以拟合结果是:=-y x3.93240917.57909(2)绝对偏差和最小:编写Lingo程序:sets:Quantity/1..50/: x, y;endsetsdata:x=4, 4, 7, 7, 8, 9, 10, 10, 10, 11, 11, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14, 15, 15, 15, 16, 16, 17, 17, 17, 18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 22, 23, 24, 24, 24, 24, 25;y=2, 10, 4, 22, 16, 10, 18, 26, 34, 17, 28, 14, 20, 24, 28, 26, 34, 34, 46, 26, 36 ,60, 80, 20, 26, 54, 32, 40, 32, 40, 50, 42, 56, 76, 84, 36, 46, 68, 32, 48, 52, 56, 64, 66, 54, 70, 92, 93, 120, 85;enddataMin=@sum (quantity: @abs(a*x+b-y));@free(a); @free(b);运行结果见xueyunqiang-chapter5-1(2)所以拟合结果为;y x=-3.411.6,(3)最大偏差最小:编写Lingo程序:sets:Quantity/1..50/: x, y;endsetsdata:x=4, 4, 7, 7, 8, 9, 10, 10, 10, 11, 11, 12, 12, 12, 12, 13, 13, 13, 13, 14, 14, 14, 14,15, 15, 15, 16, 16, 17, 17, 17, 18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 22,23, 24, 24, 24, 24, 25;y=2, 10, 4, 22, 16, 10, 18, 26, 34, 17, 28, 14, 20, 24, 28, 26, 34, 34, 46, 26, 36 ,60, 80, 20, 26, 54, 32, 40, 32, 40, 50, 42, 56, 76, 84, 36, 46, 68, 32, 48, 52, 56, 64, 66, 54, 70, 92, 93, 120, 85;enddataMin=@max (quantity: @abs(a*x+b-y));@free(a); @free(b);运算结果见xueyunqiang-chapter5-1(3)所以拟合结果为:=-412,y x三种拟合结果为:(1) 3.93240917.57909=-y x(2) 3.411.6,=-y x(3)412,=-y x在Matlab中绘制散点图和拟合直线图如下:>>x=[4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 1314 14 14 14 15 15 15 16 16 17 17 17 18 18 18 18 19 19 1920 20 20 20 20 22 23 24 24 24 24 25];>>y=[2 10 4 22 16 10 18 26 34 17 28 14 20 24 28 26 34 34 4626 36 60 80 20 26 54 32 40 32 40 50 42 56 76 84 36 46 6832 48 52 56 64 66 54 70 92 93 120 85];>> plot(x,y,'s')>> hold on>> x=0:0.05:25;y=3.932409*x-17.57909;plot(x,y,'b');>> hold on;>> x=0:0.05:25;y=3.4*x-11.6;plot(x,y,'r-');>> hold on;>> x=0:0.05:25;y=4*x-12;plot(x,y,'m- -');由散点图可知最上角的点明显异于其他点,最大偏差最小回归直线受最大偏差影响明显,最小二乘统计性质较好,但是受异常点的影响,也有向上偏移的趋势,而最小一乘受异常点影响的程度较小,基本上在主流数据之间。
北方工业大学计算机图形学课程实验报告题目:实验二几何变换学院:专业:指导教师:学生班级:学生学号:学生姓名:教师评定:学号:班级:姓名:实验报告二几何变换实验一.实验目的1.熟悉OpenGL图形库;2.掌握几何变换算法。
二.实验环境1.软件环境:操作系统:Win7应用软件:VC6.0,OpenGL2.硬件环境CPU:显卡:三.用矩阵计算实现二维几何变换写程序实现基本矩阵运算,同时实现平移、放缩、旋转等几何变换。
要求自己设计实例验证平移、放缩、旋转函数,采用键盘交互。
已给出二维点坐标结构体、单位矩阵赋值函数。
已给出:二维点坐标结构体struct Point2D{float x, y;}已给出:宏定义3×3数组typedef float Matrix3x3 [3][3];Matrix3x3 matComposite;已给出:单位矩阵赋值函数void matrix3x3SetIdentity(Matrix3x3 matIdent3x3){int row, col;for(row=0; row<3;row++){for(col=0; col<3; col++){matIdent3x3[row][col] = (row==col);}}}要求给出以下函数及实例截图。
1.矩阵左乘运算函数Void matrix3x3PreMultiply(Matrix3x3 m1, Matrix3x3 m2){int row, col;Matrix3x3 temp;for(row=0; row<3;row++){for(col=0; col<3; col++){temp[row][col] = m1[row][0]*m2[0][col] +m1[row][1]*m2[1][col] + m1[row][2]*m2[2][col];}}for(row=0; row<3;row++){for(col=0; col<3; col++){m2[row][col]=temp[row][col];}}2.平移函数void Translate2D (float tx, float ty){Matrix3x3 matTransl;matrix3x3SetIdentity (matTransl);matTransl[0][2]=tx;matTransl[1][2]=ty;matrix3x3PreMultiply(matTransl,matComposite);}3.顶点矩阵左乘合成函数void TransformVerts2D(int nVerts,Point2D * verts){GLint k;GLfloat temp1, temp2;for (k=0;k<nV erts; k++){temp1=matComposite [0][0]*verts[k].x + matComposite[0][1]*verts[k].y + matComposite [0][2];temp2=matComposite [1][0]*verts[k].x + matComposite[1][1]*verts[k].y+matComposite [1][2];verts[k].x=temp1;verts[k].y=temp2;}}4.绘制三角形函数void RenderTriangle (Point2D* verts){int k;glBegin (GL_TRIANGLES);for (k=0;k<3;k++){glVertex2f(verts[k].x,verts[k].y);}glEnd();}5.旋转函数void Rotate2D (Point2D fixedPt, float theta){Matrix3x3 matRot;matrix3x3SetIdentity (matRot);matRot [0][0]=cos(theta);matRot [0][1]=-sin (theta);matRot [0][2]=fixedPt.x*(1-cos (theta))+fixedPt.y*sin(theta);matRot [1][0]=sin (theta);matRot [1][1]=cos (theta);matRot [31][2]=fixedPt.x*(1-cos (theta))-fixedPt.y*sin(theta);matrix3x3PreMultiply(matRot,matComposite);}6.缩放函数void scale2D (GLfloat sx,GLfloat sy,wcPt2D fixedPt){ Matrix3x3 matScale;matrix3x3SetIdentity(matScale);matScale [0][0]=sx;matScale [0][2]=(1-sx)*fixedPt.x;matScale [1][1]=sy;matScale [1][2]=(1-sy)*fixedPt.y;matrix3x3PreMultiply(matScale,matComposite); }7.平移实例及截图8.旋转实例及截图9.缩放实例及截图四.用OpenGL函数库实现几何图元旋转特效在Nehe教程Lesson04基础上,修改程序,在屏幕上画两个三角形、两个四边形,并完成相应动画效果,三角形A绕X轴旋转,三角形B绕Y轴旋转,四边形C绕Z轴旋转,四边形D绕X轴旋转。
北京工业大学最优化基础实验:使用matlab 求解规划问题 实验一非线性最优化方法实验1.042:.844)(min )21212221≤-++--+=x x t s x x x x x f a解:>> f=@(x)x(1)^2+x(2)^2-4*x(1)-4*x(2)+8;>> A=[1,2]b=[4]A =1 2b =4>> [x,fval]=fmincon(f,[10,10],A,b)x =1.6000 1.2000fval =0.80002.)()(min 321232221642x x x x x x x f ++-++= 解:>> apple=@(x)x(1)^2+x(2)^2+x(3)^2-(2*x(1)+4*x(2)+6*x(3))apple =@(x)x(1)^2+x(2)^2+x(3)^2-(2*x(1)+4*x(2)+6*x(3))>> [x,fval]=fminunc(apple,[1,1,4])Warning: Gradient must be provided for trust-region algorithm; using line-search algorithm instead.> In fminunc at 341Local minimum found.Optimization completed because the size of the gradient is less than the default value of the function tolerance.<stopping criteria details>x =1.00002.00003.0000fval =-143.,0 )1(:.)( min)2 12311≥≥--=x xx xt sx xfc解>> f3=@(x)x(1) f3 =@(x)x(1) >>lb=zeros(2,1) lb =>>x0=[1,1]x0 =1 1>> [x,optimal]=fmincon(@objfun,x0,[],[],[],[],lb,[],@nonlcon)Active inequalities (to within options.TolCon = 1e-006): lower upper ineqlinineqnonlin12x =0 0optimal =4.,04:.)3()3()(min)2 1212221≥≥---+-=x xx xt sxxxfd>> f4=@(x)(x(1)-3)^2+(x(2)-3)^2 f4 =@(x)(x(1)-3)^2+(x(2)-3)^2 >> A=[1,1]A =1 1>> b=[4]b =4>>lb=zeros(2,1)lb =>> [x,fval]=fmincon(f4,[10,10],A,b,[],[],lb,[])Warning: Trust-region-reflective algorithm does not solve this type of problem, using active-set algorithm. You could also trythe interior-point or sqp algorithms: set the Algorithm option to 'interior-point' or 'sqp' and rerun. For more help, seeChoosing the Algorithm in the documentation.> In fmincon at 472Local minimum found that satisfies the constraints.Optimization completed because the objective function is non-decreasing infeasible directions, to within the default value of the function tolerance,and constraints are satisfied to within the default value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-006):lower upper ineqlinineqnonlin1x =2.0000 2.0000fval =2.00005.6:.)2()2()(min)212221=-+-+-=xxt sx xxfe本题要求输出寻优过程的迭代次数。
工程数学作业(第一次)(满分100分)第2章 矩阵(一)单项选择题(每题2分,共20分)⒈设a a a b b b c c c 1231231232=,则a a a a b a b a b c c c 123112233123232323---=( ).A. 4B. -4C. 6D. -6⒉若000100002001001a a=,则a =( ).A.12 B. -1 C. -12D. 1 ⒊乘积矩阵1124103521-⎡⎣⎢⎤⎦⎥-⎡⎣⎢⎤⎦⎥中元素c 23=( ). A. 1 B. 7 C. 10 D. 8⒋设A B ,均为n 阶可逆矩阵,则下列运算关系对旳旳是( ). A. A BAB +=+---111 B. ()AB BA --=11C. ()A B A B +=+---111 D. ()AB A B ---=111⒌设A B ,均为n 阶方阵,k >0且k ≠1,则下列等式对旳旳是( ). A. A B A B +=+ B. AB n A B =C. kA k A =D. -=-kA k A n()⒍下列结论对旳旳是( ).A. 若A 是正交矩阵,则A -1也是正交矩阵B. 若A B ,均为n 阶对称矩阵,则AB 也是对称矩阵C. 若A B ,均为n 阶非零矩阵,则AB 也是非零矩阵D. 若A B ,均为n 阶非零矩阵,则AB ≠0⒎矩阵1325⎡⎣⎢⎤⎦⎥旳伴随矩阵为( ). A. 1325--⎡⎣⎢⎤⎦⎥ B.--⎡⎣⎢⎤⎦⎥1325 C. 5321--⎡⎣⎢⎤⎦⎥ D. --⎡⎣⎢⎤⎦⎥5321⒏方阵A 可逆旳充足必要条件是( ).A.A ≠0B.A ≠0C. A *≠0D. A *>0 ⒐设A B C ,,均为n 阶可逆矩阵,则()ACB '=-1( ).A. ()'---B A C 111 B. '--B C A 11C. A C B ---'111() D. ()B C A ---'111⒑设A B C ,,均为n 阶可逆矩阵,则下列等式成立旳是( ). A. ()A B A AB B +=++2222 B. ()A B B BA B +=+2C. ()221111ABC C B A ----= D. ()22ABC C B A '='''(二)填空题(每题2分,共20分)⒈21014001---= . ⒉---11111111x 是有关x 旳一种一次多项式,则该多项式一次项旳系数是 . ⒊若A 为34⨯矩阵,B 为25⨯矩阵,切乘积AC B ''故意义,则C 为 矩阵.⒋二阶矩阵A =⎡⎣⎢⎤⎦⎥=11015.⒌设A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=--⎡⎣⎢⎤⎦⎥124034120314,,则()A B +''= . ⒍设A B ,均为3阶矩阵,且A B ==-3,则-=2AB .⒎设A B ,均为3阶矩阵,且A B =-=-13,,则-'=-312()A B .⒏若A a =⎡⎣⎢⎤⎦⎥101为正交矩阵,则a = . ⒐矩阵212402033--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥旳秩为 . ⒑设A A 12,是两个可逆矩阵,则A O OA 121⎡⎣⎢⎤⎦⎥=- .(三)解答题(每题8分,共48分)⒈设A B C =-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥123511435431,,,求⑴A B +;⑵A C +;⑶23A C +;⑷A B +5;⑸AB ;⑹()AB C '.⒉设A B C =--⎡⎣⎢⎤⎦⎥=-⎡⎣⎢⎤⎦⎥=--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥121012103211114321002,,,求AC BC +.⒊已知A B =-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=-⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥310121342102111211,,求满足方程32A X B -=中旳X . ⒋写出4阶行列式1020143602533110--中元素a a 4142,旳代数余子式,并求其值. ⒌用初等行变换求下列矩阵旳逆矩阵:⑴ 122212221--⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥; ⑵ 1234231211111026---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥; ⑶1000110011101111⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥.⒍求矩阵1011011110110010121012113201⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥旳秩.(四)证明题(每题4分,共12分)⒎对任意方阵A ,试证A A +'是对称矩阵.⒏若A 是n 阶方阵,且AA I '=,试证A =1或-1. ⒐若A 是正交矩阵,试证'A 也是正交矩阵.工程数学作业(第二次)(满分100分)第3章 线性方程组(一)单项选择题(每题2分,共16分)⒈用消元法得x x x x x x 12323324102+-=+=-=⎧⎨⎪⎩⎪旳解x x x 123⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥为( ).A. [,,]102-'B. [,,]--'722C. [,,]--'1122D. [,,]---'1122⒉线性方程组x x x x x x x 12313232326334++=-=-+=⎧⎨⎪⎩⎪( ). A. 有无穷多解 B. 有唯一解 C. 无解 D. 只有零解⒊向量组100010001121304⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥,,,,旳秩为( ). A. 3 B. 2 C. 4 D. 5⒋设向量组为αααα12341100001110101111=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥,,,,则( )是极大无关组.A. αα12,B. ααα123,,C. ααα124,,D. α1⒌A 与A 分别代表一种线性方程组旳系数矩阵和增广矩阵,若这个方程组无解,则( ). A. 秩()A =秩()A B. 秩()A <秩()A C. 秩()A >秩()A D. 秩()A =秩()A -1⒍若某个线性方程组对应旳齐次线性方程组只有零解,则该线性方程组( ). A. 也许无解 B. 有唯一解 C. 有无穷多解 D. 无解 ⒎如下结论对旳旳是( ).A. 方程个数不不小于未知量个数旳线性方程组一定有解B. 方程个数等于未知量个数旳线性方程组一定有唯一解C. 方程个数不小于未知量个数旳线性方程组一定有无穷多解D. 齐次线性方程组一定有解⒏若向量组ααα12,,, s 线性有关,则向量组内( )可被该向量组内其他向量线性表出.A. 至少有一种向量B. 没有一种向量C. 至多有一种向量D. 任何一种向量(二)填空题(每题2分,共16分)⒈当λ= 时,齐次线性方程组x x x x 121200+=+=⎧⎨⎩λ有非零解.⒉向量组[][]αα12000111==,,,,,线性 .⒊向量组[][][][]123120100000,,,,,,,,,,,旳秩是 .⒋设齐次线性方程组ααα1122330x x x ++=旳系数行列式ααα1230=,则这个方程组有 解,且系数列向量ααα123,,是线性 旳.⒌向量组[][][]ααα123100100===,,,,,旳极大线性无关组是 . ⒍向量组ααα12,,, s 旳秩与矩阵[]ααα12,,, s 旳秩 .⒎设线性方程组AX =0中有5个未知量,且秩()A =3,则其基础解系中线性无关旳解向量有 个.⒏设线性方程组AX b =有解,X 0是它旳一种特解,且AX =0旳基础解系为X X 12,,则AX b =旳通解为 .(三)解答题(第1小题9分,其他每题11分) 1.设有线性方程组λλλλλ11111112⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢⎤⎦⎥⎥⎥x y z λ为何值时,方程组有唯一解?或有无穷多解?2.判断向量β能否由向量组ααα123,,线性表出,若能,写出一种表出方式.其中βααα=---⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=-⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥=--⎡⎣⎢⎢⎢⎢⎤⎦⎥⎥⎥⎥83710271335025631123,,, 3.计算下列向量组旳秩,并且(1)判断该向量组与否线性有关;(2)求出该向量组旳一种极大无关组。
1.区间估计已知某种灯泡寿命服从正态分布,在某星期所生产的该灯泡中随机抽取10 只,测得其寿命(单位:小时)为1067 919 1196 785 1126 936 918 1156 920 948(1)试问这批灯泡中大约95%的灯泡至少使用多少小时;(2)求这批灯泡能够使用1000小时以上的概率。
解:(1)输入程序:X<-c(1067,919,1196,785,1126,936,918,1156,920,948)t.test(X,al="g")运行结果:One Sample t-testdata: Xt = 23.9693, df = 9, p-value = 9.148e-10alternative hypothesis: true mean is greater than 095 percent confidence interval:920.8443 Infsample estimates:mean of x997.1结果分析:有95%的灯泡至少可以使用920小时。
(2)输入程序:x<-c(1067,919,1196,785,1126,936,918,1156,920,948)pnorm(1000,mean(x),sd(x))运行结果:[1] 0.5087941结果分析:灯泡能够使用1000小时以上的概率为1-0.5087941=0.4912059,即49.12%2.假设检验I正常男子血小板计数均值为225 x 109/L,今测得20名男性油漆作业工人的血小板计数值(单位:109/L)220 188 162 230 145 160 238 188 247 113126 245 164 231 256 183 190 158 224 175问油漆工人的血小板计数与正常成年男子有无差异,并说明油漆作业对人体血小板计数是否有影响.解:设原假设为H0:225=μ对立假设H1:225≠μ输入程序:X<-c(220,188,162,230,145,160,238,188,247,113,126,245,164,231,256,183,190,158,224,175)t.test(X,mu=225)结果:One Sample t-testdata: Xt = -3.4783, df = 19, p-value = 0.002516alternative hypothesis: true mean is not equal to 22595 percent confidence interval:172.3827 211.9173sample estimates:mean of x192.15可以看出,P-=0.002516<0.05,所以拒绝H,置信区间为[172.3827,211.9173],最大值小于225。
因此可以认为油漆作业对人体血小板计数有影响。
3.假设检验II为研究某铁剂治疗和饮食治疗营养性缺铁性贫血的效果,将16名患者按年龄、体重、病程和病情相近的原则配成8对,分别使用饮食疗法和补充铁剂治疗的方法,三个月后测得两种患者血红蛋白如表5.1所示,问两种方法治疗后的表5.1铁剂和饮食两种方法治疗后患者血红蛋白值(g/L)患者血红蛋白有无差异.请选择两总体方差相同模型、两总体方差不同模型和成对数据模型作检验,并分析三种方法优缺点。
解:(1)两总体方差相同时:设原假设H0:21μ=μ对立假设H1:21μ≠μ输入程序:X<-c(113,120,138,120,100,118,138,123)Y<-c(138,116,125,136,110,132,130,110)t.test(X, Y, var.equal=TRUE)结果:Two Sample t-testdata: X and Yt = -0.566, df = 14, p-value = 0.5804alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval:-16.164884 9.414884sample estimates:mean of x mean of y121.250 124.625分析结果:P-值=0.58>0.05,接受原假设H,所以两种方法治疗后的患者血红蛋白有差异。
(2)两总体方差不同时原假设H0:21μ=μ对立假设H1:21μ≠μ输入程序:X<-c(113,120,138,120,100,118,138,123) Y<-c(138,116,125,136,110,132,130,110)t.test(X, Y)结果:Welch Two Sample t-testdata: X and Yt = -0.566, df = 13.855, p-value = 0.5805alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval:-16.177442 9.427442sample estimates:mean of x mean of y121.250 124.625可以看出,p值>0.05,接受原假设H,两种方法治疗后的患者血红蛋白有差异。
(3)成对数据模型调用函数"interval_estimate"输入程序:X<-c(113,120,138,120,100,118,138,123)Y<-c(138,116,125,136,110,132,130,110)interval_estimate(X-Y)结果:mean df a b1 -3.375 7 -15.62889 8.87889分析结果:0包含在置信区间内,所以两种方法治疗后的患者血红蛋白有差异。
4.假设检验III一项调查显示某城市老年人口比重为14.7%。
该市老年研究协会为了检验该项调查是否可靠,随机抽选了400名居民,发现其中有57人是老年人。
问调查结果是否支持该市老年人口比重为14.7%的看法(α= 0.05)。
解:设原假设H0:%7.14pp==对立假设H1:pp≠该模型符合二项分布故输入程序:binom.test(57,400,p=0.147)结果:Exact binomial testdata: 57 and 400number of successes = 57, number of trials = 400, p-value = 0.8876 alternative hypothesis: true probability of success is not equal to 0.147 95 percent confidence interval:0.1097477 0.1806511sample estimates:probability of success0.1425分析结果:P-值=0.9976>0.05,所以接受原假设H,认为该市老年人口比重为14.7%。
5.分布检验IMendel用豌豆的两对相对性状进行杂交实验,黄色圆滑种子与绿色皱缩种子的豌豆杂交后,第二代根据自由组合规律,理论分离比为黄圆:黄皱:绿圆:绿皱=9/16:3/16:3/16:1/16实际实验值为:黄圆315粒,黄皱101粒,绿圆108粒,绿皱32粒,共556粒,问此结果是否符合自由组合规律?解:设原假设H0:161,163,163,1694321====pppp输入程序:chisq.test(c(315,101,108,32),p=c(9,3,3,1)/16) 结果:Chi-squared test for given probabilitiesdata: c(315, 101, 108, 32)X-squared = 0.47, df = 3, p-value = 0.9254,认为此结果符合自由组合规可以看出,P-值=0.9254>0.05,所以接受原假设H律。
6.分布检验II观察每分钟进入某商店的人数X,任取200分钟,所得数据表5.2所示。
试分析,能否认为每分钟顾客数X服从Poisson分布(α= 0.1)。
表5.2每分钟进人商店顾客人数的频数解:设原假设H:服从Poisson分布输入程序:Z<-c(92, 68, 28, 12)n<-length(Z); p<-p[1:n-1]; p[n]<-1-q[n-1]chisq.test(Z, p=p)结果:Chi-squared test for given probabilitiesdata: ZX-squared = 0.9113, df = 3, p-value = 0.8227,认为每分钟顾客数X服从Poisson 分析结果:P-值=0.8227>0.05,接受原假设H分布。
7. 列联表检验I向120名女性和120名男性做调查,了解他们关于给谁买节日礼物最难的看法,调查结果如表5.3所示。
试分析:女性和男性在关于给谁买节日礼物最难的看法上没有显著差异。
表5.3关于给谁买节日礼物最难的看法性别给谁买节日礼物最难配偶父母子女兄弟姐妹姻亲其他亲属女性28 34 23 7 13 15 男性42 31 9 11 7 20 解:设:原假设男女买礼物无差异成立,对立假设男女存在差异输入R程序:x<-matrix(c(28, 42, 34, 31, 23, 9, 7, 11, 13, 7, 15, 20),nc=6)chisq.test(x)Pearson's Chi-squared testdata: XX-squared = 12.4666, df = 5, p-value = 0.02892运行结果分析:p-value = 0.02892<0.05,所以原假设不成立,实验结果表明男性女性在关于给谁买礼物最难问题上有差异。
8.列联表检验II为研究人脑的左右半球恶性肿瘤的发病率是否有显著差异,对人脑恶性肿瘤和良性肿瘤的发病情况做了调查,调查结果如表5.4所示。
试进行分析。
表5.4人脑左右半球恶性肿瘤和两性肿瘤的发病情况解:设:原假设H0左右脑半球发病率无差异,对立假设为存在差异输入R程序:x<-matrix(c(9,1,3,3),nc=2)fisher.test(x)结果:Fisher's Exact Test for Count Datadata: xp-value = 0.1181alternative hypothesis: true odds ratio is not equal to 195 percent confidence interval:0.4313171 521.0928115sample estimates:odds ratio7.63506运行结果分析:p-value = 0.1181>0.05,所以原假设成立,实验结果表明左右脑半球发病率无差异。