圆的基本性质和垂径定理

2019年中考数学备考资料：圆的基础性质公式定理2019年中考数学备考资料：圆的基础性质公式定理圆是轴对称图形，同时圆也是中心对称图形，其对称中心是圆心。

圆的基础性质⑴垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的2条弧。

逆定理：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的2条弧。

⑵有关圆周角和圆心角的性质和定理①在同圆或等圆中，如果两个圆心角，两个圆周角，两组弧，两条弦，两条弦心距中有一组量相等，那么他们所对应的其余各组量都分别相等。

②一条弧所对的圆周角等于它所对的圆心角的一半。

直径所对的圆周角是直角。

90度的圆周角所对的弦是直径。

圆心角计算公式:θ=(L/2πr)×360°=180°L/πr=L/r(弧度)即圆心角的度数等于它所对的弧的度数;圆周角的度数等于它所对的弧的度数的一半。

③如果一条弧的长是另一条弧的2倍，那么其所对的圆周角和圆心角是另一条弧的2倍。

⑶有关外接圆和内切圆的性质和定理①一个三角形有唯一确定的外接圆和内切圆。

外接圆圆心是三角形各边垂直平分线的交点，到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角平分线的交点，到三角形三边距离相等。

③R=2S△÷L(R：内切圆半径，S：三角形面积，L：三角形周长)④两相切圆的连心线过切点(连心线：两个圆心相连的直线)⑤圆O中的弦PQ的中点M，过点M任作两弦AB，CD，弦AD与BC分别交PQ于X，Y，则M为XY之中点。

(4)如果两圆相交，那么连接两圆圆心的线段(直线也可)垂直平分公共弦。

(5)弦切角的度数等于它所夹的弧的度数的一半。

(6)圆内角的度数等于这个角所对的弧的度数之和的一半。

(7)圆外角的度数等于这个角所截两段弧的度数之差的一半。

(8)周长相等，圆面积比长方形、正方形、三角形的面积大。

圆的知识要领不仅常考公式，又是也会直接出一些关于定理的试题。

《圆的基本性质》的知识点及典型例题知识框图1、过一点可作个圆。

过两点可作个圆，以这两点之间的线段的上任意一点为圆心即可。

过三点可作个圆。

过四点可作个圆。

2、垂径定理：垂直于弦的直径，并且平分垂径定理的逆定理1：平分弦（）的直径垂直于弦，并且平分垂径定理的逆定理2：平分弧的直径3、圆心角定理：在同圆或等圆中，相等的圆心角所对的，所对的圆心角定理的逆定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么都相等。

注解：在由“弦相等，得出弧相等”或由“弦心距相等，得出弧相等”时，这里的“弧相等”是指对应的劣弧与A B，那么所求的是弧长劣弧相等，优弧与优弧相等。

在题目中，若让你求⌒4.圆周角性质:①圆周角等于它所对的弧所对的圆心角的一半.②同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等.③90°的圆周角所对的弦为直径；半圆或直径所对的圆周角为直角.④如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.⑤圆内接四边形的对角互补；外角等于它的内对角.练习一、 填空题：1、 如图，在⊙O 中，弦AB ∥OC ，115AOC ∠=︒，则BOC ∠=_________2、如图，在⊙O 中，AB 是直径，15C ∠=︒，则BAD ∠=__________3、如图，点O 是ABC ∆的外心，已知40OAB ∠=︒，则ACB ∠=___________（1题图） （2题图） （3题图） （4题图） 4、如图，AB 是⊙O 的直径，弧BC=弧BD ，25A ∠=︒，则BOD ∠= ．（5题图） （6题图） （7题图） 5、如图，⊙O 的直径为8，弦CD 垂直平分半径OA ，则弦CD ＝ ．6、已知⊙O 的半径为2cm ，弦AB ＝2cm ，P 点为弦AB 上一动点，则线段OP 的范围是 ．7、如图，在⊙O 中，∠B=50º，∠C=20º，则∠BOC 的=____________8、在半径为5cm 的圆中，两条平行弦的长度分别为6cm 和8cm ，则这两条弦之间的距离为 9、在半径为1的⊙O 中，弦AB 、AC 分别是3和2，则∠BAC 的度数为__________________10、如图，某花园小区一圆形管道破裂，修理工准备更换一段新管道，现在量得污水水面宽度为80cm ，水面到管道顶部距离为20cm ，则修理工应准备内直径是_________cm 的管道．．半径为5cm 的圆O中有一点P ，OP=4，则过P 的最短弦长_________，最长弦是__________，二、 选择题：12．如图，矩形与⊙O 相交，若AB=4，BC=5，DE=3，则EF 的长为（ ）A ． 3.5B ． 6.5C ． 7D ． 813、如图，AB 是⊙O 的直径，AD=DE ，AE 与BD 交于点C ，则图中与∠BCE 相等的角有（ ）A.2个B.3个C.4个D.5个B OCAO ABCDOABCD BOACDBOACOABPABCON M OFEDC B A1、已知如图,AB 为⊙O 的弦,半径OE 、OF 分别交AB 于点C 、D ，且AC=BD 。

圆的基本性质与定理一有关圆的基本性质与定理⑴圆的确定：画一条线段,以线段长为半径以一端点为圆心画弧绕360度后得到圆.圆与直线相切圆的对称性质：圆是轴对称图形,其对称轴是任意一条通过圆心的直线.圆也是中心对称图形,其对称中心是圆心.垂径定理：垂直于弦的直径平分这条弦,并且平分弦所对的2条弧.逆定理：平分弦（不是直径）的直径垂直于弦,并且平分弦所对的2条弧. ⑵有关圆周角和圆心角的性质和定理在同圆或等圆中,如果两个圆心角,两个圆周角,两组弧,两条弦,两条弦心距中有一组量相等,那么他们所对应的其余各组量都分别相等.一条弧所对的圆周角等于它所对的圆心角的一半.直径所对的圆周角是直角.90度的圆周角所对的弦是直径. 如果一条弧的长是另一条弧的2倍,那么其所对的圆周角和圆心角是另一条弧的2倍. ⑶有关外接圆和内切圆的性质和定理①一个三角形有唯一确定的外接圆和内切圆.外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等；②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等.③R=2S△÷L（R：内切圆半径,S：三角形面积,L：三角形周长）④两相切圆的连心线过切点（连心线：两个圆心相连的直线）⑤圆O中的弦PQ的中点M,过点M任作两弦AB,CD,弦AD与BC分别交PQ于X,Y,则M为XY之中点. （4）如果两圆相交,那么连接两圆圆心的线段（直线也可）垂直平分公共弦. （5）圆心角的度数等于它所对的弧的度数. （6）圆周角的度数等于它所对的弧的度数的一半. （7）弦切角的度数等于它所夹的弧的度数的一半. （8）圆内角的度数等于这个角所对的弧的度数之和的一半. （9）圆外角的度数等于这个等于这个角所截两段弧的度数之差的一半.〖有关切线的性质和定理〗圆的切线垂直于过切点的半径；经过半径的一端,并且垂直于这条半径的直线,是这个圆的切线. 切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线. 切线的性质：（1）经过切点垂直于这条半径的直线是圆的切线.（2）经过切点垂直于切线的直线必经过圆心.（3）圆的切线垂直于经过切点的半径. 切线长定理：从圆外一点到圆的两条切线的长相等,那点与圆心的连线平分切线的夹角. 〖有关圆的计算公式〗 1.圆的周长C=2πr=πd 2.圆的面积S=πr^2; 3.扇形弧长l=nπr/180 4.扇形面积S=(nπr^2)/360=lr/2(l为扇形的弧长）5.圆锥侧面积S=πrl 6.圆锥侧面展开图（扇形）的圆心角n=360r/l(r是底面半径,l是母线长) [编辑本段]【圆的解析几何性质和定理】〖圆的解析几何方程〗圆的标准方程：在平面直角坐标系中,以点O（a,b）为圆心,以r为半径的圆的标准方程是(x-a)^2+(y-b)^2=r^2. 圆的一般方程：把圆的标准方程展开,移项,合并同类项后,可得圆的一般方程是x^2+y^2+Dx+Ey+F=0(其中D^2+E^2-4F＞0）.其中和标准方程对比,其实D=-2a,E=-2b,F=a^2+b^2-r^2.该圆圆心坐标为（-D/2,-E/2),半径r=0.5√D^2+E^2-4F. 圆的离心率e=0,在圆上任意一点的曲率半径都是r. 经过圆x^2+y^2=r^2上一点M（a0,b0）的切线方程为a0*x+b0*y=r^2 〖圆与直线的位置关系判断〗平面内,直线Ax+By+C=0与圆x^2+y^2+Dx+Ey+F=0的位置关系判断一般方法是： 1.由Ax+By+C=0,可得y=（-C-Ax）／B,（其中B不等于0）,代入x^2+y^2+Dx+Ey+F=0,即成为一个关于x的一元二次方程f（x）=0.利用判别式b^2-4ac的符号可确定圆与直线的位置关系如下：如果b^2-4ac>0,则圆与直线有2交点,即圆与直线相交。

圆 基本元素：圆的定义，圆心，半径，弧，弦，弦心距的 垂径定理认 对称性：旋转不变性，轴对称，中心对称（强）识 圆心角、弧、弦、弦心距的关系与圆有关的角：圆心角，圆周角（一）圆的性质1、旋转不变性：圆是旋转对称图形，绕圆心旋转任一角度都和原来图形重合；2、圆是中心对称图形，对称中心是圆心．性质：在同圆或等圆中，如果两个圆心角，两条弧，两条弦，两个弦心距中有一对量相等，那么它们所对应的其余各对量也分别相等。

3、轴对称：圆是轴对称图形，经过圆心的任一直线都是它的对称轴．（二）与圆有关的角⑴ 圆心角：顶点在圆心的角叫圆心角。

圆心角的性质：圆心角的度数等于它所对的弧的度数。

⑵ 圆周角：顶点在圆上，两边都和圆相交的角叫做圆周角。

圆周角的性质：① 圆周角等于它所对的弧所对的圆心角的一半．② 同弧或等弧所对的圆周角相等；在同圆或等圆中，相等的圆周角所对的弧相等．③ 90°的圆周角所对的弦为直径；半圆或直径所对的圆周角为直角．（三）垂径定理及应用垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的弧垂径定理是圆的重要内容，在实际生活中有着广泛的应用. 在各地中考题中对垂径定理的考查频频出现，这类问题常常结合勾股定理来解决。

1、求半径例1.高速公路的隧道和桥梁最多．图1是一个隧道的横截面，若它的形状是以O 为圆心的圆的一部分，路面A B =10米，净高C D =7米，则此圆的半径O A =（ ）（A ）5 （B ）7 （C ）375 （D ）3772、求弦长例2.工程上常用钢珠来测量零件上小孔的直径，假设钢珠的直径是10mm ，测得钢珠顶端离零件表面的距离为8mm ，如图2所示，则这个小孔的直径A B ＿＿＿＿mm ． 图1 OD AB C3、求弦心距 例3.如图4，O 的半径为5，弦8A B =，O C A B ⊥于C ，则O C 的长等于 ．4、求拱高例4.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图5所示，已知AB =16m ，半径 OA =10m ，高度CD为_____m ． 五、求角度例5.如图6，在⊙O 中，AB 为⊙O 的直径，弦CD ⊥AB ，∠AOC =60º，则∠B = ．六、探究线段的最小值例6.如图7，⊙O 的半径OA =10cm ，弦AB =16cm ，P 为AB 上一动点，则点P 到圆心O 的最短距离为 cm ． D C O A B图3 B A 8mm图2 图4COA B DC A OB 图5CODAB 图6综合巩固练习：1、如图1，O ⊙的直径A B 垂直弦C D 于P ，且P 是半径O B 的中点，6cm C D ，则直径A B 的长是（ ）A ．23cmB ．32cmC ．42cmD ．43cm2、如图2，⊙O 的弦AB =6，M 是AB 上任意一点，且OM 最小值为4，则⊙O 的半径为（ ）A ．5B ．4C ．3D ．23、如图3，⊙O 是△ABC 的外接圆，已知∠B =60°，则∠CAO 的度数是( )A ．15°B ．30°C ．45°D ．60°4、一根水平放置的圆柱形输水管道横截面如图所示，其中有水部分水面宽0.8米，最深处水深0.2米，则此输水管道的直径是（ ）．A ．0.4米B ．0.5米C ．0.8米D ．1米图1 图2 图3 图49、如图（十），分别是的直径和弦，于点，连结、，，，则 ．C OA B P图711、如图，圆弧形桥拱的跨度AB ＝12米，拱高CD ＝4米，则拱桥的半径为（ ）A ．6.5米B ．9米C ．13米D ．15米13、本市新建的滴水湖是圆形人工湖。

干货：圆的相关定理，性质，公式盘点不要害怕拒绝他人，如果自己的理由出于正当。

当一个人开口提出要求的时候，他的心里根本预备好了两种答案。

所以，给他任何一个其中的答案，都是意料中的。

——三毛1、垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.∵CD是圆O的直径,CD⊥AB∴AP=BP,弧AC=弧BC,弧AD=弧BD2、弧，弦，圆心角(1)在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.(2)在圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.(3)在一个圆中,如果弦相等,那么它所对的弧相等,所对的圆心角相等.∵ ∠COD =∠AOB∴AB=CD,弧AB=弧CD3、圆周角定理及推论在同圆或等圆中,同弧所对的圆周角等于它所对的圆心角的一半。

∠A =1/2∠O在同圆或等圆中,同弧或等弧所对的所有的圆周角相等。

相等的圆周角所对的弧相等。

∠C=∠D=∠E=1/2∠AOB半圆或直径所对的圆周角都相等,都等于90°(直角)。

90°的圆周角所对的弦是圆的直径。

∵AB是⊙O的直径∴∠C=∠D=∠E=90°（∵∠C=90°，∴AB是⊙O的直径）4、点与圆，直线与圆的位置关系一、(1)点在圆外，d＞r;(2)点在圆上，d =r;(3)点在圆内，d＜r.二、 (1)当直线与圆相离时d＞r;(2)当直线与圆相切时d =r;(3)当直线与圆相交时d＜r.三、切线的判定与性质判定：经过半径的外端且垂直于这条半径的直线是圆的切线。

∵OA是⊙O的半径,OA⊥ l∴直线l是⊙O的切线.性质：圆的切线垂直于经过切点的半径.∵直线l是⊙O的切线,切点为A∴ OA⊥ l切线长定理：从圆外一点引圆的两条切线，它们的切线长相等；这点与圆心的连线平分这两条切线的夹角。

∵PA、PB为⊙O的切线∴PA=PB,∠APO= ∠BPO5、三角形的外心是三角形各边垂直平分线的交点.三角形的内心是三角形各角平分线的交点.6、弧长，扇形面积，圆锥侧面积计算公式S侧面积=πra。

[圆的基本性质与定理]1定理: 不在同一直线上的三点确定一个圆。

(圆的确定）2圆的对称性质：圆是轴对称图形，其对称轴是任意一条过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

3垂径定理:垂直于弦的直径平分这条弦并且平分弦所对的两条弧推论1 ①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧推论2 圆的两条平行弦所夹的弧相等、圆是以圆心为对称中心的中心对称图形[有关圆周角和圆心角的性质和定理]1定理: 在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半圆心角定理圆心角的度数等于他所对的弧的度数推论1 同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等推论2半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形圆内接四边形的性质与定理]1定理圆的内接四边形的对角互补2定理并且任何一个外角都等于它的内对角3圆内接四边形判定定理如果一个四边形对角互补，那么这个四边形的四个顶点共圆推论如果一个四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆[有关切线的性质和定理]1切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线2切线的性质定理：圆的切线垂直于经过切点的半径推论1：经过圆心且垂直于切线的直线必经过切点推论2 ：经过切点且垂直于切线的直线必经过圆心[圆的其他性质定理]1弦切角定理弦切角等于它所夹的弧对的圆周角推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等2①直线L和⊙O相交d＜r ②直线L和⊙O相切d=r ③直线L和⊙O相离d＞r3圆的外切四边形的两组对边的和相等[圆与圆]1如果两个圆相切，那么切点一定在连心线上2①两圆外离d＞R+r ②两圆外切d=R+r ③两圆相交R-r＜d＜R+r(R＞r) ④两圆内切d=R-r(R＞r) ⑤两圆内含d＜R-r(R＞r)3定理相交两圆的连心线垂直平分两圆的公共弦4定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形（有关外接圆和内切圆的性质和定理）5定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆6一个三角形有唯一确定的外接圆和内切圆。

初三数学圆的性质定理1、圆的对称性：圆是轴对称图形，任一条直径所在的直线都是它的对称轴.2、垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧.3、垂径定理的推论：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧.4、垂径定理的应用：①用直尺和圆规平分一条弧.作法是过圆心作弧所对弦的垂线，理由是垂径定理；②在利用垂径定理计算或证明时，我们通常将其化为一个直角三角形的边和角，这个特殊直角三角形的三边分别是半径、弦的一半和圆心到弦的垂线段.例1、如图，已知以点O为公共圆心的两个同心圆，大圆的弦AD交小圆于B、C.(1)求证：AB=CD(2)如果AD=6cm，BC=4cm，求圆环的面积.1.圆周角定义：顶点在圆周上，并且两边都和圆相交的角叫做圆周角.2.圆周角定理：同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半.3.推论：①同圆或等圆中，相等的圆周角所对的弧一定相等.②半圆（或直径）所对圆周角是直角，90°的圆周角所对的弦是直径.③如果三角形一边上的中线等于这条边的一半，那么这个三角形是直角三角形.4．圆的内接四边形：①定义：如果一个多边形的所有顶点都在同一圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.②圆内接四边形的性质：圆内接四边形的对角互补.例2、如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交BC于D.若BC=8，ED=2，求⊙O的半径.1、如图，已知AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP∶PB=1∶5，那么⊙O的半径是（）2、圆的半径为13cm，两弦AB∥CD，AB=24cm，CD=10cm，则两弦AB、CD的距离是（）A．7cm B．17cm C．12cm D．7cm或17cm3、如下图所示，AB是⊙O的一条固定直径，它把⊙O分成上、下两个半圆，自上半圆上一点C作弦CD⊥AB，∠OCD的平分线交⊙O于点P，当点C在上半圆（不包括A、B两点）移动时，点P（）A．到CD的距离保持不变B．位置不变C．平分D．随点C的移动而移动4、如上中图，BD是⊙O的直径，弦AC、BD相交于点E，则下列结论不成立的是（）A．∠ABD=∠ACD B．C．∠BAE=∠BDC D．∠ABD=∠BDC5、如上右图，⊙O的直径CD过弦EF的中点G，∠EOD=40°，则∠DCF等于（）A．80°B．50°C．40°D．20°6、如下图，A、B、C是⊙O上三点，∠ACB=40°，则∠ABO等于__________度．7、如上左二图，△ABC的顶点都在⊙O上，∠C=30°，AB=2cm，则⊙O的半径为__________cm．8、如上左三图，在平面直角坐标系中，P是经过O（0，0），A（0，2），B（2，0）的圆上的一个动点（P与O、A 、B不重合），则∠OAB=__________，∠OPB=__________．9、如右上图，△ABC内接于⊙O，∠B=∠OAC，OA=8cm，则AC=__________cm．10、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC，BD为⊙O的直径，AD=6，则BC=__________．11、如图，⊙O中的弦AB、CD互相垂直于E，AE=5cm，BE=13cm，O到AB的距离为．求⊙O的半径及O到CD的距离．12、如图，某地有一座圆弧形的拱桥，桥下水面宽为7.2m，拱顶高出水面2.4m，现有一艘宽3m，船舱顶部为正方形并高出水面2m的货船要经过这里，此时货船能顺利通过这座拱桥吗？请说明理由．13、如图，AB为⊙O的直径，BD是⊙O的弦，延长到C，使BD＝DC，连接AC交⊙O于点F，点F不与点A重合．（1）AB与AC的大小有什么关系？为什么？（2）按角的大小分类，请你判断△ABC属于哪一类三角形，并说明理由．一、确定圆的条件(1)因为作圆实质上是确定圆心和半径，要经过已知点A作圆，只要圆心确定下来，半径就随之确定了下来．所以以点A以外的任意一点为圆心，以这一点与点A所连的线段为半径就可以作一个圆．由于圆心是任意的．因此这样的圆有无数个．如图(1)．(2)已知点A、B都在圆上，它们到圆心的距离都等于半径．因此圆心到A、B的距离相等．根据前面提到过的线段的垂直平分线的性质可知，线段的垂直平分线上的点到线段两端点的距离相等，则圆心应在线段AB的垂直平分线上．在AB的垂直平分线上任意取一点，都能满足到A、B两点的距离相等，所以在AB的垂直平分线上任取一点都可以作为圆心，这点到A的距离即为半径，圆就确定下来了．由于线段AB的垂直平分线上有无数点，因此有无数个圆心，作出的圆有无数个．如图(2)．(3)要作一个圆经过A、B、C三点，就是要确定一个点作为圆心，使它到三点的距离相等．因为到A、B两点距离相等的点的集合是线段AB的垂直平分线，到B、C两点距离相等的点的集合是线段BC的垂直平分线，这两条垂直平分线的交点满足到A、B、C三点的距离相等，就是所作圆的圆心．因为两条直线的交点只有一个，所以只有一个圆心，即只能作出一个满足条件的圆．过不在同一条直线上的三点确定一个圆2、经过三角形三个顶点的圆，叫做三角形的外接圆，外接圆的圆心是三角形三边垂直平分线的交点，叫做三角形的外心，这个三角形叫做这个圆的内接三角形．因为画圆的关键是确定圆心和半径，所以作三角形的外接圆时，只要找三边垂直平分线的交点，这就是圆心，以这点到三角形任一顶点间的距离为半径就可作出三角形的外接圆．3、利用尺规过不在同一条直线上的三个点作圆的方法作法图示1．连结AB、BC2．分别作AB、BC的垂直平分线DE和FG，DE和FG相交于点O3．以O为圆心，OA为半径作圆⊙O就是所要求作的圆例1、已知锐角三角形、直角三角形、钝角三角形，分别作出它们的外接圆，它们外心的位置有怎样的特点？（1）（2）（3）例3、如图，点A、B、C表示三个村庄，现要建一座深水井泵站，向三个村庄分别送水，为使三条输水管线长度相同，水泵站应建在何处？请画出图，并说明理由．1、下列关于外心的说法正确的是（）A．外心是三个角的平分线的交点 B．外心是三条高的交点C．外心是三条中线的交点 D．外心是三边的垂直平分线的交点2、下列条件中不能确定一个圆的是（）A．圆心和半径B．直径 C．三角形的三个顶点D．平面上的三个已知点3、三角形的外心具有的性质是（）A．到三边的距离相等B．到三个顶点的距离相等 C．外心在三角形外D．外心在三角形内4、等腰三角形底边上的中线所在的直线与一腰的垂直平分线的交点是（）A．重心B．垂心 C．外心D．无法确定5、如图所示，在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（）A．点P B．点Q C．点R D．点M6、如图，是△ABC的外接圆，∠BAC=30°，BC=2 cm ，则△OBC的面积是_______.7、直角三角形的两边长分别为16和12，则此三角形的外接圆半径是_______．8、如图，有一个圆形的盖水桶的铁片，部分边沿由于水生锈残缺了一些，很不美观，为了废物利用，将铁片剪去一些使其成为圆形的，应找到圆心，并找到合理的半径，在铁片上画出圆，沿圆剪下即可，问应怎么样找到圆心和半径？。

[圆的基本性质与定理]1定理:不在同一直线上的三点确定一个圆。

(圆的确定）2圆的对称性质：圆是轴对称图形，其对称轴是任意一条过圆心的直线。

圆也是中心对称图形，其对称中心是圆心。

3垂径定理:垂直于弦的直径平分这条弦并且平分弦所对的两条弧推论1①平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧②弦的垂直平分线经过圆心，并且平分弦所对的两条弧③平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧推论2圆的两条平行弦所夹的弧相等、圆是以圆心为对称中心的中心对称图形[有关圆周角和圆心角的性质和定理]1定理:在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等推论在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等2圆周角定理一条弧所对的圆周角等于它所对的圆心角的一半圆心角定理圆心角的度数等于他所对的弧的度数推论1同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等推论2半圆（或直径）所对的圆周角是直角；90°的圆周角所对的弦是直径推论3如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形圆内接四边形的性质与定理]1定理圆的内接四边形的对角互补2定理并且任何一个外角都等于它的内对角3圆内接四边形判定定理如果一个四边形对角互补，那么这个四边形的四个顶点共圆推论如果一个四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆[有关切线的性质和定理]1切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线2切线的性质定理：圆的切线垂直于经过切点的半径推论1：经过圆心且垂直于切线的直线必经过切点推论2：经过切点且垂直于切线的直线必经过圆心[圆的其他性质定理]1弦切角定理弦切角等于它所夹的弧对的圆周角推论：如果两个弦切角所夹的弧相等，那么这两个弦切角也相等2①直线L 和⊙O相交d＜r②直线L和⊙O相切d=r③直线L和⊙O相离d＞r3圆的外切四边形的两组对边的和相等[圆与圆]1如果两个圆相切，那么切点一定在连心线上2①两圆外离d＞R+r②两圆外切d=R+r③两圆相交R-r＜d＜R+r(R＞r)④两圆内切d=R-r(R＞r)⑤两圆内含d ＜R-r(R＞r)3定理相交两圆的连心线垂直平分两圆的公共弦4定理把圆分成n(n≥3):⑴依次连结各分点所得的多边形是这个圆的内接正n边形⑵经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形（有关外接圆和内切圆的性质和定理）5定理：任何正多边形都有一个外接圆和一个内切圆，这两个圆是同心圆6一个三角形有唯一确定的外接圆和内切圆。

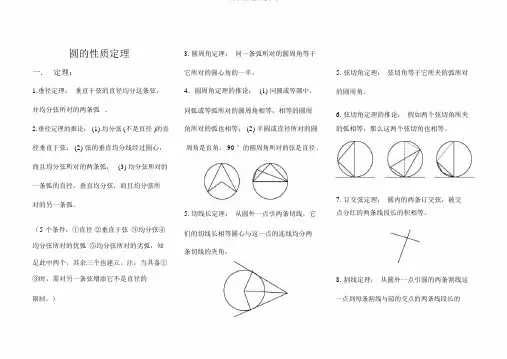
圆的性质定理一．定理：1.垂径定理：垂直于弦的直径均分这条弦，并均分弦所对的两条弧。

2.垂径定理的推论： (1) 均分弦 (不是直径 )的直径垂直于弦； (2) 弦的垂直均分线经过圆心，而且均分弦所对的两条弧；(3) 均分弦所对的一条弧的直径，垂直均分弦，而且均分弦所对的另一条弧。

（5 个条件：①直径②垂直于弦③均分弦④均分弦所对的优弧⑤均分弦所对的劣弧，知足此中两个，其余三个也建立。

注：当具备① ③时，需对另一条弦增添它不是直径的3.圆周角定理：同一条弧所对的圆周角等于它所对的圆心角的一半。

4．圆周角定理的推论：(1) 同圆或等圆中，同弧或等弧所对的圆周角相等，相等的圆周角所对的弧也相等； (2) 半圆或直径所对的圆周角是直角， 90 °的圆周角所对的弦是直径 .5.切线长定理：从圆外一点引两条切线，它们的切线长相等圆心与这一点的连线均分两条切线的夹角。

5.弦切角定理：弦切角等于它所夹的弧所对的圆周角。

6.弦切角定理的推论：假如两个弦切角所夹的弧相等，那么这两个弦切角也相等。

7.订交弦定理：圆内的两条订交弦，被交点分红的两条线段长的积相等。

8.割线定理：从圆外一点引圆的两条割线这限制。

）一点到每条割线与园的交点的两条线段长的积相等。

8.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比率中项。

二．性质：1.在同圆或等圆中，假如两个圆心角、两条弧，两条弦，两个弦心距中有一组量相等，那么他们所对应的其余各组量分别相等。

2.确立圆的条件：定理：不在同一条直线上的三个点确立（有且只有）一个圆。

（作法：连结随意两点并作此中垂线，以这两条中垂线的交点为圆心，以这一点到已知三点中随意一点的距离为半径作圆）3.切线性质概括：（ 1）垂直于切线（ 2 ）过切点（ 3）过圆心，假如一条直线知足这三个条件中随意 2 个，那么就知足第 3 个。

（碰到切点连半径）增补 3：切线五大性质：（1 ）切线与圆只有一个公共点（2）圆心到切线的距离等于半径（ 3）切线垂直于过切点的半径（4 ）经过圆心垂直于切线的直线必经过切点（5）经过切点垂直于切线的直线必经过圆心。

九年级圆的垂径定理知识点在九年级的数学学习中，圆的垂径定理是一个非常重要的概念，也是学习圆形的几何性质的关键之一。

在这篇文章中，我们将深入探讨圆的垂径定理的知识点，了解其背后的原理和应用。

一、圆的定义和性质首先，我们需要回顾一下圆的定义和基本性质。

在数学中，圆是由平面上所有到一个固定点的距离相等的点的集合组成。

而这个固定点被称为圆心，半径则是圆心到圆上任意一点的距离。

圆具有很多重要性质，例如任意两点到圆心的距离相等，直径是圆的特殊弦，且它的长度是半径的两倍，而弧则是圆上的一段曲线，它与圆心对应的角叫做圆心角。

二、垂径定理的表述圆的垂径定理是指，如果一个直径和一个弦垂直相交，那么它就是弦的垂径，且它把弦分为两个相等的部分。

或者反过来说，如果一个弦被圆心角所分为两个相等的部分，那么它就与直径垂直相交。

这个定理的表述可能有点晦涩难懂，但是我们可以通过几何图形来直观地理解。

三、垂径定理的证明圆的垂径定理是可以通过简单的几何推导证明的。

假设有一个圆，圆心为O，直径为AB，弦为CD垂直于直径AB于点E。

我们需要证明CE = DE。

首先，连接AC和BD，并假设它们交于点F。

由于CD垂直于AB，所以CDE是一个直角三角形。

而由于圆心角的性质，角COD的度数是弦CD对应的角，即∠COE。

由于COE和COD是同位角，所以它们的度数相等，即∠COE = ∠COD。

而∠COD是一个直角，所以∠COE也是一个直角。

因此，我们可以得出结论，CE与DE相等，即CE = DE，证明了定理。

四、垂径定理的应用垂径定理在实际学习和应用中非常有用。

例如，在解决证明问题时，我们可以利用垂径定理来简化问题和推导证明过程。

此外，垂径定理还与圆的切线有着密切的关系。

当一个直径与一个切线相交时，由于切线与半径垂直，我们可以通过垂径定理得出切线与直径相交的两点的性质。

最后，垂径定理也与三角形的性质相关。

当我们在一个三角形内有一个圆时，利用垂径定理可以推导得出一些重要的三角形性质，如内切圆和外接圆的性质等。

圆的基本性质1、过一点可作个圆。

过两点可作个圆，以这两点之间的线段的上任意一点为圆心即可。

过三点可作个圆。

过四点可作个圆。

2、垂径定理：垂直于弦的直径，并且平分垂径定理的逆定理1：平分弦（）的直径垂直于弦，并且平分 垂径定理的逆定理2：平分弧的直径3、圆心角定理：在同圆或等圆中，相等的圆心角所对的，所对的圆心角定理的逆定理：在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等，那么都相等。

4、圆周角定理：一条弧所对的圆周角等于它所对的圆周角定理推论1：半圆（或直径）所对的圆周角是；90°的圆周角所对的弦是圆周角定理推论2：在同圆或等圆中，所对的圆周角相等；相等的圆周角所对的也相等 例1、如图，已知AB 是O 的直径，弦CD ⊥AB 于点E ，点M 在O 上，∠M =∠D . (1)判断BC 、MD 的位置关系，并说明理由； (2)若AE =16，BE =4，求线段CD 的长； (3)若MD 恰好经过圆心O ，求∠D 的度数。

变式训练1、如图,O 是△ABC 的外接圆,OD ⊥AB 于点D ,交O 于点E ,∠C =60∘,如果O 的半径为2,则结论错误的是(D)A. AD =DBB. 错误！未定义书签。

AE ˆ=EB ˆC. OD =1D. AB =32、如图,O 的直径BD =4,∠A =60∘,则BC 的长度为( C) A. 3B. 2C. 32 D. 34 巩固训练1、如图所示,O 的半径为13,弦AB 的长度是24,ON ⊥AB ,垂足为N ,则ON =(A) A. 5B. 7C. 9D. 112、如图,在O 中,AB ˆ=AC ˆ,∠AOB =40∘,则∠ADC 的度数是(C)第1题图第2题图第3题图第4题图 A. 40∘B. 30∘C. 20∘D. 15∘3、如图,点A. B. C 是圆O 上的三点,且四边形ABCO 是平行四边形,OF ⊥OC 交圆O 于点F ,则∠BAF 等于(B)A. 12.5∘B. 15∘C. 20∘D. 22.5∘4、如图,AB 是O 的直径,C ,D 是O 上的两点,若∠BCD =28∘,则∠ABD =__62_∘.5、如图,A ,P ,B ,C 是圆上的四个点,∠APC =∠CPB =60∘，AP ，CB 的延长线相交于点D. (1)求证：△ABC 是等边三角形； (2)若∠PAC =90∘,AB =32，求PD 的长。

圆的性质与垂径定理一．知识整理1、圆的有关概念①圆是到定点的距离等于定长的点的集合，经过圆心的弦叫做直径，直径是圆中最大的弦。

②圆既是轴对称图形又是中心对称图形③圆心相等、半径不同的两个圆是同心圆，半径相同、圆心不同的两个圆是等圆。

2、圆心确定圆的位置，半径确定圆的大小，不在同一直线上的三点确定一个圆。

3、垂径定理以及它的推论垂径定理：垂直于弦的直径平行这条弦，并且平分弦所对的弧。

4、在同圆或等圆中，如果圆心角、弧、弦、弦心距四组两种有一组量相等，那么它所对应的其余的量也相等。

5、垂径定理及其推论1涉及了一条直线的4条性质：2⇒2①经过圆心（直径），②垂直于弦，③平分弦，④平分弦所对的弧(优/弧)，当一条直线具有其中的两条性质时，就能推出另外三条注意：（①、③作为条件时，被平分的弦不能是直径）；推论2为：圆的两条平行弦所夹的弧相等.6、把相关定理综合得：1⇒3在同圆或等圆中，如果两个圆心角、两条弧、两条弦或两条弦的弦心距中，有一组量相等，那么它们所对应的其余各组量分别相等；一、探索研究例1、判断下列命题的真假⑴平分弦的直径一定垂直于这条弦（）⑵在同一平面内，三点确定一个圆（）⑶如果弧相等，那么它所对应的圆心角也相等（）⑷同圆中两条等弧所对的弦一定相等（）⑸半径的2倍是直径（）A例2、已知如图，在⊙O中，直线AB⊥CD于E，AE=8cm，EB=2cm，求CD的长例3、⊙O的半径为13 cm，弦AB∥CD，AB=24cm，CD=10cm，求AB和CD的距离。

例4、已知如图在⊙O中，AB=AC,OD⊥AB于D,OE⊥AC于E，求证∠ODE=∠OED二、教学精讲1. 如图所示，圆O的直径AB和弦CD交于E，已知AE=6cm，EB=2cm，∠CEA=30°，求CD。

2. 圆O中若直径为25cm，弦AB的弦心距10cm，求弦长。

3.若圆的半径2cm，圆中一条弦长1cm，则此弦中点到此弦所对劣弧中点之间的距离？A B4. 圆内一条弦与直径的交角为30°，且分直径为1cm 和5cm 两段，求弦心距 ，弦长 ．5. 半径为5cm 的圆O 中有一点P ，OP=4，则过P 的最短弦长_________，最长弦是__________．6. 如图，AB 为⊙O 的直径，点C 在⊙O 上，∠BAC 的平分线交BC 于D ，交⊙O 于E ，且AC ＝6，AB ＝8，求CE 的长。

各个顶点可以确定一个圆，这个圆叫做，这个圆的圆心叫做，而这个三角形叫做这个。

4、直角三角形的外心是。

5、圆是轴对称图形，它的对称轴是。

6、垂径定理：如果圆的一条直径一条弦，那么这条直径这条弦，并且。

7、已知扇形的面积为2π，半径等于6，则它的圆心角等于20 度。

答案：1、圆心、半径、位置、大小；2、无数、垂直平分线；3、不在同一直线上、三角形的外接圆、三角形的外心、圆的内接三角形；4、直角三角形斜边上的中点；5、直径所在的直线（或经过圆心的直线）；6、垂直于、平分、平分这条弦所对的弧；二、选择题1．有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有( B )A．4个 B．3个 C． 2个 D． 1个2.如图，△ ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，则下列五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C ，⑤,正确结论的个数是（ B ）A、2个B、3个C、4个D、5个∠等于（ D ）3．如图，点B、C在⊙O上，且BO=BC，则BACA．60︒ B．50︒ C．40︒ D．30︒4．如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠B大小为 ( D )A．25° B．35° C．45° D．65°（第2题图）（第3题图）（第4题图）精解名题例1：基本概念1．下面四个命题中正确的一个是（D ）A ．平分一条直径的弦必垂直于这条直径B ．平分一条弧的直线垂直于这条弧所对的弦C ．弦的垂线必过这条弦所在圆的圆心D ．在一个圆内平分一条弧和它所对弦的直线必过这个圆的圆心2. 下列命题中，正确的是（ C ）．A ．过弦的中点的直线平分弦所对的弧B ．过弦的中点的直线必过圆心C ．弦所对的两条弧的中点连线垂直平分弦，且过圆心D ．弦的垂线平分弦所对的弧 策略点击：1、A 平分直径的弦有可能是直径，所以错；B 、不一定；C 、不一定过弦中点； 2、A ．B 不一定垂直弦；D 、不一定过弦中点 3.下列命题中，不正确的是（ A ）A.平分弦的直径垂直于弦B.垂直平分弦的直线必经过圆心C.垂直于弦的直径平分弦所对的弧D.平分弧的直径垂直平分弧所对的弦 4.下列语句中，正确的有( A )⑴相等的圆心角所对的弧相等；⑵平分弦的直径垂直于弦；⑶长度相等的两条弧是等弧； ⑷经过圆心的每一条直线都是圆的对称轴； (A)1个；(B)2个；(C)3个；(D)4个；例2、在ABC ∆中,︒=∠90ACB ,AB CD ⊥,D 是垂足，︒=∠30A ,cm AC 3=，以C 为圆心、cm 3为半径作圆C 。

中考信息速递之一——圆的性质与垂径定理【知识要点】一．圆的基本性质：1、圆的对称性：圆既是轴对称图形又是中心对称图形。

经过圆心的每一条直线都是它的对称轴。

圆心是它的对称中心。

圆绕圆心旋转任何角度，都能够与原图形重合，因此圆还具有旋转不变性。

2、确定圆的要素是：圆心、半径。

①圆心确定圆的位置，半径确定圆的大小，确定一个圆，两者缺一不可。

②不在同一条直线上的三点确定一个圆；③已知圆的直径的位置和长度可确定一个圆。

以点O为圆心的圆记“⊙O”，读作：“圆O”。

3、三角形的外接圆：锐角三角形的外心在，钝角三角表的外心在，直角三角形的外心在。

4、圆的相关概念：（1）弦（2）弦心距（3）弧（4）半圆（5）优弧（6）劣弧（7）等弧（8）弓形（9）弓高（10）同心圆（11）等圆5．点与圆的位置关系：设⊙Ｏ的半径为r，则点P与⊙O的位置关系有：（１）点Ｐ在⊙Ｏ上ＯＰ＝r（２）点Ｐ在⊙Ｏ内ＯＰ＜r（３）点Ｐ在⊙Ｏ外ＯＰ＞r6．证明几个点在同一个圆上的方法：要证明几个点在同一个圆上，只要证明这几个点与一个定点的距离相等。

二.垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两弧．推论1：①平分弦（不是直径）的直径重直于弦，并且平分弦所对的两条弧．②弦的垂直平分线经过圆心，并且平分弦所对的两条弧．③平分弦所对的一条弧的直径,垂直平分弦，并且平分弦所对的另一条弧．推论2: 圆的两条平行弦所夹的弧相等．垂径定理及推论1中的三条可概括为四点：（1）经过圆心（2）垂直于弦（3）平分弦（4）平分弧．以上四点已知其中的任意两点，都可以推得其它两点．垂径定理及推论是解决有关弦的问题的重要理论根据，也是今后进一步学习新知识的基础，中考时可在填空或选择中单独命题，更多的是与其它部分的知识综合考查．C【典型例题】例1．试根据圆的定义填空：1、圆上各点到 的距离都等于 。

2、到定点的距离等于定长的点都在 。

例2．（1）已知⊙O 的半径r=2cm, 当OP 时，点P 在⊙O 上； 当OA=1cm 时，点A 在 ； 当OB=4cm 时，点B 在 。