国科大_小波与滤波器设计2010春季

设数字滤波器信号dwt的三级分解算法树型结构小波变换的时频分析小波与滤波器组信号dwt的三级分解算法等效的简化结构小波变换与滤波器组小波变换的时频分析小波与滤波器组的频率特性分解算法中滤波器组的频域分析小波与滤波器组信号dwt的分布小波与滤波器组信号时域表达的时频分辨率信号频域表达的时频分辨率小波变换与滤波器组小波与滤波器组信号stft的时频分辨率信号dwt的时频分辨率小波变换的时频分析小波与滤波器组小波基函数具有非唯一性这使得小波分的信号采用不同的小波基信号从而使得变换后的小波系数更稀散更加易于信号分析和处理
∑
k
c j [k] ⋅ 2 ϕ(2 j t − k) +
小波与滤波器组
∑
k
d j [k] ⋅ 2 j / 2ψ (2 j t − k)
小波变换与滤波器组
离散小波变换的分解算法
c j [ k ] = x (t ), ϕ j ,k (t ) = ∫ x (t ) ⋅ 2 j / 2 ϕ ( 2 j t − k )dt
小波与滤波器组
小波变换与滤波器组
小波变换的时频分析
H0(z) H0(z) H0 (z) c+1[k] J H1(z) ↓2 ↓2 H1 (z) ↓2 ↓2 H1(z) ↓2 d −2[k] [k J d −1[k] J d [k] J ↓2 c −2[k] J
信号DWT的三级分解算法树型结构 的三级分解算法树型结构 信号
d j [ k ] = x (t ),ψ j , k (t ) = ∫ x (t ) ⋅ 2 j / 2ψ ( 2 j t − k )dt
c j [ k ] = ∑ h[i − 2k ] ⋅ ∫ x(t ) ⋅ 2 ( j +1) / 2 ϕ ( 2 j +1 t − i )dt

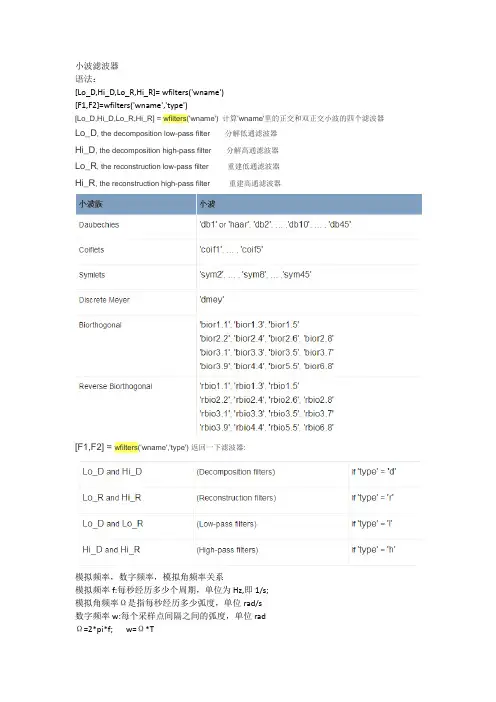
小波滤波器语法：[Lo_D,Hi_D,Lo_R,Hi_R]= wfilters('wname')[F1,F2]=wfilters('wname','type')[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('wname') 计算'wname'里的正交和双正交小波的四个滤波器Lo_D, the decomposition low-pass filter 分解低通滤波器Hi_D, the decomposition high-pass filter 分解高通滤波器Lo_R, the reconstruction low-pass filter 重建低通滤波器Hi_R, the reconstruction high-pass filter 重建高通滤波器[F1,F2] = wfilters('wname','type') 返回一下滤波器:模拟频率，数字频率，模拟角频率关系模拟频率f:每秒经历多少个周期，单位为Hz,即1/s;模拟角频率Ω是指每秒经历多少弧度，单位rad/s数字频率w:每个采样点间隔之间的弧度，单位radΩ=2*pi*f; w=Ω*TIIR数字滤波器设计方法：先根据已知带通参数求出最佳滤波器阶数和截止频率[n,Wn]=buttord(Wp,Ws,Rp,Rs);[n,Wn]=buttord(Wp,Ws,Rp,Rs,'s');[b,a]=butter(n,Wn,'ftype','s')Wp为0-1之间，Ws为阻带角频率，0-1之间。

Rp为通带波纹，或者通带衰减，Rs为阻带衰减。

给出的是模拟频率fp1通带截止频率，fp2阻带截止频率，则Wp=fp1*2/fs,Ws=fp2*2/fs。

传统FIR滤波器函数FIRl是采用经典窗函数设计线性相位FIR数字滤波器，且具有标准低通、带通、高通和带阻等类型。

电 子 科 技 大 学实 验 报 告学生姓名： 学 号： 指导教师：一、实验室名称：数字信号处理实验室二、实验项目名称：数字滤波器的设计及实现三、实验原理：一．数字滤波器设计：1．数字滤波器设计步骤：（1） 根据给定的滤波器设计要求，得到参数化描述，即通带，阻带截止频率p ω和s ω，通带阻带纹波p δ和s δ等数据。

（2） 找一个数字系统函数G(z)，使其频率响应逼近设计要求。

（3） 择合适的滤波器结构对满足要求的传递函数G(z)进行实现。

2．数字滤波器设计中的注意事项：（1） 设计要求的参数化：图1给出了一个典型的数字低通滤波器的幅频特性说明。

理解每个参数的物理含义。

（2）IIR 滤波器和FIR FIR 的两倍；另外，FIR IIR 滤波器除较FIR 滤波器有很大的优势。

根据以上这些区别，结合实际的设计要求，就可以选择一款合适的滤波器。

（3） 波器设计的方法：由于IIR 滤波器和FIR 滤波器各自的结构特点，所以它们的设计方法也不一样。

在IIR 滤波器的设计中，常用的方法是：先根据设计要求寻找一个合适的模拟原型滤波器)(s H a ，然后根据一定的准则将此模拟原型滤波器转换为数字滤波器)(z G ，即为我们需要设计的数字滤波器。

在FIR 滤波器设计中，一般使用比较直接的方法：根据设计的要求在时域对理想的冲击S ω - P ω - P ωS ω 通带 阻带 过渡带 图1.典型的数字LPF 幅频特性响应序列进行加窗逼近，或从频域对需要实现的频率响应特性进行采样逼近然后进行反FFT 。

（4） 波器阶数估计：IIR 滤波器的阶数就等于所选的模拟原型滤波器的阶数，所以其阶数确定主要是在模拟原型滤波器设计中进行的。

FIR 滤波器阶数估计可以根据很多工程中的经验公式，这些公式可以直接从设计的参数要求中估计滤波器阶数。

例如，对FIR 低通滤波器，已知通带截止频率p ω，阻带截止频率s ω，最大通带纹波p δ和最大最带纹波s δ，则可以使用下面的公式估计其阶数：3．数字滤波器的设计方法：（1） IIR 滤波器设计方法：(a)冲击响应不变法：A. 满足设计要求的模拟原型滤波器)(s H a 进行部分分式展开为： B. 由于 ，可以得到：(b)双线性变换法：A. 设计要求中给出的边界频率进行预畸处理，然后用得到的频率进行模拟滤波器设计，得到模拟原型滤波器)(s H a 。

中国科学院研究生院
试 题 专 用 纸
课程编号： 课程名称：小波与滤波器设计 任课教师：彭思龙
———————————————————————————————————————————————
姓名
学号
成绩
如果 H ( 1) 0, H ( 1) 0 ，再求 a，b，c，d，然后给出相应的高通滤波器。 1 1+2z -1 +4z -2 4、写出下述滤波器 M 相： , 和 。 5 1 1 2 1 az 1 1 z z 6 6 1 e i n ) 利 用 双 尺 度 方 程 求 出 相 应 的 尺 度 函 数 的 Fourier 变 换 5 、 给 定 滤 波 器 H ( ) ( 2 ˆ ( ) 和相应的时间域表示 (t ) ，并试图回答当 n 时 (t ) （能量归一化为 1，并且中心平移到 原点）的极限是什么。
1、 D 为 M 倍的抽取，U 为 L 倍的插值，G(z)为一滤波器，证明下面关系： G z D D G z 和 U G z G z U 2、 已知 FIR 滤波器 H(z) 满足方程 H 2 ( z ) H 2 ( z ) 2 ，求 H(z) 。 3 2 1 2 2 3. 已知低通滤波器 H ( z ) az bz cz d 满足 | H ( z ) | | H ( z ) | 2 ，求 a，b，c，d。又
共 1 页
第
1页

基于小波变换的同态滤波去云方法应用分析杨云龙吴波周小成【摘要】根据遥感影像中云的特性，分析了小波变换去云方法。

选择4种不同的常用小波基和分解层数对去云效果进行分析，并探讨了不用分辨率影像对小波基的敏感性。

以ASTER 影像和IKONOS影像进行实验，认为基于小波变换的薄云去除方法具有较好的效果。

【关键词】小波变换；同态滤波；去云，遥感影像1引言云的去除是遥感影像预处理中重要的一个环节。

目前遥感影像去云的方法主要有多光谱图像的去云[7]、替换法去云[15]、基于数据融合的多传感器遥感影像的去云[17]和同态滤波法去云[1][3][5][6]，其中较为成熟的是同态滤波法。

但传统同态滤波法去云效果不理想，主要存在的不足是：（1）图像经过FFT变换后对高频、低频信息都进行了滤波处理，去云的同时会滤去图像中部分地物信息；（2）快速傅里叶FFT算法计算量巨大，运算速度慢，对图像大小有限制（要求图像的长宽相等且为2的整数幂）。

而小波变换具有较好的分频特性，它将图像分解成高频部分和低频部分，云信息主要集中在低频部分，因此可以只针对低频部分进行处理，而将高频部分直接带入新的结果，这样在去云的同时，既可以最大限度的保持原图像的细节信息，又能减少运算量，大大提高运算速度。

2基于小波变换的同态滤波去云方法2.1 传统同态滤波法同态滤波法是一种把频率过滤和灰度变换结合起来的处理方法，其核心思想是以图像的照明反射模型作为频域处理的基础，根据云覆盖信息在图像频率域上通常占据低频信息的特点，将图像通过快速傅立叶变换转换到频率域，然后使用一种高通滤波器对图像进行空间滤波达到去云目的。

传统同态滤波去云流程如图1：图1传统同态滤波法传统同态滤波去云方法存在的不足是：（1）图像经过FFT变换后对整个的频率域即高频、低频信息都进行了滤波处理，去云的同时会滤去图像中部分地物信息；（2）快速傅里叶FFT 算法计算量巨大，运算速度慢，对图像大小有限制（要求图像的长宽相等且为2的整数幂）。

光学小波变换中的滤波器研究的开题报告一、选题背景光学小波变换是一种基于尺度变换的多分辨率分析方法，对于图像处理、音频信号处理和视频信号处理等领域都有广泛的应用。

滤波器是光学小波变换的核心之一，其作用能影响小波系数的计算结果，从而影响变换后信号的分析效果。

在光学小波变换中的滤波器研究一直是一个被研究的重要问题，如何设计合适的滤波器能够提高小波系数的计算准确性和信号分析效果。

因此，本研究将近一步探讨光学小波变换中滤波器的优化设计和应用。

二、研究目的本研究的主要目的是研究光学小波变换中滤波器的优化设计和应用，以探索其在多分辨率信号分析中的应用价值。

具体目标包括：1. 分析不同滤波器对小波系数计算结果的影响。

2. 探索并优化滤波器设计方法。

3. 研究滤波器在图像处理中的应用效果。

三、研究内容1. 光学小波变换及其滤波器原理研究。

2. 比较不同滤波器对小波系数计算效果的影响。

3. 优化滤波器设计方法，提高小波系数计算准确性。

4. 利用小波分析技术进行图像处理，评估滤波器的应用效果。

四、研究方法1. 文献调研：通过阅读相关文献，了解光学小波变换和滤波器的相关理论以及已有的研究成果。

2. 设计实验：比较不同滤波器的计算效果，并通过实验数据分析不同滤波器的性能优劣。

3. 优化滤波器：基于现有的滤波器设计方法，对其进行改进、优化，以提高小波系数计算精度。

4. 图像处理：利用小波分析技术进行图像处理，通过结果来评估不同滤波器的应用效果。

五、研究意义1. 优化光学小波变换中滤波器设计方法，提高小波系数的计算准确性和信号分析效果。

2. 探索滤波器在多分辨率信号分析领域中的应用价值。

3. 为图像处理提供一种新的思路和方法，为图像分析和处理提供帮助。

六、研究计划本研究的时间预计为一年，预计工作计划如下：1. 第一季度：阅读相关文献，掌握光学小波变换和滤波器的原理，分析不同滤波器对小波系数计算的影响。

2. 第二季度：进行实验设计，比较不同滤波器的性能。

双正交小波滤波器组的提升构造与优化
王海涛;丁宣浩
【期刊名称】《计算机工程与应用》
【年(卷),期】2010(046)008
【摘要】AK编码增益的角度,考察了双通道双正交小波图像编码系统的性能.首先,对双正交滤波器组的多相位矩阵进行提升分解,并结合消失矩和归一化条件,得到了含自由变量的提升参数.根据Vaidyanathan编码增益表达式求出编码增益的最优值.然后重点构造了三种9/7小波.尽管MIT小波的图像压缩质量略低于CDF 9/7小波,但它不仅系数简单,易于硬件实现,而且编码增益更大.这在编码器设计时具有重要实用价值.
【总页数】4页(P137-140)
【作者】王海涛;丁宣浩
【作者单位】桂林电子科技大学,数学与计算科学学院,广西,桂林,541004;桂林电子科技大学,数学与计算科学学院,广西,桂林,541004;重庆工商大学,数学与统计学院,重庆,400067
【正文语种】中文
【中图分类】TN911
【相关文献】
1.基于提升格式的双正交小波构造 [J], 耿艳峰;冯叔初;郑金吾
2.构造双正交小波的提升框架方法研究 [J], 牛全营;王世雷
3.11-9双正交小波的构造与提升分解 [J], 杨建湘
4.FIR完全重建滤波器组构造双正交小波基 [J], 熊小兵;赵尔沅
5.双正交小波的提升构造研究 [J], 陈智能;高协平
因版权原因，仅展示原文概要，查看原文内容请购买。

1 1 H 1 z G1 z z H 1 z G1 z z 2 2 1 H 0 z G0 z H 1 z G1 z z 2 1 H 0 z G0 z H 1 z G1 z z 2
n
G1 z z l H 0 z , 即g1 n 1 h0 n l
n
• •
•
这意味着 g 0 , h1 间及 g1 , h0 间满足下述关系。 ~ n, g ~ n 分别为 令 g g1 n, g 0 n 的首尾倒置， 1 0 则有 当 l 为奇数时： ~ g 0 n 2i , h1 n 2 j 0 ~ n 2i , h n 2 j 0 g
2.为使成为的延迟，纯延迟项应为纯延迟，即：
H 0 z G0 z H1 z G1 z cz
k
• •
1.抗混迭条件。 为使混迭项为零，常令分析滤波器与综合滤 波器间满足下述交叉关系：
G0 z z l H 1 z , 即g 0 n 1 h1 n l
1 0
• 当l
~ h g • 即 l 为奇数时， 与 的偶数移位交叉正交； ~ g h 当 l 为偶数时， 与 的奇数移位交叉正交， 称双正交关系。
~ n 2i 1, h n 2 j 0 g 1 为偶数时： 0 ~ n 2i 1, h n 2 j 0 g 1 0
小波变换与滤波器组
4.1 双通道多采样率滤波器组及其理想 重建条件
• • 一. 两个基本关系 1．
•
2．易位
•
因此得到下列等价关系
•
二. 双通道多采样率系统
Gi z 为合成滤波器。 • 图中H i z 为分析滤波器，

第九章 小波理论及小波滤波去噪方法
9.2.2连续小波变换
§ 9.2.小波变换
第21页，共28页。
*
(2) 缩放。就是压缩或伸展基本小波， 缩放系数越小， 则小波越窄
第九章 小波理论及小波滤波去噪方法
9.2.2连续小波变换
§ 9.2.小波变换
第22页，共28页。
*
第九章 小波理论及小波滤波去噪方法
§ 9.1 从傅里叶变换到小波分析
第11页，共28页。
第九章 小波理论及小波滤波去噪方法
由此可见，STFT虽然在一定程度上克服了标准傅里叶变换不具有时域局部分析能力的缺陷，但他也存在着自身不可克服的缺陷——其时间频率窗口是固定不变的，一旦窗口函数选定其时频分辨率也就确定了。而时间和频率的最高分辨率受制约，任一方分辨率的提高都意味着另一方分辨率的降低。 可以说STFT实质上是具有单一分辨率的信号分析方法，若要改变分辨率，则必须重新选择窗口函数g(t)。 因此STFT用来分析平稳信号犹可，但对非平稳信号，在信号波形变化剧烈的时刻，主频是高频，要求有较高的时间分辨率，即δ要小，而波形变化比较平缓的时刻，主频是低频，则要求有较高的频率分辨率，ε要小，而STFT不能兼顾二者。
(3) 平移。小波的延迟或超前。在数学上,函数f(t)延迟k的表达式为f(t-k)，
(a) 小波函数ψ(t)； (b) 位移后的小波函数ψ(t-k)
9.2.2连续小波变换
§ 9.2.小波变换
第23页，共28页。
*
（4）小波变换的步骤: 第一步： 取一个小波与信号的最前面部分比较; 第二步： 计算相关因子C,C代表小波和这段数据的相关性 即:C越大,两者越相似;
（1）继承和发展了STFT的局部化思想。 （2）克服了窗口大小不随频率变化、缺乏离散正交基的缺点。

∞
ϕ(t − m)ϕ(t − n) dt = δm,n .
−∞
Hence
∞
f 2 (t) dt =
−∞ n∈Z
f 2 [n].
Therefore if f (t) ∈ L2 then f [n] ∈
2
and vice-versa.
(b) P ROBLEM 5. Since V0 ⊂ V1 and f ∈ V0 and g ∈ V1 , g − f ∈ V1 . Clearly, g − f ∈ / W1 in general since V1 ⊕ W1 = V2 which means that the only element common between V1 and W1 is the 0 function. However, it is also true in general that g − f ∈ / W0 . This is because any element g ∈ V1 can be uniquely written as g = g1 + g2 ⇒ g − f = g1 − f + g2 .
18.327/1.130: Wavelets, Filter Banks and Applications Solutions to Problem Set 3
M ARK D ISTRIBUTION P ROBLEM 6.1.3 6.1.5 6.2.7 6.2.8 6.3.2 6.3.3 6.4.4 6.5.4 6.5.7 6.5.9 7.1.8 7.2.2 7.3.7 7.3.8 7.5.4 T OTAL G RADING P OLICY • A reasonable attempt to answer a one-mark question fetched half-marks • Problems not attempted fetched no marks. • Since lifting was not covered before the problem set was due, Problem 6.5.7 was converted into a one-mark bonus question. M ARKS 1.0 0.5 1.0 1.0 0.5 0.5 1.0 0.5 B ONUS 1.0 1.0 0.5 0.5 0.5 0.5 10.0

维普资讯
第３ 卷第 ７ ５ 期
２ ０ 年 ７Biblioteka ０８ 光 电工程 Ｏｐ ｏ Ｅ ｅ ｔｏ ｉ ｇ ｎ ｅ ｉ ｇ ｔ — ｌｃ ｒ ｎ ｃＥｎ ｉｅ ｒ ｎ
Ｖ０ｌ ５． － ３ Ｎｏ． ７ Ｊ ｌ， ０ ｕ ｙ ２ ０８
文 章编 号 ：１ ０ — ０ Ｘ（０ ８０ — １９ ０ ０ ３ ５ １ ２ ０ ）７ ０ ０ — ７
ｗａ ｅｅ ａ ｅ ｒ ｓ ａ ｌ ｉ ｅ ｅ ｔａ ｄ ｔ ｅ ｗａ ｅｅ ａ ｅ ｏ ｅ ｍｉ ｉ ｍ ｕ ｎ ｉａｉ ｎ ｅ ｏ ｎ ｓ ａ ｅ ａ ｄ ｆｅ ｕ ｎ ｙ ｖ ｌｔｂ ｓ ｓ ａ ｅ ｕ ｕ ｌ ｄ ｆ ｒ ｎ ｎ ｈ ｖ ｌｔｂ ｓ ｆ ｔ ｎ ｍｕ ｑ ａ ｔ ｔ ｒ ｒ ｉ ｐ ｃ ｎ ｒ ｑ ｅ ｃ ｙ ｈ ｚ ｏ ｄ ｍａｎ ｉ ／ ｖ ｌ ｔ ｆｅ ｘ ｈ ｎ ｉ ｇ ｔ ｅ ｄ ｃ ｍｐ ｓｔ ｎ ａ ｄ ｒ ｃ ｎ ｔｕ ｔ ｎ ｆ ｔ ｒ ． ｃ ｒ ｉ ｇ ｔ ｈ ｅ ｓ ｑ ａ ｔ ａｉ ｎ ｏ ｉ ｓ ５３ ｗａ ｅｅ ｔｒｅ ｃ ａ ｇ ｎ ｈ ｅ ｏ ｏ ｉ ｏ ｎ ｅ ｏ ｓ ｃ ｉ ｌ ｓ Ａｃ ｏ ｄ ｎ ｏ ｔ ｅ ｌａ ｔ ｕ ｎ ｉ ｔ ａ ｉ ｒ ｏ ｉ ｅ ｚ ｏ ｅ ｏ ｒ ｅ ｏ ｆｏ ｔ ａ ｖ ｌｔ ｌ ｒ ｎ ｓ ａ ｅｄ ｍａ ｎ ａ ｄ ｆｅ ｕ ｎ ｙ ｄ ｗ ￣ｎ ａ ｐ ｉ ｌ ｖ ｌ ｔ ｓｃ ｎ ｔ ｃｅ ａ ｅ ｒ ｒｃ ｔ ｒ ｎ ｏ ｐ ｉ ｌ ｉ ｉ ｃ ｗａ ｅｅ ｔ ｐ ｃ ｏ ｉ ｎ ｒ ｑ ｅ ｃ ｏ ．ｉ ， ｎ ｏ ｔ ｉ ｆ ｅｉ ｍａ ｗａ ｅ ｅ ｏ ｓｒ ｔｄ ｂ ｓ ｄ ｗａ ｕ ｏ ｉ ｉ ｇ ａ ｇ ｒ ｈ ｎ ｌ ｔ ｌ ｏ ｔ ｍ． ｆｎ ｉ Ｋｅ ｒ ｓ ｐ ｉ ａ ｖ ｌｔｆ ｔｒ ｑ ａ ｔ ａｉ ｎ ｅ ｏ ； ｉ ｉ ｇ ａ ｇ ｒ ｍ ； ｐ ｉ ｌｗａ ｅ ｅ；ｓ ａ ｅ ｄ ｍａ ｎ ａ ｄ ｆｅ ｕ ｎ ｙ ｙ ｗｏ ｄ ：ｏ ｔｃ ｌ ｗａ ｅｅ ｌ ； ｕ ｎ ｉ ｔｏ ｒ ｒ ｌ ｎ ｌ ｏ ｔ ｉ ｅ ｚ ｔ ｆ ｉ ｈ ｏｔ ｍａ ｖ ｌｔ ｐ ｃ ｏ ｉ ｎ ｑ ｅ ｃ ｒ

一种基于小波理论的滤波器的设计段炼（哈尔滨工业大学电气工程系，黑龙江哈尔滨 150001）摘要：本文以实际问题为背景，为了解决在外界干扰的下，传感器检测到信号带有噪声的问题，提出了利用小波变换将信号分解，利用加权阈值消除噪声，再将信号重构的方法。

为了更好地消除伪吉布斯现象，还使用了平移变换平移算法（cycle spinning）。

关键词：滤波器；小波变换；平移变换平移；阈值滤波1.引言在控制系统中，我们常常需要精确地测得系统的信号，以便进行精确控制。

在实际工程中，由于外界干扰，以及传感器自身原因，传感器检测出来的信号常常会带有噪声。

传统的噪声滤波方法无一不是根据Fourier分析理论,由此衍生出许多滤波的算法。

这些算法一般依靠调整滤波器的通频带进行设计。

傅里叶分析用的是全局变换，故不能描述信号的时频局域性，因此这些方法具有一定的局限性。

近年来小波变换在理论和应用上的研究都取得了显著成绩,由于小波变换具有优良的时频局部化的特点,小波分析己成为非线性、非平稳性信号处理很好的数学工具[1]。

2.理论原理2.1 小波变换原理小波，即小区域的波。

小波函数的定义是:设ψ(t)为一平方可积函数，即ψ(t) ∈L2(R),若其傅立叶变换满足条件：2() R dψωωω<∞⎰(2-1) 则称ψ(t)为一个基本小波。

并称式(2-1)为小波函数的可容许性条件。

小波函数ψ(t)常被称为母小波，因为对其作平移、伸缩可以得到一族小波函数。

,()(),0,a bt bt a b Raψ-=>∈(2-2) 一般是时域上以t=b为中心的带通函数，在时域和频域都具有局部化（紧支撑）。

其中a为尺度因子，b为位移因子。

函数f(t)的连续小波变换形式可以写成：,(,)()()f a bW a b f t t dtψ+∞-∞=⎰(2-3) f(t)∈L2(R)，ψ(t)为容许性小波。

基函数,()a btψ的两个参数a和b均为连续变量。

局部小波谱分析与滤波算法在信号处理中的应用研究随着科技的不断进步，信号处理技术在各个领域得到了广泛的应用，其中局部小波谱分析与滤波算法是一种常用的信号处理方法。

它能够高效地处理信号，并提取出信号中的有用信息，具有重要的应用价值。

本文将重点介绍局部小波谱分析与滤波算法的原理、算法流程及其在信号处理中的应用研究。

一、局部小波谱分析与滤波算法原理局部小波谱分析与滤波算法是一种基于小波分析的非平稳信号分析方法，它通过将小波分析和信号滤波相结合，可以将信号分解为不同的频带，同时保留信号的时域和频域信息。

在局部小波谱分析与滤波算法中，首先利用小波分析将原始信号分解为不同尺度的小波系数，然后通过设置特定的窗口大小，在每个小波系数的局部区域内进行分析，最终得到局部小波谱。

在局部小波谱分析中，主要的目的是研究信号在不同频段上的分布情况，进而进行信号滤波的处理。

根据局部小波谱分析结果，可以采用不同的滤波算法来对信号进行滤波处理，去除噪声和干扰，提高信号的质量和精度。

二、局部小波谱分析与滤波算法流程局部小波谱分析与滤波算法具体流程如下：1. 信号采样：将原始信号通过采样器获取到离散的信号。

2. 小波分解：将离散信号进行小波分解，得到不同尺度的小波系数。

3. 均值计算和正则化：对每个小波系数在局部窗口内进行均值计算，并进行正则化处理。

4. 局部小波谱估计：利用小波系数的局部均值和正则化系数来估计局部小波谱，并计算出信号在每个频带上的能量分布。

5. 信号重构和滤波：根据局部小波谱估计结果，采用不同的滤波算法进行信号重构和滤波，去除噪声和干扰，得到干净的信号。

三、局部小波谱分析与滤波算法在信号处理中的应用研究局部小波谱分析与滤波算法在信号处理领域具有广泛的应用，可以用于信号去噪、事件检测、特征提取等方面。

下面将具体介绍其在不同领域的应用。

1. 生物医学信号处理生物医学信号处理中常常遇到信号质量低、干扰多的问题，局部小波谱分析与滤波算法可以有效地提高信号质量和精度。

小波变换码中滤波器的选择
长沙国防;沙基昌
【期刊名称】《信号处理》
【年(卷),期】1998(14)A12
【摘要】在本文中，我们从广义编码增益、分解重构性能与对误差的敏感性、编码性能与主观质量三个方面对双正交小波１２／４、９／７与９／３进行比较，得出：双正交小波１２／４比９／７与９／３更适合于小波图像压缩，特别是在高保真压缩中；在低比特率编码中，双正交小波１２／４与９／７相差不大。

【总页数】6页(P27-32)
【作者】长沙国防;沙基昌
【作者单位】科技大学系统工程与数学系;科技大学系统工程与数学系
【正文语种】中文
【中图分类】TN919.8
【相关文献】
1.基于离散超小波变换的光码正交码 [J], 吴寿章;刘平
2.小波变换在并联型有源电力滤波器中的应用 [J], 赵卫东;葛芦生
3.小波变换在有源电力滤波器谐波分析中的应用 [J], 梁东莺;毛蔚
4.小波变换中滤波器构造和零延拓的研究比较 [J], 宋长虎
5.小波变换域自适应滤波器在传动误差测试中的应用 [J], 唐进元;李松
因版权原因，仅展示原文概要，查看原文内容请购买。

胶片薄膜光学小波滤波器的研究及其实现的开题报告题目：胶片薄膜光学小波滤波器的研究及其实现开题报告一、研究背景及意义胶片薄膜是一种具有可调性、可控性和可重复性的光学薄膜材料，广泛应用于激光技术、太阳能电池、显示技术等领域。

其中，薄膜滤波器作为胶片薄膜应用的主要形式之一，具有很高的应用价值。

然而，传统的滤波器设计方法需要进行复杂的光学设计和实验验证，成本高、效率低，不适合大规模生产。

因此，我们需要一种便捷、高效的滤波器设计方法，以提高滤波器的设计、制备和性能调控的效率和精度。

近年来，小波分析作为一种多尺度的信号分析方法，已经被广泛应用于图像处理、信号处理、音频处理等领域。

相比于传统的滤波器设计方法，小波滤波器设计方法具有更高的效率、更好的精度和更灵活的性能调控方式，并且可以与胶片薄膜材料的制备过程相结合，形成一种全新的胶片薄膜光学小波滤波器设计方法。

因此，本研究将采用小波分析方法，结合胶片薄膜制备技术，设计、制备和测试一种胶片薄膜光学小波滤波器，并对其性能和应用进行分析和实验验证，以探索一种新型滤波器的设计方法，为光学滤波器的研究和应用提供新的思路和方法。

二、研究内容（1）胶片薄膜光学小波滤波器的设计原理和方法本研究将采用小波分析原理，结合胶片薄膜的制备技术，设计一种胶片薄膜光学小波滤波器。

首先构建具有多尺度的小波基函数，利用小波变换对滤波器进行分析和设计，以实现对滤波器频率响应的调控。

然后结合胶片薄膜材料的物理学特性和制备工艺，实现对滤波器的制备和性能调控。

（2）胶片薄膜光学小波滤波器的制备和测试本研究将采用物理气相沉积法制备胶片薄膜滤波器，对制备过程中的各种参数进行优化和控制，从而得到具有高质量和重复性的胶片薄膜样品。

然后利用白光干涉法、矢量网络分析仪等实验设备对样品进行测试，分别对滤波器波长选择性、透射率、反射率等性能参数进行测量和分析。

（3）胶片薄膜光学小波滤波器的性能和应用分析本研究将通过对胶片薄膜光学小波滤波器的性能和应用进行分析和评价，从而确定滤波器的优点和局限性，并探索滤波器在光学器件、激光技术、太阳能电池等领域中的应用前景。