二次函数中的符号问题专题复习

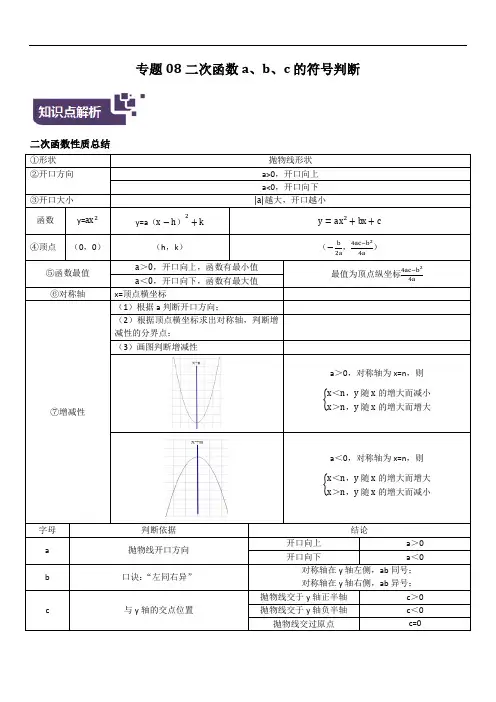
专题08二次函数a、b、c的符号判断二次函数性质总结（3）画图判断增减性判断依据判断下列图像对应的a，b，c的正负：图像字母符号（“正”或“负”）a b c a b c a b c a b c a b1．已知二次函数2y ax bx c =++的图象如图所示，则( )A ．0,0b c >>B ．0,0b c ><C ．0,0b c <<D ．0,0b c <>2．同一平面直角坐标系中，抛物线y ＝(x －a )2与直线y ＝ax +a 的图象可能是（ ）A ．B ．C ．D ．3．在同一平面直角坐标系中，函数y ＝ax 2＋b 与y ＝ax ＋b （ab ≠0）的大致图象可能是（ ）A ．B ．C ．D ．4．如图,在同一直角坐标系中, y ax c =+与2y ax c =+的图象为( )A ．B ．C ．D ．5．在同一坐标系中，一次函数2y mx n =-+与二次函数2y x m =+的图象可能是（ ）．A ．B ．C ．D ．6．如图，在同一坐标系下，一次函数y ax b =+与二次函数24y ax bx =++的图像大致可能是（ ）A ．B ．C ．D ．7．在同一坐标系中，一次函数y =ax +b 与二次函数y =ax 2+b 的大致图象为（ ）A ．B ．C ．D ．8．函数y kx b =+与2y kx b =+的图像大致为（ ）A ．B ．C ．D ．9．二次函数y ＝ax 2与一次函数y ＝ax+a 在同一坐标系中的图象大致为( )A ．B ．C ．D ．10．已知抛物线2y ax bx =+和直线y ax b =+在同一坐标系内的图象如图所示，其中正确的是（ ）11．在同一坐标系中表示2y ax =和()0y ax b ab =+>的图象的是( )A ．B ．C ．D ．12．在同一平面直角坐标系中，一次函数y ）ax +b 和二次函数y ）ax 2+bx +c 的图象可能为（ ）A ．B ．C ．D ．13．已知函数y 1＝mx 2+n ，y 2＝nx +m （mn ≠0），则两个函数在同一坐标系中的图象可能为（ ）A ．B ．C ．D ．14．已知一次函数y=ax+b 与二次函数y=ax 2+bx,它们在同一坐标系内大致图象是（ ）A ．B ．C ．D ．15．函数y=ax 2+ax+a）a≠0）的图象可能是下列图象中的（ ）A ．B ．C ．D ．16．二次函数2y ax ＝与一次函数y ax a ＝在同一坐标系中的大致图象可能是（ ）A ．B ．C ．D ．17．函数y=a 2x ＋c 与y=-ax ＋c(a≠0)在同一坐标系内的图像是图中的（ ）A ．B ．C ．D ．18．在同一坐标系中，函数y=ax 2与y=ax ﹣a （a≠0）的图象的大致位置可能是（ ）A ．B ．C ．D ．19．在同一平面直角坐标系中，若正比例函数(0)y mx m =≠）y 随x 的增大而减小，则它和二次函数2y mx m =+的图象大致是） ）20．在同一坐标系中，一次函数y=ax+1与二次函数y=x 2+a 的图像可能是（ ）A ．B ．C ．D ．21．在同一直角坐标系中y=ax 2+b 与y=ax+b）a≠0）b≠0）图象大致为（ ）A．B．C．D．。

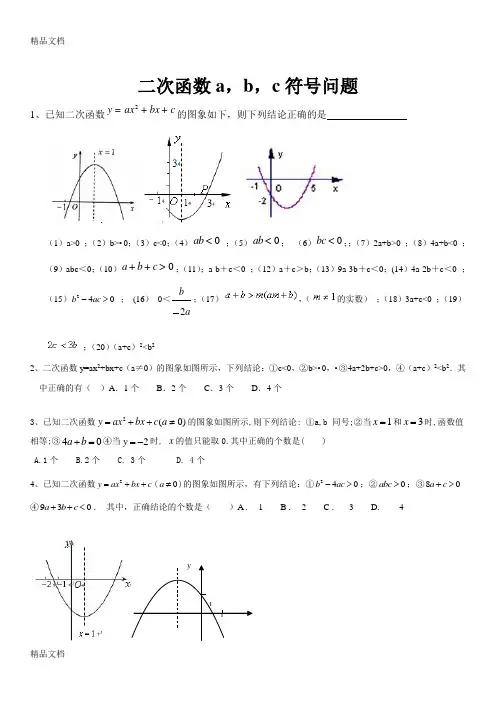
精品文档二次函数a ，b ，c 符号问题1、已知二次函数2y ax bx c =++的图象如下，则下列结论正确的是（1）a>0 ；（2）b>•0；（3）c<0；（4）0ab < ；（5）0ab <； （6）0bc <；；（7）2a+b>0 ；（8）4a+b<0 ；（9）abc ＜0；（10）0a b c ++>；（11）；a-b ＋c ＜0 ；（12）a ＋c ＞b ；（13）9a-3b ＋c ＜0；(14）4a-2b ＋c ＜0 ；（15）240b ac -> ； (16） 0＜a b 2；（17），（的实数） ；（18）3a+c<0 ；（19）；（20）（a+c ）2<b 22、二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，下列结论：①c<0，②b>•0，•③4a+2b+c>0，④（a+c ）2<b 2．其中正确的有（ ）A ．1个 B ．2个 C ．3个 D ．4个3、已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论: ①a,b 同号;②当1x =和3x =时,函数值相等;③40a b +=④当2y =-时, x 的值只能取0.其中正确的个数是( )A.1个B.2个C. 3个D. 4个4、已知二次函数2y ax bx c =++(0a ≠)的图象如图所示，有下列结论：①240b ac ->；②0abc >；③80a c +> ④930a b c ++<． 其中，正确结论的个数是（ ）A . 1 B . 2 C . 3 D . 411O y精品文档 5、已知二次函数2y ax bx c =++的图象如图所示，有以下结论：①0a b c ++<；②1a b c -+>；③0abc >；④420a b c -+<；⑤1c a ->其中所有正确结论的序号是（ ）A ．①②B ． ①③④C ．①②③⑤D ．①②③④⑤。

二次函数a、b、c、△符号问题及相关问题一选择题1.如图所示，抛物线的图象则下列结论正确的是（）A a<0，b<0，c＞0，b2＜4acB a<0，b>0，c<0，b2＜4acC a<0，b>0，c＞0，b2>4acD a>0，b<0，c＞0，b2>4ac2.如图a＜0，c＞0那么y＝ax2＋bx＋c的图象是（）3.已知二次函数y=ax2+bx+c (a≠0）的图象如图所示，则下列结论：①a、b同号；②当x=1和x=3时，函数值相等；③ 4a+b=0；④当y=－2时，x的值只能取0．其中正确的个数是（）A l个 B 2个 C 3个 D 4个4.二次函数y=mx2+2mx-（3-m）的图象如图所示，则m的取值范围是（）A m＜3B m＞3C m＞0D 0＜m＜35.在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )6.已知抛物线y=x2+bx+c的部分图象如右图所示，若y<0，则x的取值范围是（）A −1<x<4B -1<x<3C x<-1或x>4D x<-1或x>37.在某次投篮中，球的运动路线是y=-0.2x2+3.5的一部分(如图)，若命中篮圈中心，则他与篮底的距离为( )A 3.5mB 4mC 4.5mD 4.6m8.若抛物线y=x2+8x+h2的顶点在x轴上，则（）A h=0 B h=±16 C h=±4 D h=49.如果二次函数y=ax2+m的值恒大于0，那么必有（）A a＞0，m取任意实数B a＞0，m＞0C a＜0，m＞0D a，m均可取任意实数10.已知a-b+c=0，9a+3b+c=0，则抛物线y=ax2+bx+c的顶点可能在( )A 第一或二象限B 第三或四象限C 第一或四象限D 第二或四象限11.抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），且满足4a+2b+c＞0，以下结论：①a+b＞0；②a+c＞0；③﹣a+b+c ＞0；④b2﹣2ac＞5a2，其中正确的个数有（）A．1个B．2个C．3个D．4个12.物线y=ax2+bx+c(a≠0)全部图象都在x轴下方，则( )A a>0，b2-4ac≥0B a>0，b2-4ac<0C a>0，b2-4ac≥0D a<0，b2-4ac<0二填空题13.若二次函数y=(a-1)x2-2x+1的图象与x轴只有一个交点，则a=________14.不论x取什么实数，y=2x2-6x+m的图象都在x轴的上方，那么m的取值范围是________；y=mx2－3x＋2m－m2的图象经过原点，则m＝15.二次函数y＝x2-(m-4)x+9的图象的顶点在y轴上，则m＝16.二次函数y＝x2＋2kx＋8的顶点在x轴上，则k＝17.已知抛物线y＝x2－2（k+1）x＋16的顶点在x轴上，则k的值为______18.抛物线y＝x2－(m－4)x－m与x轴的两个交点关于y轴对称，其顶点坐标为______19.已知抛物线y＝x2+2（m－3）x＋1的顶点在x轴上，则m＝______顶点坐标是_________20.平移抛物线y = x2+2x-8，使它经过原点，写出平移后抛物线的一个解析式21.如果二次函数y=x2-3x-2k,不论x取任何实数,都有y>0,则k的取值范围是________22.把抛物线y=2(x+1)2向下平移______单位后,所得抛物线在x轴上截得的线段长为523.抛物线y=-3(x+2)2的顶点坐标是_____________,若将它旋转180后得新的抛物线,其解析式为____________________24.把y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2-3x+5,则有b=_____，c=_____三解答题25.如图，抛物线y＝ax2+bx＋c确定a，b，c，b2-4ac，a+b+c，a-b+c的符号26.抛物线y＝ax2+bx＋c的图像如图，对称轴是直线x＝－1确定a,b,c，Δ及a－b＋c 的符号27.已知抛物线y＝ax2+bx+c的一段图象如图所示．（1）确定a、b、c的符号；（2）求a+b+c的取值范围．28.如图为二次函数y=ax2＋bx＋c的图象，在下列说法中：①ac＜0；②方程ax2＋bx＋c=0的根是x1= －1, x2= 3；③a＋b＋c＞0；④当x＞1时，y随x的增大而增大.正确的说法有_____________29.有一个抛物线形的桥洞，桥洞离水面的最大高度BM为3米，跨度OA为6米，以OA所在直线为x轴，O为原点建立直角坐标系（如图所示）．（1）请你直接写出O、A、M三点的坐标；（2）一艘小船平放着一些长3米，宽2米且厚度均匀的矩形木板，要使该小船能通过此桥洞，问这些木板最高可堆放多少米（设船身底板与水面在同一平面）？30.如图，二次函数y=x2+bx+c的图象经过点M（1，—2）、N（—1，6）.（1）求二次函数的关系式；（2）把Rt△ABC 放在坐标系内，其中∠CAB=900，点A、B的坐标分别为（1，0）、（4，0），BC = 5，将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离.二次函数a、b、c、△符号问题及相关问题答案1.C2.D3.B4.D5.B6.B7.B8.C9.B 10.C 11.D 12.D11.分析（1）因为抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），把点（﹣1，0）代入解析式，结合4a+2b+c＞0，即可整理出a+b＞0；（2）②+①×2得，6a+3c＞0，结合a＜0，故可求出a+c＞0；（3）画草图可知c＞0，结合a﹣b+c ＝0，可整理得﹣a+b+c＝2c＞0，从而求得﹣a+b+c＞0；（4）把（﹣1，0）代入解析式得a﹣b+c＝0，可得出2a+c＞0，再由a＜0，可知c＞0则c﹣2a＞0，故可得出（c+2a）（c﹣2a）＞0，即b2﹣2ac﹣5a2＞0，进而可得出结论．解：（1）因为抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），所以原式可化为a﹣b+c＝0 ①，又因为4a+2b+c＞0 ②，所以②﹣①得：3a+3b＞0，即a+b＞0；（2）②+①×2得，6a+3c＞0，即2a+c＞0，∴a+c＞﹣a，∵a＜0，∴﹣a＞0，故a+c＞0；（3）因为4a+2b+c＞0，可以看作y＝ax2+bx+c（a＜0）当x＝2时的值大于0，草图为：可见c＞0，∵a﹣b+c＝0，∴﹣a+b﹣c＝0，两边同时加2c得﹣a+b﹣c+2c＝2c，整理得﹣a+b+c＝2c＞0，即﹣a+b+c＞0；（4）∵过（﹣1，0），代入得a﹣b+c＝0∴b2﹣2ac﹣5a2＝（a+c）2﹣2ac﹣5a2＝c2﹣4a2＝（c+2a）（c﹣2a）又∵4a+2b+c＞04a+2（a+c）+c＞0，即2a+c＞0①，∵a＜0，∴c＞0则c﹣2a＞0②，由①②知（c+2a）（c﹣2a）＞0，所以b2﹣2ac﹣5a2＞0，即b2﹣2ac＞5a2,综上可知正确的个数有4个．故选：D．13.2 14.m＞9／2，2 15.4 16.±22 17.3或-5 18.（0，-4） 19.4或2，（1,0）或（-1,0） 20.y=x2+2x 21.k＜-9／8 22. 25／2 23.（-2,0），y=3（x+2）2 24.3，725. a＜0，b＞0，c＞0，b2-4ac＞0，a+b+c＞0，a-b+c＜026.a＜0，b＜0，c＞0，△＞0，a-b+c＞027.解：（1）根据抛物线开口向上，则a＞0，∵对称轴在x轴正半轴可知﹣＞0，∴b＜0，又与y轴交点在y轴负半轴，∴c＜0，故a＞0，b＜0，c＜0；（2）∵抛物线y＝ax2+bx+c过点（﹣1，0），（0，﹣1），∴a﹣b+c＝0，c＝﹣1，即a﹣b＝1，a＝b+1，∴a+b+c＝b+1+b﹣1＝2b，∵b＜0，∴2b＜0，∵a＞0，∴b+1＞0，∴b＞﹣1，2b＞﹣2，故，﹣2＜a+b+c＜0．28.①②④29.解：（1）解：如图，O（0，0）．∵OA为6米，∴A（6，0），又∵BM的对称轴，BM为3米，∴M（3，3）．综上所述，O（0，0），A（6，0），M（3，3）．（2）设抛物线的关系式为y＝a（x﹣3）2+3，因为抛物线过点（0，0），所以0＝a（0﹣3）2+3，解得a＝﹣，所以y＝﹣（x﹣3）2+3＝﹣x2+2x，要使木板堆放最高，依据题意，得B点应是木板宽CD的中点，把x＝2代入y＝﹣x2+2x，得y＝，所以这些木板最高可堆放米．30.解：（1）∵M（1，﹣2），N（﹣1，6）在二次函数y＝x2+bx+c的图象上，∴，解得二次函数的关系式为y＝x2﹣4x+1．（2）Rt△ABC中，AB＝3，BC，＝5，∴AC＝4，4＝x2﹣4x+1，x2﹣4x﹣3＝0，解得（负值不合题意舍去），∵A（1，0），∴点C落在抛物线上时，△ABC向右平移（1+）个单位．。

二次函数中的符号问题(°、b、C、△等符号)预习案回顾知识点：1、抛物线y=ax1+bx+c的开口方向与有关；2、抛物线y=αv2+bx+c与y轴的交点是；3、抛物线y=ax2+bx+c的对称轴是；总结：抛物线产加+法+c的符号问题：(1)。

的符号：由抛物线的开口方向确定开口向上：a>0；开口向下：«<0(2)c的符号：由抛物线与)，轴的交点位置确定：交点在X轴上方：OO；交点在X轴下方：c<0；经过坐标原点：C=O(3)b的符号：由对称轴的位置确定：对称轴在y轴左侧：a、b同号；对称轴在y轴右侧：4、b异号;对称轴是)，轴：b=0简记为：左同右异(4)从-4"的符号：由抛物线与X轴的交点个数确定：与X轴有两个交点：b2-4ac>0i与X轴有一个交点：b2-4ac=0↑与X轴无交点：b2-4ac<0(5)α+Hc的符号：由X=I时抛物线上的点的位置确定(6)Q-Hc的符号：由X=T时抛物线上的点的位置确定探究案探究一抛物线y=0x2+bx+c如图所示，试确定〃、b、c、△的符号：练一练：1.二次函数y=αχ2+"+C•的图象如图所示，则一次函数y=bx+4的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限2.已知抛物线)，=加+公+c(WO)在平面直角坐标系中的位置如图所示，则下列结论中正确的是( )A.aX)B.b<0C.CyOD.α+b+c>O3.已知二次函数y=αf+加+c(αwθ)的图象如图，对称轴为“=_1下列结论中正确24 .如图所示的二次函数y="?+云+c 的图象中，刘星同学观察得出了下面四条信息:6.如图是二次函数），=如2+"+°（。

=0）在平面直角坐标系中的图象，根据图形判断：①c >0；②a+b+c <0；③2a-b <0；b 2+Sa>4ac .其中正确的是（填写序1Q的函数的一些结论：①当机=-3时，函数图象的顶点坐标是（1-）；②当m>033时，函数图象截X 轴所得的线段长度大于∙∣;③当机<0时，函数在时，），随X 的增大而减小；④当小声0时，函数图象经过同一个点.其中正确的结论有（ ） A.®®®®B.①®® C.①③④D.®®9.已知二次函数y=f1√+∕λx +c 的图象如图所示，有以下结论：①a+Z?+c<0；②α-b+c>1：③H?c>0；④4Q -2Z J +C <0；⑤。