二次函数中abc的符号问题

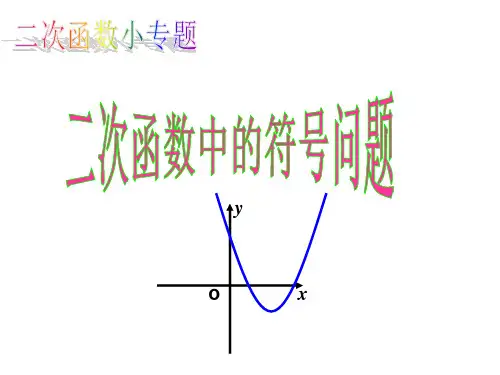
二次函数系数a、b、c与图像的关系知识要点二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2-4ac的符号由抛物线与x轴交点的个数确定：2个交点，b2-4ac＞0；1个交点，b2-4ac=0；没有交点，b2-4ac＜0．（5）当x=1时，可确定a+b+c的符号，当x=-1时，可确定a-b+c的符号．（6）由对称轴公式x=，可确定2a+b的符号．一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．42．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．45．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜37．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个10、（2011?重庆）已知抛物线y=ax2+bx+c（a≠0）在平面直角坐标系中的位置如图所示，则下列结论中，正确的是（）A、a＞0B、b＜0C、c＜0D、a+b+c＞011、（2011?雅安）已知二次函数y=ax2+bx+c的图象如图，其对称轴x=-1，给出下列结果①b2＞4ac；②abc＞0；③2a+b=0；④a+b+c＞0；⑤a-b+c＜0，则正确的结论是（）A、①②③④B、②④⑤C、②③④D、①④⑤12、（2011?孝感）如图，二次函数y=ax2+bx+c的图象与y轴正半轴相交，其顶点坐标为（12，1），下列结论：①ac＜0；②a+b=0；③4ac-b2=4a；④a+b+c＜0．其中正确结论的个数是（）A、1B、2C、3D、4答案一．选择题（共9小题）1．（2014?威海）已知二次函数y=ax2+bx+c（a≠0）的图象如图，则下列说法：①c=0；②该抛物线的对称轴是直线x=﹣1；③当x=1时，y=2a；④am2+bm+a＞0（m≠﹣1）．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：抛物线与y轴交于原点，c=0，（故①正确）；该抛物线的对称轴是：，直线x=﹣1，（故②正确）；当x=1时，y=a+b+c∵对称轴是直线x=﹣1，∴﹣b/2a=﹣1，b=2a，又∵c=0，∴y=3a，（故③错误）；x=m对应的函数值为y=am2+bm+c，x=﹣1对应的函数值为y=a﹣b+c，又∵x=﹣1时函数取得最小值，∴a﹣b+c＜am2+bm+c，即a﹣b＜am2+bm，∵b=2a，∴am2+bm+a＞0（m≠﹣1）．（故④正确）．故选：C．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．2．（2014?仙游县二模）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给出以下结论：①a+b+c＜0；②a﹣b+c ＜0；③b+2a＜0；④abc＞0．其中所有正确结论的序号是（）A．③④B．②③C．①④D．①②③考点：二次函数图象与系数的关系．专题：数形结合．分析：由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①当x=1时，y=a+b+c=0，故①错误；②当x=﹣1时，图象与x轴交点负半轴明显大于﹣1，∴y=a﹣b+c＜0，故②正确；③由抛物线的开口向下知a＜0，∵对称轴为0＜x=﹣＜1，∴2a+b＜0，故③正确；④对称轴为x=﹣＞0，a＜0∴a、b异号，即b＞0，由图知抛物线与y轴交于正半轴，∴c＞0∴abc＜0，故④错误；∴正确结论的序号为②③．故选：B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=﹣判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．3．（2014?南阳二模）二次函数y=ax2+bx+c的图象如图所示，那么关于此二次函数的下列四个结论：①a＜0；②c＞0；③b2﹣4ac＞0；④＜0中，正确的结论有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专数形结合．题：分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵图象开口向下，∴a＜0；故本选项正确；②∵该二次函数的图象与y轴交于正半轴，∴c＞0；故本选项正确；③∵二次函数y=ax2+bx+c的图象与x轴有两个不相同交点，∴根的判别式△=b2﹣4ac＞0；故本选项正确；④∵对称轴x=﹣＞0，∴＜0；故本选项正确；综上所述，正确的结论有4个．故选D．点评：本题主要考查了二次函数的图象和性质，解答本题关键是掌握二次函数y=ax2+bx+c系数符号的确定，做题时要注意数形结合思想的运用，同学们加强训练即可掌握，属于基础题．4．（2014?襄城区模拟）函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．分析：由函数y=x2+bx+c与x轴无交点，可得b2﹣4c＜0；当x=﹣1时，y=1﹣b+c＞0；当x=3时，y=9+3b+c=3；当1＜x＜3时，二次函数值小于一次函数值，可得x2+bx+c＜x，继而可求得答案．解答：解：∵函数y=x2+bx+c与x轴无交点，∴b2﹣4ac＜0；故①正确；当x=﹣1时，y=1﹣b+c＞0，故②错误；∵当x=3时，y=9+3b+c=3，∴3b+c+6=0；③正确；∵当1＜x＜3时，二次函数值小于一次函数值，∴x2+bx+c＜x，∴x2+（b﹣1）x+c＜0．故④正确．故选C．点评：主要考查图象与二次函数系数之间的关系．此题难度适中，注意掌握数形结合思想的应用．5．（2014?宜城市模拟）如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）A．①②B．②③C．②③④D．①②④考点：二次函数图象与系数的关系．分析：根据抛物线开口方向得到a＞0，根据抛物线的对称轴得b=2a＞0，则2a﹣b=0，则可对②进行判断；根据抛物线与y轴的交点在x轴下方得到c＜0，则abc＜0，于是可对①进行判断；由于x=﹣2时，y＜0，则得到4a﹣2b+c ＜0，则可对③进行判断；通过点（﹣5，y1）和点（2，y2）离对称轴的远近对④进行判断．解答：解：∵抛物线开口向上，∴a＞0，∵抛物线对称轴为直线x=﹣=﹣1，∴b=2a＞0，则2a﹣b=0，所以②正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，∴abc＜0，所以①正确；∵x=2时，y＞0，∴4a+2b+c＞0，所以③错误；∵点（﹣5，y1）离对称轴要比点（2，y2）离对称轴要远，∴y1＞y2，所以④正确．故选D．点评：本题考查了二次函数图象与系数的关系：二次函数y=ax2+bx+c（a≠0），二次项系数a决定抛物线的开口方向和大小，当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）．抛物线与y轴交于（0，c）．抛物线与x轴交点个数：△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．6．（2014?莆田质检）如图，二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，对称轴在y轴的右侧，则m的取值范围是（）A．m＞2 B．m＜3 C．m＞3 D．2＜m＜3考点：二次函数图象与系数的关系．分析：由于二次函数的对称轴在y轴右侧，根据对称轴的公式即可得到关于m的不等式，由图象交y轴于负半轴也可得到关于m的不等式，再求两个不等式的公共部分即可得解．解答：解：∵二次函数y=x2+（2﹣m）x+m﹣3的图象交y轴于负半轴，∴m﹣3＜0，解得m＜3，∵对称轴在y轴的右侧，∴x=，解得m＞2，∴2＜m＜3．故选：D．点评：此题主要考查了二次函数的性质，解题的关键是利用对称轴的公式以及图象与y轴的交点解决问题．7．（2014?玉林一模）如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．其中正确结论的个数是（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：∵抛物线的开口方向向下，∴a＜0；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即b2＞4ac，①正确；由图象可知：对称轴x==﹣1，∴2a=b，2a+b=4a，∵a≠0，∴2a+b≠0，②错误；∵图象过点A（﹣3，0），∴9a﹣3b+c=0，2a=b，所以9a﹣6a+c=0，c=﹣3a，③正确；∵抛物线与y轴的交点在y轴的正半轴上，∴c＞0由图象可知：当x=1时y=0，∴a+b+c=0，④正确．故选C．点评：考查了二次函数图象与系数的关系，解答本题关键是掌握二次函数y=ax2+bx+c（a≠0）系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．8．（2014?乐山市中区模拟）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），顶点坐标为（1，n），与y轴的交点在（0，2）、（0，3）之间（包含端点）．有下列结论：①当x＞3时，y＜0；②3a+b＞0；③﹣1≤a≤﹣；④≤n≤4．其中正确的是（）A．①②B．③④C．①③D．①③④考点：二次函数图象与系数的关系．分析：①由抛物线的对称轴为直线x=1，一个交点A（﹣1，0），得到另一个交点坐标，利用图象即可对于选项①作出判断；②根据抛物线开口方向判定a的符号，由对称轴方程求得b与a的关系是b=﹣2a，将其代入（3a+b），并判定其符号；③根据两根之积=﹣3，得到a=，然后根据c的取值范围利用不等式的性质来求a的取值范围；④把顶点坐标代入函数解析式得到n=a+b+c=c，利用c的取值范围可以求得n的取值范围．解答：解：①∵抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），对称轴直线是x=1，∴该抛物线与x轴的另一个交点的坐标是（3，0），∴根据图示知，当x＞3时，y＜0．故①正确；②根据图示知，抛物线开口方向向下，则a＜0．∵对称轴x==1，∴b=﹣2a，∴3a+b=3a﹣2a=a＜0，即3a+b＜0．故②错误；③∵抛物线与x轴的两个交点坐标分别是（﹣1，0），（3，0），∴﹣1×3=﹣3，=﹣3，则a=．∵抛物线与y轴的交点在（0，2）、（0，3）之间（包含端点），∴2≤c≤3，∴﹣1≤≤，即﹣1≤a≤．故③正确；④根据题意知，a=，=1，∴b=﹣2a=，∴n=a+b+c=c．∵2≤c≤3，≤≤4，≤n≤4．故④正确．综上所述，正确的说法有①③④．故选D．点评：本题考查了二次函数图象与系数的关系．二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点抛物线与x轴交点的个数确定．9．（2014?齐齐哈尔二模）已知二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，下列结论正确的个数为（）①b＜0；②c＜0；③a+c＜0；④4a﹣2b+c＞0．A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），（x1，0），且1＜x1＜2，∴对称轴在y轴的右侧，即：﹣＞0，∵a＞0∴b＜0，故①正确；②显然函数图象与y轴交于负半轴，∴c＜0正确；③∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），∴a﹣b+c=0，即a+c=b，∵b＜0，∴a+c＜0正确；④∵二次函数y=ax2+bx+c（a＞0）的图象与x轴交于点（﹣1，0），且a＞0，∴当x=﹣2时，y=4a﹣2b+c＞0，故④正确，故选D．点评：主要考查图象与二次函数系数之间的关系，会利用对称轴的范围求2a与b的关系，以及二次函数与方程之间的转换，根的判别式的熟练运用．。

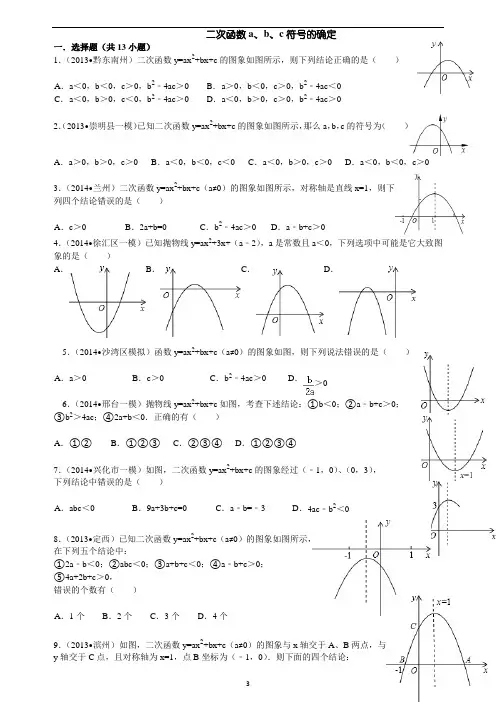
二次函数a、b、c符号的确定一．选择题（共13小题）1．（2013•黔东南州）二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（）A．a＜0，b＜0，c＞0，b2﹣4ac＞0 B．a＞0，b＜0，c＞0，b2﹣4ac＜0C．a＜0，b＞0，c＜0，b2﹣4ac＞0 D．a＜0，b＞0，c＞0，b2﹣4ac＞02．（2013•崇明县一模）已知二次函数y=ax2+bx+c的图象如图所示，那么a，b，c的符号为（）A．a＞0，b＞0，c＞0 B．a＜0，b＜0，c＜0 C．a＜0，b＞0，c＞0 D．a＜0，b＜0，c＞03．（2014•兰州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）A．c＞0 B．2a+b=0 C．b2﹣4ac＞0 D．a﹣b+c＞04．（2014•徐汇区一模）已知抛物线y=ax2+3x+（a﹣2），a是常数且a＜0，下列选项中可能是它大致图象的是（）A．B．C ．D．5．（2014•沙湾区模拟）函数y=ax2+bx+c（a≠0）的图象如图，则下列说法错误的是（）A．a＞0 B．c＞0 C．b2﹣4ac＞0 D．＞06．（2014•邢台一模）抛物线y=ax2+bx+c如图，考查下述结论：①b＜0；②a﹣b+c＞0；③b2＞4ac；④2a+b＜0．正确的有（）A．①②B．①②③C．②③④D．①②③④7．（2014•兴化市一模）如图，二次函数y=ax2+bx+c的图象经过（﹣1，0）、（0，3），下列结论中错误的是（）A．a bc＜0 B．9a+3b+c=0 C．a﹣b=﹣3 D．4ac﹣b2＜08．（2013•定西）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0，错误的个数有（）A．1个B．2个C．3个D．4个9．（2013•滨州）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴为x=1，点B坐标为（﹣1，0）．则下面的四个结论：①2a+b=0；②4a﹣2b+c＜0；③ac＞0；④当y＜0时，x＜﹣1或x＞2．其中正确的个数是（）A．1B．2C．3D．410．（2013•邢台一模）已知二次函数y=ax2+bx+c的图象如图所示，则下列条件正确的是（）A．a c＜0 B．b2﹣4ac＜0 C．b＞0 D． a＞0、b＜0、c＞011．（2013•红桥区一模）如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①abc＞0；②4a﹣2b+c＜0；③2a﹣b＜0；④b2+8a＞4ac．其中正确的有（）A．1个B．2个C．3个D．4个12．（2013•百色）在反比例函数y=中，当x＞0时，y随x的增大而增大，则二次函数y=mx2+mx的图象大致是图中的（）A．B．C．D．13．（2013•长安区模拟）二次函数y=ax2+bx+c的图象如图所示，下列结论：①a+b+c＞0；②a﹣b+c＞0；③abc=0；④2a﹣b=0，其中正确的有（）A．1个B．2个C．3个D．4个二．解答题（共2小题）14．（2008•密云县一模）已知抛物线y=ax2+bx+c的一段图象如图所示．（1）确定a、b、c的符号；（2）求a+b+c的取值范围．15．已知抛物线y=ax2+bx+c的图象如图所示，（1）判断a，b，c及b2﹣4ac，a﹣b+c的符号；（2）求a+b+c的值；（3）下列结论：①b＜1，②b＜2a，③a＞，④a+c＜1，⑤﹣a﹣b+c＜0．其中正确的有_________，请说明理由．参考答案与试题解析一．选择题（共13小题）1．（2013•黔东南州）二次函数y=ax2+bx+c的图象如图所示，则下列结论正确的是（）A．a＜0，b＜0，c＞0，b2﹣4ac＞0 B．a＞0，b＜0，c＞0，b2﹣4ac＜0C．a＜0，b＞0，c＜0，b2﹣4ac＞0 D．a＜0，b＞0，c＞0，b2﹣4ac＞0考点：二次函数图象与系数的关系．专题：压轴题．分析：由抛物线的开口方向判断a与0的关系，再结合抛物线的对称轴与y轴的关系判断b与0的关系，由抛物线与y轴的交点判断c与0的关系，根据抛物线与x轴交点的个数判断b2﹣4ac与0的关系．解答：解：∵抛物线的开口向下，∴a＜0，∵对称轴在y轴右边，∴a，b异号即b＞0，∵抛物线与y轴的交点在正半轴，∴c＞0，∵抛物线与x轴有2个交点，∴b2﹣4ac＞0．故选D．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0．（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号．（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0．（4）b2﹣4ac由抛物线与x轴交点的个数确定：2个交点，b2﹣4ac＞0；1个交点，b2﹣4ac=0；没有交点，b2﹣4ac＜0．2．（2013•崇明县一模）已知二次函数y=ax2+bx+c的图象如图所示，那么a，b，c的符号为（）A．a＞0，b＞0，c＞0 B．a＜0，b＜0，c＜0 C．a＜0，b＞0，c＞0 D．a＜0，b＜0，c＞0考点：二次函数图象与系数的关系．专题：推理填空题．分析：根据二次函数图象开口向下确定出a为负数，根据对称轴结合a为负数确定出b的正负情况，根据二次函数图象与y轴的交点即可确定出c的正负情况，从而最后得解．解答：解：∵二次函数图象开口向下，∴a＜0，∵对称轴x=﹣＜0，∴b＜0，∵二次函数图象与y轴的正半轴相交，∴c＞0，∴a＜0，b＜0，c＞0．故选D．点评：本题考查了二次函数图象与系数的关系，熟练掌握二次函数图象的开口方向、对称轴、与y轴的交点与系数的关系是解题的关键．3．（2014•兰州）二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是直线x=1，则下列四个结论错误的是（）A．c＞0 B．2a+b=0 C．b2﹣4ac＞0 D．a﹣b+c＞0考点：二次函数图象与系数的关系．专题：数形结合．分析：本题考查二次函数图象的相关知识与函数系数的联系．需要根据图形，逐一判断．解答：解：A、因为二次函数的图象与y轴的交点在y轴的上方，所以c＞0，正确；B、由已知抛物线对称轴是直线x=﹣=1，得2a+b=0，正确；C、由图知二次函数图象与x轴有两个交点，故有b2﹣4ac＞0，正确；D、直线x=﹣1与抛物线交于x轴的下方，即当x=﹣1时，y ＜0，即y=ax 2+bx+c=a﹣b+c＜0，错误．故选：D．点评：在解题时要注意二次函数的系数与其图象的形状，对称轴，特殊点的关系，也要掌握在图象上表示一元二次方程ax2+bx+c=0的解的方法．同时注意特殊点的运用．4．（2014•徐汇区一模）已知抛物线y=ax2+3x+（a﹣2），a是常数且a＜0，下列选项中可能是它大致图象的是（）A．B．C．D．考点：二次函数图象与系数的关系．分析：根据抛物线对称轴位置和a，b的关系以及利用图象开口方向与a的关系，得出图象开口向下，对称轴经过x轴正半轴，利用图象与y轴交点和c的符号，进而得出答案．解答：解：∵抛物线y=ax2+3x+（a﹣2），a是常数且a＜0，∴图象开口向下，a﹣2＜0，∴图象与y轴交于负半轴，∵a＜0，b=3，∴抛物线对称轴在y轴右侧．故选：B．点评：此题主要考查了二次函数图象与系数的关系，正确把握图象对称轴位置与a，b的关系是解题关键．5．（2014•沙湾区模拟）函数y=ax2+bx+c（a≠0）的图象如图，则下列说法错误的是（）A．a＞0 B．c＞0 C．b2﹣4ac＞0 D．＞0考点：二次函数图象与系数的关系．分析：由抛物线开口向上得到a＞0，由抛物线与y轴的交点在x轴上方得c＞0，图象与x轴有两个交点得b2﹣4ac＞0，对称轴在y轴右侧得，则，据此逐一判断即可．解答：解：：A、∵抛物线开口向上，∴a＞0，所以A选项的说法正确；B、∵抛物线与y轴的交点在x轴上方，∴c＞0，所以B选项的说法正确；C、∵抛物线与x轴有两交点，∴b2﹣4ac＞0，y＜0，∴4a+2b+c＜0，所以C选项的说法正确；D、∵对称轴在y轴右侧得，∴，所以D选项的说法错误．故选：D．点评：本题考查了二次函数的图象与系数的关系：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，当a ＞0，抛物线开口向上；对称轴为直线x=﹣；抛物线与y轴的交点坐标为（0，c）；当b2﹣4ac ＞0，抛物线与x轴有两个交点；当b2﹣4ac=0，抛物线与x轴有一个交点；当b2﹣4ac＜0，抛物线与x轴没有交点．6．（2014•邢台一模）抛物线y=ax2+bx+c如图，考查下述结论：①b＜0；②a﹣b+c＞0；③b2＞4ac；④2a+b＜0．正确的有（）A．①②B．①②③C．②③④D．①②③④考点：二次函数图象与系数的关系．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①图象开口向上，与y轴交于负半轴，对称轴在y轴右侧，能得到：a＞0，c＜0，﹣＞0，b＜0，正确；②由图象知当x=﹣1时，y=a﹣b+c＞0，正确；③图象与x轴有两个交点，所以b2﹣4ac＞0，即b2＞4ac正确；④由图象知，即2a+b=0，本项错误．故选B．点评：二次函数y=ax2+bx+c系数符号的确定：（1）a由抛物线开口方向确定：开口方向向上，则a＞0；否则a＜0；（2）b由对称轴和a的符号确定：由对称轴公式x=判断符号；（3）c由抛物线与y轴的交点确定：交点在y轴正半轴，则c＞0；否则c＜0；（4）b2﹣4ac由抛物线与x轴交点的个数确定：①2个交点，b2﹣4ac＞0；②1个交点，b2﹣4ac=0；③没有交点，b2﹣4ac＜0．（5）当x=1时，可以确定y=a+b+c的值；当x=﹣1时，可以确定y=a﹣b+c的值．7．（2014•兴化市一模）如图，二次函数y=ax2+bx+c的图象经过（﹣1，0）、（0，3），下列结论中错误的是（）A．a bc＜0 B．9a+3b+c=0 C．a﹣b=﹣3 D．4ac﹣b2＜0考点：二次函数图象与系数的关系．分析：A、由对称轴可判断ab的符号，再由抛物线与y轴的交点可判断c的符号，从而确定abc的符号；B、观察图象，不能得出x=3时，函数值的符号，所以9a+3b+c不一定等于0；C、将（﹣1，0）、（0，3）分别代入y=ax2+bx+c，即可得出a﹣b=﹣3；D、根据抛物线与x轴的交点个数可判断b2﹣4ac的符号，从而确定4ac﹣b2的符号．解答：解：A、∵抛物线对称轴x=﹣＞0，∴ab＜0，又∵抛物线与y轴交于正半轴，∴c＞0，∴abc＜0，正确，故本选项不符合题意；B、观察图象，由于没有给出对称轴方程，所以不能得出x=3时，函数值的符号，所以9a+3b+c不一定等于0，即9a+3b+c=0不一定正确，故本选项符合题意；C、∵二次函数y=ax2+bx+c的图象经过（﹣1，0）、（0，3），∴，②代入①，整理，得a﹣b=﹣3，正确，故本选项不符合题意；D、∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，即4ac﹣b2＜0，正确，故本选项不符合题意．故选B．点评：本题考查了二次函数y=ax2+bx+c的图象与系数的关系：当a＜0，抛物线开口向下；抛物线的对称轴为直线x=﹣；抛物线与y轴的交点坐标为（0，c）；当b2﹣4ac＞0，抛物线与x轴有两个交点．8．（2013•定西）已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，在下列五个结论中：①2a﹣b＜0；②abc＜0；③a+b+c＜0；④a﹣b+c＞0；⑤4a+2b+c＞0，错误的个数有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：压轴题．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，利用图象将x=1，﹣1，2代入函数解析式判断y的值，进而对所得结论进行判断．解答：解：①∵由函数图象开口向下可知，a＜0，由函数的对称轴x=﹣＞﹣1，故＜1，∵a＜0，∴b＞2a，所以2a﹣b＜0，①正确；②∵a＜0，对称轴在y轴左侧，a，b同号，图象与y轴交于负半轴，则c＜0，故abc＜0；②正确；③当x=1时，y=a+b+c＜0，③正确；④当x=﹣1时，y=a﹣b+c＜0，④错误；⑤当x=2时，y=4a+2b+c＜0，⑤错误；故错误的有2个．故选：B．点评：此题主要考查了图象与二次函数系数之间的关系，将x=1，﹣1，2代入函数解析式判断y的值是解题关键．9．（2013•滨州）如图，二次函数y=ax2+bx+c（a≠0）的图象与x轴交于A、B两点，与y轴交于C点，且对称轴为x=1，点B坐标为（﹣1，0）．则下面的四个结论：①2a+b=0；②4a﹣2b+c＜0；③ac＞0；④当y＜0时，x＜﹣1或x＞2．其中正确的个数是（）A．1B．2C．3D．4考点：二次函数图象与系数的关系．专题：压轴题．分析：根据对称轴为x=1可判断出2a+b=0正确，当x=﹣2时，4a﹣2b+c＜0，根据开口方向，以及与y轴交点可得ac＜0，再求出A点坐标，可得当y＜0时，x＜﹣1或x＞3．解答：解：∵对称轴为x=1，∴x=﹣=1，∴﹣b=2a，∴①2a+b=0，故此选项正确；∵点B坐标为（﹣1，0），∴当x=﹣2时，4a﹣2b+c＜0，故此选项正确；∵图象开口向下，∴a＜0，∵图象与y轴交于正半轴上，∴c＞0，∴ac＜0，故ac＞0错误；∵对称轴为x=1，点B坐标为（﹣1，0），∴A点坐标为：（3，0），∴当y＜0时，x＜﹣1或x＞3．，故④错误；故选：B．点评：此题主要考查了二次函数与图象的关系，关键掌握二次函数y=ax2+bx+c（a≠0）①二次项系数a决定抛物线的开口方向和大小．当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；IaI还可以决定开口大小，IaI越大开口就越小．②一次项系数b和二次项系数a共同决定对称轴的位置．当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）③．常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．④抛物线与x轴交点个数．△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．10．（2013•邢台一模）已知二次函数y=ax2+bx+c的图象如图所示，则下列条件正确的是（）A．a c＜0 B．b2﹣4ac＜0 C．b＞0 D．a＞0、b＜0、c＞0考点：二次函数图象与系数的关系．分析：由函数图象可得：a＞0，b＜0，c＞0，再结合图象判断各选项．解答：解：由函数图象可得：a＞0，b＜0，c＞0，A、ac＜0，错误；B、b2﹣4ac＜0，错误；C、b＞0，错误；D、a＞0、b＜0、c＞0，正确．故选D．点评：本题考查了二次函数图象与系数的关系，重点是从函数图象上得到重要的信息．11．（2013•红桥区一模）如图所示，二次函数y=ax2+bx+c（a≠0）的图象经过点（﹣1，2），且与x轴交点的横坐标分别为x1，x2，其中﹣2＜x1＜﹣1，0＜x2＜1，下列结论：①abc＞0；②4a﹣2b+c＜0；③2a﹣b＜0；④b2+8a＞4ac．其中正确的有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系；抛物线与x轴的交点．分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．解答：解：①∵该函数图象的开口向下，∴a＜0；又对称轴x=﹣＜0，∴b＜0；而该函数图象与y轴交于正半轴，故c＞0，∴abc＞0，正确；②当x=﹣2时，y＜0，即4a﹣2b+c＜0；正确；③根据题意得，对称轴﹣1＜x=﹣＜0，∴2a﹣b＜0，正确；④∵＞2，a＜0，∴4ac﹣b2＜8a，即b2+8a＞4ac，正确．故选D．点评：本题考查二次函数y=ax2+bx+c系数符号的确定由抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数确定．12．（2013•百色）在反比例函数y=中，当x＞0时，y随x的增大而增大，则二次函数y=mx2+mx的图象大致是图中的（）A．B．C．D．考点：二次函数图象与系数的关系；反比例函数的性质．分析：根据反比例函数图象的性质确定出m＜0，则二次函数y=mx2+mx 的图象开口方向向下，且与y 轴交于负半轴，即可得出答案．解答：解：∵反比例函数y=，中，当x＞0时，y随x的增大而增大，∴根据反比例函数的性质可得m＜0；该反比例函数图象经过第二、四象限，∴二次函数y=mx2+mx的图象开口方向向下，且与y轴交于负半轴．∴只有A选项符合．故选A．点评：本题考查了二次函数图象、反比例函数图象．利用反比例函数的性质，推知m＜0是解题的关键，体现了数形结合的思想．13．（2013•长安区模拟）二次函数y=ax2+bx+c的图象如图所示，下列结论：①a+b+c＞0；②a﹣b+c＞0；③abc=0；④2a﹣b=0，其中正确的有（）A．1个B．2个C．3个D．4个考点：二次函数图象与系数的关系．专题：数形结合．分析：观察函数图象得到x=1时，y＜0；x=﹣1时，y＞0，所以a+b+c＜0，a﹣b+c＞0，则可对①②进行判断；由于抛物线过原点，所以c=0，可对③进行判断；根据抛物线的对称轴为直线x=﹣1，即x=﹣=﹣1，则可对④进行判断．解答：解：∵x=1时，y＜0，∴a+b+c＜0；所以①错误；∵x=﹣1时，y＞0，∴a﹣b+c＞0；所以②正确；∵抛物线过原点，∴c=0，∴abc=0，所以③正确；∵抛物线的对称轴为直线x=﹣1，∴x=﹣=﹣1，∴2a﹣b=0，所以④正确．故选C．点评：本题考查了二次函数的图象与系数的关系：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，当a＞0，抛物线开口向上；对称轴为直线x=﹣；抛物线与y轴的交点坐标为（0，c）；当b2﹣4ac＞0，抛物线与x轴有两个交点；当b2﹣4ac=0，抛物线与x轴有一个交点；当b2﹣4ac＜0，抛物线与x轴没有交点．二．解答题（共2小题）14．（2008•密云县一模）已知抛物线y=ax2+bx+c的一段图象如图所示．（1）确定a、b、c的符号；（2）求a+b+c的取值范围．考点：二次函数图象与系数的关系．专题：计算题．分析：（1）根据抛物线开口向上，则a＞0，对称轴在x轴正半轴可知﹣＞0，与y轴交点在y轴负半轴可知c＜0；（2）再根据抛物线y=ax2+bx+c过点（﹣1，0），（0，﹣1），即可求出a+b+c的取值范围．解答：解：（1）根据抛物线开口向上，则a＞0，∵对称轴在x轴正半轴可知﹣＞0，∴b＜0，又与y轴交点在y轴负半轴，∴c＜0，故a＞0，b＜0，c＜0；（2）∵抛物线y=ax2+bx+c过点（﹣1，0），（0，﹣1），∴a﹣b+c=0，c=﹣1，即a﹣b=1，a=b+1，∴a+b+c=b+1+b﹣1=2b，∵b＜0，∴2b＜0，∵a＞0，∴b+1＞0，∴b＞﹣1，2b＞﹣2，故，﹣2＜a+b+c＜0．点评：本题考查了二次函数图象与系数的关系，难度一般，关键是正确获取图象信息进行解题．15．已知抛物线y=ax2+bx+c的图象如图所示，（1）判断a，b，c及b2﹣4ac，a﹣b+c的符号；（2）求a+b+c的值；（3）下列结论：①b＜1，②b＜2a，③a＞，④a+c＜1，⑤﹣a﹣b+c＜0．其中正确的有①③④⑤，请说明理由．考点：二次函数图象与系数的关系．分析：（1）根据抛物线的开口向上确定a是正数，对称轴在y轴右侧，确定b＜0；再根据抛物线y轴的负半轴相交确定c是负数，根据抛物线与x轴交于两点，确定b2﹣4ac＞0，根据图象可知x=﹣1时，y＜0，确定＜0；（2）由函数的图象可知当x=1时，y=﹣3，即可得出a+b+c=﹣3；（3）由对称轴x=﹣=得出b=﹣a＜0，即可判定①的结论；由﹣=＜1，＞1，得出b ＞2a即可判定②的结论；由x1=﹣1.5，x2=2.5，所以=﹣，因为c=﹣3，a=＞，即可判定③的结论；由a=，c=﹣3，得出a+c=﹣＜1，即可判定④结论；由b=﹣a，得出﹣a﹣b+c=c=﹣3，即可判定⑤的结论．解答：解：（1）∵抛物线开口向上，∴a＞0，∵对称轴在y轴右侧，∴b＜0；∵抛物线与y轴负半轴相交，∴c＜0，∵抛物线与x轴交于两点，∴b2﹣4ac＞0，∵x=﹣1时，y＜0，∴a﹣b+c＜0；（2）由函数的图象可知当x=1时，y=﹣3，所以a+b+c=﹣3；（3）∵对称轴x=﹣=∴b=﹣a＜0∴b＜1；故①正确；∵﹣=＜1，∴＞1，∵a＞0，∴b＞2a故②错误；∵x1=﹣1.5，x2=2.5，∴=﹣，∵c=﹣3，∴a=＞，故③正确；∵a=，c=﹣3，∴a+c=﹣＜1，故④正确；∵b=﹣a，∴﹣a﹣b+c=c=﹣3＜0，故⑤正确．故答案为：①③④⑤．点评：本题考查了二次函数的图象与系数的关系：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，当a ＞0，抛物线开口向上；对称轴为直线x=﹣；抛物线与y轴的交点坐标为（0，c）；当b2﹣4ac ＞0时，抛物线与x轴有两个交点．。

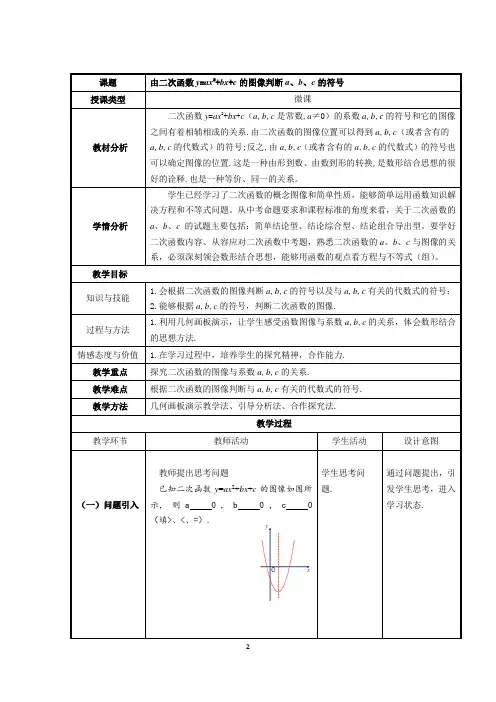
课题由二次函数y=ax2+bx+c的图像判断a、b、c的符号授课类型微课教材分析二次函数y=ax2+bx+c（a,b,c是常数,a≠0）的系数a,b,c的符号和它的图像之间有着相辅相成的关系.由二次函数的图像位置可以得到a,b,c（或者含有的a,b,c的代数式）的符号;反之,由a,b,c（或者含有的a,b,c的代数式）的符号也可以确定图像的位置.这是一种由形到数、由数到形的转换,是数形结合思想的很好的诠释.也是一种等价、同一的关系。

学情分析学生已经学习了二次函数的概念图像和简单性质，能够简单运用函数知识解决方程和不等式问题。

从中考命题要求和课程标准的角度来看，关于二次函数的a、b、c的试题主要包括：简单结论型、结论综合型、结论组合导出型。

要学好二次函数内容、从容应对二次函数中考题，熟悉二次函数的a、b、c与图像的关系，必须深刻领会数形结合思想，能够用函数的观点看方程与不等式（组）。

教学目标知识与技能1.会根据二次函数的图像判断a,b,c的符号以及与a,b,c有关的代数式的符号；2.能够根据a,b,c的符号，判断二次函数的图像.过程与方法1.利用几何画板演示，让学生感受函数图像与系数a,b,c的关系，体会数形结合的思想方法.情感态度与价值 1.在学习过程中，培养学生的探究精神，合作能力.教学重点探究二次函数的图像与系数a,b,c的关系.教学难点根据二次函数的图像判断与a,b,c有关的代数式的符号.教学方法几何画板演示教学法、引导分析法、合作探究法.教学过程教学环节教师活动学生活动设计意图（一）问题引入教师提出思考问题已知二次函数y=ax2+bx+c的图像如图所示，则a 0 ， b 0 ， c 0（填>、<、=）.学生思考问题.通过问题提出，引发学生思考，进入学习状态.。

二次函数a、b、c、△符号问题及相关问题一选择题1.如图所示，抛物线的图象则下列结论正确的是（）A a<0，b<0，c＞0，b2＜4acB a<0，b>0，c<0，b2＜4acC a<0，b>0，c＞0，b2>4acD a>0，b<0，c＞0，b2>4ac2.如图a＜0，c＞0那么y＝ax2＋bx＋c的图象是（）3.已知二次函数y=ax2+bx+c (a≠0）的图象如图所示，则下列结论：①a、b同号；②当x=1和x=3时，函数值相等；③ 4a+b=0；④当y=－2时，x的值只能取0．其中正确的个数是（）A l个 B 2个 C 3个 D 4个4.二次函数y=mx2+2mx-（3-m）的图象如图所示，则m的取值范围是（）A m＜3B m＞3C m＞0D 0＜m＜35.在同一直角坐标系中，一次函数y=ax+c和二次函数y=ax2+c的图象大致为( )6.已知抛物线y=x2+bx+c的部分图象如右图所示，若y<0，则x的取值范围是（）A −1<x<4B -1<x<3C x<-1或x>4D x<-1或x>37.在某次投篮中，球的运动路线是y=-0.2x2+3.5的一部分(如图)，若命中篮圈中心，则他与篮底的距离为( )A 3.5mB 4mC 4.5mD 4.6m8.若抛物线y=x2+8x+h2的顶点在x轴上，则（）A h=0 B h=±16 C h=±4 D h=49.如果二次函数y=ax2+m的值恒大于0，那么必有（）A a＞0，m取任意实数B a＞0，m＞0C a＜0，m＞0D a，m均可取任意实数10.已知a-b+c=0，9a+3b+c=0，则抛物线y=ax2+bx+c的顶点可能在( )A 第一或二象限B 第三或四象限C 第一或四象限D 第二或四象限11.抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），且满足4a+2b+c＞0，以下结论：①a+b＞0；②a+c＞0；③﹣a+b+c ＞0；④b2﹣2ac＞5a2，其中正确的个数有（）A．1个B．2个C．3个D．4个12.物线y=ax2+bx+c(a≠0)全部图象都在x轴下方，则( )A a>0，b2-4ac≥0B a>0，b2-4ac<0C a>0，b2-4ac≥0D a<0，b2-4ac<0二填空题13.若二次函数y=(a-1)x2-2x+1的图象与x轴只有一个交点，则a=________14.不论x取什么实数，y=2x2-6x+m的图象都在x轴的上方，那么m的取值范围是________；y=mx2－3x＋2m－m2的图象经过原点，则m＝15.二次函数y＝x2-(m-4)x+9的图象的顶点在y轴上，则m＝16.二次函数y＝x2＋2kx＋8的顶点在x轴上，则k＝17.已知抛物线y＝x2－2（k+1）x＋16的顶点在x轴上，则k的值为______18.抛物线y＝x2－(m－4)x－m与x轴的两个交点关于y轴对称，其顶点坐标为______19.已知抛物线y＝x2+2（m－3）x＋1的顶点在x轴上，则m＝______顶点坐标是_________20.平移抛物线y = x2+2x-8，使它经过原点，写出平移后抛物线的一个解析式21.如果二次函数y=x2-3x-2k,不论x取任何实数,都有y>0,则k的取值范围是________22.把抛物线y=2(x+1)2向下平移______单位后,所得抛物线在x轴上截得的线段长为523.抛物线y=-3(x+2)2的顶点坐标是_____________,若将它旋转180后得新的抛物线,其解析式为____________________24.把y=x2+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x2-3x+5,则有b=_____，c=_____三解答题25.如图，抛物线y＝ax2+bx＋c确定a，b，c，b2-4ac，a+b+c，a-b+c的符号26.抛物线y＝ax2+bx＋c的图像如图，对称轴是直线x＝－1确定a,b,c，Δ及a－b＋c 的符号27.已知抛物线y＝ax2+bx+c的一段图象如图所示．（1）确定a、b、c的符号；（2）求a+b+c的取值范围．28.如图为二次函数y=ax2＋bx＋c的图象，在下列说法中：①ac＜0；②方程ax2＋bx＋c=0的根是x1= －1, x2= 3；③a＋b＋c＞0；④当x＞1时，y随x的增大而增大.正确的说法有_____________29.有一个抛物线形的桥洞，桥洞离水面的最大高度BM为3米，跨度OA为6米，以OA所在直线为x轴，O为原点建立直角坐标系（如图所示）．（1）请你直接写出O、A、M三点的坐标；（2）一艘小船平放着一些长3米，宽2米且厚度均匀的矩形木板，要使该小船能通过此桥洞，问这些木板最高可堆放多少米（设船身底板与水面在同一平面）？30.如图，二次函数y=x2+bx+c的图象经过点M（1，—2）、N（—1，6）.（1）求二次函数的关系式；（2）把Rt△ABC 放在坐标系内，其中∠CAB=900，点A、B的坐标分别为（1，0）、（4，0），BC = 5，将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离.二次函数a、b、c、△符号问题及相关问题答案1.C2.D3.B4.D5.B6.B7.B8.C9.B 10.C 11.D 12.D11.分析（1）因为抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），把点（﹣1，0）代入解析式，结合4a+2b+c＞0，即可整理出a+b＞0；（2）②+①×2得，6a+3c＞0，结合a＜0，故可求出a+c＞0；（3）画草图可知c＞0，结合a﹣b+c ＝0，可整理得﹣a+b+c＝2c＞0，从而求得﹣a+b+c＞0；（4）把（﹣1，0）代入解析式得a﹣b+c＝0，可得出2a+c＞0，再由a＜0，可知c＞0则c﹣2a＞0，故可得出（c+2a）（c﹣2a）＞0，即b2﹣2ac﹣5a2＞0，进而可得出结论．解：（1）因为抛物线y＝ax2+bx+c（a＜0）经过点（﹣1，0），所以原式可化为a﹣b+c＝0 ①，又因为4a+2b+c＞0 ②，所以②﹣①得：3a+3b＞0，即a+b＞0；（2）②+①×2得，6a+3c＞0，即2a+c＞0，∴a+c＞﹣a，∵a＜0，∴﹣a＞0，故a+c＞0；（3）因为4a+2b+c＞0，可以看作y＝ax2+bx+c（a＜0）当x＝2时的值大于0，草图为：可见c＞0，∵a﹣b+c＝0，∴﹣a+b﹣c＝0，两边同时加2c得﹣a+b﹣c+2c＝2c，整理得﹣a+b+c＝2c＞0，即﹣a+b+c＞0；（4）∵过（﹣1，0），代入得a﹣b+c＝0∴b2﹣2ac﹣5a2＝（a+c）2﹣2ac﹣5a2＝c2﹣4a2＝（c+2a）（c﹣2a）又∵4a+2b+c＞04a+2（a+c）+c＞0，即2a+c＞0①，∵a＜0，∴c＞0则c﹣2a＞0②，由①②知（c+2a）（c﹣2a）＞0，所以b2﹣2ac﹣5a2＞0，即b2﹣2ac＞5a2,综上可知正确的个数有4个．故选：D．13.2 14.m＞9／2，2 15.4 16.±22 17.3或-5 18.（0，-4） 19.4或2，（1,0）或（-1,0） 20.y=x2+2x 21.k＜-9／8 22. 25／2 23.（-2,0），y=3（x+2）2 24.3，725. a＜0，b＞0，c＞0，b2-4ac＞0，a+b+c＞0，a-b+c＜026.a＜0，b＜0，c＞0，△＞0，a-b+c＞027.解：（1）根据抛物线开口向上，则a＞0，∵对称轴在x轴正半轴可知﹣＞0，∴b＜0，又与y轴交点在y轴负半轴，∴c＜0，故a＞0，b＜0，c＜0；（2）∵抛物线y＝ax2+bx+c过点（﹣1，0），（0，﹣1），∴a﹣b+c＝0，c＝﹣1，即a﹣b＝1，a＝b+1，∴a+b+c＝b+1+b﹣1＝2b，∵b＜0，∴2b＜0，∵a＞0，∴b+1＞0，∴b＞﹣1，2b＞﹣2，故，﹣2＜a+b+c＜0．28.①②④29.解：（1）解：如图，O（0，0）．∵OA为6米，∴A（6，0），又∵BM的对称轴，BM为3米，∴M（3，3）．综上所述，O（0，0），A（6，0），M（3，3）．（2）设抛物线的关系式为y＝a（x﹣3）2+3，因为抛物线过点（0，0），所以0＝a（0﹣3）2+3，解得a＝﹣，所以y＝﹣（x﹣3）2+3＝﹣x2+2x，要使木板堆放最高，依据题意，得B点应是木板宽CD的中点，把x＝2代入y＝﹣x2+2x，得y＝，所以这些木板最高可堆放米．30.解：（1）∵M（1，﹣2），N（﹣1，6）在二次函数y＝x2+bx+c的图象上，∴，解得二次函数的关系式为y＝x2﹣4x+1．（2）Rt△ABC中，AB＝3，BC，＝5，∴AC＝4，4＝x2﹣4x+1，x2﹣4x﹣3＝0，解得（负值不合题意舍去），∵A（1，0），∴点C落在抛物线上时，△ABC向右平移（1+）个单位．。

二次函数中的abc的含义在二次函数中，abc分别代表着三个不同的参数，即二次项系数（a）、一次项系数（b）和常数项（c）。

这些参数用来描述函数图像的特征，并决定了二次函数的形状，位置和方向。

接下来，我们将详细解释每个参数的含义，并讨论它们对函数图像的影响。

1.二次项系数（a）：二次项系数（a）表示二次函数中二次项的系数。

当a>0时，二次函数的图像开口向上，形状类似于一个U形；当a<0时，二次函数的图像开口向下，形状类似于一个倒U形。

系数a的绝对值越大，图像的开口越窄，曲线越陡峭，而绝对值小的a则代表着开口较宽的曲线。

2.一次项系数（b）：一次项系数（b）表示二次函数中一次项的系数。

一次项决定了二次函数的图像与y轴的交点位置。

当b>0时，二次函数与y轴的交点在y轴上方；当b<0时，二次函数与y轴的交点在y轴下方。

系数b的绝对值越大，图像与y轴之间的距离越远，而绝对值小的b则代表着图像与y轴之间的距离越近。

3.常数项（c）：常数项（c）表示二次函数中的常数。

常数项决定了二次函数与y 轴的截距，即图像与y轴的交点位置。

常数项c的值决定了图像在y 轴上的上下平移。

当c>0时，图像向上平移；当c<0时，图像向下平移。

增加常数项的绝对值将把图像向下移动，而减小常数项的绝对值将使图像向上移动。

综上所述，二次函数中的abcd分别代表二次项系数、一次项系数和常数项。

a决定了图像的形状，b决定了图像与y轴之间的距离和交点的位置，c决定了图像在y轴上的上下平移。

这些参数共同作用，决定了二次函数的图像特征，帮助我们分析和理解二次函数在数学和实际问题中的应用。

二次函数的平移、翻折与旋转以及a、b、c符号问题1、抛物线的一般式与顶点式的互化关系：y＝ax2＋bx＋c————→y＝a(x＋b2a)2＋4ac－b24a2、强调利用抛物线的对称性进行画图，先确定抛物线的顶点、对称轴，利用对称性列表、描点、连线。

3、抛物线的平移抓住关键点顶点的移动；例题：1、（2015•龙岩）抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是．考点：二次函数图象与几何变换．分析：根据旋转的性质，可得a的绝对值不变，根据中心对称，可得答案．解答：解：将y=2x2﹣4x+3化为顶点式，得y=2（x﹣1）2+1，抛物线y=2x2﹣4x+3绕坐标原点旋转180°所得的抛物线的解析式是y=﹣2（x+1）2﹣1，化为一般式，得y=﹣2x2﹣4x﹣3，故答案为：y=﹣2x2﹣4x﹣3．点评：本题考查了二次函数图象与几何变换，利用了中心对称的性质．2、（2015•湖州）如图，已知抛物线C1：y=a1x2+b1x+c1和C2：y=a2x2+b2x+c2都经过原点，顶点分别为A，B，与x轴的另一交点分别为M，N，如果点A与点B，点M与点N都关于原点O成中心对称，则称抛物线C1和C2为姐妹抛物线，请你写出一对姐妹抛物线C1和C2，使四边形ANBM恰好是矩形，你所写的一对抛物线解析式是和．考点：二次函数图象与几何变换．专题：新定义．分析：连接AB，根据姐妹抛物线的二次项的系数互为相反数，一次项系数相等且不等于零，常数项都是零，设抛物线C1的解析式为y=ax2+bx，根据四边形ANBM恰好是矩形可得△AOM是等边三角形，设OM=2，则点A的坐标是（1，），求出抛物线C1的解析式，从而求出抛物线C2的解析式．解答：解：连接AB，根据姐妹抛物线的定义，可得姐妹抛物线的二次项的系数互为相反数，一次项系数相等且不等于零，常数项都是零，设抛物线C1的解析式为y=ax2+bx，根据四边形ANBM恰好是矩形可得：OA=OM，∵OA=MA，∴△AOM是等边三角形，设OM=2，则点A的坐标是（1，），则，解得：则抛物线C1的解析式为y=﹣x2+2x，抛物线C2的解析式为y=x2+2x，故答案为：y=﹣x2+2x，y=x2+2x．w W w .x K b 1.c o M点评：此题考查了二次函数的图象与几何变换，用到的知识点是姐妹抛物线的定义、二次函数的图象与性质、矩形的判定，关键是根据姐妹抛物线的定义得出姐妹抛物线的二次项的系数、一次项系数、常数项之间的关系．3、（2015•绥化）把二次函数y=2x2的图象向左平移1个单位长度，再向下平移2个单位长度，平移后抛物线的解析式为．考点：二次函数图象与几何变换．分析：直接根据“上加下减，左加右减”的原则进行解答．解答：解：由“左加右减”的原则可知，将二次函数y=2x2的图象向左平移1个单位长度所得抛物线的解析式为：y=2（x+1）2，即y=2（x+1）2；由“上加下减”的原则可知，将抛物线y=2（x+1）2向下平移2个单位长度所得抛物线的解析式为：y=2（x+1）2﹣2，即y=2（x+1）2﹣2．故答案为：y=2（x+1）2﹣2．点评：本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．4、（2015•岳阳）如图，已知抛物线y=ax2+bx+c与x轴交于A、B两点，顶点C的纵坐标为﹣2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论正确的是．（写出所有正确结论的序号）①b＞0②a﹣b+c＜0③阴影部分的面积为4④若c=﹣1，则b2=4a．考点：二次函数图象与几何变换；二次函数图象与系数的关系．分析：①首先根据抛物线开口向上，可得a＞0；然后根据对称轴为x=﹣＞0，可得b＜0，据此判断即可．②根据抛物线y=ax2+bx+c的图象，可得x=﹣1时，y＞0，即a﹣b+c＞0，据此判断即可．③首先判断出阴影部分是一个平行四边形，然后根据平行四边形的面积=底×高，求出阴影部分的面积是多少即可．④根据函数的最小值是，判断出c=﹣1时，a、b的关系即可．解答：解：∵抛物线开口向上，∴a＞0，又∵对称轴为x=﹣＞0，∴b＜0，∴结论①不正确；∵x=﹣1时，y＞0，∴a﹣b+c＞0，∴结论②不正确；∵抛物线向右平移了2个单位，∴平行四边形的底是2，∵函数y=ax2+bx+c的最小值是y=﹣2，∴平行四边形的高是2，∴阴影部分的面积是：2×2=4，∴结论③正确；∵，c=﹣1，∴b2=4a，∴结论④正确．综上，结论正确的是：③④．故答案为：③④．点评：（1）此题主要考查了二次函数的图象与几何变换，要熟练掌握，解答此类问题的关键是要明确：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．（2）此题还考查了二次函数的图象与系数的关系，要熟练掌握，解答此题的关键是要明确：①二次项系数a决定抛物线的开口方向和大小：当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；②一次项系数b和二次项系数a共同决定对称轴的位置：当a与b同号时（即ab＞0），对称轴在y轴左；当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）③常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．答案：。