西安电子科技大学数电答案第六章

第六章可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程，使之具有预定的逻辑功能，成为用户设计的ASIC芯片。

近年来，可编程逻辑器件从芯片密度上、速度上发展相当迅速，已成为集成电路的一个重要分支。

本章要求读者了解PLD器件的工作原理，掌握用可编程逻辑器件设计数字电路的方法。

为掌握使用电子设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。

第一节基本知识、重点与难点一、基本知识（一）可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、可编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。

它们的组成和工作原理基本相似，其基本结构由与阵列和或阵列构成。

与阵列用来产生有关与项，或阵列把所有与项构成“与或”形式的逻辑函数。

在数字电路中，任何组合逻辑函数均可表示为与或表达式，因而用“与门－或门”两级电路可实现任何组合电路，又因为任何时序电路是由组合电路加上存储元件（触发器）构成的，因而PLD的“与或”结构对实现数字电路具有普遍意义。

（二）可编程逻辑器件分类1.按编程部位分类PLD有着大致相同的基本结构，根据与阵列和或阵列是否可编程，分为三种基本类型：（1）与阵列固定，或阵列可编程；（2）与或阵列均可编程；（3）与阵列可编程，或阵列固定。

2.按编程方式分类（1）掩膜编程；（2）熔丝与反熔丝编程；（3）紫外线擦除、电可编程；（4）电擦除、电可编程；（5）在系统编程（Isp）。

（三）高密度可编程逻辑器件HDPLD单片高密度可编程逻辑器件HDPLD（High Density Programmable Logic Device）芯片内，可以集成成千上万个等效逻辑门，因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。

HDPLD器件在结构上仍延续GAL的结构原理，因而还是电擦写、电编程的EPLD 器件。

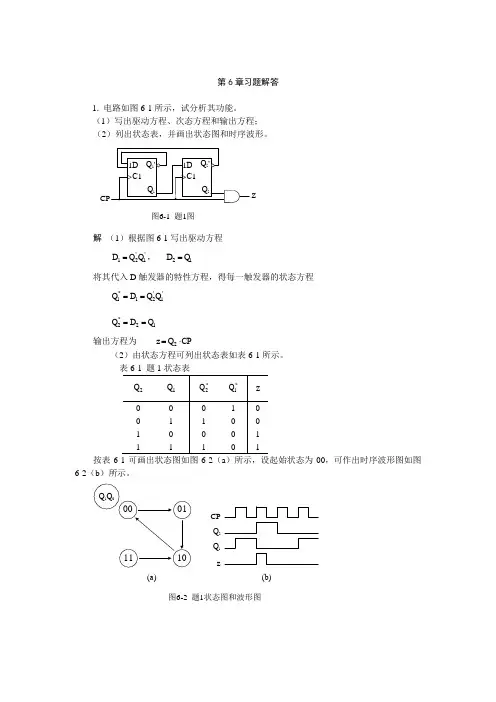
第6章习题解答1. 电路如图6-1所示，试分析其功能。

（1）写出驱动方程、次态方程和输出方程；（2）列出状态表，并画出状态图和时序波形。

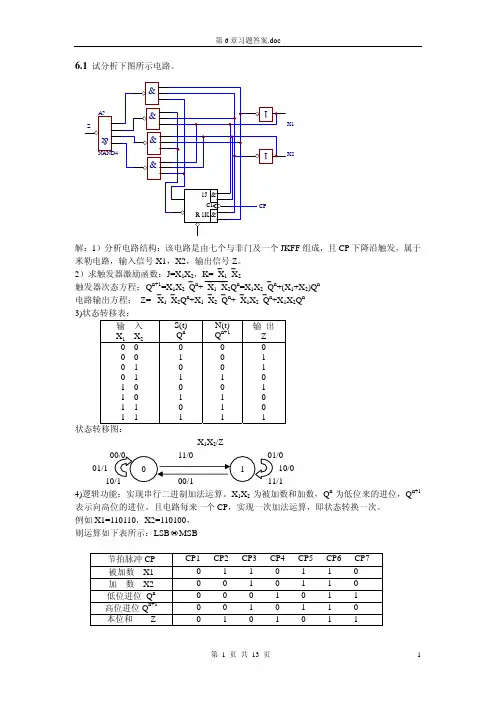
图6-1 题1图z解 （1）根据图6-1写出驱动方程'1'21Q Q D =， 12Q D =将其代入D 触发器的特性方程，得每一触发器的状态方程'1'21*1Q Q D Q ==12*2Q D Q ==输出方程为 CP Q z ⋅=2（2）由状态方程可列出状态表如表6-1所示。

按表00，可作出时序波形图如图6-2（b ）所示。

图6-2 题1状态图和波形图CP Q 2Q 1z(a )(b )2. 时序电路如图6-3所示。

（1）写出该电路的状态方程、输出方程；（2）列出状态表，画出状态图。

图6-3 题2图解 （1）驱动方程 x K J ==11 122xQ K J ==将其代入JK 触发器的特性方程，的状态方程21'21*21'1*1)'('Q xQ Q xQ Q Q x xQ Q +=+=输出方程 21Q xQ z =（2）假定一个现态，代入状态方程，得出对应的次态和输出状态，列表表示即得状态表，如表6-2所示。

由此算出状态图，如图6-4所示。

表6-2 题2状态表图6-4 题2的状态图3. 某计数器的输出波形如图6-5所示，试确定该计数器是模几计数器，并画出状态图。

图6-5 题3图CP Q A Q B QC解 由波形图画出状态图，Q C 为高位，Q A 为最低位。

010000001100011101Q C Q B Q A故该波形显示的计数器的计数模为六。

4. 分析如图6-6所示的同步时序电路。

图6-6 题4图解 （1）有题图得到各级触发器的驱动方程为⎪⎪⎩⎪⎪⎨⎧====34231242'3'11)'(Q D Q D Q D Q Q Q Q D（2）列出状态方程为⎪⎪⎩⎪⎪⎨⎧========34*423*312*242'3'11*1)'(Q D Q Q D Q Q D Q Q Q Q Q D Q由驱动方程和状态方程可以确定，该电路是移位寄存器型时序电路，其电路的状态转移决定于第一级的驱动信号。

弟八早可编程逻辑器件PLD可编程逻辑器件PLD是由用户借助计算机和编程设备对集成电路进行编程，使Z具有预定的逻辑功能，成为用户设计的ASIC芯片。

近年来，可编程逻辑器件从芯片密度上、速度上发展相当迅速，已成为集成电路的一个重要分支。

本章耍求读者了解PLD器件的丄作原理，掌握用可编程逻辑器件设计数字电路的方法。

为学握使用电了设计自动化和可编程逻辑器件设计电路系统的后续课程打下良好的基础。

第一节基本知识、重点与难点一、基本知识（一）可编程逻辑器件PLD基本结构可编程逻辑器件PLD包括只读存储器ROM、对编程只读存储器PROM、可编程逻辑阵列PLA、可编程阵列逻辑PAL、通用阵列逻辑GAL和可擦写编程逻辑器件EPLD等。

它们的组成和工作原理基本相似，其基本结构由与阵列和或阵列构成。

与阵列用來产生有关与项，或阵列把所有与项构成“与或”形式的逻辑函数。

在数字电路中，任何组合逻辑函数均可表示为与或表达式，因而用“与门一或门”两级电路可实现任何组合电路，乂因为任何时序电路是由组合电路加上存储元件（触发器）构成的，因而PLD的“与或”结构对实现数字电路具冇普遍意义。

（二）可编程逻辑器件分类1.按编程部位分类PLD冇着大致相同的棊木结构，根据与阵列和或阵列是否可编程，分为三种基木类型:（1）与阵列固定，或阵列可编程；（2）与或阵列均nJ编程；（3）与阵列可编程，或阵列固定。

2.按编程方式分类（1）掩膜编程；（2）熔丝与反熔丝编程；（3）紫外线擦除、电可编程；（4）电擦除、电可编程；（5）在系统编程（Isp）o（三）高密度可编程逻辑器件HDPLD单片高密度「|J编程逻辑器件HDPLD （High Density Programmable Logic Device）芯片内，可以集成成千上万个等效逻辑门，因此在单片高密度可编程逻辑器件内集成数字电路系统成为可能。

HDPLD器件在结构上仍延续GAL的结构原理，因而还是电擦写、电编程的EPLD 器件。

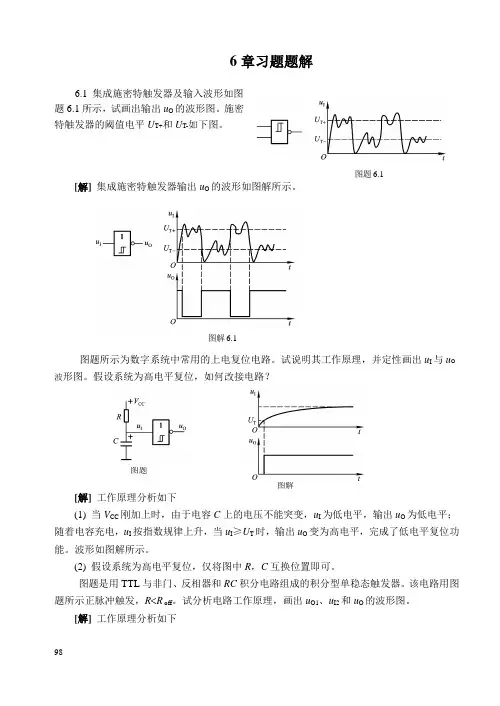
6章习题题解6.1 集成施密特触发器及输入波形如图题6.1所示，试画出输出u O的波形图。

施密特触发器的阈值电平U T+和U T-如下图。

图题6.1 [解]集成施密特触发器输出u O的波形如图解所示。

图解6.1图题所示为数字系统中常用的上电复位电路。

试说明其工作原理，并定性画出u I与u O 波形图。

假设系统为高电平复位，如何改接电路？图题图解[解] 工作原理分析如下(1) 当V CC刚加上时，由于电容C上的电压不能突变，u I为低电平，输出u O为低电平；随着电容充电，u I按指数规律上升，当u I≥U T时，输出u O变为高电平，完成了低电平复位功能。

波形如图解所示。

(2) 假设系统为高电平复位，仅将图中R，C互换位置即可。

图题是用TTL与非门、反相器和RC积分电路组成的积分型单稳态触发器。

该电路用图题所示正脉冲触发，R R off。

试分析电路工作原理，画出u O1、u I2和u O的波形图。

[解]工作原理分析如下9899触发信号未到来时，u I 为低电平，输出u O 为高电平；正触发脉冲到来时，u O1翻为低电平，此时由于u I2仍为高电平，输出u O 为高电平不变，电容通过R 放电，当u I2下降到U T 时〔u I 仍为高电平〕，输出u O 翻为高电平，暂稳态过程结束。

u O1、u I2和u O 的波形见图解。

6.4 集成单稳态触发器74121组成的延时电路如图题6.4所示，要求 (1)计算输出脉宽的调节范围； (2)电位器旁所串电阻有何作用？[解] (1) 输出脉宽：W ext ext W 0.70.7()t R C R R ==+,分别代入R W =0和22k Ω计算，可得t W的调节范围为：W 3.6mS 19mS t ≤≤。

(2) 电阻R 起保护作用。

假设无R ，当电位器调到零时，假设输出由低变高，那么电容C 瞬间相当于短路，V CC 将直接加于内部门电路输出而导致电路损坏。

6.5 集成单稳态触发器74121组成电路如图题6.5所示，要求(1)计算u O1、u O2的输出脉冲宽度；(2)假设u I 如图中所示，试画出输出u O1、u O2的波形图。

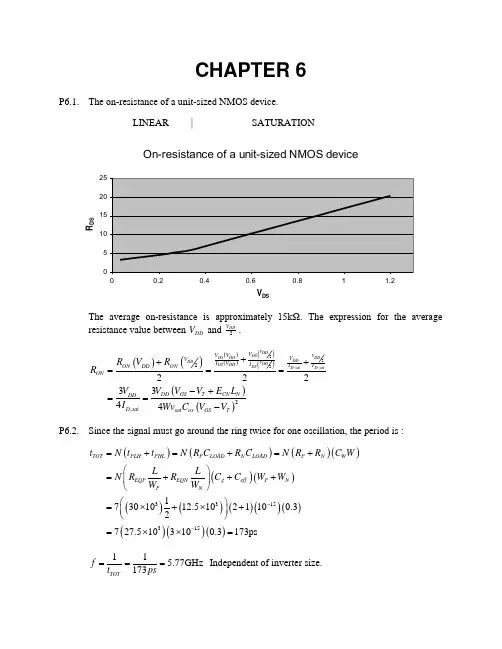
CHAPTER 6P6.1. The on-resistance of a unit-sized NMOS device.LINEAR | SATURATIONOn-resistance of a unit-sized NMOS device051015202500.20.40.60.811.2V DSR D SThe average on-resistance is approximately 15kΩ. The expression for the average resistance value between DD V and 2DDV .()()()()()()()()222,,22,2223344V DD DSV DS DD DDDD DDV DDDS DD DS D satD satV V V V V I V I I ON DD ON ON DD GS T CN N DDD sat sat ox GS T R V R R V V VE L V I Wv C V V +++===-+==-P6.2. Since the signal must go around the ring twice for one oscillation, the period is :()()()()()()()()()()()()()()331531517301012.51021100.32727.5103100.3173ps TOT PLH PHL P LOAD N LOAD P N W EQP EQN g eff P N P N t N t t N R C R C N R R C W L L N R R C C W W W W --=+=+=+⎛⎫=+++ ⎪⎝⎭⎛⎫=⨯+⨯+ ⎪⎝⎭=⨯⨯=115.77GHz 173TOTf t ps=== Independent of inverter size.P6.3. SPICE.P6.4. The self-capacitance in these cases are the capacitances that will make the transition from0 to DD V or vice versa.a. In this case, all the internal nodes will be charged so the self-capacitance is :()2233313SELF eff eff C C W W W W W C W =++++=b. In this case, all the internal nodes but the one above the bottom NMOS transistor will be charged:()223310SELF eff eff C C W W W W C W =+++=c. If we assume a worst-case scenario, this node will be charged up to DD V from 0.()2233313SELF eff eff C C W W W W W C W =++++=d. The node above the bottom-most NMOS transistor has already been discharged.()223310SELF eff eff C C W W W W C W =+++=P6.5. SPICEP6.6. For optimum sizing given four inverters.()()()()()()()()()()()()44332214111111120012005.8911200203.895.891203.8934.645.89134.64 5.895.8915.8915.8945.890.525.5OUT NPE LE FO SE LE C C SE LE C C SE LE C C SE LE C C SE D LE FO P SE P =⨯=====⨯===⨯===⨯===⨯====⨯+=+=+=∏∑∑For the number of devices for optimum delay:log log log log log log12005.11log log 4N N SE SE PE SE PE N SE PEPE N SE =======Setting 5N =gives:()()()()()()()()5544332215114.1211200290.634.121290.6370.394.12170.3917.054.12117.05 4.124.1214.1214.1244.120.518.5OUT N SE LE C C SE LE C C SE LE C C SE LE C C SE LE C C SE D LE FO P SE P ===⨯===⨯===⨯===⨯===⨯====⨯+=+=+=∑∑P6.7. Solution for NAND3For the first NAND3, LE=5W/3W=5/3. For the second NAND3, the delay is not the same asthe basic inverter. So use the more general formula:310/25/33nand W R LE WR⨯== Same as the first case.a.For equal rise and fall time, we double the sizes of the transistors which leads to:313LE==b.For the pseudo-NMOS, we must first calculate the currents, which are different forpull-up and pull-down in the case of a pseudo-NMOS.For the case of the pull-up, only the PMOS is charging the output, for equal delays,we double the size of the PMOS and NMOS to obtain:23LE=P6.9.a.53 LE=b.53 LE=c.82,33 R FLE LE==d.4,23R FLE LE==P6.10.a.813RLE st gate =b.523FLE nd gate =()()()()()()()()()()()()()()45343433221411451110002222336.8711000145.656.87145.6535.366.8735.36 6.876.871 6.8716.8746.870.51 1.50.5OUT NN N PE LE FO SE LE C C SE LE C C SE LE C C SE LE C C SE D SE P SE P ⎛⎫⎛⎫=⨯== ⎪⎪⎝⎭⎝⎭===⨯===⨯===⨯===⨯====+=+=++++∏∑∑31=P6.12.()()()()()()()()()()()()()()()6345434332211546410001777833311.5510001173.2111.55173.2112511.5525411.5511.55111.551111.55OUT N N PE LE FO BE SE LE C BE C SE LE C BE C SE LE C BE C SE LE C BE C SE D SE P ⎛⎫⎛⎫⎛⎫=⨯⨯== ⎪⎪⎪⎝⎭⎝⎭⎝⎭===⨯⨯===⨯⨯===⨯⨯===⨯⨯====+∏()()41411.550.51 1.5251.2N SE P =+=++++=∑∑()()()()()()()()()()()635735445712(2)(4)800066730333314.6800011095.814.610951175.114.64512(4175.1500)533533OUT PE LE FO BE SE LE C BE C SE LE C BE C SE PE LE FO BE SE ⎛⎫⎛⎫⎛⎫=⨯⨯== ⎪⎪⎪⎝⎭⎝⎭⎝⎭===⨯⨯===⨯⨯===⎛⎫⎛⎫=⨯⨯=⨯+= ⎪⎪⎝⎭⎝⎭==∏∏()()()()()()()()()()()5343322151117.4712001114.317.54114.32317.517.5117.51117.53(17.5)214.60.51 1.5 2.25288.9NN N LE C BE C SE LE C BE C SE LE C BE C SE D SE P SE P =⨯⨯===⎛⎫⎪⨯⨯⎝⎭===⨯⨯====+=+=++++++=∑∑To minimize the delay, a estimate of the number of needed stages can be performed :log log 6637049.610log log 4SE PE N SE =∴===≈ The additional stages can be implemented as inverters attached at the input.P6.14. Consider the following situations :C LV inC LV outOutput high-to-low Output low-to-highIn the first case, the output is making a transition from high to low. The next inverter (not shown) has the PMOS in the cutoff region and the NMOS in the linear region. In these regions, the input capacitance of the next gate can be computed as follows:PMOS: C GP =C g x 2W x (1/2) NMOS: C GN =C g x WFor the output low-to-high transition, we have the PMOS linear and the NMOS cutoff: PMOS: C GP =C g x 2W NMOS: C GN =C g x W (1/2)Clearly, the second case has a larger total capacitance and hence a larger effective C g .P6.15. For this problem we examine ramp inputs as compared to step inputs. In both cases below,the transistors being driven enter the linear region and experience larger gate capacitances than the step input case. Therefore, C g is always larger for ramp inputs.C LC LV outpositive-going input ramp negative-going input rampV V DDP6.16. The FO4 delay for 0.18um is approximately 75ps. For 0.13um it is 55ps. Therefore, theconstant for the equation is roughly 420ps/um.。

习题4 4－3解：该电路的输入为3x 2x 1x 0x ，输出为3Y 2Y 1Y 0Y 。

真值表如下：由此可得：1M =当时，33232121010Y x Y x x Y x x Y x x =⎧⎪=⊕⎪⎨=⊕⎪⎪=⊕⎩ 完成二进制至格雷码的转换。

0M =当时，332321321210321010Y x Y x x Y x x x Y x Y x x x x Y x =⎧⎪=⊕⎪⎨=⊕⊕=⊕⎪⎪=⊕⊕⊕=⊕⎩ 完成格雷码至二进制的转换。

4－9 设计一个全加（减）器，其输入为A,B,C 和X （当X ＝0时，实现加法运算；当X ＝1时,实现减法运算),输出为S(表示和或差），P(表示进位或借位）。

列出真值表，试用3个异或门和3个与非门实现该电路，画出逻辑电路图。

解：根据全加器和全减器的原理,我们可以作出如下的真值表:由真值表可以画出卡诺图，由卡诺图得出逻辑表达式，并画出逻辑电路图:A B C XP4－10 设计一个交通灯故障检测电路，要求红，黄，绿三个灯仅有一个灯亮时,输出F ＝0；若无灯亮或有两个以上的灯亮，则均为故障，输出F ＝1。

试用最少的非门和与非门实现该电路。

要求列出真值表，化简逻辑函数，并指出所有74系列器件的型号. 解:根据题意，我们可以列出真值表如下：对上述的真值表可以作出卡诺图，由卡诺图我们可以得出以下的逻辑函数：F AB AC BC ABC AB AC BC ABC =+++=•••逻辑电路图如下所示：A F4－13 试用一片3－8译码器和少量逻辑门设计下列多地址输入的译码电路.（1） 有8根地址输入线7A ~1A ,要求当地址码为A8H,A9H ，…,AFH 时，译码器输出为0Y ～7Y 分别被译中，且地电平有效。

（2） 有10根地址输入线9A ～0A ，要求当地址码为2E0H,2E1H, …,2E7H 时，译码器输出0Y ~7Y 分别被译中，且地电平有效.解：(1）当122100A B E E E =，即75364210111,00,A A A A A A A A ==从000～111变化时07~Y Y 分别被译中，电路如下图所示：Y Y (2）当122100A B E E E =，即97538432101111,000,A A A A A A A A A A ==从000～111变化时，07~Y Y 分别被译中。

思考题与习题6-1已知图T6-1所示为施密特触发器输入信号u I 的波形，请对应画输出信号u O 的波形。

图T6-16-2 在如图6-14所示的单稳态触发器电路中，已知R=10k Ω、C=0.1μF ，G 1的输出 电阻可忽略不计，试估算输出波形u O 的脉冲宽度。

代入得，脉宽t w=0.7ms6-3图T6-3所示电路是用两个集成单稳态触发器74121构成的脉冲波形变换电路，试计算u O1和u O2输出脉冲的宽度，并画出对应于u I 的u O1和u O2波形。

图T6-3RCt w 7.06-4图T6-4所示电路为可控多谐振荡器，已知tW等于振荡器输出脉冲周期的5倍，请对应u k画u O1和u O2的波形。

图T6-46-5试构成一个如图6-23所示的RC环形振荡器电路，要求振荡器输出信号的频率为1kHZ ，请估算R和C的数值。

若要求振荡频率为1HZ，则R和C又该为多少？解：T≈2.2RC，f=1KHZ，则T=1ms，因此，当f=1KHZ时，RC=0.45ms；当f=1HZ 时，RC=0.45s。

6-6试用555定时器构成一个单稳态电路，要求输出脉冲幅度≥10V，输出脉冲宽度在1-10秒范围内连续可调。

解：根据题意，用555定时器设计得单稳态触发器取R1=22K,R2=18K，分压后输入端电压为6.75V(电源电压为15V），一般的，555定时器得输出高电平不低于其电源电压得90%，因此选15v.则UO输出脉宽t W=1.1RC设C=1000μF,则1≤1.1R×1000×10-6≤ 10 909≤R ≤9K6-7图T6-7是用两个555定时器接成的延迟报警器。

当开关S 断开后，经过一定的延 迟时间后扬声器开始发出声音。

如果在延迟时间内S 重新闭合，扬声器不会发出 声音。

在图中给定的参数下，试求延迟时间的具体数值和扬声器发出声音的频率。

图中的G 1是CMOS 反相器，电源电压为12V 。

6.2 试作出101序列检测器得状态图，该同步电路由一根输入线X ，一根输出线Z ，对应与输入序列的101的最后一个“1”，输出Z=1。

其余情况下输出为“0”。

（1） 101序列可以重叠，例如：X ：010101101 Z ：000101001 （2） 101序列不可以重叠，如：X ：010******* Z ：0001000010 解：1）S 0：起始状态，或收到101序列后重新开始检测。

S 1：收到序列起始位“1”。

S 2：收到序列前2位“10”。

10101…X/Z0/01/0X/Z11…100…2）10101…X/Z0/0X/Z11…100…6.3对下列原始状态表进行化简：(a)解：1）列隐含表：A B CDC B ×A B CD C B ×AD BC ××(a)(b)2）进行关联比较 所有的等价类为：AD ，BC 。

最大等价类为：AD ，BC ，重新命名为a,b 。

3）列最小化状态表为：a/1b/0bb/0a/0aX=1X=0N(t)/Z(t)S(t)(b)N （t ）/Z （t ）S （t ）X=0 X=1A B/0 H/0B E/0 C/1C D/0 F/0D G/0 A/1E A/0 H/0F E/1 B/1G C/0 F/0H G/1 D/1解：1）画隐含表：2）进行关联比较：AC,BD,EG ,HF,之间互为等价隐含条件，所以分别等价。

重新命名为： a, b, e, h 3)列最小化状态表：N （t ）/Z （t ） S （t ）X=0 X=1a b/0 h/0b e/0 a/1 e a/0 h/0 h e/1 b/1试分析题图6.6电路，画出状态转移图并说明有无自启动性。

解：激励方程：J1=K1=1；J2=Q1n⎯Q3n，K2=Q1nJ2=Q1n Q2n，K2=Q1n状态方程：Q1n+1=⎯Q1n·CP↓Q2n+1=[Q1n⎯Q3n⎯Q2n+⎯Q1n Q2n]·CP↓Q3n+1=[Q1n Q2n⎯Q3n+⎯Q1n Q3n]·CP↓状态转移表：序号Q3Q2Q10 1 2 3 4 5 000 001 010 011 100 101偏离状态110Æ111111Æ000状态转移图状态转移图：Q3Q2Q1偏离态能够进入有效循环，因此该电路具有自启动性。

西安电子科技大学网络教育考试题（1）课程名称：_数字电路 考试形式： 开 卷学习中心：_________ 考试时间： 90分钟姓 名：_____________ 学 号：一、单项选择题（本大题共15小题，每小题2分，共30分）在每小题列出的四个备选项中只有一个是符合题意要求的，请将其选出并将“答题卡”的相应代码涂黑。

未涂、错涂或多涂均无分。

1．下列数中最大的数是A ．(1.1)8B ．(1.1)16C ．(1.1)10D ．(1.1)2 2．八进制数(76)8所对应的8421BCD 码是A ．(10010010)8421BCDB ．(01110110)8421BCDC ．(01100010)8421BCD D ．(10000100)8421BCD3．某逻辑电路输入A 、B 和输出F 的波形如图1.1所示，由此判断该门电路完成的逻辑功能是A ．与非B ．异或C ．同或D ．或非4．图1.2所示电路的输出函数F 的表达式为 A ．C B B A F += B ．C B B A F += C ．C B B A F += D ．C B B A F += 5．某函数BD C A B A F ++⋅=反函数为A ．)()(DBC A B A F +++= B ．)()(D B C A B A F +++= C ．)()(D B C A B A F ++++= D ．D B C A B A F +++=)( 6．AC C A B A F ++=的最简表达式为A B F图1.1A ．B A B ．C A C ．A B +D ．1 7．函数C A B A F +=的最小项标准式为 A ．∑=)7,6,2,0()(ABC F B ．∑=)5,4,3,1()(ABC F C ．∑=)5,3,2,0()(ABC F D ．∑=)7,5,3,1()(ABC F8．n 变量的逻辑相邻项有A ．2n 个B ．2n 个C ．n 2个D ．n 个 9．逻辑函数D C B A D B C A F ⋅++⋅+=的最简与或式是 A ．BC D A + B ．D C B A D B C A ⋅++⋅+ C ．C B D A ⋅+ D ． D B C B + 10．∑=)11,9,4,3,1,0()(ABCD F ，约束条件为0=+BD AB ，其最简与或非式为A ．DBC A F +⋅= B ．F A CD =⋅+ C ．D C D A F += D ．D C D A F += 11．函数))((C B A C A F +++=的最简与非式是A ．CB AC A F ⋅= B ．C A B A AC F ⋅⋅⋅⋅= C ．AC AB C A F ⋅⋅⋅=D ．BC A C A F ⋅= 12．将一路信号送至多个输出端，应选用A ．译码器B ．数据选择器C ．编码器D ．数据分配器 13．为了使D 触发器实现T 触发器功能，则激励端D 应接至A ．0=DB ． nQ D = C ．nQ D = D ．1=D14．用555定时器构成的典型施密特电路，其外接电源V U DD 18=则其回差电压为 A ．V U T 6=∆ B ．V U T 12=∆ C ．V U T 16=∆ D ．V U T 18=∆ 15．为了将模拟信号转换为数字信号，应选用A ．数字/模拟转换电路B ． 模拟/数字转换电路C ．译码器D ．移位寄存器二、填空题（本大题共5小题，每小题2分，共10分）16．十进制数19的余3代码是 。

第六章 习题解答6.1. 分析题图P6.1所示电路的功能，列出功能表。

解：图P6.1所示电路的功能表如表6.1所示。

将功能表中各变量数值关系的逻辑函数用对应的“卡诺图”如图6.1所示。

RS 具有约束条件RS ＝0，触发器的逻辑表达式为⎪⎩⎪⎨⎧=+=+0RS Q R S Q n 1n ，根据这一逻辑表达式，P6.1逻辑电路具有基本RS 触发器的逻辑功能，约束条件是SR=0。

6.2同步RS 触发器与基本RS 触发器的主要区别是什么？解：同步RS 触发器与基本RS 触发器的主要区别是基本RS 触发器的RS 输入信号不论任何时刻都是有效的，只要RS 输入的状态组合发生变化，输出Q 的状态跟随发生变化；而同步同步RS 触发器的RS 输入信号只要在CP 时钟脉冲信号有效时段内起作用，只有在这一时段内，输出Q 的状态才跟随RS 输入的状态组合变化而发生变化。

1& & 1QR图 P6.1QR S Q nQ n+1功 能 1 1 1 1 0 1 不用 不用 不允许11 0 0 0 1 0 0 01=+n Q 置0 0 0 1 1 0 1 1 1 11=+n Q 置10 00 00 10 1n n Q Q =+1 保持6.3如图P6.3 (a)所示电路的初始状态为Q =1，R 、S 端和CP 端的信号如图P6.3（b ）所示，画出该同步RS 触发器相应的Q 和Q 端的波形。

解：根据图P6.3 (a)所示电路结构，其功能为同步RS 触发器，电路的特性方程为：⎪⎩⎪⎨⎧=+=+0RS Q R S Q n 1n ，若R=S=1，在CP 时钟脉冲信号为“1”的时段内，触发器的两个输出端的状态均输出“1”，此种情况下，若CP 时钟脉冲信号从“1”状态，跳变为“0”的输入状态，则触发器的两个输出状态为不确定状态。

根据特性方程以及电路的初始状态，作出电路的输出端时序图如图6.3所示。

6.4 主从RS 触发器输入信号的波形如图P6.4（a ）、（b ）所示。

西安电子科技大学版数字电子技术(第三版)第六章时序逻辑电路1.解：状态迁移图计数器的计数模为六。

2.（1）由所给方程画出逻辑图(2)该电路是异步电路，对异步电路的分析，主要注意每一级触发器的时钟。

对Q2、Q3而言，因为其J=K=1，每一时钟下降沿必翻转，即在Q1由1→0时，Q2翻转一次；同样，Q2由1→0时，Q3翻转一次。

为了判断电路的计数模，应先作出状态迁移表。

该电路为一个具有自启动能力的异步模九计数器(3) 由上述状态迁移表，可画出状态迁移图，如图所示。

2. 解 由波形图直接得状态迁移关系。

由此可看出该计数器是一个同步模六递减计数器。

由状态迁移表、作出卡诺图，从而求得各级触发器的特征方程，再与JK 触发器特征方程n nn Q K Q J Q+=+1相比较，即可得激励方程：nAn B nC A nAB nAC A n Cn A B nB n AC nAn A nB n A nB nC nA nB n Cn A nC nB nA n C Q Q Q C K Q K Q K J Q Q J Q Q J Q Q Q Q Q Q Q Q Q Q Q Q Q Q ========+=+=+++11111迁移表卡诺图 如选D 触发器，则激励方程为：nAnB nC nAA n CnA n Bn A B n Cn A nC n B n A C nAn A nCnA nB n A n B n Cn A nC nB nA n C Q Q Q C Q D QQ Q Q D QQ Q Q Q D Q Q Q Q Q Q Q Q Q Q Q Q Q ==+=+==+=+=+++111由激励方程画出逻辑图。

D 触发器电路图。

最后还应检验自启动能力： 110→011； 111→110 显然该电路具有自启动能力。

3. 解：写出方程 激励方程：nnn Q Q D Q D 21211⊕==特征方程：nnn n n Q Q Q Q Q 2112111⊕==++状态真值表状态迁移图该电路为同步四进制加法计数器。