尺寸链计算(带实例)

L AB / X A ﹦ 0.999 ； L AB
/ X B ﹦ 0.999 ； LAB Y A ﹦ 0.0439 ；
7
L AB YB ﹦﹣0.0439
由上述各偏导数值的符号可知， X A 、 X B 和 Y A 是尺寸链的増环，
YB 是减环。
' ' ⑵ 计算公差 d X A 、d X B 、d Y A' 和 d YB' ' ' 由式⑷可得：d LAB ﹦ LAB X A d X A ﹢ LAB X B d X B ﹢ ' L AB Y A d Y A ﹢ LAB YB d YB' ' ' 已知：d LAB ﹦0.18mm ；所以：0.18﹦｜0.999｜d X A ﹢｜0.999｜d X B ' ' ﹢｜0.0439｜d Y A ' ﹢｜﹣0.0439｜d YB' ；取 d X A ﹦d X B ﹦d Y A' ﹦d YB' ' ' ' ' 则 dXA ﹦d X B ﹦d Y A' ﹦d YB' ﹦0.086mm﹙说明：可以取 d X A 、d X B 、d Y A'
代入上式，即
' 0.18﹦｜0.999｜d X A ﹢｜0.999∣ 0.072﹢∣0.0439∣d Y A' + ' ' ｜﹣0.0439｜ 0.072 ；取 d X A ﹦d Y A' ，则 d X A ﹦d Y A' ﹦0.1mm；由于 ' ' dXA 和 d Y A' 小于 d X A 和 d Y A ，所以 d X A 和 d Y A 应取 d X A 和 d Y A' 之值， ' 即 d X A ﹦d Y A ﹦d X A ﹦d Y A' ﹦0.1mm。综上所述，可得：d X B ﹦d YB

添加文档副标题
目录
01.
02.
03.
04.
05.
Байду номын сангаас
尺寸链：由一组相互关联的尺寸组成的封闭尺寸组 装配尺寸链：在产品装配过程中用于保证产品功能要求的尺寸链 组成：封闭的尺寸组由一个或多个零件的尺寸和位置关系组成 作用：用于控制和保证产品装配精度确保产品功能要求
组成元素：零件尺寸、公差和 其它因素
计算步骤：确定封闭环、列出尺寸链中的所有组成环、对所有组成环进行定性和定量的分析、根据需要 选择合适的计算方法（如极值法或概率法）进行计算。
实例说明：以某机械装配为例需要保证两个零件和B之间的距离为10mm已知零件的孔距为10mm零件 B的孔距为10.05mm通过简单的尺寸链计算可以确定零件和零件B之间的装配关系。
选择合适的计算方法
打开软件并导入装配尺寸链 数据
输入相关参数并进行计算 查看计算结果并进行调整
应用领域：机械、建筑、电 子等工程设计领域
软件名称：uCD
功能特点：具备强大的绘图、 编辑、标注等功能支持多种文
件格式导入导出
应用实例：某机械部件装配尺 寸链计算通过软件实现快速准
确的计算和分析
目的：确定各零件尺寸和公差 之间的关系
建立方法：根据零件之间的装 配关系列出尺寸链图
作用：确保产品装配精度和性 能
确定封闭环 判断组成环的性质
查找组成环 建立尺寸链线图
定义：极值法是 一种确定装配尺 寸链的方法通过 确定各零件尺寸 的极值来计算装 配尺寸链。
适用范围：适用 于零件尺寸变化 范围较大或对装 配精度要求较高 的装配尺寸链计 算。
结论：通过简单装配尺寸链计算可以确定零件之间的装配关系保证产品性能和精度要求。

公差尺寸链计算公式公差尺寸链公差尺寸链是指由一系列零件组成的装配体系中，各零件之间的公差关系。

在机械设计和生产过程中，正确的计算和控制公差尺寸链是确保装配质量的重要因素。

下面列举一些相关的计算公式，并给出解释和例子。

1. 最大材料条件与最小材料条件最大材料条件（MMC）是指零件或特征的最大尺寸，而最小材料条件（LMC）是指零件或特征的最小尺寸。

根据这两个条件，在公差尺寸链的计算中，我们可以得到以下两个公式：•最大材料条件下公差尺寸：T = MMC - 低限制公差•最小材料条件下公差尺寸：T = LMC - 高限制公差以螺纹为例，最大材料条件下，螺纹轴的最大尺寸为25 mm，低限制公差为- mm，那么螺纹轴的最大材料条件下公差尺寸为 mm（25 + (-)）。

2. 链公差法则在公差尺寸链的计算中，使用链公差法则可以将公差传递从装配体到各个零件，下面是链公差法则的一般形式：T(a, b) = T(a) + T(b) + |∑L|其中，T(a, b)是装配体尺寸的公差，T(a)和T(b)分别是零件a和b的公差，∑L是两个零件直接的公差和（所有相邻公差的代数和），也称为“累加和”。

以一个简单的装配体为例，该装配体由两个零件a和b组成，零件a的公差为 mm，零件b的公差为 mm。

两个零件的直接公差和为 mm。

根据链公差法则，装配体的公差尺寸为：T(a, b) = + + || = mm3. 频率分布法则在公差尺寸链的计算中，使用频率分布法则可以根据具体的公差分布情况，计算出装配体尺寸的公差。

以下是频率分布法则的一般形式：T = ΔD × K其中，ΔD是公差限制域（公差分布范围的一半），K是概率累积函数曲线的系数。

以一个简单的零件为例，假设公差限制域为 mm，概率累积函数曲线的系数为。

那么该零件的公差尺寸为：T = × = mm总结•最大材料条件与最小材料条件可用于计算公差尺寸。

•链公差法则可用于将公差传递到装配体。

概率法尺寸链计算范例
假设我们有一个尺寸链，包括尺码为S、M、L、XL、XXL的商品。

每个尺码的出货频率如下：
S：0.2
M：0.3
L：0.4
XL：0.08
XXL：0.02
首先，我们需要计算每个尺码的累计概率。

S：0.2
M：0.5 (0.2 + 0.3)
L：0.9 (0.2 + 0.3 + 0.4)
XL：0.98 (0.2 + 0.3 + 0.4 + 0.08)
XXL：1 (0.2 + 0.3 + 0.4 + 0.08 + 0.02)
接下来，我们选择一个0到1之间的随机数。

假设我们选择了0.75。

我们需要找到这个随机数所在的尺码。

0.75落在L和XL之间，因为L的累计概率为0.9，XL的累计概率为0.98，0.75在这两个数之间。

因此，我们可以选择L或XL。

我们选择L。

因此，当我们选择一个0.75的随机数时，我们会得到尺码为L的商品。

这就是概率法尺寸链计算的基本过程。

我们可以使用相同的方法计算其他随机数所对应的尺码。

显然，第三个尺寸链给分的公差最小，的公差就可按尺寸链3来定。 （即的公差为0.042mm）。当的公差确定后，的偏差布置是根据尺寸 链1中的布置方式来分布（即mm，和设计尺寸mm的布置形式是一致 的）。
3. 计算其余的工序尺寸及偏差
1. 由尺寸链计算公式：
2. 封闭环的基本尺寸＝所有增环的基本尺寸－所有减环的基本尺寸；
图1 设计尺寸
作业3 如图2－40所示为某模 板简图，镗削两孔O1, O2时 均以底面M为定位基准，试标 注镗两孔的工序尺寸。检验两 孔孔距时，因其测量不便，试 标注出测量尺寸A的大小及偏 差。若A超差，可否直接判定 该模板为废品？
作业3 下图所示轴套 工件，在车床上已加工 好外圆、内孔及各表面， 现需在铣床上以端面A 定位铣出表面C，保证 尺寸20-0.2mm试计算 铣此缺口时的工序尺寸。
2. 基本尺寸计算：43.6=A+20－19. 8mm
3. A＝43．4
4. 上偏差计算：+0. 34=Bs(A)＋0. 025－0
5. Bs (A)＝＋0. 315mm
6. 下偏差计算：0=B,(A)+0－0. 05
7. Bx (A)＝＋0. 05mm
8. 所以
A=43.4+0.05+0.315mm
作业4 要求在轴上铣一 个键槽，如下图所示。加 工顺序为车削外圆A1＝； 铣键槽尺寸为A2；磨外 圆A3＝Ø70-00.06mm， 要求磨外圆后保证键槽尺 寸为N＝62-00.3mm,求 键槽尺寸A2。
整体活动预期
3. 封闭环的上偏差＝所有增环的上偏差－所有减环的下偏差；
4. 封闭环的下偏差＝所有增环的下偏差－所有减环的上偏差。
5. 计算尺寸链2 得mm

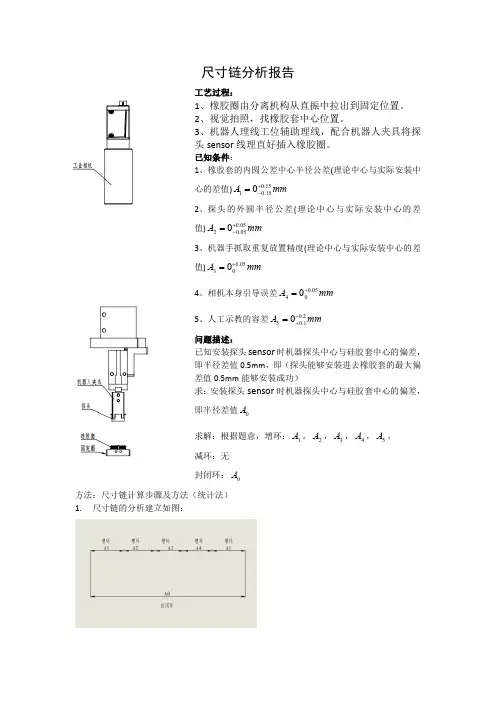
尺寸链分析报告工艺过程：1、橡胶圈由分离机构从直振中拉出到固定位置。

2、视觉拍照，找橡胶套中心位置。

3、机器人理线工位辅助理线，配合机器人夹具将探头sensor 线理直好插入橡胶圈。

已知条件：1、橡胶套的内圆公差中心半径公差(理论中心与实际安装中心的差值)mmA 15.015.010+-=2、探头的外圆半径公差(理论中心与实际安装中心的差值)mmA 05.005.020+-=3、机器手抓取重复放置精度(理论中心与实际安装中心的差值)mmA 05.0030+=4、相机本身引导误差mm A 05.0040+=5、人工示教的容差mmA 2.01.050++=问题描述：已知安装探头sensor 时机器探头中心与硅胶套中心的偏差，即半径差值0.5mm ，即（探头能够安装进去橡胶套的最大偏差值0.5mm 能够安装成功）求：安装探头sensor 时机器探头中心与硅胶套中心的偏差，即半径差值0A 求解：根据题意，增环：1A ，2A ，3A ，4A ，5A ，减环：无封闭环：0A 方法：尺寸链计算步骤及方法（统计法）1.尺寸链的分析建立如图：2.计算封闭环的基本尺寸：封闭环的基本尺寸等于所有增环的基本尺寸和减去所有减环的基本尺寸和。

0=A 3.计算封闭环的公差：批量生产条件下，组成环与封闭环的实际偏差均服从正态分布，且实际尺寸分布范围与公差带宽度一致。

此时，封闭环的公差平方值等于所有组成环公差平方值之和。

4.0,16.01.005.005.01.03.0,02222220252423222120==++++=++++=T T T T T T T T 公差：公差：公差：4.计算封闭环的中间偏差。

封闭环中间偏差等于所有增环中间偏差之和减去所有减环中间偏差之和。

注：中间偏差等于上下偏差代数和再除以2.2.0,15.0025.0025.000,00543210=∆++++=∆∆+∆+∆+∆+∆=∆中间偏差：中间偏差：中间偏差：5.计算封闭环的极限偏差。

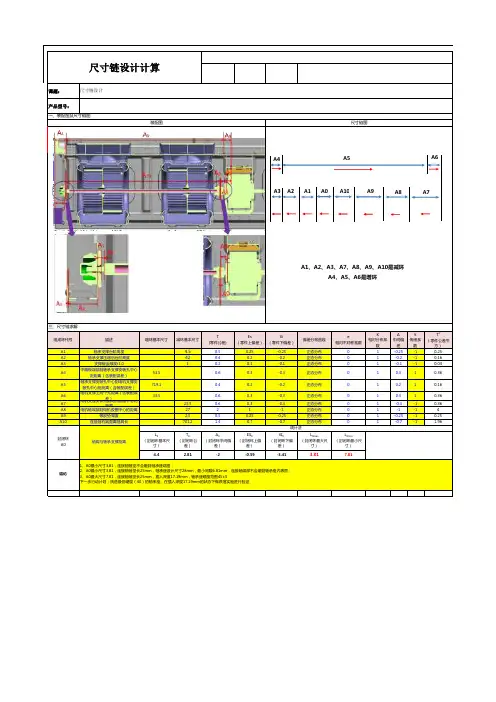
课题：产品型号：组成环代号描述增环基本尺寸减环基本尺寸T(零件公差)Es（零件上偏差）Ei（零件下偏差）偏差分布曲线e相对不对称系数K相对分布系数∆中间偏差§传递系数T （零件公差平方）A1轴承支撑台阶高度 4.50.50.25-0.25正态分布01-0.25-10.25A2轴承支撑压缩后台阶高度420.40.2-0.2正态分布01-0.2-10.16A3支撑钣金厚度t1.010.20.1-0.1正态分布01-0.1-10.04A4中隔板端部到轴承支撑安装孔中心距距离（含装配误差）53.50.60.3-0.3正态分布010.310.36A5轴承支撑安装孔中心到电机支撑安装孔中心距距离（含装配误差）719.10.40.2-0.2正态分布010.210.16A6电机支撑上两个孔距离（含装配误差）33.50.60.3-0.3正态分布010.310.36A7电机支座安装孔到电机胶圈中心的距离23.50.60.3-0.3正态分布01-0.3-10.36A8电机轴端部到电机胶圈中心的距离2721-1正态分布01-1-14A9橡胶垫厚度 2.50.50.25-0.25正态分布01-0.25-10.25A10连接轴右端面离轴肩长701.2 1.40.7-0.7正态分布1-0.7-11.96L 0（封闭环基本尺寸）T 0（封闭环公差）∆0（封闭环中间偏差）ES 0（封闭环上偏差）EI 0（封闭环下偏差）L （封闭环最大尺寸）L （封闭环最小尺寸）4.4 2.81-2-0.59-3.413.817.81结论尺寸链设计计算三、尺寸链求解统计法1、A0最小尺寸3.81，连接轴轴坚不会磨到轴承座端面；2、A0最小尺寸3.81，连接轴轴坚长25mm，轴承座设计尺寸28mm，最小间隙6.81mm，连接轴端部不会磨到轴承座内表面；3、A0最大尺寸7.81，连接轴轴坚长25mm，插入深度17.19mm，轴承座硬度范围45±5下一步行动计划：挑选最低硬度（40）的轴承座、在插入深度17.19mm的状态下做跌落实验进行验证封闭环A0轴肩与轴承支撑距离尺寸链设计一、装配图及尺寸链图装配图尺寸链图A2A4A1、A2、A3、A7、A8、A9、A10是减环A4、A5、A6是增环A1A0A10A9A7A8A3A6A5。

尺寸链公差计算案例摘要：一、引言二、尺寸链公差计算方法1.尺寸链概念2.尺寸链公差计算公式3.尺寸链公差计算实例三、尺寸链公差在工程中的应用1.零件加工中的应用2.产品设计中的应用四、总结正文：一、引言在机械制造领域，尺寸链公差计算是一项基础且重要的工作。

尺寸链是由一系列相互关联的尺寸组成的，它们在加工和装配过程中相互影响。

为了保证产品的质量和性能，掌握尺寸链公差的计算方法至关重要。

本文将详细介绍尺寸链公差的计算方法及其在工程中的应用。

二、尺寸链公差计算方法1.尺寸链概念尺寸链是指在零件加工和装配过程中，由一系列相互关联的尺寸组成的链式结构。

这些尺寸之间存在一定的相对位置关系，并相互影响。

尺寸链的公差是指各个尺寸之间的允许偏差范围。

2.尺寸链公差计算公式尺寸链公差计算公式为：T=max(Δi)+min(Δj)其中，T表示尺寸链的公差，Δi表示第i个尺寸的允许偏差，Δj表示第j 个尺寸的允许偏差。

3.尺寸链公差计算实例以一个简单的尺寸链为例，假设有一个零件的尺寸分别为A、B、C，它们的允许偏差分别为±0.1mm、±0.2mm、±0.3mm。

根据公式，可以计算出尺寸链的公差为：T=max(ΔA, ΔB, ΔC)+min(ΔA, ΔB,ΔC)=0.3mm+0.1mm=0.4mm。

三、尺寸链公差在工程中的应用1.零件加工中的应用在零件加工过程中，尺寸链公差计算有助于确定加工工艺和检验标准。

根据尺寸链公差，加工人员可以合理选择加工设备和工艺参数，以确保零件加工质量。

2.产品设计中的应用在产品设计阶段，尺寸链公差计算有助于优化设计方案，提高产品的可靠性和性能。

设计人员可以根据尺寸链公差，合理设置产品的尺寸参数，使其在满足功能要求的同时，具有良好的制造性和装配性。

四、总结尺寸链公差计算在机械制造领域具有重要的意义。

掌握尺寸链公差的计算方法，有助于保证产品的质量和性能，提高制造过程的效率。

尺寸链公差计算案例
尺寸链公差计算是一种通过逐级加工和配合来确定零件尺寸的方法。

以下是一个尺寸链公差计算的案例：
假设要计算一个由两个零件组成的尺寸链的公差。

零件A是一个圆柱体，直径为30mm，长度为50mm。

零件B是一个与零件A配合的孔，直径为30.1mm，长度为50mm。

首先，我们需要确定两个零件之间的配合公差。

配合公差是由设计要求和制造工艺决定的。

如果要求零件A与零件B之间具有一定的间隙，可以选择一个负公差，如果要求零件A与零件B之间具有一定的紧配合，可以选择一个正公差。

假设我们选择一个-0.05mm的配合公差。

接下来，我们需要确定零件A和零件B的尺寸公差。

尺寸公差是由制造工艺和产品要求决定的。

在这个案例中，我们假设零件A和零件B的尺寸公差都是±0.02mm。

最后，我们可以计算出整个尺寸链的公差。

尺寸链公差等于零件A的直径公差加上零件B的直径公差再加上配合公差。

在这个案例中，尺寸链公差=±0.02mm + ±0.02mm + (-0.05mm) = ±0.19mm。

这样，我们就确定了这个尺寸链的公差为±0.19mm。

根据这个公差，我们可以在制造过程中控制零件的尺寸，以确保零件的配合满足要求。

尺寸链公差计算案例
假设我们要计算一条尺寸链的公差，该尺寸链包含4个零件距离，它们是A、B、C和D。

首先，我们需要明确每个零件的尺寸和公差。

假设A的尺寸
为10mm，公差为±0.1mm；B的尺寸为15mm，公差为
±0.2mm；C的尺寸为20mm，公差为±0.3mm；D的尺寸为
25mm，公差为±0.1mm。

接下来，我们需要计算每个零件的尺寸范围。

对于A零件来说，其下限是10 - 0.1 = 9.9mm，上限是10 + 0.1 = 10.1mm。

同样地，B的下限是15 - 0.2 = 14.8mm，上限是15 + 0.2 =
15.2mm；C的下限是20 - 0.3 = 19.7mm，上限是20 + 0.3 = 20.3mm；D的下限是25 - 0.1 = 24.9mm，上限是25 + 0.1 = 25.1mm。

然后，我们可以计算尺寸链整体的下限和上限。

下限是各个零件下限之和，即9.9 + 14.8 + 19.7 + 24.9 = 69.3mm；上限是各
个零件上限之和，即10.1 + 15.2 + 20.3 + 25.1 = 70.7mm。

最后，我们可以得到尺寸链的公差范围。

公差是上限减去下限，即70.7 - 69.3 = 1.4mm。

因此，该尺寸链的公差为±1.4mm。

这只是一个简单的尺寸链公差计算案例，实际情况可能更加复杂，需要考虑更多的零件和更多的尺寸限制。

环名 2L2（增环） 增环）
基本尺寸 上偏差 下偏差 66 -0.15 -0.28
最后结果：L 2 = 33−0..075 mm − 0 140
4．有表面处理工序的工艺尺寸链计算 表面处理是指表面渗碳﹑渗氮等渗入类以及镀 铬﹑镀锌等镀层类的表面处理。渗入类表面处 理通常在精加工以前完成渗入，精加工后应使 渗入层厚度符合设计要求，因此设计要求的渗 入层厚度为封闭环。镀层类表面处理在大多数 情况下是通过控制电镀工艺参数来保证镀层厚 度的，因此最后获得的电镀后的零件尺寸为封 闭环。
工艺尺寸链的应用
例2. 图所示零件，设计尺寸为10-0.360。因尺寸不便测量， 图所示零件，设计尺寸为10 A0 = A − A 改测尺寸x。试确定尺寸x的数值和公差。 z =1 z j = n +1 j
n m
∑
n
∑
解： 1）列尺寸链 B A 2）判断各环性质 X
ES 0 = ∑ ES z −
z =1
下偏差 +0.04 0 -0.015 0 0
0 结果：A 1 = 43.1+0..16 = 43.140.12 mm + 0 04
例4. 连杆厚度尺寸要求如图所示。为了使连杆在加工过程中安装方便，开始加 工时小头的厚度亦按大头要求加工，到加工后期再将小头铣薄。有关的加 工工序如下：
30±0.1
a）
下偏差 +0.025 0 0 0
R1（减环） 键槽深度H为磨内孔间接 R1（减环） 得到，是封闭环。其余各 D1/2 环的判断如图。 H（封闭环） 封闭环）
3）计算
+ 最后结果为 : A1 = 43.1+0..175 = 43.125 0 0.15 mm + 0 025

专题二、 工艺尺寸链
一、尺寸链的定义、组成
1、定义
尺寸链就是在零件加工或 机器装配过程中,由相互 联系且按一定顺序连接的 封闭尺寸组合。
（1）在加工中形成的尺寸链——工艺尺寸链
2.定位面 3.设计基准
1.加工面
A1 A0 A2
（2）在装配中形成的尺寸链——装配尺寸链
A0 A2 A1
图示工件如先以A面定位加工C面,得尺寸A1然后再以A
举例:
增环
A1 A0 A2
A3
封闭环
减环
二、尺寸链的分类
1、按应用范围分类
1）工艺尺寸链——全部组成环为 同一零件工艺尺寸所形成的尺寸链。 2）装配尺寸链——全部组成环为 不同零件设计尺寸所形成的尺寸链。 3）零件尺寸链——全部组成环为同 一零件设计尺寸所形成的尺寸链。 4）设计尺寸链——装配尺寸链与零 件尺寸链,统称为设计尺寸链。
求解图4-206和图4-26c的尺寸链，可得到：
工序尺寸：A 235 0 0..2 1534.90 0.15
平行度公差：Ta2 0.05
2）测量基准与设计基准不重合的尺寸换算☆ ☆ ☆
【例 4-2】图 4-30 所 示 零 件 , 尺 寸
A0不好测量,改测尺寸A2 ,试确定 A2的大小和公差。
【解】A2是测量直接得到的尺 寸，是组成环；A0是间接保 A0 1000.36
中间计算可用于设计计算与工艺计算,也可用于验算。
4. 确定组成环公差大小的误差分配方法
1） 等公差原则 按等公差值分配的方法来分配封闭环的公差 时,各组成环的公差值取相同的平均公差值Tav:即 极值法 Tav=T0/（n-1）
概率法 TavT0 / n1
这种方法计算比较简单,但没有考虑到各组成环加工的难易、 尺寸的大小,显然是不够合理的。

尺寸链计算例题
尺寸链计算是一种用于计算物体尺寸关系的方法，其中一个物体的尺寸可以通过另一个物体的尺寸和比例关系来推导出来。

以下是一个尺寸链计算的例题：
问题：一个正方形纸片的边长为3厘米，将其对角线分割成两段，其中一段的长度是另一段长度的2倍，求两段的长度。

解答：首先，我们知道对角线可以将正方形分割成两个等边三角形。

设其中一段的长度为x厘米，则另一段的长度为2x厘米。

根据勾股定理，正方形的边长的平方等于对角线的两段长度的平方之和。

因此，有：
3^2 = x^2 + (2x)^2
9 = x^2 + 4x^2
9 = 5x^2
x^2 = 9 / 5
x = √(9/5)
因为边长不能为负数，所以x = √(9/5) ≈ 1.34。

因此，其中一段的长度约为1.34厘米，另一段的长度约为2.68厘米。

尺寸链公差计算案例摘要：I.尺寸链公差计算的背景和意义II.尺寸链公差计算的案例分析A.计算公式和基本概念B.具体案例分析1.组成环的确定2.公差的计算3.结果分析III.尺寸链公差计算在实际应用中的优势和意义正文：尺寸链公差计算在机械加工领域具有重要的意义。

在产品设计和制造过程中，通过计算尺寸链公差，可以保证产品的加工精度和质量，优化工艺路线，减少资源浪费和降低产品的返修率。

本文将通过一个具体的案例分析，详细介绍尺寸链公差计算的方法和步骤。

首先，我们需要了解尺寸链公差计算的基本概念和公式。

尺寸链公差计算是基于组成环和封闭环的概念。

组成环是指直接保证产品尺寸的各个环节，而封闭环则是间接保证产品尺寸的环节。

尺寸链公差的计算公式为：上偏差= 所有增环的上偏差之和- 所有减环的下偏差之和；下偏差= 所有增环的下偏差之和- 所有减环的上偏差之和。

接下来，我们通过一个具体的案例来分析尺寸链公差计算的过程。

假设有一个产品，其尺寸为100mm，公差要求为±1mm。

我们需要计算组成环和封闭环，以及公差。

1.组成环的确定：组成环是直接保证产品尺寸的环节。

在这个案例中，组成环为直接加工的环节，即加工100mm 的环节。

因此，组成环为100mm。

2.公差的计算：根据公式，我们可以计算出上偏差和下偏差。

上偏差= 100mm * 1mm = 100mm；下偏差= 100mm * (-1mm) = -100mm。

3.结果分析：根据计算结果，我们可以得出产品尺寸的上偏差为100mm，下偏差为-100mm。

这意味着在加工过程中，产品的尺寸可以在100mm 的基础上增加100mm，或者减少100mm，仍能满足公差要求。

尺寸链公差计算在实际应用中具有很大的优势。

通过计算公差，工程师可以在设计和制造过程中更好地掌握产品的尺寸变化，优化工艺路线，减少浪费和返工。

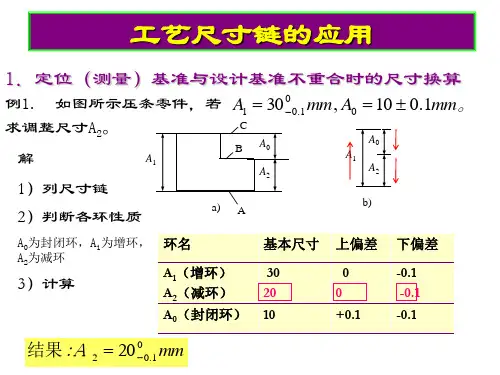
第五章 工艺规程设计例1:图示零件,2面设计尺寸为 2522.00 +mm ，尺寸60012.0-mm 已经保证，现以1面定位用调整法精铣2面，试计算工序尺寸。

解:(1)建立尺寸链设计尺寸2522.00 +mm 是间接保证的，是封闭环，A 1（60012.0-mm ）和A 2为组成环。

（2）计算根据 A 0＝∑=m i i A 1－∑-+=11n m i i A A 2 = A 1－A 0＝35ES 0＝∑=mi i ES 1－∑-+=11n m i i EI EI 2＝ES 1－ES 0＝－0.22 EI 0＝∑=mi i EI 1－∑-+=11n m i i ES ES 2＝EI 1－EI 0＝－0.12则：工序尺寸A 2＝3512.022.0--＝34.88010.0-mm 。

例2:下图所示工件外圆、内孔及端面均已加工完毕，本序加工A 面，保证设计尺寸8±0.1 mm 。

由于不便测量，现已B面作为测量基准，试求测量尺寸及其偏差。

解:（1）建立尺寸链设计尺寸8±0.1是mm 是封闭环，A 1、A 2、A 3是组成环。

（2）计算根据 A 0＝∑=m i i A 1－∑-+=11n m i i AA 1 = A 0－A 2＋A 3=18ES 0＝∑=m i i ES 1－∑-+=11n m i i EI ES 1=ES 0－ES 2＋EI 3=0EI 0＝∑=mi i EI 1－∑-+=11n m i i ES EI 1=EI 0－EI 2＋ES 3=－0.05 则：测量尺寸A 1＝180 05.0-＝17.9505.00 ＋ mm 。

例3：一带有键槽的内孔要淬火及磨削，其设计尺寸如图所示。

保证键槽尺寸034 0436..+ mm 的有关工艺过程如下： 1）镗内孔至中01 0396..ϕ＋（005 0198.R .＋）mm ； 2）插键槽至尺寸A 1；3）淬火（变形忽略不计）；4）磨内孔，同时保证内孔直径005 040.ϕ+（0025 020.R +）mm 和键槽深度 034 0436..+mm 两个设计尺寸的要求。

51-0.4
50-0.34
10.4-0.2
零件图
10 车孔及端面
14.6±0.2
20 车外圆及端面
10-0.3
30 钻孔
40 磨外圆及台阶
解:1)分析
从零件图上看,设计尺寸有10-0.3mm、15±0.2mm 以及50-0.34。 根据工艺过程分析是否全部达到图纸要求.其中10-0.3、 50-0.34直 接保证,15±0.2间接保证,为封闭环,必须校核。
m
n 1
n 1
T ( A 0 ) i 1 T ( A i) i m 1 T ( A i) i 1 T ( A i)
极值法解算尺寸链的特点是: 简便、可靠,但当封闭环公差较小,组成环数目较多时, 分摊到各组成环的公差可能过小,从而造成加工困难,制造 成本增加,在此情况小,常采用概率法进行尺寸链的计算。
该尺寸链中,H0 是最 终的渗碳层深度,是间
接保证的,因而是封闭
环。计算该尺寸链,可
得到:
a)
H1 0.700..02058
图4-33 渗碳层深度尺寸换算b)
2021/3/28
28
4. 多尺寸保证时的尺寸换算
例4-5 如图所示轴套,其加工工序如图所示,试校验 工序尺寸标注是否合理。
10-0.3
50-0.34 15±0.2
尺寸链方程
—— 确定尺寸链中封闭环（因变量） 和组成环（自变量）的函数关系式,其一般形 式为:
A 0f(A 1,A 2, ,A n)
2021/3/28
11
工艺尺寸链示例:
工件A、C 面已加工好,现以A 面定位用 调整法加工B 面,要求保证B、C 面距离A0
0.05 A C B

3）.按各环尺寸的几何特征分
（1）长度尺寸链 示。 （2）角度尺寸链 如图12—1，图12—2所 如图12—3所示。
4、尺寸链的建立
1）.确定封闭环
装配尺寸链的封闭环是在装配之后形成的，往往是 机器上有装配精度要求的尺寸，如保证机器可靠工作的 相对位置尺寸或保证零件相对运动的间隙等。 零件尺寸链的封闭环应为公差等级要求最低的环， 如图12-1b中尺寸B0是不标注的。 工艺尺寸链的封闭环是在加工中自然形成的，一般 为被加工零件要求达到的设计尺寸或工艺过程中需要的 尺寸。 一个尺寸链中只有一个封闭环。
6、解算尺寸链的方法
1. 完全互换法（极值法） 完全互换法是尺寸链计算中最基本的方法。 2. 不完全互换法（概率法） 采用概率法，不是在全部产品中，而是在绝大多 数产品中，装配时不需挑选或修配，就能满足封闭环 的公差要求，即保证大多数互换。 与完全互换法相比，在封闭环公差相等的情况下， 不完全互换法可使用组成环的公差扩大，从而获得良 好的技术经济效益，也比较科学合理，常用在大批量 生产的情况。 3.其他方法
封闭环的重要性: (1) 体现在尺寸链计算中，若封闭环判断错误，则全部分 析计算之结论，也必然是错误的。 (2) 封闭尺寸是通过其他尺寸要间接保证的尺寸。通常是 产品技术规范或零件工艺要求决定的尺寸。 在装配尺寸链中，封闭环往往代表装配中精度要求的尺 寸；而在零件中往往是精度要求最低的尺寸，通常在零件图 中不予标注。
3.画尺寸链线图 为清楚地表达尺 寸链的组成，通常不 需要画出零件或部件 的具体结构，只需将 尺寸链中各尺寸依次 画出，形成封闭的图 形即可，这样的图形 称为尺寸链线图，如 图12-4b所示。
5、解算尺寸链的任务
（1）正计算 已知各组成环的极限尺寸，求封 闭环的尺寸。 （2）反计算 已知封闭环的极限尺寸和各组成 环的基本尺寸，求各组成环的极限偏差。 （3）中间计算 已知封闭环和部分组成环的极 限尺寸，求某一组成环的极限尺寸。