下载文档原格式
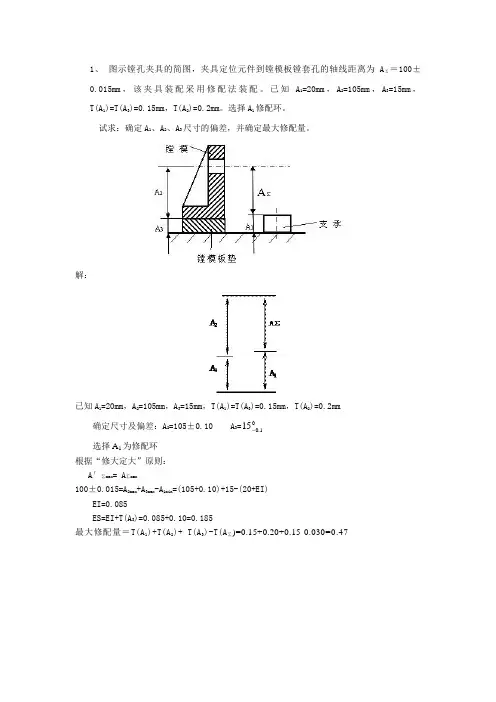
1、 图示镗孔夹具的简图，夹具定位元件到镗模板镗套孔的轴线距离为A Σ＝100±0.015mm ，该夹具装配采用修配法装配。
已知A 1=20mm ，A 2=105mm ，A 3=15mm ，T(A 1)=T(A 3)=0.15mm ，T(A 2)=0.2mm 。
选择A 1修配环。
试求：确定A 1、A 2、A 3尺寸的偏差，并确定最大修配量。
解：已知A 1=20mm ，A 2=105mm ，A 3=15mm ，T(A 1)=T(A 3)=0.15mm ，T(A 2)=0.2mm确定尺寸及偏差：A 2=105±0.10 A 3=01.015选择A 1为修配环根据“修大定大”原则：A ′∑max = A ∑max100±0.015=A 2max +A 3max -A 1min =(105+0.10)+15-(20+EI)EI=0.085ES=EI+T(A 3)=0.085+0.10=0.185最大修配量＝T(A 1)+T(A 2)+ T(A 3)-T(A ∑)=0.15+0.20+0.15-0.030=0.472.如图a 所示的结构，已知各零件的尺寸：A1= mm ，A2=A5= mm ，A3= mm ，A4= mm 设计要求间隙A 。
为0.1～0.45mm ，试做校核计算。
解:（l ）确定封闭环为要求的间隙A0；寻找组成环并画尺寸链线图（图2b ）；判断A3为增环，A1、A2、A4和A5为减环。
（2）按公式计算封闭环的基本尺寸A0＝A3一（A1+A2+A4+A5）=43mm —（30+5+3+5）mm=0即要求封闭环的尺寸为0+0.45 +0.10mm 。
（3）按公式计算封闭环的极限偏差ES 。
=ES3一（EI1+EI2+EI4+EI5）=＋0.18mm 一（一0.13—0.075—0.04—0.075）mm=＋0.50mmEI 。
=EI3一（ES1+ES2+ES4+ES5）=＋0.02mm —（0＋0＋0＋0）mm=＋0.02mm（4）按公式计算封闭环的公差T 。
一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中，由相互联系的尺寸,按一定顺序排列成的封闭尺寸组，称为尺寸链。
尺寸链示例2、工艺尺寸链的组成环：工艺尺寸链中的每一个尺寸称为尺寸链的环。
工艺尺寸链由一系列的环组成。
环又分为：（1）封闭环（终结环）：在加工过程中间接获得的尺寸，称为封闭环。
在图b所示尺寸链中，A0是间接得到的尺寸，它就是图b所示尺寸链的封闭环。
（2）组成环：在加工过程中直接获得的尺寸，称为组成环。
尺寸链中A1与A2都是通过加工直接得到的尺寸，A1、A2都是尺寸链的组成环。
1）增环：在尺寸链中，自身增大或减小，会使封闭环随之增大或减小的组成环，称为增环。
表示增环字母上面用--> 表示。
2）减环：在尺寸链中，自身增大或减小，会使封闭环反而随之减小或增大的组成环，称为减环。
表示减环字母上面用<-- 表示。
3）怎样确定增减环：用箭头方法确定，即凡是箭头方向与封闭环箭头方向相反的组成环为增环，相同的组成环为减环。
在图b所示尺寸链中，A1是增环，A2是减环。
4）传递系数ξi：表示组成环对封闭环影响大小的系数。
即组成环在封闭环上引起的变动量对组成环本身变动量之比。
对直线尺寸链而言，增环的ξi＝1，减环的ξi＝－1。
3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。
已知组成环求封闭环的计算方式称作正计算；已知封闭环求各组成环称作反计算；已知封闭环及部分组成环，求其余的一个或几个组成环，称为中间计算。
尺寸链计算有极值法与统计法（或概率法）两种。
用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。
用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。
5.极值法解尺寸链的计算公式（4）封闭环的中间偏差（5）封闭环公差（6）组成环中间偏差Δi＝(ES i＋EI i)/2（7）封闭环极限尺寸（8）封闭环极限偏差6.竖式计算法口诀：封闭环和增环的基本尺寸和上下偏差照抄；减环基本尺寸变号；减环上下偏差对调且变号。
内容提纲1、装配尺寸链1装配尺寸链2、保证机器装配精度的方法2保证机器装配精度的方法当遇到有些要求较高的装配精度，如果完全靠相关零件的制造精度来直接保证，则零件的加工精度将会很高，给加工带来较大困难。
一、装配尺寸链1.装配尺寸链的概念装配尺寸链是以某项装配精度指标（或装配要求）作为封闭环，查找所有与该项精度指标（或装配要求）有关零件的尺寸（或位置要求）作为组成环而形成的尺寸链。
☞装配尺寸链的封闭环、组成环●封闭环：是间接保证的。
装配尺寸链的封闭环→产品或部件的装配精度要求。
如装配间隙、过盈量、装配后的位置要求。
一个装配精度要求就可以建立一个装配尺寸链。
●组成环：对装配精度要求有直接影响的那些零、部件上的尺寸和位置关系。
分为增环和减环（定义及判断方法同工艺尺寸链）。
2. 装配尺寸链的分类◆分类：根据各环的几何特征及所处的空间位置线性尺寸链→所有环为长度或精度的尺寸链，各环→所有环为长度或精度的尺寸链各环位于同一平面且彼此平行。
角度尺寸链→垂直度、平行度等平面尺寸链空间尺寸链装配尺寸链的建立步骤建3. 装配尺寸链的建立步骤一般按下列步骤建立尺寸链。
1、确定封闭环2、查找组成环(1)查找相关零件(2)确定相关零件上的相关尺寸3、画尺寸链图并确定组成环的性质（1）几何公差环的特点何差几何公差环可看做公称尺寸为零的尺寸环。
若几何公差的上、下极限偏差对称分布，如同轴度和对称度等那么无论把该环定为增环是减环它们对封称度等，那么无论把该环定为增环还是减环，它们对封闭环的影响将是相同的。
因此，上、下极限偏差对称分布的几何公差环，可以不必判定其是增环还是减环，任意假定都可以。
若几何公差的上下极限偏差虽是对称分布而若几何公差的上、下极限偏差虽是对称分布，而实际上是只允许单向极限偏差的环，那么就必须判定其是增环还是减环并限制其出现另一方向的极限偏差还是减环，并限制其出现另一方向的极限偏差。
判定方法见角度尺寸链。
（2）配合间隙环的特点间隙配合间隙环是指间隙配合时，因轴比孔小，引起轴的轴线和孔的轴线的偏移量。
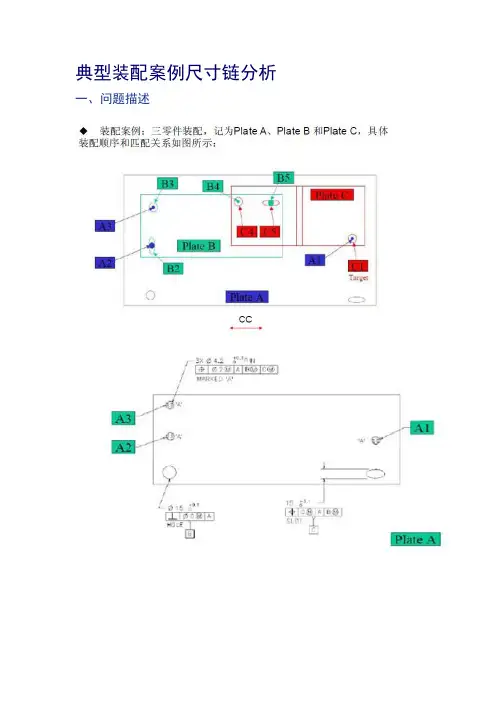
典型装配案例尺寸链分析一、问题描述
二、尺寸链计算
案例分析
1、本装配案例中，偏差的传递来源于两部分：各孔/销的尺寸公差与各
自的位置度公差。
通过A-B、B-C两次装配，偏差将会累积于C1孔，因此所求的C1孔差这些差值（大于
直径及其尺寸公应当包容偏的累计总等于）。
2、考虑到孔A 1、A3均位于Plate 上，A板本身的定位偏差将对两孔造成
A不独立的同向偏差传递，尺寸链中相互抵消，不予考虑。
3、由案例中的装配关系可以看出，Y向和X向的偏差传递方式相同，因此
只需考虑一个方向进行计算即可。
4、本例可利用极值法或概率法进行计算，极值法对偏差的要求更为
严格，
现假设各尺寸环符合正态分布，以生产中常用的概率法进行计算。
装配尺寸链计算-例2如图是一个齿轮装配结构图，由于齿轮要在轴上回转，要求装配后齿轮右端面与挡圈之间应留有0.2～0.45mm 的间隙。
已知A 1＝40mm ，A 2＝36mm ，A 3＝4mm ，设A 1、A 2、A 3的尺寸分布均为正态分布，试以不完全互换法解算各组成环的尺寸和极限偏差（公差等级及数值参考下表）。
标准公差数值（节选）公差等级基本尺寸/mm IT8 IT9 IT10 IT11IT12大于 至 公差值/μm－ 314 25 40 60 1003 6 18 30 48 75 120 6 10 22 36 58 90 150 10 18 27 43 70 110 180 18 30 33 52 84 130 210 30 50 39 62 100 160 250 50 80 46 74 120 190 300解：（1）作尺寸链，环数为4，A 0为封闭环，A 1为增环，A 2、A 3为减环。
（2）求封闭环的基本尺寸和公差()()0436403210=+−=+−=A A A A mm ()25.02.045.00=−=A T mm （2）求各组成环的公差()144.0325.010≈=−=n A T T av mm由于挡圈（A 3）易于制造，因此取它为协调环，A 1、A 2处于同一尺寸分段（30－50），取IT11级，即()()16.021==A T A T mm ，则()()()()106.02221203≈−−=A T A T A T A T mm ，取IT11级，即()075.03=A T mm（3）确定各组成环的极限偏差16.001401140+==H A mm ；016.02321132−==h A mm ()()08.02016.01=+=∆A mm ，()()08.0216.002−=−=∆A mm ，()()325.022.045.00=+=∆A mm∵()()()()3210A A A A ∆−∆−∆=∆，∴()()()()165.00213−=∆−∆−∆=∆A A A A mm()()()128.02333−=+∆=A T A A ES mm ，()()()203.02333−=−∆=A T A A EI mm所以，128.0203.034−−=A mm ，入体表示后得0075.03872.3−=A mm（4）核算封闭环的极限尺寸()()()()238.0075.016.022********≈+×=++=A T A T A T A T mm()()()444.02000=+∆=A T A A ES mm ，()()()206.02000=−∆=A T A A EI mm ，满足0.2～0.45mm 。
7.补偿环——尺寸链中预先选定某一组成环，可以通过改变其大小或位置，使封闭环达到规定的要求，该组成环为补偿环。
二、尺寸链的形成
为分析与计算尺寸链的方便，通常按尺寸链的几何特征，功能要求，误差性质及环的相互关系与相互位置等不同观点，对尺寸链加以分类，得出尺寸链的不同形式。
1.长度尺寸链与角度尺寸链
①长度尺寸链——全部环为长度尺寸的尺寸链
②角度尺寸链——全部环为角度尺寸的尺寸链
2.装配尺寸链，零件尺寸链与工艺尺寸链
①装配尺寸链——全部组成环为不同零件设计尺寸所形成的尺寸链
②零件尺寸链——全部组成环为同一零件设计尺寸所形成的尺寸链
③工艺尺寸链——全部组成环为同一零件工艺尺寸所形成的尺寸链。
工艺尺寸指工艺尺寸，定位尺寸与基准尺寸等。
装配尺寸链与零件尺寸链统称为设计尺寸链
装配尺寸链的解算示例
=（标准件）
封闭环的公称尺寸为零，即，先将各组
于内尺寸的组成环按基孔制，孔中心距按对称分布决定其极限偏差。
不过需要留一个组成环，其极限偏差确定后计算得到。
该组成环称为协调环。
此处A s为垫圈，容易加工，且其他尺寸都便于用通用量具测量，故选A s为协调环。
由此确定除协调环外各环的极限偏差
为:最后计算确定协调环
为: （2）不完全互换法。
采用不完全互换法时，装配尺寸链采用概率法公式计算。
当各组成环尺寸服从正态分布时封闭环公差T o
与各组成环公差T t的关系满足。
若各组成环尺寸不服从正态分
布，则取封闭环公差T o与各组成环公差T t的关系满足。
K依具体分布而定，一般可以取K=1.2~1.6。
仍然以图57-4所以示的装配关系简图是基本尺寸，装配精度要求为例，设各组成环尺寸服从一个标准件A4的尺寸链，取各组成环的平均公差T（mm）为:
一般平面装配尺寸链中，组成环对封闭环的误差传递系数的绝对值一般不等于1，需要先根据几何关系建立尺寸链方程后，再确定误差传递系数。
图57-8a为哥德式直线滚动导轨副的装配关系，图57-8b为一对沟槽的钢球接触关系。
该导轨副有四对沟槽，滑板与导轨轴各对沟槽的设计中心并不在同一点，分别位于图57-8a中的Xhi，Yhi和Xdi，Ydi(i=1,2,3,4),h表示滑板，d表示导轨轴。
装配后钢球在沟槽中的过盈量是主要的装配精度要求之一。
图57-8b所示为右上角一对沟槽的接触关系，单个哥德式沟槽的母线为两段对称的圆弧，圆弧的半径为R，圆心距离为yo。
记钢球设计尺寸为φo，实际尺寸为φ；钢球在单个沟槽中的压力角为ao，由于四对沟槽相互约束形成的压力角为a，设计尺寸△x、△y跟别表示两个沟槽中心在水平方向和垂直方向的距离，由图可见x=2（R-φo/2）cosao-△x、y=2（R-φo/2）sinao+△y。
在设计状态下，一对沟槽的四段圆弧的中心组成一个平行四边形，其对角线为相对两段圆弧的圆心连线。
装配时钢球与沟槽的接触点位于该平行四边形较长的那条对角线的延长线与圆弧的交点，即图中的U、T两点。
记钢球过盈量为C，以C为装配精度的尺寸链为：
作出图中的尺寸关系图，通常约定平行度的基本尺寸为oo，垂直度基本尺寸为90°，被检面相对基准面逆时针转动为正方向。
从封闭环的一条边开始，以其为基准面判断与相关的组成环变化对封闭环的影响。
再依次下一个的组成环对封闭环的影响，直至到封闭环的另一条边结束。
若先以图中燕尾导轨Ⅲ为基准面，床身V形导轨Ⅱ为被检面，判别a2变化对ao的影响。
当a2变大，Ⅱ相对Ⅲ逆时针转动时，带动主轴轴线Ⅰ也相对Ⅲ逆时针转动，ao变小，故a1也为减环。
依通常的基本尺寸约定，需要加上一个180°以使得尺寸链封闭，得到尺寸链方程为：。
