长、正方体思维导图
- 格式:ppt
- 大小:108.50 KB
- 文档页数:1
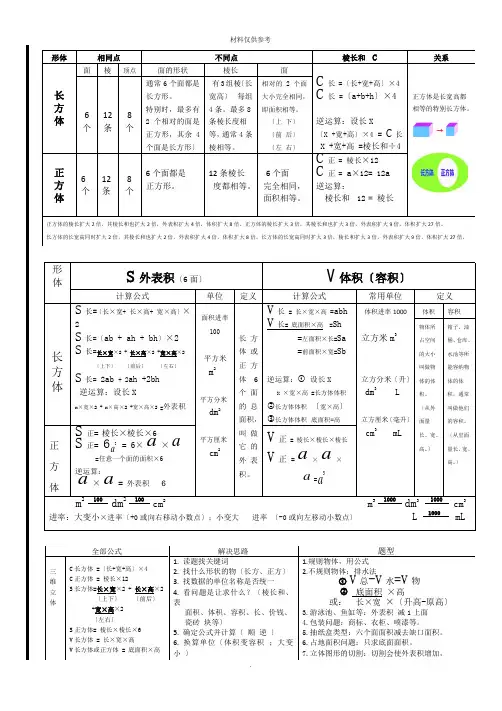
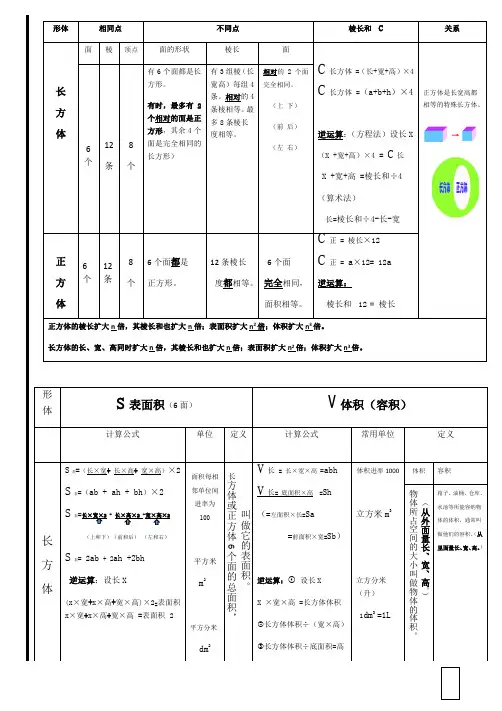
形体相同点不同点棱长和C关系长方体面棱顶点面的形状棱长面C长=〔长+宽+高〕×4C长 =〔a+b+h〕×4逆运算:设长X〔X +宽+高〕×4 = C长X +宽+高 =棱长和÷4正方体是长宽高都相等的特别长方体。
6个12条8个通常6个面都是长方形。
特别时,最多有2个相对的面是正方形,其余4个面是长方形〕有3组棱〔长宽高〕每组4条。
最多8条棱长度相等,通常4条棱相等。
相对的2个面大小完全相同,即面积相等。
〔上下〕〔前后〕〔左右〕正方体6个12条8个6个面都是正方形。
12条棱长度都相等。
6个面完全相同,面积相等。
C正= 棱长×12C正=a×12= 12a逆运算:棱长和÷12 = 棱长正方体的棱长扩大2倍,其棱长和也扩大2倍,外表积扩大4倍,体积扩大8倍。
正方体的棱长扩大3倍,其棱长和也扩大3倍,外表积扩大9倍,体积扩大27倍。
长方体的长宽高同时扩大2倍,其棱长和也扩大2倍,外表积扩大4倍,体积扩大8倍。
长方体的长宽高同时扩大3倍,棱长和扩大3倍,外表积扩大9倍,体积扩大27倍。
形体S外表积〔6面〕V体积〔容积〕计算公式单位定义计算公式常用单位定义长方体S长=〔长×宽+ 长×高+ 宽×高〕×2S长=〔ab + ah + bh〕×2S长=长×宽×2 + 长×高×2 +宽×高×2〔上下〕〔前后〕〔左右〕S长= 2ab+ 2ah +2bh逆运算:设长Xx×宽×2 + x×高×2 +宽×高×2 =外表积面积进率100平方米m2平方分米dm2平方厘米cm2长方体或正方体6个面的总面积,叫做它的外表积。
V长= 长×宽×高=abhV长= 底面积×高 =Sh=左面积×长=Sa=前面积×宽=Sb逆运算:①设长XX ×宽×高 =长方体体积②长方体体积÷〔宽×高〕③长方体体积÷底面积=高体积进率1000立方米m3立方分米〔升〕dm3 L立方厘米〔毫升〕cm3 mL体积容积物体所占空间的大小叫做物体的体积。
100 叫做它的表面积。
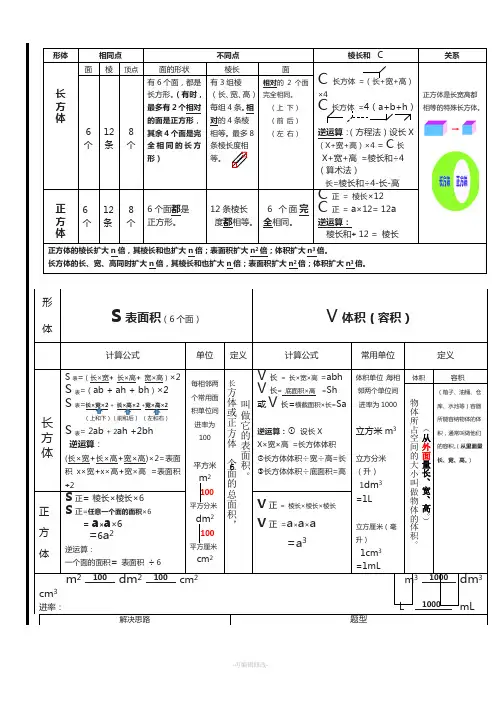
长方体或正方体个面的总面积,100形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C长方体 =(长+宽+高)×4C 长方体 =4(a+b+h )逆运算:(方程法)设长X(X+宽+高)×4 = C 长X+宽+高 =棱长和÷4 (算术法)长=棱长和÷4-长-高正方体是长宽高都相等的特殊长方体。
6个12 条 8 个有6个面,都是长方形。
(有时,最多有2个相对的面是正方形,其余4个面是完全相同的长方形)有3组棱(长、宽、高)每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
(上 下) (前 后) (左 右)正 方 体6个12条 8 个6个面都是 正方形。
12条棱长度都相等。
6个面完全相同。
C 正 = 棱长×12C 正 = a ×12= 12a逆运算:棱长和÷ 12 = 棱长正方体的棱长扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
形体S 表面积(6个面)V 体积(容积)计算公式单位定义计算公式 常用单位定义长方 体 S 表=(长×宽+ 长×高+ 宽×高)×2S 表=(ab + ah + bh )×2 S 表=长×宽×2 + 长×高×2 +宽×高×2(上和下)(前和后) (左和右)S 表= 2ab + 2ah +2bh 逆运算:(长×宽+长×高+宽×高)×2=表面积x ×宽+x ×高+宽×高 =表面积÷2每相邻两个常用面积单位间进率为 100平方米 m 2平方分米 dm 2平方厘米cm 2V 长 = 长×宽×高 =abh V 长= 底面积×高 =Sh 或V 长=横截面积×长=Sa逆运算:① 设长XX ×宽×高 =长方体体积②长方体体积÷宽÷高=长 ③长方体体积÷底面积=高 体积单位,每相邻两个单位间进率为1000立方米m 3立方分米(升) 1dm 3=1L立方厘米(毫升)1cm 3=1mL体积容积(箱子、油桶、仓库、水池等)容器所能容纳物体的体积,通常叫做他们的容积。
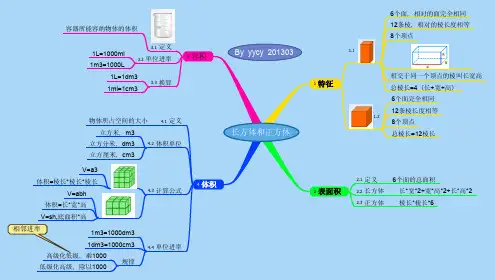
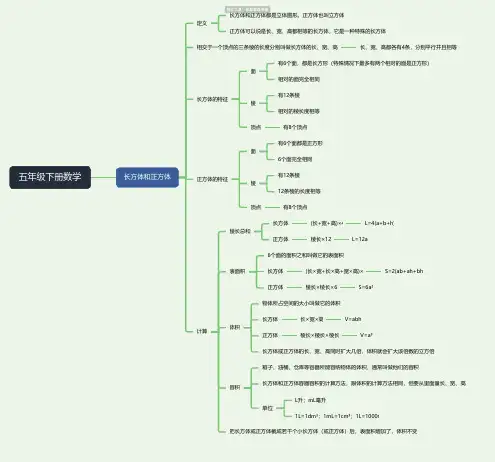
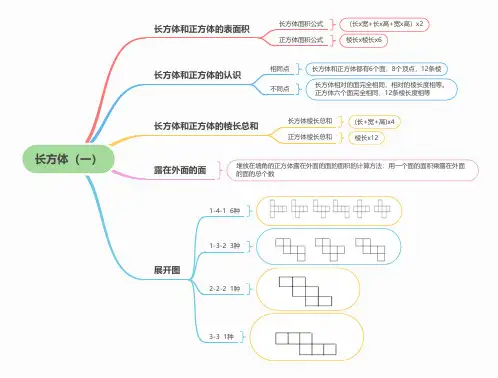
五年级下册数学长方体和正方体定义
长方体和正方体都是立体图形。
正方体也叫立方体
正方体可以说是长、宽、高都相等的长方体,它是一种特殊的长方体
相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高长、宽、高都各有4条,分别平行并且相等
长方体的特征
面
有6个面,都是长方形(特殊情况下最多有两个相对的面是正方形)
相对的面完全相同
棱
有12条棱
相对的棱长度相等
顶点有8个顶点
正方体的特征
面
有6个面都是正方形
6个面完全相同
棱
有12条棱
12条棱的长度相等
顶点有8个顶点
计算
棱长总和
长方体(长+宽+高)×4L=4(a+b+h)
正方体棱长×12L=12a
表面积
6个面的面积之和叫做它的表面积
长方体(长×宽+长×高+宽×高)×S=2(ab+ah+bh
正方体棱长×棱长×6S=6a²
体积
物体所占空间的大小叫做它的体积
长方体长×宽×高V=abh
正方体棱长×棱长×棱长V=a³
长方体或正方体的长、宽、高同时扩大几倍,体积就会扩大该倍数的立方倍容积
箱子、油桶、仓库等容器所能容纳物体的体积,通常叫做他们的容积
长方体和正方体容器容积的计算方法,跟体积的计算方法相同,但要从里面量长、宽、高
单位
L升;mL毫升
1L=1dm³;1mL=1cm³;1L=1000m
把长方体或正方体截成若干个小长方体(或正方体)后,表面积增加了,体积不变。

长方体和正方体知识梳理思维导图收集于网络,如有侵权请联系管理员删除100 叫做它的表面积。
长方体或正方体 个面的总面积,形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C长方体 =(长+宽+高)×4C 长方体 =4(a+b+h )逆运算:(方程法)设长X(X+宽+高)×4 = C 长X+宽+高 =棱长和÷4 (算术法)长=棱长和÷4-长-高正方体是长宽高都相等的特殊长方体。
6个12 条8 个有6个面,都是长方形。
(有时,最多有2个相对的面是正方形,其余4个面是完全相同的长方形)有3组棱(长、宽、高)每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
(上 下) (前 后)(左 右) 正 方 体6个12条8 个6个面都是 正方形。
12条棱长 度都相等。
6个面完全相同。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算:棱长和÷ 12 = 棱长正方体的棱长扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
形体S 表面积(6个面)V 体积(容积)计算公式单位定义计算公式常用单位定义长 方 体 S 表=(长×宽+ 长×高+ 宽×高)×2S 表=(ab + ah + bh )×2S表=长×宽×2 + 长×高×2 +宽×高×2(上和下)(前和后) (左和右)S表= 2ab + 2ah +2bh逆运算:(长×宽+长×高+宽×高)×2=表面每相邻两个常用面积单位间进率为 100平方米 m2V 长 = 长×宽×高 =abhV 长= 底面积×高 =Sh 或V 长=横截面积×长=Sa 逆运算:① 设长X X ×宽×高 =长方体体积 ②长方体体积÷宽÷高=长 体积单位,每相邻两个单位间进率为1000立方米m 3立方分米(升) 体积 容积(箱子、油桶、仓库、水池等)容器所能容纳物体的体积,通常叫做他们的容积。
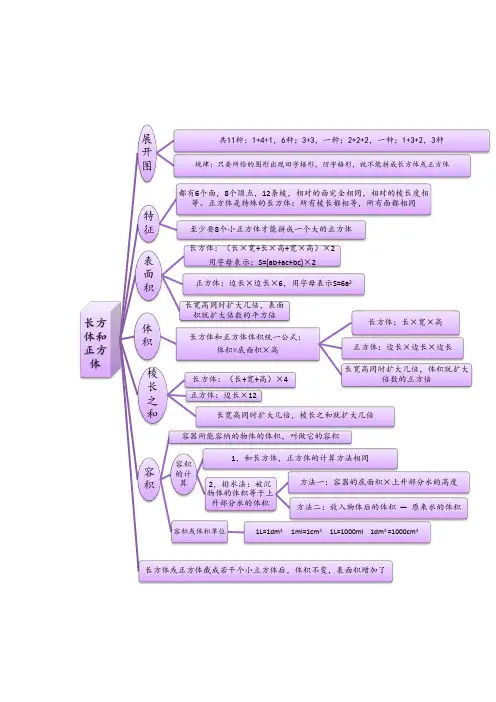
长方体和正方体展
开
图
共11种:1+4+1,6种;3+3,一种;2+2+2,一种;1+3+2,3种规律:只要所给的图形出现田字格形,凹字格形,就不能拼成长方体或正方体
特
征
都有6个面,8个顶点,12条棱,相对的面完全相同,相对的棱长度相
等。
正方体是特殊的长方体:所有棱长都相等,所有面都相同
至少要8个小正方体才能拼成一个大的正方体
表
面
积
长方体:(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ac+bc)×2
正方体:边长×边长×6,用字母表示S=6a2
长宽高同时扩大几倍,表面
积就扩大倍数的平方倍
体
积长方体和正方体体积统一公式:
体积=底面积×高
长方体:长×宽×高
正方体:边长×边长×边长
长宽高同时扩大几倍,体积就扩大
倍数的立方倍
棱
长
之
和
长方体:(长+宽+高)×4
正方体:边长×12
长宽高同时扩大几倍,棱长之和就扩大几倍
容
积
容器所能容纳的物体的体积,叫做它的容积
容积
的计
算
1,和长方体,正方体的计算方法相同
2,排水法:被沉
物体的体积等于上
升部分水的体积
方法一:容器的底面积×上升部分水的高度
方法二:放入物体后的体积—原来水的体积容积或体积单位1L=1dm3 1ml=1cm3 1L=1000ml 1dm3 =1000cm3
长方体或正方体截成若干个小立方体后,体积不变,表面积增加了。
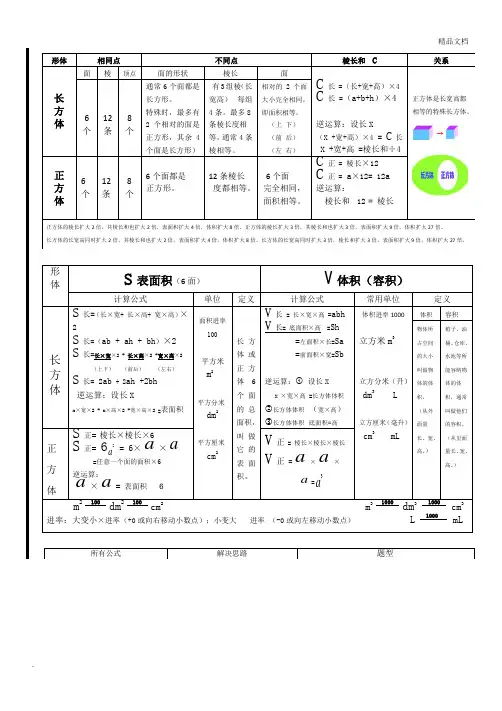
形体相同点不同点棱长和C关系长方体面棱顶点面的形状棱长面C长=(长+宽+高)×4C长 =(a+b+h)×4逆运算:设长X(X +宽+高)×4 = C长X +宽+高 =棱长和÷4正方体是长宽高都相等的特殊长方体。
6个12条8个通常6个面都是长方形。
特殊时,最多有2个相对的面是正方形,其余4个面是长方形)有3组棱(长宽高)每组4条。
最多8条棱长度相等,通常4条棱相等。
相对的2个面大小完全相同,即面积相等。
(上下)(前后)(左右)正方体6个12条8个6个面都是正方形。
12条棱长度都相等。
6个面完全相同,面积相等。
C正= 棱长×12C正=a×12= 12a逆运算:棱长和÷12 = 棱长正方体的棱长扩大2倍,其棱长和也扩大2倍,表面积扩大4倍,体积扩大8倍。
正方体的棱长扩大3倍,其棱长和也扩大3倍,表面积扩大9倍,体积扩大27倍。
长方体的长宽高同时扩大2倍,其棱长和也扩大2倍,表面积扩大4倍,体积扩大8倍。
长方体的长宽高同时扩大3倍,棱长和扩大3倍,表面积扩大9倍,体积扩大27倍。
形体S表面积(6面)V体积(容积)计算公式单位定义计算公式常用单位定义长方体S长=(长×宽+ 长×高+ 宽×高)×2S长=(ab + ah + bh)×2S长=长×宽×2 + 长×高×2 +宽×高×2(上下)(前后)(左右)S长= 2ab+ 2ah +2bh逆运算:设长Xx×宽×2 + x×高×2 +宽×高×2 =表面积面积进率100平方米m2平方分米dm2平方厘米cm2长方体或正方体6个面的总面积,叫做它的表面积。
V长= 长×宽×高=abhV长= 底面积×高 =Sh=左面积×长=Sa=前面积×宽=Sb逆运算:①设长XX ×宽×高 =长方体体积②长方体体积÷(宽×高)③长方体体积÷底面积=高体积进率1000立方米m3立方分米(升)dm3 L立方厘米(毫升)cm3 mL体积容积物体所占空间的大小叫做物体的体积。
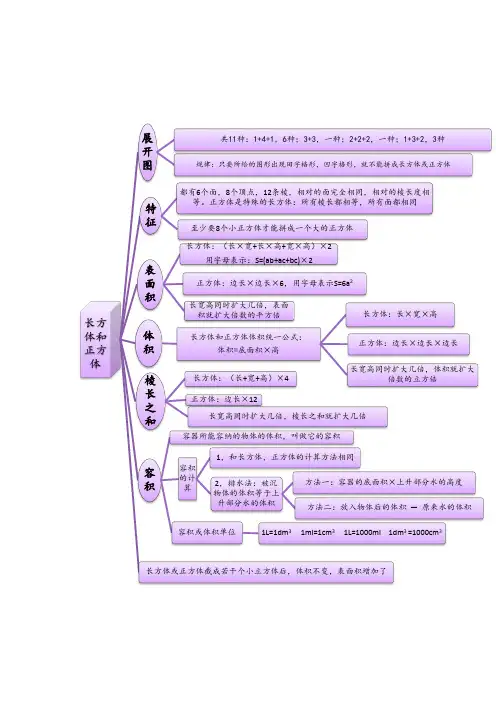
长方体和正方体展
开
图
共11种:1+4+1,6种;3+3,一种;2+2+2,一种;1+3+2,3种
规律:只要所给的图形出现田字格形,凹字格形,就不能拼成长方体或正方体
特
征
都有6个面,8个顶点,12条棱,相对的面完全相同,相对的棱长度相
等。
正方体是特殊的长方体:所有棱长都相等,所有面都相同
至少要8个小正方体才能拼成一个大的正方体
表
面
积
长方体:(长×宽+长×高+宽×高)×2
用字母表示:S=(ab+ac+bc)×2
正方体:边长×边长×6,用字母表示S=6a2
长宽高同时扩大几倍,表面
积就扩大倍数的平方倍
体
积
长方体和正方体体积统一公式:
体积=底面积×高
长方体:长×宽×高
正方体:边长×边长×边长
长宽高同时扩大几倍,体积就扩大
倍数的立方倍
棱
长
之
和
长方体:(长+宽+高)×4
正方体:边长×12
长宽高同时扩大几倍,棱长之和就扩大几倍
容
积
容器所能容纳的物体的体积,叫做它的容积
容积
的计
算
1,和长方体,正方体的计算方法相同
2,排水法:被沉
物体的体积等于上
升部分水的体积
方法一:容器的底面积×上升部分水的高度
方法二:放入物体后的体积—原来水的体积容积或体积单位1L=1dm3 1ml=1cm3 1L=1000ml 1dm3 =1000cm3
长方体或正方体截成若干个小立方体后,体积不变,表面积增加了。
叫做它的表面积。
长方体或正方体6个面的总面积,形体 相同点 不同点棱长和 C关系长 方 体面棱顶点面的形状 棱长 面C 长方体 =(长+宽+高)×4C 长方体 =(a+b+h )×4逆运算:(方程法)设长X(X +宽+高)×4 = C 长X +宽+高 =棱长和÷4 (算术法)长=棱长和÷4-长-宽正方体是长宽高都相等的特殊长方体。
6个12 条8 个有6个面都是长方形。
有时,最多有2个相对的面是正方形,其余4个面是完全相同的长方形)有3组棱(长宽高)每组4条。
相对的4条棱相等。
最多8条棱长度相等。
相对的2个面完全相同。
(上 下)(前 后)(左 右) 正 方 体6个12条8 个6个面都是 正方形。
12条棱长度都相等。
6个面完全相同, 面积相等。
C 正 = 棱长×12 C 正 = a ×12= 12a逆运算:棱长和÷ 12 = 棱长正方体的棱长扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
长方体的长、宽、高同时扩大n 倍,其棱长和也扩大n 倍;表面积扩大n 2倍;体积扩大n 3倍。
形体S 表面积(6面)V 体积(容积)计算公式单位定义计算公式常用单位定义长 方 体 S 表=(长×宽+ 长×高+ 宽×高)×2S 表=(ab + ah + bh )×2S表=长×宽×2 + 长×高×2 +宽×高×2(上和下)(前和后) (左和右)S表= 2ab + 2ah +2bh逆运算:设长X(x ×宽+x ×高+宽×高)×2=表面积x ×宽+x ×高+宽×高 =表面积÷2面积每相邻单位间进率为 100平方米m 2 平方分米dm2V 长 = 长×宽×高 =abhV 长= 底面积×高 =Sh (=左面积×长=Sa =前面积×宽=Sb ) 逆运算:① 设长X X ×宽×高 =长方体体积 ②长方体体积÷(宽×高) ③长方体体积÷底面积=高体积进率1000 立方米m 3立方分米(升)1dm 3=1L体积 容积箱子、油桶、仓库、水池等所能容纳物体的体积,通常叫做他们的容积。