1-5 无穷小与无穷大的性质
- 格式:ppt
- 大小:1.40 MB
- 文档页数:20




无穷小与无穷大无穷小和无穷大是数学中重要的概念,它们在极限运算和微积分中有着重要的作用。
本文将介绍无穷小和无穷大的定义、性质以及它们在数学和物理中的应用。
一、无穷小的定义与性质无穷小是指函数在某一点附近取值时,其值趋近于零的特殊情况。
具体说,对于函数f(x),如果当x无限接近某一点a时,f(x)也无限接近于零,那么f(x)就是在点a处的无穷小。
常表示为lim x→a f(x) = 0。
1.1 阶与比较无穷小可以根据其趋近于零的速度分为不同的阶。
例如,当x无限接近零时,x^2相比于x,其趋近于零的速度更快,因此x^2是x的高阶无穷小。
同样,x^n(n>1)相比于x,其趋近于零的速度更快,因此x^n是x的高阶无穷小。
1.2 运算性质无穷小具有一些运算性质。
例如,两个无穷小的和仍然是无穷小,若f(x)为无穷小,g(x)为有界函数,则f(x)g(x)为无穷小。
此外,无穷小与有界函数的乘积也为无穷小。
1.3 等价无穷小在无穷小的研究中,等价无穷小也是一个重要的概念。
如果两个无穷小f(x)和g(x)满足li m x→a (f(x)/g(x)) = 1,那么称f(x)和g(x)是在点a处等价的无穷小。
等价无穷小具有相似的性质,在一些极限运算中可以互相替换。
二、无穷大的定义与性质无穷大是指函数在某一点附近取值时,其值趋近于正无穷或负无穷的情况。
具体说,对于函数f(x),如果当x趋近于某一点a时,f(x)的值无限增大或无限减小,那么f(x)就是在点a处的无穷大。
2.1 正无穷和负无穷无穷大可以分为正无穷大和负无穷大。
当x趋近于某一点a时,若f(x)的值无限增大,则称f(x)为正无穷大。
若f(x)的值无限减小,则称f(x)为负无穷大。
2.2 无穷大的性质无穷大具有一些基本性质。
例如,正无穷大与负无穷大的和仍然是无穷大。
另外,无穷大与常数的乘积仍然是无穷大。
然而,无穷大的乘积与除法需要谨慎处理。
2.3 无穷大与极限在求解极限问题时,无穷大也扮演了重要的角色。



无穷小量与无穷大量无穷小量和无穷大量是微积分中重要的概念之一。
它们在极限理论的研究中起着重要的作用,能够描述数列、函数等的趋势和极限。
本文将从无穷小量和无穷大量的定义、性质以及在微积分中的应用等方面进行介绍和探讨。
一、无穷小量的定义和性质无穷小量是指当自变量趋于某个值时,函数值趋于零的量。
通常用符号"ε"或者"δ"表示。
具体而言,如果对于任意给定的正数ε,存在另一个正数δ,使得当自变量趋于某个值x时,函数值满足0<|f(x)|<ε,那么函数f(x)就是无穷小量。
无穷小量具有以下的性质:1. 无穷小量的高阶无穷小量比低阶无穷小量高阶,也就是说,当x趋于某个值时,x的幂次越高的无穷小量趋于零的速度越快。
2. 无穷小量可以进行四则运算,即两个无穷小量的和、差、积仍然是无穷小量。
3. 无穷小量与有界函数的乘积还是无穷小量。
4. 无穷小量与无穷小量的乘积还是无穷小量。
这些性质使得无穷小量在微积分的运算中具有重要的意义,可以方便地进行极限的计算和推导。
二、无穷大量的定义和性质无穷大量是指当自变量趋于某个值时,函数值趋于无穷的量。
通常用符号"∞"表示。
具体而言,如果对于任意给定的正数M,存在另一个正数δ,使得当自变量趋于某个值x时,函数值满足f(x)>M,那么函数f(x)就是无穷大量。
无穷大量具有以下的性质:1. 无穷大量的相反数是无穷小量。
2. 无穷大量与有界函数的乘积可以是无穷大量或者无穷小量,具体取决于有界函数的性质。
3. 无穷大量与无穷大量的四则运算结果不确定,可能是无穷大量、无穷小量或者有限量,具体取决于无穷大量的相对大小关系。
无穷大量在极限的计算和研究中起着重要的作用,可以帮助我们判断函数的趋势和性质,解决一些特殊的极限问题。
三、无穷小量与极限的关系无穷小量是极限的重要概念,它与极限之间存在着密切的关系。
当我们讨论函数在某一点的极限时,实际上就是在讨论自变量趋于某一点时,函数值的趋势。


无穷小与无穷大的概念无穷小与无穷大是数学中常用的概念,它们在微积分和极限理论中起着至关重要的作用。
本文将介绍无穷小与无穷大的定义、性质及其在数学和物理问题中的应用。
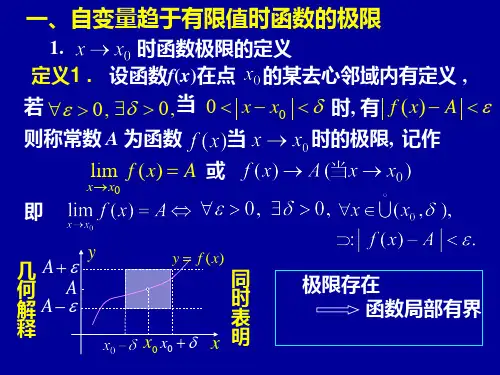
一、无穷小的定义与性质在数学中,无穷小是指当自变量趋向某个特定的值时,其取值趋近于零的量。
通常用符号"ε" 或"δ" 表示无穷小。
具体而言,对于任意一个正数ε,如果函数 f(x) 满足对于任意足够小的 x,有|f(x)|<ε 成立,则称 f(x) 为无穷小。
无穷小可以是正无穷小、负无穷小或零无穷小。
在运算中,无穷小具有以下性质:1. 有界性:无穷小是一种无界量,但是无穷小的和、差和积仍然是无穷小。
2. 消去性:与有界量相乘或相加的无穷小最终可以忽略不计。
二、无穷大的定义与性质无穷大是指当自变量趋向某个特定的值时,函数的取值趋近于无穷大的量。
通常用符号"∞" 表示无穷大。
具体而言,对于任意一个正数M,如果函数 f(x) 满足对于任意足够大的 x,有 |f(x)|>M 成立,则称f(x) 为无穷大。
在运算中,无穷大具有以下性质:1. 增长性:无穷大可以比任何有界量更大。
2. 加法性:无穷大与有界量相加或相减,最终仍然是无穷大。
3. 乘法性:无穷大与正无穷大或负无穷大相乘,结果为正无穷大或负无穷大。
三、无穷小和无穷大的应用1. 极限计算:无穷小和无穷大在极限计算中经常使用。
通过使用无穷小和无穷大的性质,可以简化复杂的极限计算过程。
2. 函数分析:无穷小和无穷大也用于函数的分析与研究中。
通过判断函数在不同自变量取值情况下的无穷小和无穷大的行为,可以推断函数的性质和特点。
3. 物理应用:无穷小和无穷大在物理学中也有广泛的应用。
例如,在物体运动的瞬间,可以把时间看作无穷小,从而简化物体的运动方程。
4. 工程应用:无穷小和无穷大在工程学中也有实际应用。
例如,在电路分析中,可以使用无穷大来近似分析电路的特性。