当前位置：文档之家 › 2015届高考数学总复习第十章 第二节直线与圆的位置关系精讲课件 文

2015届高考数学总复习第十章 第二节直线与圆的位置关系精讲课件 文

  • 格式：ppt
  • 大小：1.17 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

4.2.1《直线与圆的位置关系》PPT课件

4.2.1《直线与圆的位置关系》PPT课件

巩固练习：
①判断直线４x－３y=50与圆 x 2 y 2 100的位置关系．如
果相交，求出交点坐标．
解：因为圆心O（0，0）到直线４x－３y=50
| 0 0 50 |
的距离d=
5
= 10
而圆的半径长是10，所以直线与圆相切。 圆心与切点连线所得直线的方程为3x+4y=0
解方程组
4x 3x
3 4
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人：XXXXXX 时 间：XX年XX月XX日
A2 B2
直线与圆的位置关系
在2009年08月08日台凤莫拉克袭击宝岛台湾时，
一艘轮船在沿直线返回泉州港口的途中，接到气象台
的台风预报：台风中心位于轮船正西70km处，受影响
的范围是半径长为30km的圆形区域．已知泉州港口位
于台风中心正北40km处，如果这艘轮船不改变航线，
那么它是否会受到台风莫拉克的影响？ y
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
谢谢你的到来
学习并没有结束，希望大家继续努力
为解决这个问题，我们以台
港口
风中心为原点 O，东西方向为
x 轴，建立如图所示的直角坐 标系，其中取 10km 为单位长
O
轮船 x
度．
直线与圆的位置关系
这样，受台风影响的圆区域所对应的圆心为O的圆

高考数学复习课件 8.3 直线 圆的位置关系 理 新人教版

高考数学复习课件 8.3 直线 圆的位置关系 理 新人教版

D．3
解析：设 P(x0，y0)为直线 y＝x＋1 上一点，圆心 C(3,0)
到 P 点的距离为 d，切线长为 l，则 l＝ d2－1，当 d 最小
时 l 最小，
又 PC 垂直于直线 y＝x＋1 时，d 最小，此时 d＝2 2，
所以 lmin＝ 2 22－1＝ 7. 答案：C
4．若曲线C1：x2＋y2－2x＝0与曲线C2：y(y－mx－m)
在解决直线与圆的位置关系的问题时，一定要联系 圆的几何性质，利用有关图形的几何特征，尽可能简化 运算，讨论直线与圆的位置关系时，一般不用Δ＞0、 Δ＝0、Δ＜0，而用圆心到直线距离d＜r、d＝r、d＞r分 别确定相交、相切、相离的位置关系．
(1)涉及圆的切线时，要考虑过切点与切线垂直的 半径，计算弦长时，要用半径、弦心距、弦长的一半构
1．过点P(0,1)与圆x2＋y2－2x－3＝0相交的所有直线
中，被圆截得的弦最长时的直线方程是
()
A．x＝0
B．y＝1
C．x＋y－1＝0
D．x－y＋1＝0
解析：(x－1)2＋y2＝4，圆心为(1,0)，由题意知直线过
圆心，所以直线方程为1x＋1y＝1，即 x＋y－1＝0. 答案：C
2．将圆x2＋y2＝1沿x轴正方向平移1个单位后得圆C， 若过点(3,0)的直线l和圆C相切，则直线l的斜率为 ( )
A.
3 3
B.
33或－
3 3
C. 3
D. 3或Leabharlann 3关键提示：利用数形结合判断知 OM 为圆的切线，则xy
即为切线的斜率．
解析：因为O→M·C→M＝0， 所以 OM⊥CM，所以 OM 是圆的切线． 设 OM 的方程为 y＝kx， 由 k|22k＋| 1＝ 3得 k＝± 3，即xy＝± 3. 答案：D

2015年高考数学(文)一轮课件：10-4直线与圆、圆与圆的位置关系

2015年高考数学(文)一轮课件：10-4直线与圆、圆与圆的位置关系

解析：如图，取 AB 中点 C，连接 OC、OA，则 OC⊥AB，|OA| |0－2×0＋5| ＝2 2，|OC|＝ 2 2 ＝ 5， 1 ＋－2 ∴|AC|＝ 8－5＝ 3，
∴|AB|＝2|AC|＝2 3.
答案：2 3
核心考点
引领通关
考点研析 变式通关
考点一
直线与圆的位置关系
【例 1】 已知直线 l：y＝kx＋1，圆 C：(x－1)2＋(y＋1)2＝12. (1)试证明：不论 k 为何实数，直线 l 和圆 C 总有两个交点； (2)求直线 l 被圆 C 截得的最短弦长． 思维启迪：直线与圆的交点个数即为直线方程与圆方程联立而 成的方程组解的个数；最短弦长可用代数法或几何法判定．
m∈ －
3 3 ， ，又当 m＝0 时，直线 l 与 x 轴重合，此时只 3 3
有两个交点，应舍去．故选 B.
答案：B
考点二
圆与圆的位置关系
【例 2】 a 为何值时，圆 C1：x2＋y2－2ax＋4y＋a2－5＝0 和 圆 C2：x2＋y2＋2x－2ay＋a2－3＝0. (1)外切；(2)相交；(3)外离；(4)内切． 思维启迪：(1)分别表示出两圆的圆心坐标和半径；(2)利用圆心 距与两圆半径的关系求解．
4．圆与圆的位置关系的判定 设⊙C1：(x－a1)2＋(y－b1)2＝r2 1(r1＞0)， ⊙C2：(x－a2)2＋(y－b2)2＝r2 2(r2＞0)，则有 8 ____； |C1C2|＞r1＋r2⇔⊙C1 与⊙C2□ 9 ____； |C1C2|＝r1＋r2⇔⊙C1 与⊙C2□
10 ____； |r1－r2|＜|C1C2|＜r1＋r2⇔⊙C1 与⊙C2□ 11 ____； |C1C2|＝|r1－r2|(r1≠r2)⇔⊙C1 与⊙C2□ 12 ____. |C1C2|＜|r1－r2|⇔⊙C1 与⊙C2□

2015高考数学(理)一轮复习考点突破课件：8.4直线与圆、圆与圆的位置关系

2015高考数学(理)一轮复习考点突破课件：8.4直线与圆、圆与圆的位置关系

题型一 直线与圆的位置关系
• • (1)过点P(2,4)引圆(x－1)2＋(y－1)2＝1的切线，则切线方 程为________； (2)若经过点A(4,0)的直线l与圆(x－2)2＋y2＝1有公共点，则直线 l的斜率的取值范围为________．
【解析】
(1)当直线的斜率不存在时，直线方程为 x＝2，此时，
(2)(2013· 湖北)已知圆 O：x2＋y2＝5，直线 l1：xcos θ＋ysin θ＝
π 10＜θ＜2.设圆
O 上到直线 l 的距离等于 1 的点的个数为 k，
则 k＝________.
解析：(1)圆的标准方程为(x－1)2＋(y－2)2＝5，则圆心(1,2)到直线 |1＋4－5＋ 5| x＋2y－5＋ 5＝0 的距离 d＝ ＝1，∴直线 x＋2y－5 5 ＋ 5＝0 被圆 x2＋y2－2x－4y＝0 截得的弦长为 2 52－12＝4. 选 C.
• • • • • • • •
2．圆与圆的位置关系的判定 设⊙C1：(x－a1)2＋(y－b1)2＝r(r1＞0)， ⊙C2：(x－a2)2＋(y－b2)2＝r(r2＞0)，则有： |C1C2|＞r1＋r2⇔⊙C1与⊙C2外离； |C1C2|＝r1＋r2⇔⊙C1与⊙C2外切； |r1－r2|＜|C1C2|＜r1＋r2⇔⊙C1与⊙C2相交； |C1C2|＝|r1－r2|(r1≠r2)⇔⊙C1与⊙C2内切． |C1C2|＜|r1－r2|⇔⊙C1与⊙C2内含．
• •
1．直线与圆的位置关系 位置关系有三种： 、
相交
、
相切
相离
．
判断直线与圆的位置关系常见的有两种方法： Δ＞0⇔ 相交 ； 判别式 (1)代数法： ― ― ― ― ― ― ― → Δ＝0⇔ 相切 ； 2― Δ＝b －4ac Δ＜0⇔ 相离 . (2)几何法：利用圆心到直线的距离 d 和圆半径 r 的大小关系：d ＜r⇔ 相交 ，d＝r⇔ 相切 ，d＞r⇔ 相离 ．

高考数学一轮复习 4-1.2直线与圆的位置关系精品课件 新人教版

高考数学一轮复习 4-1.2直线与圆的位置关系精品课件 新人教版
第二讲 直线与圆的位置关系
回归课本
直线与圆的位置关系
1.圆周角定理:圆上一条弧所对的圆周角等于它所对的圆心角的一半.
圆心角定理:圆心角的度数等于它所对弧的度数. 推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧 相等. 推论2:半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径. 弦切角定理:弦切角等于它所夹的弧所对的圆周角.
【典例1】 如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交 于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
(1)证明:A,P,O,M四点共圆;
(2)求∠OAM+∠APM的大小. [分析] 要证A､P､O､M四点共圆,可考虑四边形APOM的对角互补;根据四点 共圆,同弧所对的圆周角相等,进行等量代换,进而求出∠OAM+∠APM的大小.
在 APD中, AD 2 PA 2 PD 2 2PA PD 2 3 cosAPD 6b 9b 2 b 3b cosAPD 2
2 2
15b 2 6 6cosAPD. 5 2 b 6b 2 cosAPD 2 BC 1 2 , 2 2 2 AD 15b 6 6b cosAPD 6 BC 6 . AD 6 6 答案 : 6
2.圆内接四边形的性质定理与判定定理:
圆内接四边形的对角互补;圆内接四边形的外角等于它的内角的对角.
如果一个四边形的对角互补,那么这个四边形的四个顶点共圆;如果四边形 的一个外角等于它的内角的对角,那么这个四边形的四个顶点共圆.
3.切线的性质定理:圆的切线垂直于经过切点的半径.
推论:经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的
解析:连接OA,OB, ∵∠BCA=45°,∴∠AOB=90°. 设圆O的半径为R,在Rt△AOB中,R2+R2=AB2=16,∴R2=8. ∴圆O的面积为8π. 答案:8π

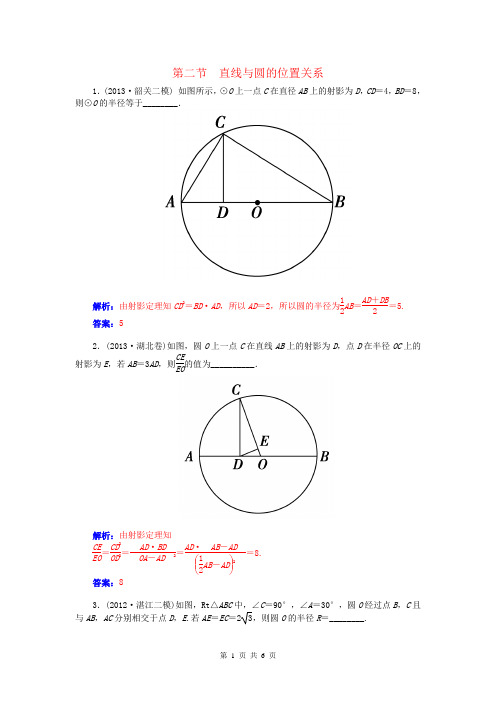
2015届高考数学总复习 第十章 第二节直线与圆的位置关系课时精练试题 文(含解析)

2015届高考数学总复习 第十章 第二节直线与圆的位置关系课时精练试题 文(含解析)

第二节 直线与圆的位置关系1．(2013·韶关二模) 如图所示，⊙O 上一点C 在直径AB 上的射影为D ，CD ＝4，BD ＝8，则⊙O 的半径等于________．解析：由射影定理知CD 2＝BD ·AD ，所以AD ＝2，所以圆的半径为12AB ＝AD ＋DB 2＝5.答案：52．(2013·湖北卷)如图，圆O 上一点C 在直线AB 上的射影为D ，点D 在半径OC 上的射影为E ，若AB ＝3AD ，则CE EO的值为__________．解析：由射影定理知 CE EO ＝CD 2OD 2＝AD ·BD OA －AD 2＝AD AB －AD ⎝ ⎛⎭⎪⎫12AB －AD 2＝8. 答案：83．(2012·湛江二模)如图，Rt△ABC 中，∠C ＝90°，∠A ＝30°，圆O 经过点B ，C 且与AB ，AC 分别相交于点D ，E .若AE ＝EC ＝23，则圆O 的半径R ＝________.解析：连接BE ，因为∠C ＝90°，所以BE 为圆O 的直径．因为∠A ＝30°，AC ＝43，所以BC ＝4.在Rt△BCE 中，由勾股定理得BE ＝27，所以圆O 的半径R ＝7.答案：74．(2013·广州三校广一模后适应性训练)如图，半径为2的⊙O 中，∠AOB ＝90°，D 为OB 的中点，AD 的延长线交⊙O 于点E ，则线段DE 的长为__________．解析：在Rt△AOD 中，AO ＝2，DO ＝1，所以AD ＝22＋12＝5，又BD ＝1，由相交弦定理得AD ·DE ＝3DO ·BD ，即5DE ＝3×1，所以DE ＝355.答案：3555．如图，点A 、B 、C 是圆O 上的点，且AB ＝2，BC ＝6，∠CAB ＝2π3，则∠AOB 对应的劣弧长为__________．解析：连接CO ，因为∠CAB ＝2π3，所以AB 优弧所对的圆心角为4π3，从而∠BOC ＝2π3，在等腰三角形BOC 中可求得半径OB ＝2，因为AB ＝2，所以△AOB 为等腰直角三角形，所以∠AOB 对应的劣弧长为2π2.答案：2π26．(2012·韶关模拟)如图，AB 是圆O 的直径，AD ＝DE ，AB ＝8， BD ＝6，则AD AC＝________.解析：因为AD ＝DE ，所以∠ABD ＝∠DAE .又∠ADC 为公共角，所以△ADC ∽△BDA .所以AD AC＝BD AB ＝68＝34. 答案：347．(2012·深圳调研)如图所示，AB 是圆O 的直径，弦AD 和BC 相交于点P ，连接CD .若∠APB ＝120°，则CD AB等于________．解析：连接AC ，依题意∠APC ＝60°，因为AB 是圆O 的直径，所以∠ACP ＝90°.所以cos ∠APC ＝PC PA ＝12.又△PAB ∽△PDC ，所以CD AB ＝PC PA ＝12.答案：128．(2013·揭阳二模)如图，C 、D 是半圆周上的两个三等分点，直径AB ＝4，CE ⊥AB ，垂足为E ，与BD 相交于点F ，则BF 的长为__________．解析：依题意知∠DBA ＝30°，则AD ＝2，过点D 作DG ⊥AB 于G ，则AG ＝BE ＝1，所以BF ＝BE cos 30°＝233.答案：2339．(2012·陕西卷)如图所示，在圆O 中，直径AB 与弦CD 垂直，垂足为E ，EF ⊥DB ，垂足为F ，若AB ＝6，AE ＝1，则DF ·DB ＝________.解析：连接AD .在Rt△ABD 中，DE ⊥AB ，所以DE 2＝AE ·EB ＝5.在Rt△EBD 中，EF ⊥DB ，所以DE 2＝DF ·DB ＝5.答案：510．如图，PA 切圆O 于点A ，割线PBC 经过O ，OB ＝PB ＝1，OA 绕着点O 逆时针旋转60°到OD ，PD 交圆O 于点E 则PE 的长为________．答案：37711．(2013·陕西卷)如图，弦AB 与CD 相交于⊙O 内一点E ，过E 作BC 的平行线与AD 的延长线相交于点P .已知PD ＝2DA ＝2, 则PE ＝__________.解析：因为BC ∥PE ，所以∠BCD ＝∠PED ，且在圆中，由∠BCD ＝∠BAD 得∠PED ＝∠BAD ，所以△EPD ∽△APE ，于是PE PA ＝PDPE， 得PE 2＝PA ·PD ＝3×2＝6，所以PE ＝ 6.答案： 612．(2012·天津卷)如图所示，已知AB 和AC 是圆的两条弦，过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ，与AB 相交于点F ，AF ＝3，FB＝1，EF ＝32，则线段CD 的长为________．解析：由相交弦的性质可得AF ·FB ＝EF ·FC ，∴FC ＝AF ·FB EF ＝3×132＝2.又∵FC ∥BD ，∴AC AD ＝FC BD ＝AF AB ＝34，即BD ＝83.由切割定理得BD 2＝DA ·DC ＝4DC 2，解得DC ＝43.答案：4313．(2013·陕西咸阳二模)如图，A 、B 是两圆的交点，AC 是小圆的直径，D 、E 分别是CA 、CB 的延长线与大圆的交点，已知AC ＝4，BE ＝10，且BC ＝AD ，则AB ＝______________.解析：设BC ＝AD ＝x ，则由切割线定理得， CA ·CD ＝CB ·CE ，即4(4＋x )＝x (x ＋10)，解得x ＝2，即CB ＝2，又AC 是小圆的直径，所以AB ＝CA 2－CB 2＝42－22＝2 3. 答案：2 314．(2012·辽宁卷)如图所示，⊙O 和⊙O ′相交于A ，B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连接DB 并延长交⊙O 于点E .证明：(1)AC ·BD ＝AD ·AB ； (2)AC ＝AE .证明：(1)由AC 与⊙O ′相切于A ，得∠CAB ＝∠ADB ， 同理∠ACB ＝∠DAB ， 所以△ACB ∽△DAB .从而AC AD ＝ABBD，即AC ·BD ＝AD ·AB .(2)由AD 与⊙O 相切于A ，得∠AED ＝∠BAD . 又∠ADE ＝∠BDA ，得△EAD ∽△ABD .从而AE AB ＝ADBD，即AE ·BD ＝AD ·AB .结合(1)的结论，得AC ＝AE .。

高中数学人教A版必修第二节直线与圆的位置关系课件


高中数学人教A版必修2第四章第二节 直线与 圆的位 置关系 课件(共17张PPT)
高中数学人教A版必修2第四章第二节 直线与 圆的位 置关系 课件(共17张PPT)
例1 如图，已知直线l： 3x y 6 和0 圆心为C的 圆 x2 y2 2y 4 0 ，判断直线 l 与圆的位置关系；
直线与圆有无公共点？
解法一：由直线 l 与圆的方程Fra bibliotek得：消去y，得：
3x y 6 0, x2 y2 2y 4 0. x2 3x 2 0
因为： (3)2 4 1 2
=1>0 直线 l 与圆相交，有两个公共点．
A（2，0），B（1，3）
高中数学人教A版必修2第四章第二节 直线与 圆的位 置关系 课件(共17张PPT)
总结： 判定直线 与圆的位置关系的方法有_两___种：
（1）根据定义，由___直__线____与___圆___的_ 公共点 的个数来判断；
（2）根据性质，由_圆__心__到___直__线__的__距___离d与半径r 的关系来判断。
在实际应用中，常采用第二种方法判定。
高中数学人教A版必修2第四章第二节 直线与 圆的位 置关系 课件(共17张PPT)
直线与圆的位置关系判断方法：
二、几何方法。主要步骤：
把直线方程化为一般式,利用圆方程求出圆心和半径
利用点到直线的距离公式求圆心到直线的距离
作判断: 当d>r时，直线与圆相离；当d=r时，直线与 圆相切;当d<r时，直线与圆相交
高中数学人教A版必修2第四章第二节 直线与 圆的位 置关系 课件(共17张PPT)
3)若d= 8 cm ,则直线与圆_相__离___, 直线与圆有__0__个公共点.

2.5直线与圆的位置关系内切圆课件

A
2 1
I
3
B
4 5
D
E
C
练习：
1、如图，已知 ABC内心为O,且 BOC=110, 40°. 则 A=
2、已知三角形ABC的外心为O，且∠BOC=110°则 55或125 ∠A=____ __度。 3、三角形ABC中， ∠A= 50°,I是三角形的内心， 115° O是三角形的外心，则∠ BIC=______ ∠ BOC=________ 100°
思考:我们所学的平行四边形，矩形，菱形，正方 形，等腰梯形中，哪些四边形一定有内切圆？
(菱形，正方形一定有内切圆)
2.5 直线与圆的位置关系（3）
例1
典型例题
如图，⊙O是△ABC的内切圆，切点分别为D
E、F，∠B＝60°，∠C＝70°，
求∠EDF的度数． 拓展：∠A与∠EDF有什么关系？
变式：若G点是圆上任意点（不与E,F重合）求∠EGF度数 变式：连接BO,CO,求∠BOC度数 变式：（1）若∠A=80 °,则∠BOC= （2）若∠BOC=100 °，则∠A= 度。 度。
试探讨∠BOC与∠A之间存在怎样的数量关系？ 请说明理由．
变式：如图，从⊙O外一点P作⊙O的两条切 线，分别切⊙O于A，B，在AB 上任取一点C 作⊙O的切线分别交PA、PB于D、E
连结OD，OE，若∠P=400，则∠DOE=_____; 若∠P=n° ,则∠DOE=_______ 连结OA，OB，若∠P=400，则∠AOB=_____; D P C E
D
C
三角形内切圆的圆心叫三角形的内心
①三角形的内心是三角形角平分线的交点 ②三角形的内心到三边的距离相等 ③三角形的内心一定在三角形的内部
三角形内心的性质

9.5 直线与圆的位置关系


d < r ⇔ 相交 d = r ⇔ 相切 d > r ⇔ 相离
一般宜用几何法。
(1)过定点P(x0,y0)的圆的切线： ①点P(x0,y0)在圆上：则圆x2+y2=r2的切线方程为 x0x+y0y=r2； 圆x2+y2+Dx+Ey+F=0的切线方程为 x + x0 y0 + y x0x+y0y+D +E ·+F=0. 2 2
24 ， 7
高考总复习·数学 高考总复习 数学
(2)连结CP、CQ，则CP⊥PM，CQ⊥QM. ∴M、P、Q、C四点共圆. 其圆是以CM为直径的圆. ∵C(1,-3),∴CM的中点为( |CM|=
3 2
2
1 , 2
=5.
).
(2 − 1) + (4 + 3)
2
2
高考总复习·数学 高考总复习 数学
1 2 25 ∴以CM为直径的圆的方程为(x ) =. 2 2 1 3 2 25 2+(y+3)2-1-［(x2∴PQ的方程为(x-1) ) +(y) ］ 2 2 2
3 2
)2+(y
=0，即
x+7y+19=0.
高考总复习·数学 高考总复习 数学 求圆的圆心坐标、 求圆的圆心坐标、半径和方程等
已知圆x2+y2+x-6y+m=0与直线x+2y-3=0相交于 P,Q两点，O为原点，且OP⊥OQ，求该圆的圆心坐标及 半径。 思路分析： 思路分析： 由于OP⊥OQ，所以kOP·kOQ=－1，问题可解.
高考总复习·数学 高考总复习 数学 （２）弦长最小值时，l ⊥ＡＣ ， 由kAC= - 1/2, 所以的方 程为2x-y-5=0. 【点评与感悟】用直线系方程求点。若证明一条直线恒 点评与感悟】 过定点或求一条直线必过定点，通常采用分离系数法： 即将原方程改变成：f(x, y)+mg(x,y)=0的形式，此式的 成立与m的取值无关，从而解出定点。

2015年湖南师大附中高一数学必修二全套课件：4.2.1直线与圆的位置关系【湘教版】


2.利用点到直线的距离公式求圆心 到直线的距离d；
3.比较d与r的大小关系：
若d＞r，则直线与圆相离； 若d＝r，则直线与圆相切； 若d＜r，则直线与圆相交．
知识探究（二）：圆的切线方程
思考1:过圆上一点、圆外一点作圆 的切线，分别可作多少条？
M
M
思考2:设点M(x0，y0)为圆x2＋y2=r2 上一点，如何求过点M的圆的切线方 程？
4．2 4.2.1
直线、圆的位置关系 直线与圆的位置关系
问题提出
1 5730 p 2
t
1、点到直线的距离公式， 圆的 标准方程和一般方程分别是什么？
d | Ax0 By0 C | A B
2 2
( x a) ( y b) r
2 2
2 2
2
x y Dx Ey F 0( D E 4F 0)
思考1:在平面几何中，直线与圆的 位置关系有几种？
思考2:在平面几何中，我们怎样判 断直线与圆的位置关系？
d r d r r
d
d <r
D =r
d >r
思考3:如何根据直线与圆的公共点 个数判断直线与圆的位置关系？
两个公共点
一个公共点
没有公共点
思考4:在平面直角坐标系中，我们 用方程表示直线和圆，如何根据直 线与圆的方程判断它们之间的位置 关系？ 方法一:根据直线与圆的联立方程组 的公共解个数判断； 方法二:根据圆心到直线的距离与圆 半径的大小关系判断.
y
M
o x
x0x+y0y=r2
思考3:设点M(x0，y0)为圆 x2＋y2=r2 外一点，如何求过点M的圆的切线方 程？
y
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

点评：圆内接四边形的问题主要有判断四点共圆或判断四边 形为圆内接四边形等，对角互补是四边形为圆内接四边形的 充要条件. 判断“四点共圆”的方法还有四边形的外角和内对 角相等，以及同弧的圆周角相等等 . 解题时首先尝试有没有 “四点共圆”，然后再找角的关系．
变式探究 4 ． (2012· 深圳松岗中学模拟 ) 如图，在
变式探究 3．(2012· 湖南卷)如图所示，过点P的直线与⊙O相交于A，B 两 点 ． 若 PA ＝ 1 ， AB ＝ 2 ， PO ＝ 3 ， 则 ⊙ O 的 半 径 等 于 ________．
解析：利用割线定理求解． 设⊙O 的半径为 r(r＞0)，∵PA＝1，AB＝2，∴PB＝PA＋AB ＝3，延长 PO 交⊙O 于点 C，则 PC＝PO＋r＝3＋r. 设 PO 交⊙O 于点 D，则 PD＝3－r. 由圆的割线定理知，PA· PB＝PD· PC， ∴1×3＝(3－r)(3＋r)，∴9－r2＝3，∴r＝ 6. 答案： 6
∴AD＝2AE. ∵AO＝AE＋3， 在 Rt△ADO 中，AO2＝AD2＋OD2， ∴(AE＋3)2＝4AE2＋9，解之得，AE＝2.∴AD＝4. 答案：4
【例 3】 如图， 直线 AB 经过⊙O 上的点 C， 并且 OA＝OB， CA＝CB ，直线 OB 交⊙O 于点 E，D，连接 EC，CD. (1)试判断直线 AB 与⊙O 的位置关系，并加 以证明； 1 (2)若 tan∠E＝2，⊙O 的半径为 3，求 OA 的长．
解析：(1)证明：如图，连接 OC. 因为 OA＝OB，CA＝CB， 所以 OC⊥AB.所以 AB 是⊙O 的切线． 1 CD 1 (2)因为 tan∠E＝2，所以 EC ＝2. 因为△BCD∽△BEC， BD CD 1 所以BC ＝ EC ＝2.设 BD＝x，则 BC＝2x. 又 BC2＝BD· BE，所以(2x)2＝x(x＋6)． 解得 x1＝0，x2＝2. 因为 BD＝x＞0，所以 BD＝2. 所以 OA＝OB＝BD＋OD＝2＋3＝5.
半径、弦心距和半弦长联系起来，是计算长度重要关系式．
变式探究 1．如图，CD是圆O的切线，切点为C，点A，B在圆O上，BC ＝1，∠BCD＝30°，则圆O的面积为________．
答案：π
圆的切线、割线定理的应用
【例 2】 如图， ⊙O 的直径 AB 的延长线与 弦 CD 的延长线相交于点 P，E 为⊙O 上一点， AE ＝ AC ， DE 交 AB 于点 F， 且 AB＝2BP＝4， 则 PF 的长度是____________.
所以∠AOB＝2∠AOE＝120° ， 在优弧 AB 上任取一点 D(不与 A、B 重合)， 1 所以∠ADB＝2∠AOB＝60° ， 所以∠ACB＝180° －∠ADB＝120° .
点评： (1) 与圆中的角有关的定理主要有：圆周角定理、弦
切角定理、圆内接四边形内对角互补等，这些定理都是寻找 圆中角与角之间等量关系的重要依据． (2) 垂径定理将圆的
(1)证明：连接 OP，OM，因为 AP 与⊙O 相切于点 P，所以 OP⊥AP，因为 M 是⊙O 的弦 BC 的中点， 所以 OM⊥BC， 于是∠OPA＋∠OMA＝180° .由圆心 O 在 ∠PAC 的内部，可知四边形 APOM 的对 角互补，所以 A，P，O，M 四点共圆． (2)解析：由(1)得 A，P，O，M 四点共圆，所以 ∠OAM＝ ∠OPM， 由(1)得 OP⊥AP， 由圆心 O 在∠PAC 的内部， 可知∠OPM ＋∠APM＝90° ，所以∠OPM＋∠APM＝90° .
解析：连接 OC，OD，OE，由同 弧对应的圆周角与圆心角之间的关 系，结合题中条件 AE ＝ AC ， 可得∠CDE＝∠AOC，又∠CDE ＝∠P＋∠PFD， ∠AOC＝∠P＋∠C，从而∠PFD＝∠C， PF PD 故△PFD∽△PCO，∴PC＝PO， PC· PD 12 由割线定理知 PC· PD＝PA· PB＝12，故 PF＝ PO ＝ 4 ＝3. 答案：3
指哪两条．
变式探究 2 ．如图， EB 是⊙ O 的直径， A 是 BE 延长线上一点，过点 A 作
⊙O的切线AC，切点为D，过点B作⊙O的切线BC，交AC于点
C，若EB＝BC＝6，则AD＝________.
解析：连接 OD，∵AC，BC 都是⊙O 的切线， ∴CB⊥AB，AC⊥OD，
∴CD＝CB＝6，AD2＝AE· AB，且△ADO∽△ABC. AO AD OD 1 ∴AC ＝ AB ＝ BC ＝2. ∴AB＝2AD. ∵AD2＝AE· AB，
四点共圆问题 【例 4】 如图，已知 AP 是⊙ O 的切线，
P 为切点， AC 是⊙ O 的割线，与⊙ O 交
于B， C两点，圆心 O 在∠ PAC 的内部， 点M是BC的中点．
(1)证明：A，P，O，M四点共圆；
(2)求∠OAM＋∠APM的大小．
思路点拨：要证A，P，O，M四点共圆，可考虑四边形APOM 的对角互补；根据四点共圆，同弧所对的圆周角相等，进行 等量代换，进而求出∠OAM＋∠APM的大小．
点评： (1) 相交弦定理、切割线定理、割线定理、切线长定 理统称为圆幂定理：圆的两条弦或其延长线若相交，各弦被 交点分成的两条线段的积相等． (2) 当割线的两交点在圆内 时为相交弦定理，当割线的两交点在圆外时为割线定理，两 交点重合时为切线，一条上两点重合时为切割线定理，两条
都重合时为切线长定理，应用此定理一定要分清两条线段是
第十章
第二节
直线与圆的位置关系
与圆有关的量的计算
【例 1】 如图，已知⊙O 的半径为 2，弦 AB 的长为 2 3，点 C 是劣弧 ACB 上任一点，(点 C 不与 A、B 重合)，则∠ACB＝__________.
ห้องสมุดไป่ตู้
解析：连接 OA、OB，过 O 作 OE⊥AB，E 为垂足，
则 AE＝BE. 1 在 Rt△AOE 中，OA＝2，AE＝2AB＝ 3， 由勾股定理得 OE＝ OA2－AE2＝1， 所以∠OAE＝30° ，∠AOE＝60° ，