九年级数学切线的判定

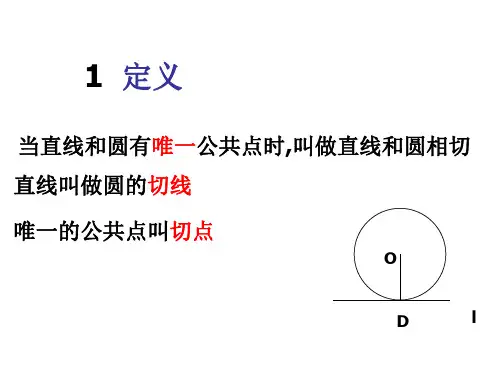
九年级数学圆的切线的知识点数学中的圆是一个常见的几何图形，它有许多有趣的性质，其中之一就是切线。

切线是一个与圆相切于一点且与圆没有其它的交点的直线。

在这篇文章中，我们将探讨九年级数学课程中关于圆的切线的知识点。

1. 切线定义及性质切线是一个特殊的直线，它与圆只有一个交点，且与圆在该点的切线相切。

切线的性质有以下几点：(1) 切线与半径垂直：切线与从切点到圆心的半径垂直相交。

(2) 弦切角相等：切线和过切点的弦所夹的角相等。

(3) 切线长度相等：从圆外的任意一点引切线，得到的切线长度都相等。

2. 切线的判定方法在几何中，判断一条直线是否为圆的切线，有以下两种判定方法：(1) 切线判定法一：若直线与圆只有一个交点，并且该交点到圆心的距离等于圆的半径，则该直线是圆的切线。

(2) 切线判定法二：若直线与圆相交，且与圆的切点处平分被切角，那么该直线也是圆的切线。

3. 切线的性质在解题中的应用切线的性质经常在解题过程中被使用，下面介绍几个常见的应用情况：(1) 切线的长度：我们可以利用切线的性质来求解切线的长度。

根据切线与半径垂直的性质，我们可以使用勾股定理或者勾股定理的变形来求解切线的长度。

(2) 弦的长度：通过切线和弦的切角相等的性质，我们可以利用已知的切线长度和弦的长度来计算未知的切线或者弦的长度。

(3) 切线的方程：切线与圆的关系可以通过方程来表示。

我们可以利用切线判定法一中的条件，得到切线方程的一般形式。

4. 实际生活中的切线应用切线在实际生活中有许多应用，下面介绍几个例子：(1) 轮胎的设计：车辆的轮胎通常是圆形的，轮胎的切线对于保证行驶的稳定性非常重要。

(2) 光学反射：光线在两种介质之间传播时，若入射角等于反射角，则光线与界面的交点所在的直线即为切线。

(3) 经济决策：在经济学中，曲线图表上的切线可以表示某一点的边际效应，帮助决策者做出合理的判断。

总结起来，九年级数学课程中关于圆的切线的知识点包括切线的定义及性质，切线的判定方法，切线性质的应用，以及实际生活中的切线应用。

人教版数学九年级上册判定圆切线的二、五法则判定圆的切线是初中数学的一个重要内容。

同学们在学习时一定要扎实掌握切线的判定。

下面就和同学们谈谈判定圆切线的二、五法则，请同学们学习时加以借鉴。

一方法篇判定切线的两种方法1、定义法：过圆心作直线的垂线，设圆的半径为r，垂线段的长为d，当d=r时，直线就是圆的切线。

特点：垂足需要说明是在已知的圆上的，方法是证明垂线段等于已知的一条半径。

2、判定定理法：经过半径的外端并且垂直于半径的直线是圆的切线。

特点：半径与直线都有了，关键是证明它们的位置关系是垂直。

二、步骤篇在具体判定切线时，同学们要注意如下五条基本原则：1、关注一个等腰三角形---------两腰是半径的等腰三角形。

这个三角形在圆中是经常出现的，一定要引起同学们的高度关注，它主要是提供等角。

2、构造一个圆周角-----遇直径，构造直径上的圆周角，它主要是提供一个直角。

3、连接一条半径-----直线经过的圆上点与圆心的连线。

它主要是提供要垂直的半径。

4、作出一条垂线段------过圆心向所要证是切线的直线作垂线。

它主要是提供一条“准半径”。

5、活用一条原理-------等量代换。

只要同学们能熟记上面的二法五步的基本要求，判定切线就会顺利闯关的。

三应用篇1、等腰三角形+半径，利用三角形的全等证直角判定切线例1如图1，AB是⊙O的直径，BC⊥AB于点B,OC∥AD,求证：CD为⊙O的切线。

分析：点D已经是圆上的点，所以只需连接OD，设法证明DO⊥CD即可。

证明：连接OD，因为OC∥AD,所以∠DAO=∠COB,∠ODA=∠COD.因为OA=OD，所以∠DAO=∠ODA，所以∠COB=∠COD.在三角形COD和三角形COB中，⎪⎩⎪⎨⎧=∠=∠=CO CO COB COD OB OD ，所以△COD ≌△COB ，∠CBO=∠CDO.因为BC ⊥AB 于点B,所以∠CBO=90°，所以∠CDO=90°，所以DO ⊥CD ，所以CD 是为⊙O 的切线。

切线的概念、切线的判定和性质-人教版九年级数学上册教案一、切线的概念1. 切线的定义在圆上取一点P，连接P与圆心O，若通过点P的直线与圆相交于点P，则这条直线称为该圆在点P处的切线。

2. 切线的性质切线只与圆相交于切点，且垂直于半径。

二、切线的判定1. 判定方法1在圆上任取一点P，连接P与圆心O。

若连接P与圆心O的线段与已知直线L 垂直，则L与圆的交点就是切点，而L即为此点处的切线。

2. 判定方法2在圆上任取一点P，连接P与圆心O。

作过点P并与已知直线L平行的直线，与圆相交于点Q。

再连接点Q与圆心O，则Q与L的交点即为圆在点P处的切点，L即为点P处的切线。

三、切线性质的应用1. 切线定理若一条直线与圆相交于点A、B，则与这条直线垂直的切线分别过点A、B。

2. 判定定理在圆上任取两点P、Q，以这两点为端点连一条线段，若该线段平分圆周角，则它的延长线必过圆的圆心。

3. 弦割定理两条互相垂直的弦互相垂直。

4. 弦长定理两条互相垂直的弦所对圆周的两段弧相等。

5. 弧上点角定理圆周上一点的任意两个角所对的弧长相等。

四、练习题1.已知圆O，半径为3.4cm，P为圆上一点，PA为一条直线，且PA=8.1cm。

求PA的垂线与OP的夹角。

2.已知圆的直径是20cm，D,E,F,G均在圆上。

若DE⊥FG，DE=12cm，FG=9cm，求DG的长。

3.已知圆心角ACB的弧度是20度，线段AB上一点D是圆上的一点，求角ADC的角度。

五、课堂小结1.切线的定义和性质。

2.切线判定方法和定理。

3.切线性质的应用。

4.练习题的解答。

六、作业1.完成课堂练习题。

2.独立思考，将切线定理、判定定理、弦割定理、弦长定理和弧上点角定理的证明写出来。