下载文档原格式
第二章平面汇交力系与平面力偶系一、要求1、掌握平面汇交力系合成（分解）的几何法。
能应用平衡的几何条件求解平面汇交力系的平衡问题。
2、能正确地将力沿坐标轴分解和求力在坐标轴上的投影。
对合力投影定理应有清晰的理解。
3、能熟练地运用平衡方程求解平面汇交力系的平衡问题。
4、对于力对点的矩应有清晰的理解，并能熟练地计算。
5、深入理解力偶和力偶矩的概念。
明确平面力偶的性质和平面力偶的等效条件。
6、掌握平面力偶系的合成方法，能应用平衡条件求解力偶系的平衡问题。
二、重点、难点1、 力在坐标轴上的投影，合力投影定理，平面汇交力系的平衡条件及求解平衡问题的解析法。
2、 力对点之矩的计算，力偶矩的概念，平面力偶性质和力偶等效条件。
三、学习指导平面汇交力系合成的结果是一个合力，合力作用线通过力系的汇交点，合力的大小和方向等于力系的矢量和，即∑==+⋅⋅⋅⋅⋅⋅++=ni i n F F F F R 121或简化为∑=F R上式是平面矢量方程，只可以求解两个未知数。
每一个力都有大小和方向两个要素（因为力的汇交点是已知的），因此，方程中只能有两个要素是未知的。
矢量方程的解法有：几何法和解析法。
只有力沿直角坐标轴分解的平行四边形才是矩形。
力在轴上投影的大小等于分力的大小，投影的正负表示分力沿坐标轴的方向。
平面汇交力系平衡的必要和充分条件是力系的合力为零。
即∑R=F这个平面的矢量方程可解两个未知数，解法有几何法和解析法。
（1）平衡的几何条件：平面汇交力系的力多边形封闭。
（2）平衡的解析条件：平面汇交力系的各分力在两个坐标轴上投影的代数和分别等于零即：∑=0YX；∑=0对于平衡方程，和平面汇交力系合成与分解的解析法一样，一般也选直角坐标系。
但在特殊情况下，有时选两个相交的相互不垂直的坐标轴，可使问题的求解简化。
这是因为平衡时合力恒等于零，合力在任一坐标轴的投影也恒等于零，所以，不一定局限在直角坐标系。
合力投影定理与合力矩定理是结构静力计算经常要用到的两个定理。
第二章 平面汇交力系与平面力偶系平面汇交力系与平面力偶系是两种简单力系，是研究复杂力系的基础，本章将分别研究两种力系的合成与平衡问题。
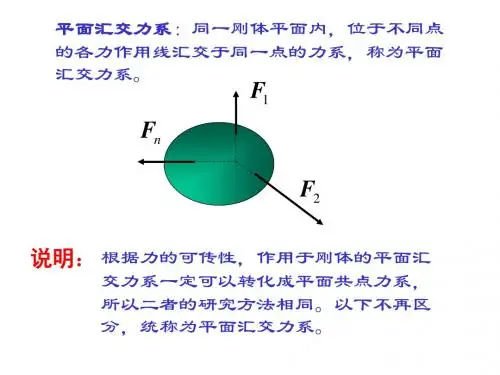
§2-1平面汇交力系合成与平衡的几何法平面汇交力系是指各力的作用线在同一平面内且汇交于一点的力系。
一、平面汇交力系合成的几何法、力多边形法则如图a 所示，作用在刚体上的四个力1F ，2F ，3F 和4F 汇交于点A 。
连续应用平行四边形法则，即可求出通过汇交点A 的合力R 。
合力R 的大小和方向也可用图(b)所示的力三角形法则或力多边形法则得到。
后者，作出图示首尾相接的开口的力多边形abcde ,封闭边矢量ae 即所求的合力。
通过力多边形求合力的方法称为几何法。
改变分力的作图顺序，力多边形改变，如图(c)所示，但其合力不变。
平面汇交力系可合成为通过汇交点的合力，其大小和方向等于各分力的矢量和。
即∑==+++=n i i 1n 21F F F F R 简写为 ∑=F R （2-1）二、平面汇交力系平衡的几何条件平面汇交力系平衡的必要和充分条件是：力系的合力等于零。
其矢量表达式为∑==0F R （2-2）力系平衡的几何条件是：力系的力多边形自行封闭。
例2-1 如图所示，钢梁的重量kN 6N 1063=⨯=P ,︒=30θ，试求平衡时钢丝绳的约束力。
解：取钢梁为研究对象。
作用力有：钢梁重力P ，钢绳约束力AF 和B F 。
三力汇交于D 点 ，受力如图a 所示。
作力多边形，求未知量。
首先选择力比例尺，以1cm 长度代表2kN 。
其次，任选一点e ，作矢量ef ，平行且等于重力P ，再从e 和f 两点分别作两条直线，与图(a)中的A F 、B F 平行，相交于h 点，得到封闭的力三角形efh 。
按各力首尾相接的次序，标出fh 和he 的指向，则矢量和he 分别代表力A F 和B F （如图b 所示）。
按比例尺量得和的长度为：45.3=fh cm ， 45.3=he cm即 45.3145.3=⨯=A F kN ，45.3145.3=⨯=B F kN 从力三角形可以看到，在重力P 不变的情况下，刚绳约束力随角θ增加而加大。
