平面汇交力系与平面力偶系习题课

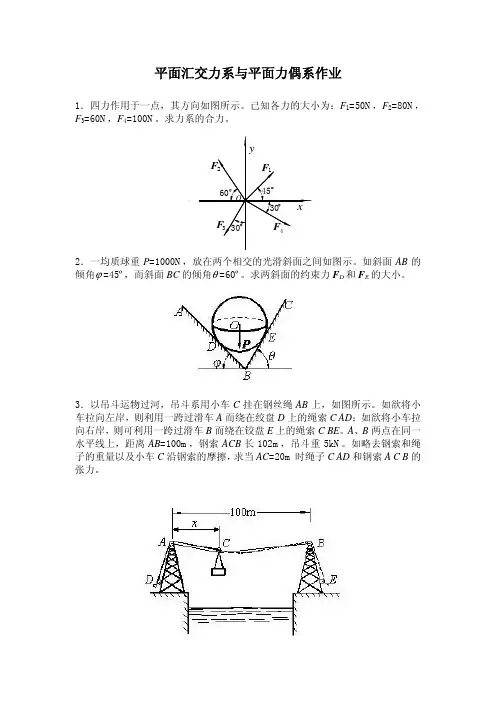
平面汇交力系与平面力偶系作业1．四力作用于一点，其方向如图所示。

已知各力的大小为：F1=50N，F2=80N，F3=60N，F4=100N。

求力系的合力。

2．一均质球重P=1000N，放在两个相交的光滑斜面之间如图示。

如斜面AB的倾角ϕ =45º，而斜面BC的倾角θ =60º。

求两斜面的约束力F D和F E的大小。

3．以吊斗运物过河，吊斗系用小车C挂在钢丝绳AB上，如图所示。

如欲将小车拉向左岸，则利用一跨过滑车A而绕在绞盘D上的绳索C AD；如欲将小车拉向右岸，则可利用一跨过滑车B而绕在铰盘E上的绳索C BE。

A、B两点在同一水平线上，距离AB=100m，钢索ACB长102m，吊斗重5kN。

如略去钢索和绳子的重量以及小车C沿钢索的摩擦，求当AC=20m时绳子C AD和钢索A C B的张力。

4．均质杆AB长l，置于销子C与铅垂面间，如图所示。

不计摩擦力，求平衡时杆与铅垂线间的夹角θ。

5．三个相同的光滑圆柱放置如图示，求圆柱不至于倒塌时θ 角的最小值。

6．杆AB以铰链A及弯杆BC支持，杆AB上作用一力偶，其力偶矩大小为M，顺时针转向，如图所示。

所有杆件的重量不计，求铰链A与C的约束力。

7．图示机构中杆AB 上有一导槽，套在CD 杆的销子E 上，在AB 和CD 杆上各有一力偶作用，如图所示。

己知M 1=1000N ·m ，不计杆重及摩擦。

求机构在图示位置平衡时力偶矩M 2的大小。

8．水平杆AB 由铰链A 与连杆CD 支持于铅垂转轴EF 上，在AB 杆的一端作用有一力偶（F ，F ′）其矩的大小为M 。

设所有杆件的重量不计，求CD 杆的内力及轴承E 与F 处的约束力。

第二章-1 平面汇交力系与平面力偶系一、判别题（正确和是用√，错误和否×，填入括号内。

）2-1 平面汇交力系平衡的充分与必要的几何条件是：力多边形自行封闭。

（√）2-2 力在某一固定面上的投影是一个代数量。

（×）2-3 两个力F1、F2大小相等，则它们在同一轴上的投影也相等。

（×）2-4 一个力不可能分解为一个力偶；一个力偶也不可能合成一个力。

（√）2-5 力偶无合力、不能用一个力来等袒代替，也不能用一个力来平衡；（√）2-6 力偶无合力，也就是说力偶的合力等于零。

（×）2-7 力偶矩和力对点之矩本质上是二样的，讲的是一回事。

（×）2-8 力偶的作用效果取决于力偶矩的大小和转向。

（√）2-9 只要两力偶的力偶矩代数值相等，就是等效力偶。

（√）2-10 力偶中的两个力对同平面内任一点之矩的代数和等于力偶矩。

（√）2-11 力偶只能用力偶来平衡。

（√）2-12 平面力偶系可简化为一个合力偶。

（√）2-13 力偶可任意改变力的大小和力偶臂的长短。

（×）2-14 力偶的两力在其作用面内任意轴上的投影的代数和都等于零。

（√）2-15 若两个力F1、F2在同一轴上的投影相等，则这两个力相等，即F1 = F2。

（×）2-16 若两个力F1、F2大小相等，则在同一轴Ox上投影相等，即F1x = F2x。

（×）2-17 若两个力F1、F2大小、方向、作用点完全相同，则这两个力在任一轴上的投影相等。

（√）2-18 若两个力大小相等、方向相反，则在任一轴Ox上的投影大小相等。

（√）2-19 若两个力平行，则它们在任一轴上的投影相等。

（×）2-20 若两个力在某轴上的投影均为零，则该两力平行。

（√）2-21 图示为分别作用在刚体上A、B、C、D点的4个共面力，它们所构成的力多边形自行封闭且为平行四边形。

由于力多边形自行封闭，所以是平衡的。

第2章平面汇交力系与平面力偶系一、是非题(正确的在括号内打“√”、错误的打“×”)1．力在两同向平行轴上投影一定相等，两平行相等的力在同一轴上的投影一定相等。

( √ )2．用解析法求平面汇交力系的合力时，若选取不同的直角坐标轴，其所得的合力一定相同。

( √ )3．在平面汇交力系的平衡方程中，两个投影轴一定要互相垂直。

( × )4．在保持力偶矩大小、转向不变的条件下，可将如图2.18(a)所示D处平面力偶移到如图2.18(b)所示E处，而不改变整个结构的受力状态。

( × )图2.185．如图2.19所示四连杆机构在力偶的作用下系统能保持平衡。

( × )6．如图2.20所示皮带传动，若仅是包角发生变化，而其他条件均保持不变时，使带轮转动的力矩不会改变。

( √ )图2.19 图2.20 二、填空题1．平面汇交力系的平衡的充要条件是平面汇交力系的合力等于零，利用它们可以求解2个未知的约束反力。

2．三个力汇交于一点，但不共面，这三个力不能相互平衡。

3．如图2.21所示，杆AB自重不计，在五个力作用下处于平衡状态。

则作用于点B的四个力的合力=，方向沿与F的方向相反。

4．如图2.22所示结构中，力对点O的矩为。

5．平面汇交力系中作力多边形的矢量规则为：各分力的矢量沿着环绕力多边形边界的某一方向首尾相接，而合力矢量沿力多边形封闭边的方向，由第一个分力的起点指向最后一个分力的终点。

图2.21 图2.22 6．在直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小相等，但在非直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。

三、选择题1．如图2.23所示的各图为平面汇交力系所作的力多边形，下面说法正确的是( C )。

(A) 图(a)和图(b)是平衡力系 (B) 图(b)和图(c)是平衡力系(C) 图(a)和图(c)是平衡力系 (D) 图(c)和图(d)是平衡力系图2.232. 关于某一个力、分力与投影下面说法正确的是( B )。

第一章静力学公理和物体的受力分析一、选择题1、三力平衡定理是﹍﹍﹍﹍。

①共面不平行的三个力互相平衡必汇交于一点；②共面三力若平衡,必汇交于一点；③三力汇交于一点，则这三个力必互相平衡。

2、三力平衡汇交定理所给的条件是﹍﹍﹍﹍。

①汇交力系平衡的充要条件;②平面汇交力系平衡的充要条件;③不平行的三个力平衡的必要条件；④不平行的三个力平衡的充分条件；3、图示系统只受作用而平衡。

欲使Ａ支座约束力的作用线及ＡＢ成30°角,则斜面的倾角应为﹍﹍﹍﹍。

①0°②30°③45°④60°4、作用在一个刚体上的两个力、，满足=－的条件，则该二力可能是﹍﹍﹍﹍.①作用力和反作用或是一对平衡的力；②一对平衡的力或一个力偶；③一对平衡的力或一个力和一个力偶；④作用力和反作用力或一个力偶。

二、填空题1、已知力沿直线ＡＢ作用，其中一个分力的作用线及ＡＢ成30°角，若欲使另一个分力的大小在所有分力中为最小，则此二分力间的夹角为﹍﹍﹍﹍﹍﹍﹍﹍度。

2、作用在刚体上的两个力等效的条件是﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍﹍。

3、将力沿Ｘ、Ｙ方向分解，已知Ｆ＝100Ｎ，在Ｘ轴上的投影为86。

6Ｎ,而沿Ｘ方向的分力的大小为115。

47Ｎ，则的Ｙ的方向分量及Ｘ轴的夹角为﹍﹍﹍﹍,在Ｙ轴上的投影为﹍﹍﹍﹍。

4、若不计各物体重量，试分别画出各构杆和结构整体的受力图。

第二章平面汇交力系和平面力偶系一、选择题1、已知、、、为作用于刚体上的平面共点力系，其力矢关系如图所示为平行四边形,由此可知﹍﹍﹍﹍﹍﹍﹍。

（1）力系可合成为一个力偶；（2）力系可合成为一个力；（3）力系简化为一个力和一个力偶；（4）力系的合力为零，力系平衡。

2、汇交于Ｏ点的平面汇交力系，其平衡方程式可表示为二力矩形式。

即（）＝0,（)＝0,但必须﹍﹍﹍﹍﹍﹍﹍。

①Ａ、Ｂ两点中有一点及Ｏ点重合；②点Ｏ不在Ａ、Ｂ两点的连线上；③点Ｏ应在Ａ、Ｂ两点的连线上；3、由n个力组成的空间平衡力系，若其中（n－1）个力相交于Ａ点，则另一个力﹍﹍﹍﹍﹍﹍﹍。

第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2—2解：即求此力系的合力，沿OB 建立x 坐标,由解析法，有123cos45cos453RX F X P P P KN==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2—3 解：所有杆件均为二力杆件,受力沿直杆轴线。

(a) 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=(压力)（b ） 由平衡方程有:0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力)（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= （拉力）0.866AC F W=(压力）（d) 由平衡方程有:0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力）0.577AC F W= (拉力）2-4 解：(a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示:由x =∑3cos 45cos 45010RA RB F F P ⋅--=0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2—5解：几何法:系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2—6解：受力如图所示:已知，1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2—7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解:杆AB,AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式,解得：7.32AB F KN=-(受压）27.3AC F KN=（受压）2—9解：各处全为柔索约束，故反力全为拉力,以D,B 点分别列平衡方程（1）取D 点,列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2—10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2—11解:取A 点平衡:x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=(压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-(压力）2-13解：（1)取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q =联立方程后解得: 5RD F Q =2REF Q '=（2）取ABCE 部分,对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

第2章 平面汇交力系与平面力偶系一、目的要求1．平面汇交力系（多个力）合成与平衡的几何法，并能应用平衡的几何条件求解平面汇交力系的平衡问题。

2.能正确地将力沿坐标轴分解和求力在坐标轴上的投影，对合力投影定理有清晰的理解，掌握汇交力系合成的解析法和平衡方程，并能熟练的应用平衡方程求解汇交力系的平衡问题。

3. 理解力对点之矩的概念，并能熟练地计算。

4．深入理解力偶和力偶矩的概念，明确平面力偶的性质和平面力偶的等效条件。

二、基本内容1．平面汇交力系合成的几何法·力多边形法则平面汇交力系可合成为通过汇交点的合力，其大小和方向等于各分力的矢量和。

即∑==+++=n i i 11F F F F F n 2R 或 ∑=F F R合力R F 的大小和方向可用力三角形法则或力多边形法则得到。

作出图示首尾相接的开口的力多边形，封闭边矢量即所求的合力。

2．平面汇交力系平衡的几何条件平面汇交力系平衡的必要和充分条件是：力系的合力等于零。

其矢量表达式为∑==0F F R （2-2） 力系平衡的几何条件是：力系的力多边形自行封闭。

如图2-4所示。

3．力在正交坐标轴系的投影与力的解析表达式力F 在y x ,轴上的投影分别为cos cos sin x y F F F F F αβα=⎫⎪⎬==⎪⎭力的投影是代数量。

4．平面汇交力系合成的解析法合力投影定理：合力在某轴上的投影等于各分力在同一轴上投影的代数和。

平面汇交力系平衡的必要和充分条件是：各力在两个坐标轴上的投影的代数和分别为零。

即00x y F F ⎫=⎪⎬=⎪⎭∑∑ 两个独立的平衡方程，可解两个未知量。

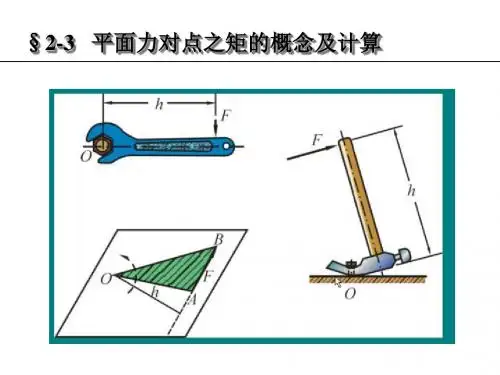
5.平面内的力对点O 之矩是代数量，记为M o (F )ABO Fh M o ∆±=±=2)(F其中F 为力的大小，h 为力臂，∆ABO 为力矢AB 与矩心O 组成三角形的面积。

一般以逆时针转向为正，反之为负。

力矩的解析表达式为： 合力矩定理： 6.力偶和力偶矩：·大小相等，方向相反，作用线平行的两个力称为力偶。