当前位置：文档之家 › 第2章 平面汇交力系与平面力偶系

第2章 平面汇交力系与平面力偶系

  • 格式：doc
  • 大小：1.38 MB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

第二章平面汇交力系及平面力偶系

第二章平面汇交力系及平面力偶系
一、几何法合成（作图法）
1、两力的合成方法——平行四边形法则。
2、多个力的合成。方法——力多边形法 则（依据平行四边形法则）。将汇交
力系各力平行移至首尾相接，起点至
第
终点连线为合力。
一 章
静 力 学 基 础
理论力学教学课件
第一节 平面汇交力系的合成
一、几何法（作图法）
F1
R12
O
F2
F3
R123
同理 ：Ry= F1y+ F2y+ F3y
R FX 2 Fy 2
第二节 平面汇交力系合成的解析法
例 用 解 析 法 求 三 力 的 合 力 。 已 知 F1=100N ，
F2=200N，F3=300N 。
F1
45°
O
F2
解：F1X=F1COS45°=71N F1y=F1sin45°=71N F2X=F2=200N
静 力
自行封闭。
学 基
础
第二节 平面汇交力系的合成与 平衡的解析法
一、解析法合成（计算 ） 1、力在直角坐标轴上的投影
y
a’
A
αF
B
b’
oa
b
x
ab:F在x轴上的投影（Fx). a’b’:F在y轴上的投影（Fy）。
Fx=ab=Fsinα
第
一
Fy=a’ b’= - Fcosα
章
静 力 学 基 础
第二节 平面汇交力系合成的解析法
解：据平衡方程：ΣFx=0 ΣFy=0
ΣFy=-P- FD cos30°-FCBsin30°=0 FCB=-74.6 KN （BC杆受压） ΣF x=-FAB - FD sin30°FCBcos30°=0 FAB =54.6 KN （AB杆受拉）

二章节平面汇交力系与平面力偶系

二章节平面汇交力系与平面力偶系
1、一般地，对于只受三个力作用的物体，且角度特殊 时用 几 何法（解力三角形）比较简便。
2、一般对于受多个力作用的物体，且角度不特殊或 特殊，都用解析法。 3、投影轴常选择与未知力垂直，最好使每个方程中只 有一个未知数。 4、对力的方向判定不准的，一般用解析法。
5、解析法解题时，力的方向可以任意设，如果求出负 值，说明力方向与假设相反。对于二力构件， 一般先 设为拉力，如果求出负值，说明物体受压力。
FAC
FA 450
FAB
FD
图示结构由直角弯杆ABCD与BEG及
直杆CG构成，各杆自重不计，F，a为已
知，求B处的约束力。 FE FA
F
E G
B
力偶实例 2.4 平面力偶
力 偶 实 例 F1
F2
一 力偶的定义：
作用在同一刚体上的大小相等、方向相反、作 用线又不重和的两个平行力所组成的力系称为力偶。 （F ，F′）
6、平面上一个力和一个力偶可以简化成一个 力。
7、如果某平面力系由多个力偶和一个力组成， 该力系一定不是平衡力系。
填空题：
1、同平面的两个力偶，只要 ________相同， 对刚体的外效应相同。
2、力偶________与一个力等效，也_______ 被一个力平衡。
3、平面力偶系合力偶之矩m＝ ________ 。 平面力偶系的平衡条件是________ 。
4、力矩是力使物体绕指定矩心产生________ 效应的度量，其单位是 ________ 。力F对 平面上一点O的力矩等于力的________ 与 力作用线到点的______的乘积，用_____表 示。力矩有正负之分，_____转向规定为正。
填空题：
5、力系合力对平面某点的力矩，等于该力系

t2平面汇交力系与平面力偶系

t2平面汇交力系与平面力偶系
应用场景
在机械工程、土木工程等领域中，需要分析物体在多个力矩作用下的平衡状态，以确定物体的转动状态和稳定性。
03
平面汇交力系与平面力偶 系的联系
力的平移定理
力的平移定理：一个作用在刚体上的力，可以平移而不改变它对刚体的作用，但必 须同时附加一力偶。
力的平移定理描述了力的位置变化对刚体运动的影响，即力的平移不会改变刚体的 运动状态，但需要附加一个与原力等效的力偶。
t2平面汇交力系与平面力偶 系
contents
目录
• 平面汇交力系 • 平面力矩与平面力偶系 • 平面汇交力系与平面力偶系的联系 • 实例分析
01
平面汇交力系
定义与性质
定义
平面汇交力系是指所有力都汇交于一 点或者所有力都位于同一平面内的力 系。
性质
平面汇交力系中，力的方向和大小是 确定的，且所有力的作用线都汇交于 一点或者都位于同一平面内。
02
在进行工程设计和建设时，需 要充分考虑各种力和力矩的作 用，并进行精确的分析和计算 。
03
在机械、航空航天、交通等工 程领域，平面汇交力系与平面 力偶系的应用非常广泛，它们 是工程力学的重要组成部分。
感谢您的观看
THANKS
平面汇交力系主要应用于刚体 在平面运动中的动力学问题，
如机械手、机器人等。
平面力偶系主要应用于分析 旋转刚体的平衡问题，如电
机转子、涡轮机等。
在实际应用中，需要根据问题 的具体需求选择合适的力系进 行分析，以简化问实际工程中的平面汇交力系问题
01
平面汇交力系在工程中常常出现在固定装置的受力分析，例如桥梁、 建筑物的固定连接处。
平面力矩的合成
规则
平面力矩的合成遵循平行四边形定则，即以两个力为邻边作 平行四边形，其对角线矢量等于两个力的力矩之和。

平面汇交力系和平面力偶系

平面汇交力系和平面力偶系

第二章 平面汇交力系与平面力偶系§2.1平面汇交力系合成与平衡的几何法一、汇交力系合成与平衡的几何法 汇交力系：是指各力的作用线汇交于同一点的力系。

若汇交力系中各力的作用线位于同一平面内时，称为平面汇交力系，否则称为空间汇交力系。

1、平面汇交力系的合成先讨论3个汇交力系的合成。

设汇交力系1F ，2F ，3F汇交于O （图1），由静力学公理3：力的平行四边形法则（力的三角形）可作图2，说明)(),,(321F F F F=如图和图所示，其中321F F F F ++=F2F 3F OFO1F 2F 3F12F讨论：1）图2中的中间过程12F 可不必求，去掉12F 的图称为力多边形，由力多边形求合力大小和方向的方法称为合力多边形法则。

2）力多边形法则：各分力矢依一定次序首尾相接，形成一力矢折线链，合力矢是封闭边，合力矢的方向是从第一个力矢的起点指向最后一个力矢的终点。

3）上述求合力矢的方法可推广到几个汇交力系的情况。

结论：汇交力系合成的结果是一个合力，合力作用线通过汇交点，合力的大小和方向即：∑=i F F用力多边形法则求合力的大小和方向的方法称为合成的几何法。

2．平面汇交力系的平衡1F 2F iF 2-n F 1-n F n F设作用在刚体上的汇交力系),,(21n F F F 为平衡力系，即 0),,(21≡n F F F先将121,,-n F F F 由力多边形法合成为一个力1-N F，（∑-=-=111n i i N F F ）0),(),,(121≡≡-n N n F F F F F由静力公理1，作用在刚体上二力平衡的必要充分条件是：1-N F 与n F等值，反向，共线，即n N F F =-1， 可得01=+-n N F F，或0=∑i F结论：平面汇交力系平衡的必要与充分条件是：力系中各力的乖量和为零，用几何法表示的平衡条件是0=∑i F，力多边形自行封闭。

例1． 已知：简支梁AB ，在中点作用力F，方向如图，求反力FA B C45F AF BACα 45FF BF α解：1。

第二章-平面汇交力系与平面力偶系

第二章-平面汇交力系与平面力偶系
负号说明FA方向设反了
FC FA
2FC sin 30 Q 0 FC Q FA Q
例2-3：重物P=20kN，用钢丝绳挂在支架 的滑轮B上，钢丝绳的另一端缠绕在绞车D 上。杆AB 与BC 铰接，并以铰链A、C与 墙连接。如两杆和滑轮的自重不计，并忽 略摩擦和滑轮的大小，试求平衡时杆AB 和BC 所受的力。
平面汇交力系与平面力偶系是两种简单力系， 是研究复杂力系的基础。 本章研究问题： (1)平面汇交力系的几何法与解析法 (2)平面力偶的基本特性 (3)平面力偶系的合成与平衡
§2-1 平面汇交力系合成与平衡的几何法
所有的力在同个平面内且作用线交于一点为平面 汇交力系，三力平衡为其一。
几何法：根据力的平行四边形规则作图得出。
FNA
A
B
FNA
水平坐标系：
FNB
F
y`
30 60 °
x`
FNB F
o`
A B
FNA
FNB
FNA
同样得：
也可以用几何法，画出封闭的力三角形求解，解得此结果。
工件对V形铁的压力与FNA、FNB等值反向。
例：在图示结构中各构件的自重略去不计。在构件AB上作用 一力偶矩为M的力偶，求支座A和C的约束反力。
(a) (b)
FBC、 FAB 均为正值，表示力的假设方向与实际方向 相同，即杆 BC 受压，杆 AB 受拉力。
例：不计杆重。D处受力G，求A、 C处的约束反力。 解：
画受力图
FLASH
Sa大小、方向不知，Sb大小不知，三个未知数
由几何关系：
1 tg tg 3
X 0, Y 0,
SB cos SA cos 0
SB sin SA sin G 0

第二章1平面汇交力系与平面力偶系

第二章1平面汇交力系与平面力偶系

2.欲将碾子拉过障碍物，水平拉力 F 至少多大？ F 3.力 F 沿什么方向拉动碾子最省力，及此时力 多大？
解:取碾子画受力图. 用几何法，按比例画封闭力四边形
R h θ arccos 30 R
F B sin θ F F A F B cosθ P
F 1 1 .4 k N A
由合力投影定理可得：
F F 2 0 0 0 4 3 3 0 0 N 6 3 3 0 N x x
F F 0 2500 3000 N 550 N y y
则合力的大小为：
2 x 2 y 2 2
FF F 6 3 3 0 5 5 0 0 N 8 3 8 6 N
F , X 0 F , Y 0 8 0 4 5 4 R R 0 D A 4 5 PR A
各力的汇交点
(4) 解得
R A 5 P 22 . 4 kN 2
R R D A
1 10 kN 5
力的值为负值,表示假设的指向与实际指向相反.
例4. 简易压榨机如图所示。已知P试求当连杆AB、AC与铅垂线成角时，托板给被压物 体的力。
O
tg
F Ry F Rx
F F
RY
RX
平面汇交力系平衡的必要和充分条 y 件是该力系的合力为零: F R 0
F F 0 Rx X
O
F F 0 Ry X

例2.如图所示吊环受到三条钢丝绳的拉力作用。已知F1=2000N， F2=5000N，F3=3000N。试求合力。
FR F23 F1 F12 F2
F4
FR
F4
F2 F4
FR
F3

理论力学第二章汇交力系与平面力偶系


FBC= 224.23 kN 代入（3）、（4）解得
tan θ = 1.631 , θ = 58.5°
FA= 303.29 kN
y
FBC
FD
C
45°
30°
x
W2
y
FA
θB
x
45°
W1 F'BC
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
投影法的符号法则： 当由平衡方程求得某一未知力的值
y
FBC
B 30°
x
FAB
FD 30° W
b
联立求解,得
FAB= －54.5kN , FBC= 74.5kN
反力FAB为负值，说明该力实际指向与图上假定指向相反。 即杆AB实际上受拉力。
第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡
例2–5 如图已知W1=100 kN， W2=250 kN。不计各
Fx F cos
Fy
Fy F cos
O 2、力在空间直角坐标轴上的投影：
F
Fx x
一次投影法：
Z
Fx F cos Fy F cos
F
O
y
FZ F cos
第二章 汇交力系与平面力偶系
x
★§2–2 空间汇交力系的合成与平衡 二次投影法：
已知力F 和某一平面（oxy)的夹
角为θ，又已知力F 在该平面
杆自重，A，B，C，D各点均为光滑铰链。试求平衡状
态下杆AB内力及与水平的夹角。
A
θB
D
W1
45° C
30°
W2 第二章 汇交力系与平面力偶系
§2–1 平面汇交力系的合成与平衡

第二章：平面汇交力系与平面力偶系

第二章平面汇交力系与平面力偶系一、要求1、掌握平面汇交力系合成（分解）的几何法。

能应用平衡的几何条件求解平面汇交力系的平衡问题。

2、能正确地将力沿坐标轴分解和求力在坐标轴上的投影。

对合力投影定理应有清晰的理解。

3、能熟练地运用平衡方程求解平面汇交力系的平衡问题。

4、对于力对点的矩应有清晰的理解，并能熟练地计算。

5、深入理解力偶和力偶矩的概念。

明确平面力偶的性质和平面力偶的等效条件。

6、掌握平面力偶系的合成方法，能应用平衡条件求解力偶系的平衡问题。

二、重点、难点1、 力在坐标轴上的投影，合力投影定理，平面汇交力系的平衡条件及求解平衡问题的解析法。

2、 力对点之矩的计算，力偶矩的概念，平面力偶性质和力偶等效条件。

三、学习指导平面汇交力系合成的结果是一个合力，合力作用线通过力系的汇交点，合力的大小和方向等于力系的矢量和，即∑==+⋅⋅⋅⋅⋅⋅++=ni i n F F F F R 121或简化为∑=F R上式是平面矢量方程，只可以求解两个未知数。

每一个力都有大小和方向两个要素（因为力的汇交点是已知的），因此，方程中只能有两个要素是未知的。

矢量方程的解法有：几何法和解析法。

只有力沿直角坐标轴分解的平行四边形才是矩形。

力在轴上投影的大小等于分力的大小，投影的正负表示分力沿坐标轴的方向。

平面汇交力系平衡的必要和充分条件是力系的合力为零。

即∑R=F这个平面的矢量方程可解两个未知数，解法有几何法和解析法。

（1）平衡的几何条件：平面汇交力系的力多边形封闭。

（2）平衡的解析条件：平面汇交力系的各分力在两个坐标轴上投影的代数和分别等于零即：∑=0YX；∑=0对于平衡方程，和平面汇交力系合成与分解的解析法一样，一般也选直角坐标系。

但在特殊情况下，有时选两个相交的相互不垂直的坐标轴，可使问题的求解简化。

这是因为平衡时合力恒等于零，合力在任一坐标轴的投影也恒等于零，所以，不一定局限在直角坐标系。

合力投影定理与合力矩定理是结构静力计算经常要用到的两个定理。

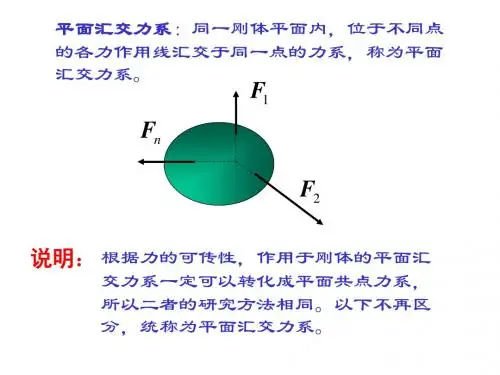
第2章平面汇交力系与平面力偶系

FBA
FBC
FAB
A
' F' FBA BC
B B
B
P
C
F2 F1
C
FCB
解：
y
FBA F2
600
300
（1） 取滑轮为研究对象，将其视为 一个几何点。受力如图所示。
其中 F1= F2 =P = 20 kN （2）选取图示坐标系。列方程
B
FBC
F1
x
X 0, Y 0,
FBA F1cos600 F2cos300 0 FBC F1cos300 F2cos600 0
解：（1）取碾子为研究对 象。 画受力图。
F
F
O B
O B
FB
P
P
A FA
A
（2）根据力系平衡的几何条件，作封闭的力多边形。
按比例，先画已知力，各力矢首位相接。
FB
a.从图中按比例量得
FA=11.4 kN , FB=10 kN 5 kN
FA
0

P
b.也可由几何关系计算
Rh cos 0.866 R
即：若作用在刚体上 {F1 , F2 ,, Fn } {FR }
则：
M O ( FR ) MO (Fi )
i 1
n
在古代，人们没有大型的 起重工具，只能依靠人力和畜力 。在建造宏伟的建筑物时，为了 将巨大的石柱竖立起来，可能采 用了右图所示的方法。其中起关 键作用的是用木材作成的 A 字形 支架。试从力学角度说明采用此 项措施的必要性。
P
解： 取梁为研究对象。 画受力图。
注意：这里所设力 FA 的方向与 实际方向相反。
解：取横梁为研究对象。画受力图。 建立图示直角坐标系。 由平面汇交力系的平衡条件列方程

理论力学第二章平面汇交力系与平面力偶系

FR FRx 2 FRy 2
合力作用点：为该力系的汇交点
2-2 平面汇交力系合成与平衡的解析法
(2)平面汇交力系平衡的充要条件： 各力在两个坐标轴上投影的代数和分别等于零。 ——平面汇交力系的平衡方程
X0,
Y
i 1
n
i
0
只可求解两个未知量
[ 例1 ] 系统如图，不计杆、轮自重，忽略滑轮大小， 已知： P=20kN； 求：系统平衡时，杆AB、BC受力。
解：AB、BC杆为二力杆，
取滑轮B（或点B），画受力图。 用解析法，建图示坐标系
Fix 0
FBA F1 cos 60 F2 cos 30 0

Fiy 0
FBC F1 cos 30 F2 cos 60 0
F1 F2 P
解得： FBC
27.32kN
②应用合力矩定理
mO ( F ) Fx l F y l ctg

m o (Q ) Q l
[例P28 2-4，习题P38 2-10]

[例2]水平梁AB受按三角型分布的载荷作用，如图所示。 载荷的最大值为q，梁长l ,试求合力作用线的位置。
解：在距A端x 的微段dx上， 作用力的大小为q’dx,其中 q’ 为该处的载荷强度。由图可知 ，q’=xq/l。，因此分布载荷合 力的大小为： l
2-2 平面汇交力系合成与平衡的解析法
二、平面汇交力系合成的解析法：
各分力在x轴和在y轴投影的代数 和 等于合力在对应轴上的投影。
FR x X 1 X 2 X 4
X
FR y Y1 Y2 Y3 Y4

Y

i
i
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

·12· 理论力系·12·第2章 平面汇交力系与平面力偶系一、是非题(正确的在括号内打“√”、错误的打“×”)1．力在两同向平行轴上投影一定相等，两平行相等的力在同一轴上的投影一定相等。

( √ )2．用解析法求平面汇交力系的合力时，若选取不同的直角坐标轴，其所得的合力一定相同。

( √ )3．在平面汇交力系的平衡方程中，两个投影轴一定要互相垂直。

( × ) 4．在保持力偶矩大小、转向不变的条件下，可将如图2.18(a)所示D 处平面力偶M 移到如图2.18(b)所示E 处，而不改变整个结构的受力状态。

( × )(a)M图2.185．如图2.19所示四连杆机构在力偶12M M =的作用下系统能保持平衡。

( × ) 6．如图2.20所示皮带传动，若仅是包角α发生变化，而其他条件均保持不变时，使带轮转动的力矩不会改变。

( √)2图2.19 图2.20二、填空题1．平面汇交力系的平衡的充要条件是平面汇交力系的合力等于零，利用它们可以求解 2个未知的约束反力。

2．三个力汇交于一点，但不共面，这三个力 不能 相互平衡。

3．如图2.21所示，杆AB 自重不计，在五个力作用下处于平衡状态。

则作用于点B 的四个力的合力R F =F ，方向沿 与F 的方向相反 。

4．如图2.22所示结构中，力P 对点O 的矩为θsin 21PL 。

5．平面汇交力系中作力多边形的矢量规则为：各分力的矢量沿着环绕力多边形边界的某一方向首尾相接，而合力矢量沿力多边形封闭边的方向，由第一个分力的起点指向最后一个分力的终点。

·13·AB1F4F3F2FF图2.21 图2.226．在直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小相等，但在非直角坐标系中，力对坐标轴的投影与力沿坐标轴分解的分力的大小不相等。

三、选择题1．如图2.23所示的各图为平面汇交力系所作的力多边形，下面说法正确的是( C )。

(A) 图(a)和图(b)是平衡力系 (B) 图(b)和图(c)是平衡力系 (C) 图(a)和图(c)是平衡力系 (D) 图(c)和图(d)是平衡力系2F 1F3F(a) 2F 1F 3F(b) 1F2F 3F4F (c)1F2F3F4F (d)图2.232. 关于某一个力、分力与投影下面说法正确的是( B )。

(A) 力在某坐标轴上的投影与力在该轴上的分力都是矢量，且大小相等，方向一致 (B) 力在某坐标轴上的投影为代数量，而力在该轴上的分力是矢量，两者完全不同 (C) 力在某坐标轴上的投影为矢量，而力在该轴上的分力是代数量，两者完全不同 (D) 对一般坐标系，力在某坐标轴上投影的量值与力在该轴上的分力大小相等3．如图2.24所示，四个力作用在一物体的四点A 、B 、C 、D 上，设1P 与2P ，3P 与4P 大小相等、方向相反，且作用线互相平行，该四个力所作的力多边形闭合，那么( C )。

(A) 力多边形闭合，物体一定平衡(B) 虽然力多边形闭合，但作用在物体上的力系并非平面汇交力系，无法判定物体是否平衡(C) 作用在该物体上的四个力构成平面力偶系，物体平衡由0=∑iM来判定(D) 上述说法均无依据4．力偶对物体的作用效应，取决于( D )。

(A)力偶矩的大小(B) 力偶的转向 (C) 力偶的作用平面 (D) 力偶矩的大小，力偶的转向和力偶的作用平面5．一个不平衡的平面汇交力系，若满足0x F =∑的条件，则其合力的方位应是( A )。

(A) 与x 轴垂直 (B) 与x 轴平行(C) 与y 轴正向的夹角为锐角(D) 与y 轴正向的夹角为钝角图2.24·14· 理论力学 ·14·四、计算题2-1在物体的某平面上点A 受四个力作用，力的大小、方向如图2.25所示。

试用几何法求其合力。

解：在平面汇交力系所在的平面内，任取一点a ，按一定的比例尺，将力的大小用适当长度的线段表示，根据力多边形法则，先作矢量ab 平行且等于方向斜向下的kN 1的力，再从点b 作矢量bc平行且等于方向斜向上的kN 1的力，从点c 作矢量cd 平行且等于kN 2的力，最后从点d 作矢量de平行且等于kN75.0的力，合成得矢量ae，即得到该平面汇交力系的合力F R 大小和方向，如图所示。

从图直接量出：kN F R 284.3=，o R i F 3.206),(=，o R j F 3.116),(=2-2 螺栓环眼受到三根绳子拉力的作用，其中1T 、2T 大小和方向如图2.26所示，今欲使该力系合力方向铅垂向下，大小等于15kN ，试用几何法确定拉力3T 的大小和方向。

解：在平面汇交力系所在的平面内，任取一点a ，按一定的比例尺，将力的大小用适当长度的线段表示，根据力多边形法则，先作矢量ab 平行且等于1T ，再从点b 作矢量bc 平行且等于2T ，从点a 作矢量d a铅垂向下，大小为kN 15的力。

连接c 、d 两点，得矢量cd ，即为拉力3T 的大小和方向，如图所示。

从图直接量出：kN T 2.163=，o30=β。

2-3如图2.27所示套环C 可在垂直杆AB 上滑移，设124kN F .=，216kN F .=，348kN F .=，试用几何法求当α角多大时，才能使作用在套环上的合力沿水平方向，并求此时的合力。

a e dc b 0.75kN图2.256kN图2.26R Fa c3 1F R·15·解：在平面汇交力系所在的平面内，任取一点a ，按一定的比例尺，将力的大小用适当长度的线段表示，根据力多边形法则，先作矢量ab 平行且等于1F ，再从点b 作矢量bc 平行且等于2F ，从点a 作矢量d a水平向右，以c 点为圆心，以3F 的大小为半径画圆，该圆与过a 点的水平线的交点为d 点，连接c 、d 两点，得矢量cd，即为拉力3F 的大小和方向，如图所示。

从图直接量出：o 2.48=α。

连接a 、d 两点，得矢量ad，即为合为的大小和方向，从图量得：kN F R96.4=。

2-4已知1100N F =，250N F =，360N F =，480N F =，各力方向如图2.28所示。

试分别求各力在x 轴和y 轴上的投影。

解：各力在x 轴和y 轴上的投影分别为：N F F x 6.8630cos o 11==，N F F y 5030sin o 11==N F F x 305322=⨯=，N F F y 405422-=⨯-=N F x 03=，N F F y 6033==N F F x 6.56135cos o 44-==，N F F y 6.56135sin o 44==2-5已知图 2.29所示中120k NF =，21414kN F .=，32732kN F .=，试求此三个力的合力。

解：合力在x 轴和y 轴上的投影分别为N F F F F xi Rx 045cos 60cos o2o 1=+-==∑ N F F F FF yiRy045sin 60sin 3o 2o 1=-+==∑N F F F Ry Rx R 022=+=2-6求如图2.30所示各梁支座的约束反力。

(a)(b)(c)(a)By(b)By F(c)NB解：分别选各梁为研究对象，受力分析如图所示。

分别列平衡方程，有(a)∑=0x F 045cos o =-F F Ax∑=0yF 045sin o =-+F F FBy Ay图2.28kN 141F图2.29图2.30·16· 理论力学·16·∑=0)(F A M0245sin 4o =⨯-⨯F F By联立求解，可得：k N 07.745cos o==F F Ax ，kN 54.3245sin o==F F By ， kN 54.345sin o =-=By Ay F F F(b)∑=0xF 0=AxF∑=0y F 0=-+F F F ByAy∑=0)(F A M 024=⨯-⨯F F By联立求解，可得：k N 0=Ax F ，kN 52==FF By ，k N 5=-=By Ay F F F (c)∑=0xF 060cos 45sin o o =--F FF NBAx∑=0yF 060sin 45cos o o =-+F FF NBAy∑=0)(F A M 0260sin 445cos o o =⨯-⨯F FNB联立求解，可得：kN F Ax 33.9=，kN F NB 12.6=，kN F Ay 33.4=2-7压路机的碾子半径R = 40cm ，在其中心O 处受重力W = 20kN ，如图2.31所示。

试求碾子越过厚度为8cm 的石板时，所需的最小水平拉力min F 以及碾子对石板的作用力。

解：选压路机的碾子为研究对象，受力分析如图所示，列平衡方程，有∑=0xF053min 1=-⨯F F N∑=0yF05421=-+⨯W F F N N 碾子越过石板时，有02=N F ，联立求解上式，有kN F 15min =，kN F N 251=2-8水平杆AB 分别用铰链A 和绳索BD 连接，在杆中点悬挂重物G = 1kN ，如图2.32所示。

设杆自重不图2.31·17·计，求铰链A 处的反力和绳索BD 的拉力。

解：选水平杆AB 为研究对象，受力分析如图所示，列平衡方程，有∑=0xF 030cos 30cos oo=-BAF F∑=0y F 030sin 30sin oo=-+G F F BA联立求解上式，有kN F F B A 1==2-9如图2.33所示，杆AB 长2m ，B 端挂一重物G = 3kN ，A 端靠在光滑的铅直墙上，C 点搁在光滑的台阶上。

设杆自重不计，求杆在图示位置平衡时，A 、C 处的反力及AC 的长度。

解：选杆AB 为研究对象，受力分析如图所示，列平衡方程，有∑=0xF 030sin o =-C A F F ∑=0yF030cos o =-G F C联立求解上式，有：k N 464.3=C F ，k N 732.130sin o ==C A F FAC 的长度为：m 5.130sin 12o=⨯-=AC2-10如图2.34所示的起重机支架的AB 、AC 杆用铰链支承在立柱上，并在A 点用铰链互相连接，绳索一端绕过滑轮A 起吊重物G = 20kN ，另一端连接在卷扬机D 上，AD 与水平成30°角。

设滑轮和各杆自重及滑轮的大小均不计。

求平衡时杆AB 和AC 所受的力。

解：选滑轮A 为研究对象，受力分析如图所示，列平衡方程，有∑=0x F 030cos 30cos 30sin o o o =--AB AD ACF F F∑=0yF 030sin 30sin 30cos o o o=-+-G F F FAB AD AC其中kN G F AD 20==，联立求解，有图2.32·18· 理论力学·18·0=AB F ，k N36.34=AC F2-11如图2.35所示，自重为G 的圆柱搁置在倾斜的板AB 与墙面之间，圆柱与板的接触点D 是AB 的中心，各接触处都是光滑的。