当前位置：文档之家 › 板壳理论 课件 chapter1 弹性薄板弯曲的基本理论汇总

板壳理论 课件 chapter1 弹性薄板弯曲的基本理论汇总

  • 格式：ppt
  • 大小：1.66 MB
  • 文档页数：104

下载文档原格式

  / 104

合集下载

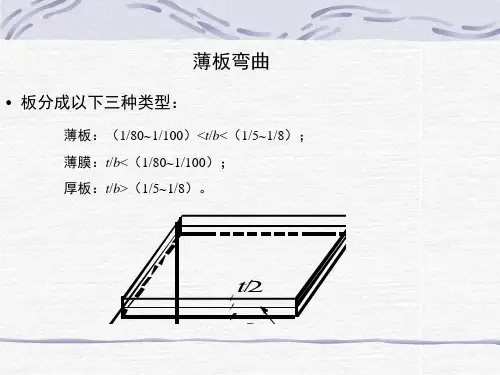
弹性力学板弯曲

弹性力学板弯曲

（x，y，xy）～qb2/t2
（xz，xz y）～qb/t
z～q

由内力表示的平衡微分方程
Qx Q y q0 x y M x M yx Qx 0 x y M xy x M y y Qy 0
2 M xy 2 M y 2M x 2 q0 2 2 x xy y
Qy D

应力与内力的关系
x 12 z Mx 3 t y 12 z My 3 t xy 12 z M xy 3 t
yz
6 t ( z 2 )Q y 3 t 4
2
6 t2 zx 3 ( z 2 )Qx t 4
1 z z z 2q ( ) 2 (1 ) 2 t t
（3）中面各点没有平行于中面的位移。

假定的推论
假定（2）（与梁弯曲问题的互不挤压假定相似）
z=0
z w 0 z
w=w(x,y)
假定（1）（与梁弯曲问题的平面假定相似） zx=zy=0，
w u y ＋ ＝0 y z
w ux z f1 x, y x
w u x ＋ ＝0 x z
RB＝(Myx)B＋(Mxy)B＝2(Myx)B
3w 3w Vx D 3 ( 2 v ) xy 2 x 3w 3w V y D 3 (2 v) 2 x y y
2w RB 2 D(1 v)( ) xy
d 4w 2 q ( x) 1 EI dx 4
与梁的平衡微分方程相比，多了一项（12）。 其原因是：板单位宽度的窄条是处于平面应变状态（y=0）



薄板横截面上的内力
M x z x dz M xy

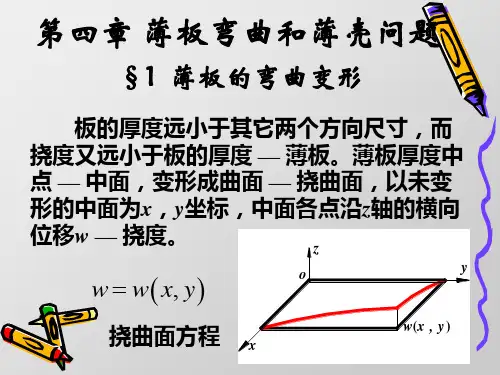
薄板弯曲和薄壳问题

薄板弯曲和薄壳问题

y
Ni 0
0
Ni
刚度矩阵b 刚度矩阵S
kbe se Bb T DBb dxdy kSe se BS T BS dxdy
Kb kbe KS kSe
总体刚度矩阵 K Kb KS
等效节点力
q x, y
Qe
se
N T
0
dxdy
0
Q Qe
K Q
§4 薄壳变形的假设
1
(i k,l, m, n)
M DBe
T
U e 1 2
1
se
D
1
dxdy
1 2
e
T
se BT DBdxdy e
1 e T ke e 2
ke se BT DBdxdy
K ke
总变形能
U
U e
1 T
2
K
不计边界外力，只有面内横向载荷时的外力功为
1
(i=k, l, m, n)
三、单元刚阵
w N(x, y)e
1
x
2
x
2
1
1
y
2 y2
w
2
x
2
1 2
y
2
N e [B] e
1
xy
2 2 xy
应变矩阵
2 2 xy
B Bk Bl Bm Bn
6xi x a4
Dp
1
z
h
M x
2
h
x
zdz
2
h
M xy
2
h
xy
zdz
x
2
h
M y
2
h
y

弹性力学 薄板弯曲

弹性力学 薄板弯曲

10
zx x yx
z
x y
zy y xy
z
y x
将应力分量用挠度 表示的物理方程代入上式，并化
简得：
zx
z
1
Ez
2
2
x
zy
z
1
Ez
2
2
y
由于挠度 不随z 变化，且薄板在上下面的边界条
件为：
zx z t 0, 2
zy z t 0 2
11
将上列二式对z 进行积分，得：
16
将上节给出的应力分量与挠度 之间关系代入，并积分
得：
Mx
D
2
x 2
ห้องสมุดไป่ตู้
2
y 2
My
D
2
y 2
2
x 2
M xy
M yx
D1 2
xy
Qx
D
2
x
Qy
D
y
2
上式称为薄板弯曲问题中内力与变形之间的弹性方程。
17
利用应力分量与挠度 之间的关系、薄板挠曲微分方 程以及内力与形变之间的弹性方程，消去 ，可以给出各
（1）几何方程
在薄板的中面上取一微
小矩形ABCD如图所示。它的 边长为dx和dy，载荷作用后， 弯成曲面A’B’C’D’。设A点的挠
度为 ，弹性曲面沿x和y方
向的倾角分别为 和 ，则
x y
A
dy A
w
D y
z
y
D
dx
w x
Bx
B
C
C
6
B点的挠度为 dx
x
D点的挠度为 dy
y
由
xz
0和

弹性薄板的小挠度弯曲课件

弹性薄板的小挠度弯曲课件
践指导。
06
参考文献
参考文献
总结词：详细描述了弹性力学的基本 原理，包括应力和应变的关系，以及 弹性薄板在受到外力作用时的弯曲变 形规律。
详细描述：在弹性力学中，薄板的小 挠度弯曲是指薄板在受到外力作用时 发生的弯曲变形，其弯曲变形程度较 小，可以忽略不计薄板的剪切变形和 转动惯性。这种变形情况下，薄板的 弯曲变形可以通过挠度（即变形量） 来描述。在弹性力学中，应力和应变 之间的关系由胡克定律（Hooke's Law）描述，即应力与应变成正比， 比例系数为材料的弹性模量。
详细描述
圆形薄板在受到垂直于其平面的力时，会在力的方向上发生弯曲，形成弧形。与矩形薄板类似，这种弯曲程度较 小，也称为小挠度弯曲。在圆形薄板中，各个方向的弯曲程度基本相同，因此圆心位置的应力最大。
实例三：不规则形状薄板的弯曲
总结词
不规则形状薄板在受到垂直于其平面的力时，会发生小挠度弯曲。
详细描述
不规则形状薄板在受到垂直于其平面的力时，会在力的方向上发生弯曲，形成弧形。与矩形和圆形薄 板类似，这种弯曲程度较小，也称为小挠度弯曲。不规则形状薄板的弯曲情况较为复杂，需要考虑各 个方向的弯曲程度以及应力分布。
05
结论与展望
研究结论
结论一
弹性薄板在受到小挠度弯 曲时，其弯曲行为与材料 属性、几何尺寸等因素密 切相关。
结论二
通过理论分析和数值模拟， 我们得到了弹性薄板在小 挠度弯曲下的变形规律和 应力分布。
结论三
实验结果与理论预测和数 值模拟结果基本一致，验 证了理论的正确性和数值 方法的可靠性。小的单元，对每 个单元进行弯曲分析，通过求解每个 单元的平衡方程得到整体的挠度分布。
对于某些特定形状和载荷条件的薄板， 可以通过解析方法直接求解弯曲微分 方程，得到挠度分布的精确解。

板壳理论

板壳理论

球壳
A1=A2= R R1=R2= R
z
椭球壳: (x/a)2 +(y/a)2+ (z/b)2=1
r a 2b2 /(a 2 sin2 b2 cos2 )3 / 2
r a 2 /(a 2 sin2 b2 cos2 )1/ 2
z
s
R
o
y
z


o

y x z

x y
r2
r1
(4) 小挠度假设：略去几何非线性
3
1.2 板壳的内力与应力(应力沿板厚线性分布)
内力素：内力，内力矩
面内 拉力 Tx
N/m z
h/ 2
h / 2

h/ 2
x dz
, Ty
h/ 2
h / 2

面内 y dz 剪力 Txy
N/m
h/ 2
h/ 2
h / 2

xy dz
Ty i Mxy
Ny n Txy My
Nx Tx
j
Mxy
弯矩
Nm/m
Mx
h / 2
h/ 2

x zdz , M y
h / 2

y zdz
Mx T xy
Mx
y
扭矩
Nm/m
M xy
h / 2

xy zdz
My
x Tx
h
Mxy
Ty
Ty 6 M y Txy 6 M xy Tx 6 M x x 2 , y 2 , xy 2 h h h h h h
拱优于梁
5
几种承力结构形式的比较：

《板壳力学》课件

《板壳力学》课件

2 板壳的特点
3 板壳的分类
板壳具有高强度、轻量化、 刚度高、形状复杂、适应 性广等特点，能够承受各 种力学加载。
根据形状、边界条件和受 力特点，板壳可以分为不 同类型，例如矩形板壳、 环形板壳和扭转板壳。
板壳的力学模型和假设
力学模型
板壳的力学模型可以采用理想 化的弹性平面假设，简化了计 算过程，但仍能准确描述板壳 的弯曲和扭转行为。
假设条件
在板壳的力学分析中，我们通 常假设板壳是薄的、具有轴对 称性、材料均匀等条件。
应力假设
为了简化计算，我们通常假设 板壳处于平面应力状态，通过 选择适当的应力假设来近似描 述实际应力分布。
板壳的受力分析方用解析方法进行板壳的受力分析，得到精确的应力和位 移解。
在工程领域，板壳结构广泛应用于汽车车身、 桥梁、储罐、压力容器等领域，具有重要的实 际价值。
航空航天领域
在航空航天领域，板壳结构被应用于飞机机身、 卫星反射镜和火箭燃烧室等部件的设计和制造。
科学研究
对板壳力学的研究不仅在应用层面有重要价值， 还为理论研究和学科发展提供了深厚的基础。
总结和展望
通过本节课的学习，我们深入理解了板壳力学的基本概念、力学模型、受力 分析和稳定性分析等内容。
挠度测量
通过测量板壳的挠度，可以了解 其承载能力和变形情况，在实际 工程中具有重要的应用价值。
失稳分析
失稳分析用于研究板壳的失稳模 态和失稳行为，为结构设计和优 化提供了重要依据。
板壳的应用领域和实际案例
建筑领域
板壳结构广泛用于建筑物的屋盖、墙面、地板 等部位，提供了美观、高效的结构解决方案。
工程领域
2
数值方法
为了解决复杂的板壳结构问题，可以利用数值方法，如有限元分析，对板壳进行数值模拟和 求解。

板壳理论--薄板小挠度弯曲问题及经典解法 ppt课件

板壳理论--薄板小挠度弯曲问题及经典解法 ppt课件

§13.2弹性曲面的微分方程
3.力平衡方程
z
w 表示，取体力分量 Z 0
z xz yz
z x y
zx
2
E
1 2
z2
t2 4
x
2w
zy
2
E
1 2
z2
t2 4
y
2w
z
z
E (z2t2)4w
2(12) 4
推导过程
21
PPT课件
z xz yz z x y
zx
y xy zy 0 y x z
z
xz
yz
Z
0
z x y
x ux,y yv,z wz,xyxvuy,
yzvzw y,zx
uw z x
物理方程
x E1[(x (y z)];y E1[(y (x z)];
z E1[(z (x y)]
xy
8G1xy;yz
G1yz;zx
Ez2
1 2
x
2w
F1
x,
y
zy
2
Ez2
1 2
y
2
w
F2
x,
y
zy z t 0 2
zx z t 0 2
F1x,y81Et22
2w x
F2x,y81Et22
2w y
zx
2
E
1 2
z2
t2 4
x
2w
zy
2
E
1 2
z2
t2 4
y
2w
20
PPT课件
z E (z2t2)4w
z 2(12) 4
22
PPT课件
§13.2弹性曲面的微分方程

《板壳力学》课件

《板壳力学》课件

板壳力学的重要性
总结词
板壳力学在工程实践中具有重要意义，广泛应用于航空航天、船舶、建筑、机械 等领域。
详细描述
板壳力学在工程实践中具有重要意义，是解决复杂结构问题的重要工具。它广泛 应用于航空航天、船舶、建筑、机械等领域，为各种工程结构的优化设计、安全 评估和故障诊断提供了理论基础。
板壳力学的历史与发展
06
板壳力学的未来发展与挑战
新材料与新结构的板壳力学
新材料
随着科技的发展，新型材料如碳纤维 复合材料、钛合金等在航空、航天、 汽车等领域的应用越来越广泛，对板 壳力学提出了新的挑战和要求。
新结构
新型结构如曲面壳体、变厚度板等不 断涌现，需要深入研究其力学性能和 设计方法，以满足工程实际需求。
多场耦合的板壳力学问题
采用一系列简化假设来分析其力学行为。
薄壳弯曲方程
02
描述薄壳在弯曲时的挠度和转角等参数的方程。
薄壳边界条件和载荷
03
分析薄壳在边界条件和各种载荷作用下的弯曲变形和应力分布
。
厚板与厚壳理论
厚板与厚壳定义
厚板和厚壳是指厚度与另外两个尺寸相比不可忽略的板状和壳状 结构。
厚板与厚壳弯曲方程
描述厚板和厚壳在弯曲时的挠度和转角等参数的方程，通常较为复 杂，需要考虑更多的因素。
《板壳力学》ppt课件
目录
• 板壳力学概述 • 板壳力学的基本理论 • 板壳力学的应用 • 板壳力学的数值分析方法 • 板壳力学的实验研究 • 板壳力学的未来发展与挑战
01
板壳力学概述
定义与特点
总结词
板壳力学是研究板和壳体在各种外力作用下的应力、应变和位移分布规律的科 学。
详细描述
板壳力学主要研究板和壳体在受到各种外力作用时的应力、应变和位移分布规 律，包括静力学和动力学问题。它涉及到弹性力学、塑性力学、断裂力学等领 域，是固体力学的一个重要分支。

板壳理论 课件 chapter1 弹性薄板弯曲的基本理论

板壳理论 课件 chapter1 弹性薄板弯曲的基本理论
材料选择与制备：研究新型材料在板壳结构中的应用，提高其强度、刚度和耐久性。
结构分析方法：研究更精确、高效的数值模拟方法，对板壳结构进行应力分析、振动分析和稳定性分析。
实验研究：通过实验手段，对板壳结构进行加载测试、疲劳测试和耐久性测试，验证理论分析的准确性。
汇报人：
安全可靠：实验设计应确保实验过程的安全性和可靠性，避免意外事故的发生
重复性：实验设计应具有重复性，以便验证实验结果的可靠性和可重复性
实验数据的处理与分析
实验数据的收集与整理
实验数据的分析技巧
实验结果的可视化展示
实验数据的处理方法
实验结果与理论预测的比较
实验结果：通过实验测量板壳理论的各项参数，如弹性模量、泊松比等，并记录实验数据。
核工程领域
电子工程领域
建筑与桥梁领域
机械工程领域
航空航天领域
船舶与海洋工程领域
弹性薄板的基本假设
弹性薄板在弯曲时，其材料性质不变
弹性薄板在弯曲时，其边界条件不变
弹性薄板在弯曲时，其厚度不变
弹性薄板在弯曲时，其长度和宽度不变
弹性薄板的弯曲方程
弹性薄板的基本假设
弹性薄板的弯曲方程推导
弹性薄板弯曲方程的意义和应用
是工程结构分析中的重要理论之一
适用于分析细长比大于10的薄板结构
主要研究板和壳的变形及内力分布规律
பைடு நூலகம்
板壳理论是弹性力学的一个分支
板壳理论的发展历程
早期发展：板壳理论的起源和基本概念
中期发展：板壳理论的完善和应用
近期发展：板壳理论的现代研究和应用
未来展望：板壳理论的未来发展趋势和挑战
板壳理论的应用领域
理论预测：根据板壳理论建立数学模型，对实验结果进行预测，并与实验结果进行比较。

板壳理论ppt课件

板壳理论ppt课件
– 弯矩和扭矩： N – 剪力： N/m
26
§1.3 薄板的内力和应力
各应力分量与薄板内力及横向载荷的关系：
x

12M x t3
z
y

12M y t3
z
xy
yx

12M xy t3
z
xz

6Qx t3

t2 4

z2


yz

6Qy t3

t2 4

M
xy

M xy x
dx

dx
变换为一个力偶，力为
F点合M成xy为 向Mx下xy 的dx 合力
u z w v z w 由几何方程得应x变分量：y

x

u x

z
2w x2

y

v y

z
2w y2

xy

v x

u y

2z
2w yx
11
§1.2 薄板弯曲的基本方程
由于是小挠度，所以弹性曲面的曲率和扭率用
w表示为：
x


2w x2
y


2w y2
xy

2
2w yx
应变分量用曲率和扭率表示为：
x zx y z y xy zxy x , y , xy 为板的广义应变。
12
§1.2 薄板弯曲的基本方程
由物理方程得应力分量为：

x

E
1 2
x y
17
§1.2 薄板弯曲的基本方程

140909-板壳力学1

140909-板壳力学1

定
。 zx , zy , z
办法根据平衡方程可以确定它们的值。
第24页，共137页。
第二节 弹性曲面的微分方程
应力
设薄板仅受在上板面作用横向的分布载
荷，其集度为 q q。(x另, y设) 体力分量 fx f y，若0 体力分量 不等于f z 零，把
薄板每单位面积内的体积力和面力归入薄板
上面的面力之中，一并用 表q示，且以z轴
（a)薄板的中面代替了梁的轴线； （b)薄板的弹性曲面代替了梁的弹性曲线； （c)薄板的弯曲代替了梁的平面弯曲； （d)直法线假定代替了梁的平截面假定。
第17页，共137页。
第一节 有关概念及计算假定
计算假定
归纳薄板的计算三个假定：
（1）垂直与中面方向的应变可以不计。
（2）应力分量 xz , zy ,，z 引起的应变
知： f1(x, y) 0, f2 (x, y) 0
有： u w z, v w z
x
y
再由几何方程， x , y可, x用y 挠度 表示w为：
x
u x
2w x 2
z
y
v y
2w y 2
z
x
y
u y
v x
2
2w xy
z
第21页，共137页。
（1-5）
第二节 弹性曲面的微分方程
位移和形变
即有 。 z 0
由弹性力学空间问题几何方程（8～9）中，有：
w 0, w wx, y
z
（1-1）
表明：中面的任一根法线上，薄板全厚度内的 所有各点都具有相同的位移w，即挠度。
第12页，共137页。
第一节 有关概念及计算假定
计算假定
（2）应力分量 xz , zy , ，z 远小于其余三个

薄板弯曲问题

薄板弯曲问题
M y zdzdx
M xy zdzdy
' xy - h/2
- h/2 h/2
- h/2 h/2
扭矩
M
' yx
yx zdzdx
- h/2
h/2
内力与应力的关系
Mx 3 Eh M My 2 12 1 M xy 1 0
2
x y z xy
弯扭变形列阵
几何方程
2w 2 2 4 6 7 x 2 8 y 611xy x 2 w 2 2 6 2 9 x 610 y 612 xy x 2 w 2 x 2 y 3 x 2 3 y 2 5 8 9 11 12 xy
N x1 i 1 0
b2 c2 d 2 0 N x1 1 N x1 0 (2) y b i 2 a2 e2 N x1 最后利用本点1，确 0 (3) , (4) x i 4,1 定a2=b/8，代回
(1)
弹性薄板矩形（R12）单元
弹性薄板矩形（R12）单元
薄板的形函数可以用 广义坐标法，也可以用试 凑法得到。由于单元自由 度为12，因此可有12个广 义坐标，位移模式可设为 如下不完全四次多项式
Q1 1 Mx1 4
My1
w3 2 y z 3
x
x3 y3
w a1 a2 x a3 y a4 x 2 a5 xy a6 y 2 a7 x 3 2 2 3 3 3 a8 x y a9 xy a10 y a11 x y a12 xy
物理方程
应变
位移函数
薄板在弯曲变形后，薄板的法线没有伸缩；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

0,
3w y 3
(2
)
3w x 2y
0
( y b)
(1.3.9)
在两条自由边的交点上，例如图1.4的B点处，有总 的集中反力
RB RBA RBC
M yx
B
M xy
B 2 Mxy
B
根据(1.2.4)式，上式又可写为
RB
2D1
2w xy
B
(1.3.10) (1.3.11)
第一章 弹性薄板弯曲的基本理论
因此，如果B点没有支承对板施加此集中力，板
微分方程的解还需要满足角点条件,即在x=a, y=b
处 2w 0 xy
(1.3.12)
如果在B点处有支座可以对薄板施加反力，则有
下述角点条件,即在x=a, y=b处
w0
(1.3.13)
此时反力大小由(1.3.11)式给出。
第一章 弹性薄板弯曲的基本理论
▪ 边界条件
y2 b2
2
1
(1.4.2)
显然，上式满足在边界上w = 0的边界条件。
在边界上有 考虑到
w x
4mx a2x2 a2y2 b210
w y
4my b2
x2 a2
y2 b2
1
0
w w x w y n x n y n
(1.4.3) (1.4.4)
可见挠曲函数同样满足了在边界上 w 0的条件。
如 图 1.4 所 示 ， 在 x=0 的边缘为简支边；y=0边 为 固 支 边 ； x=a 和 y=b 两 边为自由边。
图1.4 板的边界条件
第一章 弹性薄板弯曲的基本理论
▪ 简支边界
➢ 边界处没有外加弯矩
w Mx 0 ( x 0)
M x
h2
x zdz
h 2
D
2w x 2
2w
y 2
M yx
M yx x
dx
M yx
M yx x
dx
单位长度的横剪力 M yx
x
第一章 弹性薄板弯曲的基本理论
因此，可以认为在边界上任意一点处作用有一折算
剪力
Vy
Qy
M yx x
(1.3.6)
同时可以看到，此时在边界的两端有未被抵消的集
中剪力R
RAB
M yx
,
A
RBA M yx B
(1.3.7)
▪ 考虑任一边界（不一定是自由边界）上所受的扭矩Myx。 ▪ 在微段CD上：
内力Myxdx
▪ 在微段DE上：
内力
M
yx
M yx x
dx
dx
在C处有一集中力Myx
在D处有一反向集中力Myx
在D处有一集中力
M
yx
M yx x
在E处有一反向集中力M yx
dx
M yx x
dx
在D处作用由扭矩折算的横剪力
n
第一章 弹性薄板弯曲的基本理论
（4）确定挠度函数 将式(1.4.2)代入薄板的微分方程中，得
D
24m a4
16m a2b2
24m b4
q
(1.4.5)
由上式解得m后不难得到
w
q
x2 a2
y2 b2
2 1
8D
3 a4
2 a2b2
3 b4
(1.4.6)
上式即为本问题的精确解，这是因为式(1.4.6)满足
第一章 弹性薄板弯曲的基本理论
▪ 薄板弯曲理论的求解方法（位移解法）
几何方程
物理方程
平衡微分方程 （运动方程）
弹性薄板的 基本微分方程 （运动方程）
边界条件 （初始条件）
问题的解--板内各点位移
第一章 弹性薄板弯曲的基本理论
§1.3 边界条件
板的计算问题归结为寻求一个函数，这个函 数必须满足基本微分方程，此外在板的周边还应 该满足某些静力条件或运动条件，这就是所谓的 边界条件。
了基本微分方程和全部的边界条件。
第一章 弹性薄板弯曲的基本理论
（5）求解内力及应力分量
将(1.4.6)式代入(1.2.4)和(1.2.10)式，就可以得到 板的内力分量Mx，My，Mxy，Qx和Qy。
将内力分量代入(1.2.14)式，即可求得薄板的全 部应力分量及应变分量。[练习]
『注意』全部非零的应力分量为9个（x，y， z，xy＝yx，xz＝zx，yz＝zy），应变分量为3 个（ ex，ey，gxy)。
于是自由边上的边界条件可以表示为在y=b处：
M y 0,
Vy
Qy
M yx x
0
( y b)
(1.3.8)
后一边界条件表示总的分布剪力等于零，它将原有
的两个边界条件合而为一。
第一章 弹性薄板弯曲的基本理论
注意到(1.2.4)和(1.2.10)式，(1.3.8)可以改写为
2w y 2
2w x 2
第一章 弹性薄板弯曲的基本理论
解：（1）薄板的微分方程
D 2 2 w
4w
D
x
4
2
4w x 2y 2
4w
y4
q
（2）边界条件 w w 0
n
（3）取满足边界条件挠度函数
其边界方程可以表示为
x2 a2
y2 b2
1
(1.4.1)
第一章 弹性薄板弯曲的基本理论
试取挠度函数的表达式为
w
m
x2 a2
边界条件 （初始条件）
问题的解--板内各点位移
第一章 弹性薄板弯曲的基本理论
§1.4 简单例题
薄板问题的求解就是寻求满足基本微分方程和相 应边界条件的挠曲函数。本节通过几个简单的例子 来展示薄板问题的求解过程。
例1 均布载荷作用 下周边固支的椭圆 板。如图1.6所示.
a
x
b
y
图1.6 周边固支的椭圆板
▪ 固支边界
w w 0 ( y 0) y
(1.3.4)
▪ 自由边界
➢ 边界上没有外载荷作用
M y M yx Qy 0 ( y b)
(1.3.5)
第一章 弹性薄板弯曲的基本理论
在薄板弯曲的近似理论中，可以将(1.3.5)中的 后两个条件合并为一个。
图1.5 边界上的扭矩
第一章 弹性薄板弯曲的基本理论
如果设 a ，则椭圆板就成为跨度为2b的平面 应变情形下的固支梁；如果设a=b，就可以得到 周边固支圆板的准确解答[习题] 。
第一章 弹性薄板弯曲的基本理论
▪ 求解步骤
（1）薄板的微分方程 （2）边界条件 （3）取满足边界条件挠度函数
M y
h 2 2w w yxzd2z
h 2
0
D(
xy2w2 0)
2w
x 2
➢
边界M 处xy 有M外yx 加h 弯2 xy矩zdzM D(1
w
0,
Mh x
2
M
(
x
0)
)
2w xy
w 0,
2w x 2
M D
( x 0)
(1.3.1) (1.3.2) (1.3.3)
第一章 弹性薄板弯曲的基本理论
➢ 固支边界 w w 0 y
( y 0)
➢ 简支边界
2w w x2 0 ( x 0)
➢ 自由边界
2w y 2
2w x 2
0,
3w y 3
(2
)
3w x 2y
0
( y b)
第一章 弹性薄板弯曲的基本理论
▪ 薄板弯曲理论的求解方法（位移解法）
几何方程
物理方程
平衡微分方程 （运动方程）
弹性薄板的 基本微分方程 （运动方程）