二年级专题第四讲：数几何图形的个数

春季班第一讲——我会数图形
【知识点】：
一、规则图形（肩并肩手拉手排成一排）
线段
角
1. 分类数（恰含法）。

每层个数×层数＝总数
【例】数一数图中有多少个三角形？
每层个数：3＋2＋1＝6（个） 层数：2层
总数：6×2＝12（个） 一共12个。

2. 多层长方形
每层个数×层数＝总数
（长边线段总数）×（宽边线段总数）＝总数
【例】数一数下图中一共有多少个长方形？
总数：6×3＝18（个）一共18个。

础、提高、尖子）
2. 数一数图中有多少个正方形？（提高、尖子）
3. 数一数下图中一共有多少个三角形？（基础、提高）
4. 数一数，图中共有个长方形，个三角形，条线段。

（尖子）
【学习建议】：
本讲讲的是数图形的方法，根据不同类型的图形有不同的巧妙方法，同学们要仔细辨认图形种类，像是规则图形和多层图形都是有巧妙方法的；如果是不规则图形，那么一定要注意分类，数的时候思路要清楚，这样才不会数错。

第4讲：图形计数（二）姓名：
知识要点
同学们知道图中有多少个三角形吗？我们可以这样想：图中的小三角形一共有4个，大三角形有1个，所以共有5个三角形。

在计数时，做到有次序、有条理，不遗漏，也不重复，而且迅速。

这就需要掌握规律和方法，才能数得又对又快。

这一讲，我们将介绍一些简单的数图形的规律和方法。

例1：数一数，图中共有多少个三角形？
练习1、：数一数，图中有多少个三角形？
例2：数一数，图中共有多少个三角形？
练习2：数一数，图中有多少个三角形？
例3：数一数，图中有多少个长方形。

练习3：数一数，下图中一共有多少个长方形。

例4：数一数，图中共有多少个小方块。

练习4：数一数，图中共有多少个小方块。

例5：数一数图中有多少个长方形，有多少个三角形。

练习5：图中有多少个长方形和三角形？
总结归纳：
本讲主要介绍了数三角形、长方形和小方块的方法。

三角形、长方形的数量可以借助数线段的方法来计算，而数小方块要学会分层、分类，就会一个不多一个不少地数出。

奥赛题
自我检测得分：
1、数一数，图中有多少个三角形。

2、数一数，图中有多少个长方形。

3、数一数，图中有多少个小方块。

4、下面图形中线段比三角形多几个？
课后练习
1、数一数，图中有多少个三角形？
3、数一数，图中有多少个小方块？
4、数一数，图中有多少个三角形，多少个长方形。

第6讲 图形个数一、知识要点 同学们，你想学会数图形的方法吗？要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

二、精讲精练【例题1】数出下图中有多少条线段？【思路导航】方法一：我们可以采用以线段左端点分类数的方法。

以A 点为左端点的线段有：AB 、AC 、AD 3条；以B 点为左端点的线段有：BC 、BD 2条；以C 点为左端点的线段有：CD 1条。

所以，图中共有线段3+2+1=6（条）。

方法二：把图中线段 AB 、BC 、CD 看做基本线段来数，那么，由1条基本线段构成的线段有：AB 、BC 、CD 3条；由2条基本线段构成的线段有:AC 、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3+2+1=6（条）线段。

练习1：（1）数出下图中有多少条线段？（2）数出下图中有几个长方形？E A B C D D A BC【例题2】数出图中有几个角？【思路导航】数角的个数可以采用与数线段相同的方法来数。

方法一：以OA 为一边的角有：∠AOB 、∠AOC 、∠AOD 3个；以OB 为一边的角还有：∠BOC 、∠BOD 2个；以OC 为一边的角还有：∠COD 1个。

所以，图中共有角3+2+1=6（个）。

方法二：把图中∠AOB 、∠BOC 、∠COD 看做基本角来数，那么，由1个基本角构成的角有：∠AOB 、∠BOC 、∠COD 3个；由2个基本角构成的角有: ∠AOC 、∠BOD 2个；由3个基本角构成的角有：∠AOD 1个。

所以，图中一共有3+2+1=6（个）角。

练习2：数出图中有几个角？【例题3】数出右图中共有多少个三角形？ 【思路导航】方法一：我们可以采用按边分类数的方法。

图形的个数
数出几何图形的个数是数学思考的一种，由于几何图形千变万化，错综复杂，要想数出图形的个数，关键一点是要掌握有条理、有次序地数图形的方法，常用的方法有按顺序数和分类数两种。

一、数线段、角和三角形。

线段总数都等于从1开始的连续自然数的和，最后一个加数正好等于线段的总点数-1。

因此我们只要数出线段的总点数便可求出线段总数，即：线段总数= 1+2+3+4+……+（总点数-1）=总点数×（总点数-1）÷2。

1、数出下面几何图形的个数。

2、数出下面几何图形的个数。

二、数长方形和正方形
1、数长方形：长方形个数=[长边的总点数×（总点数-1）÷2]×宽边的[总点数×（总点数-1）÷2]
2、数正方形：边长是一个长度单位的正方形个数＋边长是两个长度单位的正方形个数＋边长是三个长度单位的正方形个数＋……。

图形计数（二）☜知识要点我们已经认识了很多图形，如直线、射线、线段、正方形、三角形等。

如果一幅图形只是单一的一种，并只有一个的，我们叫他基本图形；如果一幅图形中还包含一些小的图形，就叫组合图形。

在数图形的过程中，你会发现一些规律和方法。

根据组合图形的特点要选用不同的方法来计数，主要有以下几种方法：1．按顺序数，按规律数，做到不遗漏。

2．分类数，先数基本图形，再数由两个至多个基本图形组成的图形，这样不易重复。

☜精选例题【例1】：数一数，图中共有多少个角？思路点拨：我们已经知道，从一点起，用尺子向不同方向画两条线，就得到一个角，角有一个顶点，两条边。

我们可以按顺序数；也可以分类数，先数基本图形，再数由两个至多个基本图形组成的图形。

☝标准答案：方法一：按顺序数。

以OA为固定边的角一共有4个；以OB为固定边的角一共有3个；以OC为固定边的角一共有2个；以OD为固定边的角只有1个。

角的个数共有：4+3+2+1=10（个）方法二：分类数，先数基本图形，再数由两个至多个基本图形组成的图形。

这幅图中基本角的个数有4个；由2个基本角组成的角的个数有3个；由3个基本角组成的角的个数有2个；由4个基本角组成的角的个数只有1个。

角的个数共有：4+3+2+1=10（个）✌活学巧用1．数一数，图中有多少个角？2．数一数，图中有多少个角？【例2】：数一数，图中共有多少个三角形？☝思路点拨：我们已经知道数角的方法，在上图中，不难看出有3个基本三角形，再数由两个至多个基本图形组成的三角形。

☝标准答案：这幅图中基本三角形的个数有3个；由2个基本三角形组成的个数有2个；由3个基本三角形组成的个数只有1个。

三角形的个数共有： 3+2+1=6（个）✌活学巧用1．数一数，图中共有多少个三角形？2．数一数，下图中共有多少个三角形？ 【例3】：数一数，图中有多少个三角形？☝思路点拨：可以分层来数。

☝标准答案：先数最上面一层：有三个基本三角形，能数出3+2+1=6（个）再数上、下两层可以合起来的：同样有3+2+1=6（个）一共有三角形：6+6=12（个）活学巧用1．数一数，图中有多少个三角形？2．数一数，图中有多少个三角形？【例4】：数一数，图中有几个三角形？☝思路点拨：这样的题目，一般多用小块分类的方法数图形。

一升二年级思维数学讲义第一讲数图形学习目标思维目标：运用合理的方法来数出相应图形的数量，培养细心和耐心。

数学知识：比一比知识梳理思维：数图形时不能乱数，要根据一定的规则和方法，才能数出正确的个数。

数学：会对各种类型的题目和计算进行比较。

精讲精练【例1】数一数，图中有几个正方形，几个长方形，几个圆，几个三角形。

点金术：每次数一种图形，按一定的次序数，每数一个可以作个记号，如：“√”，可数得：正方形有5个，长方形有3个，圆有4个，三角形有6个。

试金石：1、圆有（）个；三角形有（）个；正方体有（）个。

2、下图由哪些图形组成？这些图形各有几个？【例2】数一数，图中有几个点●●●●●●●●●●●●●●●点金术：从上往下一行一行地数，这样既不会重复，也不会遗漏，最后把每行的个数加起来。

计算结果是：1+2+3+4+5=15（个）试金石：1、数一数，下图中共有（）个点。

●●●●●●●●●●●●●●●●●●●●●2、数一数，下图中共有（）个点。

●●●●●●●●●●●●●●●●●●●●●●●●●【例3】数一数，下图中共有（）个三角形。

点金石：先数单个三角形有2个，2个合并有1个，2+1=3个试金石：1、数一数，下图中共有（）个长方形。

2、数一数，下图中共有（）个正方形。

3、数一数，下图中共有（）个三角形。

数学园地：比一比 比大小也有学问哦！你会吗？算一算、比一比。

看谁填得又快又对。

1. □中最大填几？ □＋6＜15 □－5＜911－4＞□ 15＞□＋82.填□：7＋□＝12―4 16―□＝11－3 3＋8－□＝4□＋6－9＝7 □＋3＋4＝12 □―6―3＝53.在○填上“＞”、“＜”或“＝”：9＋5○8＋5 9＋6○8＋7 15―9○15―812―9○13―8 16―8○17―9 8＋8○9+24、填（ ）：（1） 4＋7＞12－（ ）（ ）中可填：（2）6＝19－（ ）－8 18＝7＋（ ）＋46＝（ ）―7―3 （ ）―4＝16―7―45、找规律填数（1）1、3、6、10、（ ）、（ ）、28（2）19、2、17、5、15、8、（ ）、（ ）6、 1、3、6、7、8、9这六个数字填入（ ）内，使两个算式成立（ ）+（ ）=（ ） （ ）—（ ）=（ ）学习导航基础训练综合提高1.选择正确的问题（在括号内打“√”，再计算）白兔有16只（1）白兔比黑兔少几只？（）黑兔有7只（2）黑兔比白兔多几只？（）（）（3）白兔和黑兔相差几只？（）2.依次填得数：6＋7 __―8 __＋9 __－7 __＋8 ＝11―4 __＋9 __－8 _＋5 __－6 ＝3、如果□□＝☆☆☆☆＝△△△那么：□□＋☆＝（）个☆□□－△△△＝（）个☆4、在里填数，使每条线上3个数的和等于中间的数（数字不能重复）。

第四讲：数几何图形的个数“数几何图形的个数”是趣味图形问题的一种。

数图形虽然很简单，但重复计数和遗漏是经常出现的错误，在细心的同时还要掌握方法和技巧。

一、数线段1. 数出下列每条线段上线段的总条数。

分析与解：数线段的时候一定按一定的顺序数，否则就会出现重复或遗漏。

数时可以先数最基本的小线段，再数两条基本线段组成的线段，再数三条基本线段组成的线段，……，最后把各种“线段”条数相加起来。

法一：照下面的方法数(以第2小题为例)：3+2+1=6（条）法二：(规律) 线段总条数都是从1开始的几个连续自然数的和，而且最后一个加数正好和最基本线段数相同。

（1）（条）（2）（条）（3）（条）二、数角2. 数出右图中总共有多少个角.分析与解：在∠AOB内有三条角分线OC1、OC2、OC3，∠AOB被这三条角分线分成4个基本角，那么∠AOB内总共有多少个角呢？首先有这4个基本角，其次是包含有2个基本角组成的角有3个（即∠AOC2、∠C1OC3、∠C2OB），然后是包含有3个基本角组成的角有2个（即∠AOC3、∠C1OB），最后是包含有4个基本角组成的角有1个（即∠AOB），所以∠AOB内总共有角：4＋3＋2＋1＝10（个）.令狐老师注：数角的方法可以采用例1数线段的方法来数，就是角的总数等于从1开始的几个连续自然数的和，这个和里面的最大的加数是角分线的条数加1，也就是基本角的个数.【巩固】数一数右图中总共有多少个角？分析与解：因为∠AOB内角分线OC1、OC2…OC9共有9条，即9+1=10个基本角.所以总共有角：10+9+8+…+4+3+2+1=55（个）.三、数三角形3. 如右图中，各个图形内各有多少个三角形？分析与解：方法一：(1)先数图中包含一个小三角形个数：△ABD、△ADE、△AEF、△AFC 共4个三角形.(2)再数由两个小三角形组合在一起的三角形个数：△ABE、△ADF、△AEC 共3个三角形，(3)以三个小三角形组合在一起的三角形：△ABF、△ADC 共2个三角形，(4)最后数以四个小三角形组合在一起的只有△ABC一个.所以图中三角形的个数总共有：4+3+2+1=10（个）.方法二：我们就可以把数三角形问题转化为数线段问题了。

《数图形的学问》讲义在我们的日常生活和学习中，经常会遇到需要数图形个数的问题。

比如，数一数一个几何图形中有多少个三角形、长方形或者圆形等等。

这看似简单的任务，其实蕴含着不少学问。

一、数图形的基本方法1、分类计数法当面对复杂的图形组合时，我们可以先将图形按照一定的标准进行分类。

比如，对于三角形，可以按照大小、形状或者位置等进行分类，然后分别计数，最后将各类的数量相加。

2、顺序计数法按照一定的顺序来数图形，这样可以避免重复或者遗漏。

例如，从上到下、从左到右，或者从大到小等顺序。

3、标记计数法在数图形的过程中，可以对已经数过的图形做一个小标记，这样能够清楚地知道哪些图形已经被数过，防止重复计数。

二、简单图形的计数1、线段的计数假设有 n 个点在同一条直线上，那么线段的总数为 n×（n 1)÷2 。

例如，有 5 个点，线段的数量就是 5×（5 1)÷2 ＝ 10 条。

2、角的计数同样，如果在一个顶点引出 n 条射线，那么角的总数也是 n×（n 1)÷2 。

3、三角形的计数在一个大三角形中，若内部有 n 个点，与三角形的三个顶点相连，那么三角形的总数为 1 ＋ 2 ＋ 3 ＋… ＋ n 。

三、组合图形的计数1、多层图形比如一个由多个长方形组成的大图形，我们可以先数出一层有多少个长方形，然后再看有多少层，最后相乘得到总数。

2、包含嵌套图形对于包含嵌套的图形，先从最外层开始数，逐步向内部推进，注意不要遗漏被嵌套在内部的小图形。

四、实际应用中的数图形1、建筑设计在建筑设计图纸中，需要准确数出各种形状的构件数量，以确保材料的准备和施工的顺利进行。

2、拼图游戏玩拼图时，通过数图形可以帮助我们更好地了解拼图的组成和结构，从而更快地完成拼图。

3、数学考试在数学考试中，经常会有关于数图形个数的题目，这要求我们熟练掌握数图形的方法，快速准确地得出答案。

五、数图形的易错点1、重复计数由于没有按照一定的顺序或者方法，导致同一个图形被多次计数。

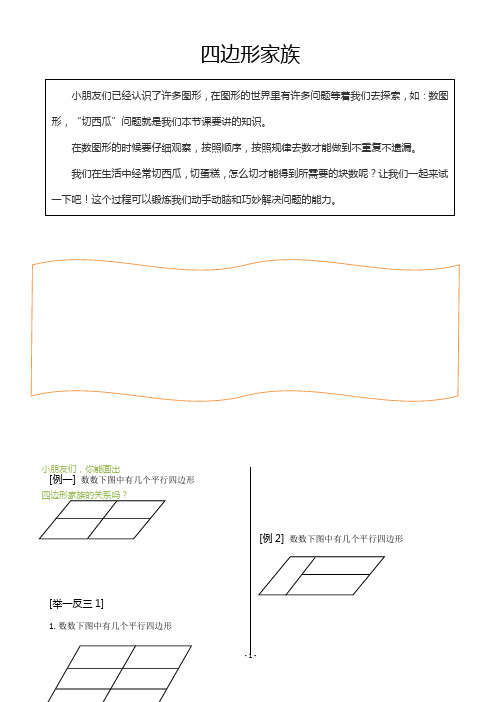
四边形家族[例一] 数数下图中有几个平行四边形
[举一反三1]
1.数数下图中有几个平行四边形[例2] 数数下图中有几个平行四边形
小朋友们已经认识了许多图形，在图形的世界里有许多问题等着我们去探索，如：数图形，“切西瓜”问题就是我们本节课要讲的知识。

在数图形的时候要仔细观察，按照顺序，按照规律去数才能做到不重复不遗漏。

我们在生活中经常切西瓜，切蛋糕，怎么切才能得到所需要的块数呢？让我们一起来试一下吧！这个过程可以锻炼我们动手动脑和巧妙解决问题的能力。

小朋友们，你能画出
四边形家族的关系吗？
[举一反三2]1.数数下图中有几个平行四边形
[例三]
一个月饼竖直切2刀最多能切几块？竖直切3刀最多能切块?竖直切4刀、切5刀呢？竖直切n刀呢？
[举一反三3]
1.一块圆形塑料板，竖直切3刀最多能切成几块？切4刀呢？
2.一个西瓜，竖直切5刀，最多能切多少块？切9刀呢？
3.一个生日蛋糕，竖直切2刀最多能切成几块？切6刀呢？
[例四]
一个菠萝，分给11个小朋友吃，每个小朋友吃1块，如果竖直切，最少要切几刀？[举一反三4]
1.一个西瓜，分给22个小朋友吃，每个小朋友吃1块，竖直切最少要切几刀？
2.幼儿网老师拿来一个大西瓜，分给16个小朋友吃，每个小朋友吃1块，这位老师竖直切，最少要切几刀？
3.一个大南瓜，竖直切成29块，最少要切几刀?
[例五]
一个月饼，切成8块,最少要切几刀？
[举一反三5]
1.小米过生日，同学们为她买了一个大蛋糕，小米要把它分成12块。

小米最少要切几刀，怎么切？
2.妈妈要把一块豆腐切成14块，想一想，妈妈最少要切多少刀？。

几何图形的计数(基本图形)我们已经学习了一些几何图形的有关知识，这些图形有线段、角、三角形、长方形、正方形、梯形、平行四边形，这一讲数学课外兴趣活动就教大家数数图形的个数。

有的同学说，“我们都四年级了，数图形个数谁不会，还用教吗？”请看这里有几条线段,&127;可能你会不加思索地说“2条”，你看到的是这样两条,&127;可是实际上还有一条你数漏了，所以这一题正确的回答应是“3条”。

如果一条直线上有100个点，线段有多少条呢？&127;用数的办法是非常麻烦的，那么今天我们就要用列表找规律的方法研究数基本图形的方法。

例1：数出下图有多少条线段？分析:线段有两个端点，从第一个端点出发的线段有4条，从第二个端点出发的线段有3条，从第三个端点出发的线段有3条，从第四个端点出发的线段有3条，从第五个端点出发的线段有0条。

线段总数共有4+3+2+1+0=10(条)方法二:如果称相邻的两端点组成的线段为基本线段,那么中有4条基本线段,其中的两条基本线段组成的线段有3条,其中由三条基本线段组成的线段有2条其中由四条基本线段组成的线段有1条线段总数是4+3+2+1=10(条)小结:由例1我们可以看出线段总数的计算是有一定规律的,&127; 我们可以用列表的方法找出计算线段总数的公式:图形端点数基本线段数线段总数2 1 13 2 2+1=34 3 3+2+1=65 4 4+3+2+1=10………规律:基本线段数=端点数-1线段总数=基本线段数+(基本线段数-1)+(基本线段数-2)+…+2+1例2:数出下图一共有多少个角?分析:角是由同一点引出两条射线组成的图形,由例1&127;你能设计出一个表格来找出数角总数的规律吗?图形射线数基本角数角总数2 1 13 2 2+1=34 3 3+2+1=6………这一题同样也有两种数法:方法一:由第一条射线出发的角有4个由第二条射线出发的角有3个由第三条射线出发的角有2个由第四条射线出发的角有1个共有4+3+2+1=10(个)方法二:基本角有4个由两个基本角组成的角有3个由三个基本角组成的角有2个由四个基本角组成的角有1个角总数为4+3+2+1=10(个)规律:基本角数=射线数-1角总数=基本角数+(基本角数-1)+(基本角数-2)+…+2+1例3:数数下图共有多少个三角形?分析:有了例1与例2的知识你能自己找出规律吗?方法一:从A点出发的三角形个数是3个从B点出发的三角形个数是2个从C点出发的三角形个数是1个三角形总数是3+2+1=6(个),恰好与底边有多少条线段的得数相同方法二:从顶角看,角的总数也恰好与三角形个数相同:顶角共有3+2+1=&127;6(个)角, 三角形共有6个角你能写出数三角形的公式吗?三角形总个数=基本三角形个数+(基本三角形个数-1)+(基本三角形个数-2)+…+2+1例4:数数下图共有多少个长方形?(包括正方形)分析:长方形的长和宽都是线段,由线段构成的长方形个数一定与线段数有关,横着看: 每一排的长方形个数共有3+2+1=6(个)&127;恰好与长的线段总数相同:竖着看:有3排2+1=3,恰好与宽的线段总数相同,&127;一共有(3+2+1)×(2+1)=18(个)长方形。

二年级图形的个数一、知识要点同学们，你想学会数图形的方法吗？要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

二、精讲精练【例题1】数出下图中有多少条线段？【思路导航】方法一：我们可以采用以线段左端点分类数的方法。

以A 点为左端点的线段有：AB 、AC 、AD 3条；以B 点为左端点的线段有：BC 、BD 2条；以C 点为左端点的线段有：CD 1条。

所以，图中共有线段3+2+1=6（条）。

方法二：把图中线段 AB 、BC 、CD 看做基本线段来数，那么，由1条基本线段构成的线段有：AB 、BC 、CD 3条；由2条基本线段构成的线段有:AC 、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3+2+1=6（条）线段。

练习1：（1）数出下图中有多少条线段？（2）数出下图中有几个长方形？E A B C D D A BC【例题2】数出图中有几个角？【思路导航】数角的个数可以采用与数线段相同的方法来数。

方法一：以OA 为一边的角有：∠AOB 、∠AOC 、∠AOD 3个；以OB 为一边的角还有：∠BOC 、∠BOD 2个；以OC 为一边的角还有：∠COD 1个。

所以，图中共有角3+2+1=6（个）。

方法二：把图中∠AOB 、∠BOC 、∠COD 看做基本角来数，那么，由1个基本角构成的角有：∠AOB 、∠BOC 、∠COD 3个；由2个基本角构成的角有: ∠AOC 、∠BOD 2个；由3个基本角构成的角有：∠AOD 1个。

所以，图中一共有3+2+1=6（个）角。

练习2：数出图中有几个角？【例题3】数出右图中共有多少个三角形？【思路导航】方法一：我们可以采用按边分类数的方法。

二年级奥数：巧数图形体系所属体系板块：第三级上能力培养：分类思考、数形结合思想体系对接：第一级下《有趣的平面图形》第三级下《飞速图形计数》预热知识一、分类法1、打枪法2、恰含法3、分大小【例】下图你能数出多少条线段? 【例】下图共有多少个长方形?【解析】分类法（打枪法）【解析】分类数（恰含法）总：4+3+2+1=10（个）总：3+2+1=6（个）答：共10个. 答：共6个.【例】下图你能数出多少个正方形?【解析】分类数（大小）1个小正方形：4个 4个小正方形：1个总： 4+1=5（个）答：共5个.二、巧数图形（分层数）1、 总数=每层个数相加 每层个数=上层个数+看得见【例】下图中的小方块有几个? 【解析】巧数图形（分层数）总：1+4+5=10（个）答：有10个.课前思考1、 正方形如何计数呢?2、 小方块如何计数呢?3、 如何利用学过的乘法来进行计数?4、一年级秋季要求背的1-10的三角形数还记得吗?1个1+3=4（个） 4+1=5（个）典型例题【分析】方法一：分类数（方向）方法二：分类数（部分）横：1+2+3+4=10（根）三角形数量：1+2+3+4=10（个）左斜：1+2+3+4=10（根）总：10×3=30（根）右斜：1+2+3+4=10（根）答：共30根.总：3×10=30（根）答：共30根.巧数图形知识点精讲知识点一、分类数1、大小2、方向（横、竖、斜）3、部分【例】下图你能数出多少个正方形? 【例】下图共有多少根小棒?【解析】分类数（大小） 【解析】方法一：分类数（方向） 1个小正方形：3×3=9（个） 横：7×2=14（根） 4个小正方形：2×2=4（个） 竖：8根9个小正方形：1个总：14+8=22（根） 总：9+4+1=14（个） 方法二：分类数（部分） 答：共14个. 6×3+4=22（根）答：共22根.二、巧数图形（分层数）2、 总数=每层个数相加每层个数=上层个数+露出脑袋 3、 看不见=总数-看得见【例】下图中看不见的小方块有几个? 【解析】巧数图形（分层数）总：1+4+5=10（个）见：1+3+3=7（个）不见：10-7=3（个） 答：有3个.三、拆补法拆：分部分、加一加 补：看整体、减一减四、特殊的数1个1+3=4（个） 4+1=5（个）1、三角形数第几个三角形数=1+2+3+4+……+几【例】第8个三角形数是几? 【例】15是第几个三角形数?【解析】1+2+3+4+5+6+7+8=36 【解析】1+2+3+4+5=15 答：是36. 答：第5个数.2、正方形数第几个正方形数=几x几【例】第4个正方形数是几? 【例】25是第几个正方形数?【解析】4×4=16 【解析】5×5=25 答：是16. 答：是第5个.巧数图形练习题目1、下图你能数出多少个正方形?2、下图共有多少根小棒?3、下图中看不见的小方块有几个?4、在钉子板上围正方形，共可以围出多少个?答案解析1、知识点：分类数（大小）1个小正方形：13个4个小正方形：6个9个小正方形：1个总：13+6+1=20（个）答：共20个.2、知识点：分类数（方向）横：3×3=9（根）竖：4×2=8（根）总：9+8=17（根）答：共17根.3、知识点：巧数图形（分层数）总：1+3+5+5=14（个）1个1+2=3（个）3+2=5（个）5个见：1+2+3+3=9（个）不见：14-9=5（个）答：有5个.4、知识点：分类数横①：9+4+1=14（个）斜②：4个斜③：2个总：14+4+2=20（个）图①图②图③答：共20个.。

第6讲 图形个数一、知识要点同学们，你想学会数图形的方法吗？要想不重复也不遗漏地数出线段、角、三角形、长方形……那就必须要有次序、有条理地数，从中发现规律，以便得到正确的结果。

要正确数出图形的个数，关键是要从基本图形入手。

首先要弄清图形中包含的基本图形是什么，有多少个，然后再数出由基本图形组成的新的图形，并求出它们的和。

二、精讲精练【例题1】数出下图中有多少条线段？【思路导航】方法一：我们可以采用以线段左端点分类数的方法。

以A 点为左端点的线段有：AB 、AC 、AD 3条；以B 点为左端点的线段有：BC 、BD 2条；以C 点为左端点的线段有：CD 1条。

所以，图中共有线段3+2+1=6（条）。

方法二：把图中线段 AB 、BC 、CD 看做基本线段来数，那么，由1条基本线段构成的线段有：AB 、BC 、CD 3条；由2条基本线段构成的线段有:AC 、BD 2条；由3条基本线段构成的线段有：AD 1条。

所以，图中一共有3+2+1=6（条）线段。

练习1：（1）数出下图中有多少条线段？（2）数出下图中有几个长方形？ 【例题2】数出图中有几个角？【思路导航】数角的个数可以采用与数线段相同的方法来数。

方法一：以OA 为一边的角有：∠AOB 、∠AOC 、∠AOD 3个；以OB 为一边的角还有：∠BOC 、∠BOD 2个；以OC 为一边的角还有：∠COD 1个。

所以，图中共有角3+2+1=6（个）。

方法二：把图中∠AOB 、∠BOC 、∠COD 看做基本角来数，那么，由1个基本角构成的角有：∠AOB 、∠BOC 、∠COD 3个；由2个基本角构成的角有: ∠AOC 、∠BOD 2个；由3个基本角构成的角有：∠AOD 1个。

所以，图中一共有3+2+1=6（个）角。

练习2：数出图中有几个角？【例题3】数出右图中共有多少个三角形？【思路导航】方法一：我们可以采用按边分类数的方法。

以PA 为边的三角形有：△PAB 、△PAC 、△PAD 、3个；以PB 为边的三角形还有：△PBC 、△O DC B APBD 2个；以PC 为边的三角形还有：△PCD 1个。