简单图的一种计数方法
- 格式:pdf
- 大小:353.85 KB
- 文档页数:7

图形的计数(四年级奥数秋季思维训练教程)教学内容:第二讲图形的计数(四年级秋季思维训练教程)课时:第一、二课时课型:新授课教学目的:知识与技能理解并掌握数线段的两种方法:基本线段法、定端点法。
学会灵活地将数图形(三角形、正方形、长方形等)问题转化为数线段问题。
过程与方法通过引导学生复习旧知,鼓励学生总结归纳数线段的基本方法,培养学生的观察能力、抽象概括能力,增强学生探究问题的本领。
在观察、分析图形的过程中,要逐步培养学生掌握从特殊到一般的研究问题的方法。
情感态度与价值观在观察、总结归纳数线段的基本方法的过程中,体会探索新知的乐趣,养成善于思考,勇于探索,乐于交流的习惯。
在数图形个数时,要求按一定的顺序去做,做到不遗漏,不重复,提高学生的逻辑思维能力,养成严密的数学思维习惯。
教学重、难点:重点:通过观察、分析复杂图形并数出其中基本图形的个数的过程中,促进学生掌握类比转化的方法,培养学生分析和解决问题的能力。
难点:如何将复杂图形的计数问题转化为线段的计数问题教具、学具准备:教学过程:复习旧知,凝疑导入同学们,看看我左手上是什么?(粉笔)数数有几只?(三只)。
再看看老师右手上拿了什么?(纸)瞅瞅它们共有几张呢?我们两三岁时家人就开始教我们数数了,所以刚刚那两个问题对同学们来说都是小菜一碟,有没有?但是,不知,同学们还是否记得我们之前学过一种稍微复杂一点的数数问题---数线段。
下面我们来简单地复习一下:问题一:数一数下面图形中共有多少条线段?(10条)线段:有两个端点的直线组成的图形要求:不遗漏不重复展示与总结:定端点法:4+3+2+1=10(条)基本线段法:有4条基本线段由两条基本线段组成的线段:3条由三条基本线段组成的线段:2条由四条基本线段组成的线段:1条共有4+3+2+1=10(条)这道题有没有唤起同学们对以前学过知识的记忆呢?同学们应该都知道,学习是一个连续且不断发展的过程,随着我们年龄和年级的不断增加,我们会对同一个大问题进行更深入的研究,所以,理所当然,数数问题也需要我们对它进行更深一步的探究。

第二讲图形计数几何图形计数问题往往没有显而易见的顺序,而且要数的对象通常是重叠交错的,要准确计数就需要一些智慧了.实际上,图形计数问题,通常采用一种简单原始的计数方法-一枚举法.具体而言,它是指把所要计数的对象一一列举出来,以保证枚举时无一重复、.无一遗漏,然后计算其总和.正确地解答较复杂的图形个数问题,有助于培养同学们思维的有序性和良好的学习习惯.一:简单图形计数的方法。
二:复杂图形计数的方法和找规律的方法。
例(1)数出右图中总共有多少个角分析:在∠AOB内有三条角分线OC1、OC2、OC3,∠AOB被这三条角分线分成4个基本角,那么∠AOB内总共有多少个角呢?首先有这4个基本角,其次是包含有2个基本角组成的角有3个(即∠AOC2、∠C1OC3、∠C2OB),然后是包含有3个基本角组成的角有2个(即∠AOC3、∠C1OB),最后是包含有4个基本角组成的角有1个(即∠AOB),所以∠AOB内总共有角:4+3+2+1=10(个)解:4+3+2+1=10(个)答:图中总共有10个角。
例(2 )数一数共有多少条线段?共有多少个三角形?分析:①要数多少条线段:先看线段AB、AD、AE、AF、AC、上各有2个分点,各分成3条基本线段,再看BC、MN、GH这3条线段上各有3个分点,各分成4条基本线段.所以图中总共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条).②要数有多少个三角形,先看在△AGH中,在GH上有3个分点,分成基本小三角形有4个.所以在△AGH中共有三角形4+3+2+1=10(个).在△AMN与△ABC中,三角形有同样的个数,所以在△ABC中三角形个数总共:(4+3+2+1)×3=10×3=30(个)解::①在△ABC中共有线段是:(3+2+1)×5+(4+3+2+1)×3=30+30=60(条)②在△ABC中共有三角形是:(4+3+2+1)×3=10×3=30(个)答:在△ABC中共有线段60条,共有三角形30个。
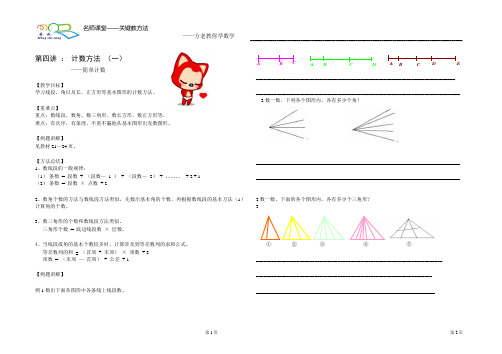
_________________________________________________________________________________________________第四讲 : 计数方法 (一)——简单计数【教学目标】学习线段、角以及长、正方形等基本图形的计数方法。
【重难点】重点:数线段、数角、数三角形、数长方形、数正方形等。
难点:有次序,有条理,不重不漏地从基本图形出发数图形。
【例题讲解】见教材21—24页。
【方法总结】1、数线段的一般规律:(1) 条数 = 段数 + (段数— 1 ) + (段数— 2) + 。
+ 2 + 1 (2) 条数 = 段数 × 点数 ÷ 22、数角个数的方法与数线段方法类似,先数出基本角的个数,再根据数线段的基本方法(1)计算角的个数。
3、数三角形的个数和数线段方法类似。
三角形个数 = 底边线段数 × 层数。
4、当线段或角的基本个数较多时,计算涉及到等差数列的求和公式。
等差数列的和 = (首项 + 末项) × 项数 ÷ 2 项数 = (末项 — 首项) ÷ 公差 + 1【例题讲解】例1.数出下面各图形中各条线上线段数。
______________________________________________________________________________________________________________________________________________________________2.数一数,下列各个图形内,各有多少个角?2.数一数,下面的各个图形内,各有多少个三角形?3.① ② ③ ④ ⑤______________________________________________________________________________________________________________________________________________C B A DA B CD E A B C_________________________________________________________________________________________________3、数出下面各图里长方形的个数。

巧数图形第一级下有趣的平面图形本讲中认识各种平面图形的特点,然后通过简单的图形计数问题,初步培养学生数图形的好习惯.第三级上巧数图形本讲通过一些趣味不规则的图形计数问题,让学生进一步理解乘法的应用问题.第三级下我会数图形本讲学习平面图形的计数方法,培养学生分类计数的好习惯.第三级上巧数图形第一级下有趣的平面图形(一年级秋季第三讲)第三级下我会数图形(二年级秋季第一讲)第3级上·超常班·教师版猜谜语一数真离奇,自己加自己;自己减自己,自己乘自己;自己除自己,得数在一起;相加八十一,猜猜它是几?小朋友们很想知道答案吧!答案就藏在讲义中,仔细找一找.第3级上·超常班·教师版火眼金睛考眼力课前复习下图是由14个小正方形组成的图形.在这个图形中包含有苹果的正方形,共有多少个?猜一猜下图每个图中看不见的小方块有几个?第3级上·超常班·教师版【例题分析】课前通过这两个题的铺垫,让学生很快融入到学习中.第一道题,我们要注意引导学生在数图形的时候不重复、不遗漏,那么在这个图形中包含苹果的正方形一共有6个,包含在1个小正方形里面的有1个,包含在4个小正方形里面的有3个,包含在9个小正方形里面的有2个,一共有6个.第二道题中要求我们数出我们看不见的小正方体,主要培养学生的空间想象能力.在这二个图形中第一个图形看不见的小正方体有3个,第二个图形看不见的小正方体有4个.小朋友们都是数数的小能手,在生活中有很多需要我们通过数数来解决的问题,在解决问题时数数的方法有很多,你会用什么方法来数呢?今天这节课就让我们这些小能手们再次来比试一下吧!小朋友们,请你数一数下面的图形里面有多少个第3级上·超常班·教师版【例题分析】在数的过程中,我们要按顺序来计数.首先我们来看横行,每一横行能数出3个.再来看竖行,每一竖行能数出3个.这样在这个图形中,一共能数出121224+=个第3级上·超常班·教师版【例题分析】⑴摆出一个长方形,一共用了多少根小棒?可以这样数横着的小棒有8216⨯=(根)竖着的小棒一共有9根,合起来一共有16925+=(根)。

有关计数法的简单问题计数问题是数学竞赛经常涉及的问题。
有关计数的方法,我们在此给大家举几个简单例子。
(一)枚举法枚举法就是把所要计数的对象一一列举出来,最后计算总数的方法。
例1有4个球,分别写上号码:1,2,3,4;有4个抽屉,也分别写上号码:一、二、三、四。
现在往每一个抽屉里放一个球,使其中恰有两个抽屉上的号码与球上的号码相同。
求满足以上放球要求的方法共有多少种?解:我们用1,2,3,4表示四个球;用一、二、三、四表示四个抽屉,则满足要求的放法为:可见满足要求的放法共有6种。
例2 某旅游团在a、b、c三个城市游览,规定今天在这个城市,明天一定去另一个城市。
问从a城出发,第5天又回到a城的旅游路线有几种?解:第一天是在a城,从a城出发有两条路线,一条是去b城,一条是去c城。
若第二天在b城,又有两条路线,一条去a城,一条去c城;若第二天在c城,同样也有两条路线,一条去a城,一条去b城,……。
见下图:可见,满足条件的路线有6条。
用枚举法计数时,一定注意遵循“不重、不漏”的原则。
(二)分组法对于数目较大的数学问题,难以用枚举法一一列举,就需要用“分组法”来计数了。
分组法是指把要计数的对象分成几组,每一个对象必须属于一个组,并且只属于一个组,把各个组的计数相加得到总数的方法。
例3用1元,5角,2角,1角四种纸币各一张,一共可以组成几种不同的币值?解:可以按照纸币的张数进行分组:只有一张纸币时,币值有4种;有两张纸币时,币值有6种;有三张纸币时,币值有4种;有四张纸币时,币值有1种。
∴共有4+6+4+1=15种不同的币值。
例4 如图所示,地图上有A,B,C,D,E,F六个地区,现在用红、黄、白、绿、蓝;五种颜色,对每一个地区涂一种颜色,且使相邻地区的颜色不同,问一共有几种不同的涂色方法?解:做此题前,大家首先应该明确计数问题中最常用、最基本的两个原理:加法原理:完成某件事情可以有两类途径,第一类途径中有 m种方法,第二类途径中有n种方法,则完成这件事共有m+n种方法;乘法原理:完成某件事需要分成两步才能完成,第一步中有m种方法,第二步中有n种方法,则完成这件事共有m×n种方法。
计数方法考点图解技法透析1.计数计数,通俗地说就是数数,即把我们研究的对象的个数数出来.在计数时应遵循的原则是:既不重复也不遗漏.2.计数问题中常运用的方法(1)穷举计数法:当研究对象比较简单数目也不大时,穷举法是最基本而又简单的方法,即把对象的所有可能一一列举出来,最后再求出总数.(2)分类计数法:将研究对象按一定标准分类,然后逐步计数,得出总数,这种方法要用到加法原理.(3)分步计数法:当研究对象较复杂时,为了有序而又正确地思维,我们需要将其分成若干步,然后将每一步的方法数相乘,便可得出总数,这种方法要用到乘法原理.(4)递推过渡法:当研究的对象数目较多又比较复杂时,我们常通过对较少数量对象的观察,采用从简单到复杂,从特殊到一般,探究其变化的规律,最后计算出总数.(5)加法原理和乘法原理:当研究的对象比较复杂,且数目较大时,计数时常常要用到如下两原理:①加法原理:完成一件事情,共有n类办法,第一类办法中又有m1种不同的方法,第二类办法中有m2种不同的方法,第三类办法中又有m3种不同的方法……,第n类办法中有mn种不同的方法,那么完成这件事情共有:m1+m2+m3+…+m n种不同方法.②乘法原理:完成一件事情,共分n个步骤,第一步中又有m1种不同方法,第二步中又有m2种不同方法,第三步中又有m3种不同方法…….第n步中有m n种不同方法,那么完成这件事情共有:m1·m2·m3…·m n种不同方法.3.几何计数问题(1)简单图形个数的计算:这类问题中出现的图形的组成一般比较简单,没有过多的限制条件,但图形数量和计算量都很大,此类计数问题通常需要根据具体问题寻求一定的规律和运用一定的计数方法来解决.(2)条件图形个数的计算:这类问题的图形数目较多且较复杂,所求的是满足某种限制条件的几何图形的个数,解决此类问题的关键是对限制条件的分析,这些条件的要求往往决定了所求图形的不同情况和种类,此为分类计数的重要依据.(3)分割或包围图形个数的计算:它们是指用一类几何图形(如直线)去分割另一类几何图形(如平面或其他封闭图形),或者一类封闭图形包含另一类封闭图形,解决此类问题,除了掌握必要的分割与包含的几何知识之外,还需要借助有关统计的方法和技巧.名题精讲考点1 分类枚举法计数例1 在1到300这300个自然数中,不含有数字3的自然数有_______个.【切题技巧】利用分类枚举法,按数的位数分类;即不含有数字3的一位数有几个;不含数字3的两位数有几个;不含数字3的三位数有几个,最后求出总数.【规范解答】∵不含有数字3的一位数有8个;不含有数字3的两位数有72个;不含有数字3的三位数有162个.∴不含有数字3的自然数共有8+72+162=242个.【借题发挥】分类枚举法就是将所研究对象按某一标准分类,然后把研究对象的各种可能一一列举出来,最后数出总数的方法,这种方法要用到加法原理.在运用枚举法时,必须无一重复,无一遗漏,且枚举法常与分类讨论结合运用,故称为分类枚举法.【同类拓展】1.在1000以内的自然数中,各位数字之和等于16的有多少个?考点2 分步法计数例2 某城市街道如图,一个居民要从A处前往B处,如果规定,只能沿从左向右或从上向下的方向走,那么该居民共有几条可选择的路线?【切题技巧】本例看起来复杂,但可以从简单情况入手寻找规律,按从上向下,从左向右的顺序,从简单情况分步来看复杂问题.如先考虑简单情况如图(1)中的正方形,可知以A到C的方法有2种,再考虑如图(2)中的情况,可以从A到D的方法共有3种……【规范解答】从简单情况入手,先考虑如图(1)中的小正方形,不难发现,从A到C 共有2种方法;再考虑如图(2)中的情况,同样可知:从A到D共有3种方法……从而可总结出下述规律:到右下角终点的走法等于它所在小正方形右上角和左下角走法之和,故依次标出每个小正方形的走法不断累加,即可得到答案.由图(3)可知共有40种走法.【借题发挥】(1)分步计数法就是指当所研究对象较复杂时,为了有序而又正确地思维,将问题分成若干步,最后求出各步的总数.(2)在利用分步法计数时,要克服盲目性和随意性,一定要按照法则或顺序进行、从简单情况人手分步来思考复杂问题是解决问题的常用技巧.(3)分步法常与分类法结合求解.【同类拓展】2.在期中考试中,同学甲、乙、丙、丁分别获得第一、第二、第三、第四名,在期末考试中,他们又是班上的前四名,如果他们当中只有一位的排名与期中考试的排名相同,那么排名情况有_______种可能;如果他们排名都与期中考试中的排名不同,那么排名情况有_______种可能.考点3 递推过渡法计数例3 小美步行上楼的习惯是每次都只跨一级或两级,若她要从地面(0级)步行到第9级,问她共有多少种不同的上楼梯的方式.【切题技巧】因为楼梯台阶较多,我们可以先考虑以简单入手.(1)若只有1级台阶,则只有唯一上楼梯方式;(2)若有2级台阶,则有两种上楼梯的方式:①一级一级地上;②一步两级地上;(3)若有3级台阶,则有三种上楼梯的方式:①一级一级地上,②先一级后2级地上,③先2级后1级地上……如此类推.【规范解答】设小美上第n级楼梯有a n种上法,通过分析易知a1=1,a2=2,a4=5,a n+2=a n+1+a n,n=1,2,3,…,从而递推可得:a5=8,a6=13,a7=21,a8=34,a9=55.所以小美共有55种不同的上楼梯的方式.【借题发挥】(1)当研究对象比较复杂时,要很自然地想到从特殊到一般的思维方式.即从特殊的简单的情况人手探索变化的规律,(2)用递推过渡法计数时先要从最简单情况和特殊情况入手分析,发挥观察、归纳猜想的思想方法,最终探索出变化规律,且在探索一般的规律时,应注意抓住问题的实质为最后计数提供依据.【同类拓展】3.平面上n个圆(n为正整数),最多能把平面分成多少个部分?考点4 加法原理和乘法原理法计数例4 观察如图所示的图形:根据图(1)、(2)、(3)的规律,则图(4)中三角形的个数为_______.【切题技巧】通过观察知:图(1)中三角形的个数为:1+4=5(个);图(2)中三角形的个数为:1+4+3×4=17(个);图(3)中三角形的个数为1+4+3×4+32×4=53(个),由图(1)(2)(3)中三角形的个数的规律,可知图(4)中三角形的个数为1+4+3×4+32×4+33×4=1+4+12+36+108=161(个)【规范解答】 161个【借题发挥】(1)按本例中图(1)、(2)、(3)……的图形规律,则图(n)中三角形的个数为:1+4+3×4+32×4+33×4+…+3n-1×4(个). (2)当研究对象为比较复杂的计数问题中,我们常需要用到加法原理与乘法原理,而且还需要对研究对象进行分析,从简单情形入手,通过观察、归纳、猜想,最后找出其变化规律,再依据规律计算其个数.【同类拓展】4.一个三角形最多将平面分成两部分,两个三角形最多将平面分成8个部分,10个三角形最多将平面分成多少个部分?n个三角形呢?例5 分正方形ABCD的每条边为四等分,取分点(不包括正方形的四个顶点)为顶点可以画出多少个三角形?【切题技巧】显然构成三角形的3个顶点不可能共线,即3个顶点不可能在正方形的同一边上,故最多有2个顶点在正方形的同一边上;又因为三角形顶点只能取分点,故必须在正方形的边上.因此只有两种情况:(1)三角形的顶点分别在正方形的三边长;(2)三角形的顶点分别在正方形的两条边上.【规范解答】分两类计算:(1)第一类:如图(1)三角形的顶点分别在正方形的在三条边上.首先,从4条边中取3条有4种取法;其次从每条边上取一点,各有3种取法,故总共计有4×3×3×3=108(个)三角形.(2)第二类如图(2),三角形的两个顶点位于正方形的一条边上,而第三个顶点在正方形的另一条边上.首先,从4条边取1条有4种取法,在这边3个分点中取2点,也有3种取法;其次,从其余3边中的9点中取1点,有9种取法,故共有4×3×9=108(个)三角形.综上所述,两类合计,共有216个三角形.【借题发挥】(1)在使用加法原理和乘法原理时一定要明确两者的不同之处:在用加法原理时,完成一件事有n类方法,都能完成这件事,而用乘法原理时,完成一件事情可分为n步,只有每一步都完成了,这件事情才得以完成.(2)运用加法原理的关键在于合理适当地进行分类,使所分类既不重复又不遗漏;而运用乘法原理的关键在于分步骤,要正确地设计分步程序,使每步之间既互相联系,又彼此独立.【同类拓展】5.至少有两个数字相同的三位数共有( )个.A.280 B.180 C.252 D.396参考答案1.69个.2.9(种).3.n2-n+2(个部分).4.10个三角形最多将平面分成272个部分,n个三角形最多将平面分成(3n2-3n+2)个部分.5.C。
怎么数梯形的个数技巧四年级上册一、活动背景在四年级上册的数学课程中,学生需要掌握一些基本的图形计数方法。
梯形是一种常见的图形,在日常生活中也经常出现。
因此,如何数梯形的个数成为了一个重要的数学问题。
为了帮助学生解决这个问题,我们将介绍一些技巧和方法。
二、活动目标1. 让学生掌握数梯形个数的基本技巧和方法。
2. 培养学生的观察力和逻辑思维能力。
3. 提高学生的数学应用能力,增强学生对数学的兴趣和信心。
三、活动步骤1. 导入:教师首先向学生介绍梯形的概念和特点,并引导学生观察一些简单的梯形图片,让学生对梯形有初步的认识。
2. 技巧讲解:教师向学生介绍数梯形个数的技巧和方法。
首先,教师可以引导学生将梯形分组,每组中包含两个或两个以上的梯形。
然后,让学生按照一定的顺序(如从上到下、从左到右等)数一数每组中梯形的数量,再将各组的数量相加即可得到总数。
对于特殊的梯形(如等腰梯形、直角梯形等),教师可以引导学生根据其特点进行计数。
3. 实践操作:教师出示一些简单的梯形图片,让学生根据所学的技巧和方法进行计数。
学生可以小组合作,互相帮助,共同完成任务。
教师对学生的实践操作进行指导,纠正错误,表扬优秀。
4. 总结反馈:教师总结学生的实践操作情况,表扬优秀的学生,对不足之处进行指导。
同时,教师还可以引导学生思考其他可能存在的问题,例如图片中的梯形大小不一、重叠等情况,让学生学会灵活运用技巧和方法。
四、活动延伸1. 布置作业:让学生回家后自己数一数生活中遇到的梯形物品,如楼梯、篱笆、纸箱等,进一步巩固所学的技巧和方法。
2. 拓展活动:教师可以组织学生参加一些与梯形计数相关的数学游戏、竞赛等活动,增强学生对数学的兴趣和爱好。
五、注意事项1. 教师在讲解技巧和方法时,要注重学生的理解和掌握情况,可以适当调整讲解难度和速度。
2. 教师在实践操作中,要关注学生的操作情况,及时纠正错误,鼓励学生积极思考、勇于尝试。
3. 教师在总结反馈时,要注重学生的个体差异和特点,因材施教,让每个学生都能在活动中得到提高和进步。
图形计数知识要点1.长方形,有n 行m 列,则共有(1+2+…+m )×(1+2+…+n )个长方形。
2.正方形有n 行m 列(n>m )个小正方形,则共有m ×n +(m -1)×(n -1)+…+1×(n -m+1)个正方形。
典型例题例1 图12-1中有多少个正方形?例2 在图12-2中有多少个三角形?例3 如图12-3,平面上有12个点,可任意取其中四个点围成一个正方形,这样的正方形有多少个?例4 图12-4中共有( )个正方形。
图12-1ABC 图12-2图12-3例5 有同样大小的立方体27个,把它们竖3个,横3个,高3个,紧密地没有缝隙地搭成一个大的立方体(如图12-5)。
如果用1根很直的细铁丝扎进这个大立方体的话,最多可以穿透几个小立方体?练习题1.数一数图12-6有多少条线段?2.数一数图12-7有多少个角?3.数一数图12-8和12-9各有多少个三角形?4.数一数图12-10共有多少个长方形?5.数一数下图共有多少个正方形?6.数一数图12-12共有多少个正方形?图12-5 图12-6图12-7图12-8图12-9图12-10图12-117.数一数图12-13中有多少个三角形?8.数一数图12-14有多少个三角形?9.图12-15中共有多少个三角形?10.图12-16共有8个点,连接任意四个点围成一个长方形。
一共能围多少个长方形。
11.图12-17中共有6个点,连接其中的三个点围成一个正三角形。
一共能围成多少个正三角形?12.图12-18中共有9个点,连接其中的四个点围成一个梯形。
一共能围成多少个梯形?图12-13图12-14图12-15 图12-16 图12-17图12-1813.图12-19中共有多少个正方形(图中所有小格子都是形状与面积一样的正方形)?14.图12-20中共有多少个正方形?15.数一数图12-21中有多少个正方形。
二年级奥数:《飞速图形计数》(预热)前铺知识一、认识各种图形二、标号法(零散图形计数)数一数下图中,分别少个长方形和圆形?数的时候,长方形和圆形一定要分开计数,并且每数一个图形,都要做标记,也就是标号,这样才能做到不重复也不遗漏.如图所示,长方形有2个,圆形有6个.三、恰含法【例1】数一数下图中一共有多少个角?①②③恰含1个角的:①、②、③,共3个;恰含2个角的:①+②、②+③,共2个;恰含3个角的:①+②+③,共1个.一共:3+2+1=6(个)答:一共有6个角.【例2】数一数下图有多少个长方形?①⑤②③④恰含1个长方形的:①、②、③、④、⑤,共5个;恰含2个长方形的:①+②、②+③、③+④、④+⑤,共4个;恰含3个长方形的:②+③+④,共1个.一共:5+4+1=10(个)答:一共有10个长方形.四、其他分类方法1、按大小分类有4个小正方形,3个大正方形.2、按位置分类中间有2个圆,周围有3个圆.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《飞速图形计数》知识点精讲【知识点总结】复习1、枚举法(标号法)2、恰含法(通用)新知识一、简单规整图形(肩并肩、手拉手排成一排)开火车大法总数=火车头(基本图形数)依次加到1二、多层规整图形分层数(相合不能忘)三、不规整图形分类法:①分部分②分大小(恰含法)③分方向注:常见的【简单规整图形】(特别:数正方形不能用开火车大法)线段角【例1】数一数下面一共有多少条线段?①②③④方法1:恰含1条:4条恰含2条:①②、②③、③④3条恰含3条:①②③、②③④2条恰含4条:①②③④1条总数:4+3+2+1=10(条)方法2:基本线段有4条,所以从4开始依次加到14+3+2+1=10(条)答:一共有10条线段.【例2】数一数图中有多少个三角形?每层个数:4+3+2+1=10(个)层数:3层总数:10×3=30(个)答:一共有30个三角形.【例3】数一数右侧图形中一共有多少个三角形?左边:3+2+1=6(个)右边:3+2+1=6(个)合起来:3个总数:6+6+3=15(个)答:一共有15个三角形.【例4】数一数右侧图形中一共有多少个三角形?恰含1个:①、②、③、④、⑤、⑥6个Array恰含2个:①②、③④、⑤⑥3个恰含3个:①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②6个恰含6个:①②③④⑤⑥1个6+3+6+1=16(个)答:一共有16个三角形.【例5】数一数下面图形中一共有多少个正方形?方法:先按照正的和斜的这两个不同方向,把图形拆分出来.正的:按大小分类数,斜的:一个田字格,有5个正方形最小:4个中等大小:5个最大:1个共4+5+1=10(个)总数:10+5=15(个)答:一共有15个正方形.【学习建议】本讲讲的是数图形的方法,根据不同类型的图形有不同的巧妙方法,同学们要仔细辨认图形的种类,像是简单规整图形和多层规整图形都是有巧妙方法的;如果是不规则图形,那么一定要注意分类,分类的依据是什么,数的时候思路要清楚,这样才不会数错.《飞速图形计数》补充题1.数一数下面两幅图中分别有多少条线段?2. 在一条直线上有10个端点,那么在这条直线上可以数出多少条线段?3. 下图中有多少个三角形?4、数一数,下面有多少个长方形?5、数一数图中有多少个正方形?6、数一数下面一共有几个正方形.7、数一数,下图中包含有苹果的三角形有几个?8、数一数下图中一共有多少个平行四边形?答案解析1、(1)5+4+3+2+1=15(条)答:这幅图中有15条线段.(2)(3+2+1)+(2+1)=9(条)答:这幅图中有9条线段.2、基本线段数:10-1=9(条)总线段数:9+8+7+6+5+4+3+2+1=45(条)答:这条直线上有45条线段.3、每层个数:5+4+3+2+1=15(个)层数:3层总数:15×3=45(个)答:图中共有45个三角形.4、长边线段数:3+2+1=6(条)宽边线段数:4+3+2+1=10(条)长方形总个数:10×6=60(个)答:图中共有60个长方形.5、恰含1个:5×3=15(个)恰含4个:8个恰含9个:3个正方形总个数:15+8+3=26(个)答:图中共有26个正方形.6、按照正的和斜的两个方向,先把原图形拆分成如下两个图形.恰含1个:4×4=16(个)一个田字格有5个正方形恰含4个:3×3=9(个)恰含9个:2×2=4(个)恰含16个:1×1=1(个)共:16+9+4+1=30(个)所以一共有:30+5=35(个)正方形答:一共有35个长方形.7、按照三角形从小到大的顺序,且时刻注意题目要求,要包含苹果.恰含1个:2个恰含4个:6个恰含9个:5个恰含16个:3个最大的:1个共:2+6+5+3+1=17(个)答:含有苹果的三角形一共有17个.8、是简单规整图形,肩并肩、手拉手,可以用开火车大法.6+5+4+3+2+1=21(个)答:一共有21个平行四边形.。
二年级奥数:《飞速图形计数》(预热)前铺知识一、认识各种图形二、标号法(零散图形计数)数一数下图中,分别少个长方形和圆形?数的时候,长方形和圆形一定要分开计数,并且每数一个图形,都要做标记,也就是标号,这样才能做到不重复也不遗漏.如图所示,长方形有2个,圆形有6个.三、恰含法【例1】数一数下图中一共有多少个角?①②③恰含1个角的:①、②、③,共3个;恰含2个角的:①+②、②+③,共2个;恰含3个角的:①+②+③,共1个.一共:3+2+1=6(个)答:一共有6个角.【例2】数一数下图有多少个长方形?①⑤②③④恰含1个长方形的:①、②、③、④、⑤,共5个;恰含2个长方形的:①+②、②+③、③+④、④+⑤,共4个;恰含3个长方形的:②+③+④,共1个.一共:5+4+1=10(个)答:一共有10个长方形.四、其他分类方法1、按大小分类有4个小正方形,3个大正方形.2、按位置分类中间有2个圆,周围有3个圆.如何预习?为了保护孩子课前的好奇心和学习兴趣,以及保证课堂效果,家长在给孩子预习的时候,一定要把握好度.预习,切忌给孩子讲解书本上的例题和知识点,因为孩子容易先入为主,如果家长选取的方式方法不当,那么孩子很难转换思路了;另外,家长给孩子讲过例题后,孩子可能会觉得自己已经学会了,上课的时候就不愿意认真听了.我们预习的目的是回顾这一讲课前的铺垫知识,以及引起孩子的思考,因此家长可以把我们的这份预习资料打印出来,让孩子自己看一看,如果孩子有不明白的,您可以适当点拨.《飞速图形计数》知识点精讲【知识点总结】复习1、枚举法(标号法)2、恰含法(通用)新知识一、简单规整图形(肩并肩、手拉手排成一排)开火车大法总数=火车头(基本图形数)依次加到1二、多层规整图形分层数(相合不能忘)三、不规整图形分类法:①分部分②分大小(恰含法)③分方向注:常见的【简单规整图形】(特别:数正方形不能用开火车大法)线段角【例1】数一数下面一共有多少条线段?①②③④方法1:恰含1条:4条恰含2条:①②、②③、③④3条恰含3条:①②③、②③④2条恰含4条:①②③④1条总数:4+3+2+1=10(条)方法2:基本线段有4条,所以从4开始依次加到14+3+2+1=10(条)答:一共有10条线段.【例2】数一数图中有多少个三角形?每层个数:4+3+2+1=10(个)层数:3层总数:10×3=30(个)答:一共有30个三角形.【例3】数一数右侧图形中一共有多少个三角形?左边:3+2+1=6(个)右边:3+2+1=6(个)合起来:3个总数:6+6+3=15(个)答:一共有15个三角形.【例4】数一数右侧图形中一共有多少个三角形?恰含1个:①、②、③、④、⑤、⑥6个Array恰含2个:①②、③④、⑤⑥3个恰含3个:①②③、②③④、③④⑤、④⑤⑥、⑤⑥①、⑥①②6个恰含6个:①②③④⑤⑥1个6+3+6+1=16(个)答:一共有16个三角形.【例5】数一数下面图形中一共有多少个正方形?方法:先按照正的和斜的这两个不同方向,把图形拆分出来.正的:按大小分类数,斜的:一个田字格,有5个正方形最小:4个中等大小:5个最大:1个共4+5+1=10(个)总数:10+5=15(个)答:一共有15个正方形.【学习建议】本讲讲的是数图形的方法,根据不同类型的图形有不同的巧妙方法,同学们要仔细辨认图形的种类,像是简单规整图形和多层规整图形都是有巧妙方法的;如果是不规则图形,那么一定要注意分类,分类的依据是什么,数的时候思路要清楚,这样才不会数错.《飞速图形计数》补充题1.数一数下面两幅图中分别有多少条线段?2. 在一条直线上有10个端点,那么在这条直线上可以数出多少条线段?3. 下图中有多少个三角形?4、数一数,下面有多少个长方形?5、数一数图中有多少个正方形?6、数一数下面一共有几个正方形.7、数一数,下图中包含有苹果的三角形有几个?8、数一数下图中一共有多少个平行四边形?答案解析1、(1)5+4+3+2+1=15(条)答:这幅图中有15条线段.(2)(3+2+1)+(2+1)=9(条)答:这幅图中有9条线段.2、基本线段数:10-1=9(条)总线段数:9+8+7+6+5+4+3+2+1=45(条)答:这条直线上有45条线段.3、每层个数:5+4+3+2+1=15(个)层数:3层总数:15×3=45(个)答:图中共有45个三角形.4、长边线段数:3+2+1=6(条)宽边线段数:4+3+2+1=10(条)长方形总个数:10×6=60(个)答:图中共有60个长方形.5、恰含1个:5×3=15(个)恰含4个:8个恰含9个:3个正方形总个数:15+8+3=26(个)答:图中共有26个正方形.6、按照正的和斜的两个方向,先把原图形拆分成如下两个图形.恰含1个:4×4=16(个)一个田字格有5个正方形恰含4个:3×3=9(个)恰含9个:2×2=4(个)恰含16个:1×1=1(个)共:16+9+4+1=30(个)所以一共有:30+5=35(个)正方形答:一共有35个长方形.7、按照三角形从小到大的顺序,且时刻注意题目要求,要包含苹果.恰含1个:2个恰含4个:6个恰含9个:5个恰含16个:3个最大的:1个共:2+6+5+3+1=17(个)答:含有苹果的三角形一共有17个.8、是简单规整图形,肩并肩、手拉手,可以用开火车大法.6+5+4+3+2+1=21(个)答:一共有21个平行四边形.。
第33卷第6期2003年6月数学的实践与认识M A TH EM A T I CS I N PRA CT I CE AND TH EO R YV o l 133 N o 16 June,2003 简单图的一种计数方法徐尚进1, 吕跃进2(1.LM AM ,北京大学数学科学学院,北京 100871)(2.广西大学数学与信息科学系,南宁 530004)摘要: 对某一类图的邻接矩阵进行分类,从而给出这类图的一种计数方法,并且这种方法比较原来的Po lya 方法更为可行.关键词: 图;邻接矩阵;轨道1 引 言收稿日期:2003201219基金项目:国家自然科学基金资助项目(项目编号:10161001) n 阶简单图的计数问题是一个比较基本的问题,某些图(比如简单无向图)的计数问题在组合数学中已可以用Po lya 计数方法解决[1].但往往这些计数方法的复杂度比较大,因此寻求其他更可行的方法是有意义的.本文通过对图的邻接矩阵分类给出另一种计算复杂性比Po lya 方法要小的计数方法.一个n 阶简单图G 是指一个顶点数为n 且无环无重边的图,即顶点集V (G )={v 1,v 2,…,v n },边集E (G )ΑV (2)∶={(v i ,v j ) v i ,v j ∈V ,v i ≠v j }.通常记为G =(V ,E ).图的计数问题就是要计算某一类n 阶图中不同构的个数.而所谓同构的图是指如果另有一个图G ′=(V ′,E ′)满足:存在V 到V ′的一个双射Ρ,使(v i ,v j )∈E Ζ(v Ρi ,v Ρj )∈E ′,则称图G =(V ,E )与图G ′=(V ′,E ′)同构.显然, V ′ = V 是这两个图同构的必要条件,并且在同构意义下,图与其顶点是何元素无关,所以在本文中我们通常取V ′=V ={1,2,…,n },Ρ∈S n .于是,图G =(V ,E )与图G ′=(V ,E ′)同构当且仅当:ϖΡ∈S n ,使得(i ,j )∈E Ζ(i Ρ,j Ρ)∈E ′.2 定义与性质设8是顶点集为V ={1,2,…,n }的某一类图的全体,而#是V 上的一个置换群,即#ΦS n .任取Ρ∈#,G =(V ,E )∈8,令G Ρ=(V ,E Ρ),其中E Ρ={(i Ρ,j Ρ) (i ,j )∈E }.则根据图同构的定义,G Ρ∈8.由此可以诱导#在8上的一个作用.显然,同一轨道中的图是相互同构的.反之,如果取#=S n ,则同构的图必然同属一个轨道.于是这一类图的计数问题就是8在S n 作用下的轨道个数问题.我们已有如下著名的Burn side 引理:Burn side 引理[2] 集合8在群#作用下的轨道数N 为N =1# ∑Ρ∈#fix 8(Ρ) ,其中fix8(Ρ)={G∈8 GΡ=G},即Ρ在8中的不动点集.然而,对每一个Ρ,直接计算 fix8(Ρ) 是困难的,我们将另觅他法.定义211 记n阶(0-1)方阵的集合为M n×n(F2)(F2是2元素域),任取Ρ∈S n,则Ρ可以诱导M n×n(F2)上的一个置换:ΠA=(a ij)n×n∈M n×n(F2),定义Ρ:A →AΡ∶=(a iΡjΡ)n×n∈M n×n(F2). 如果AΡ=B,则称矩阵A与B是置换等价的,并记为A~B.定义212 记M0∶={(a ij)n×n∈M n×n(F2) a ii=0,i=1,…,n},M1∶={A∈M0 A3 =A}(A3表示A的转置矩阵).如下性质显然:性质213 ΠΡ∈S n,MΡ0ΑM0,MΡ1ΑM1,其中MΡ0∶={AΡ A∈M0},MΡ1∶={AΡ A ∈M1}.我们知道,对n个顶点的图G=(V,E),可以确定一个n阶(0-1)方阵A=(a ij)n×n ∈M n×n(F2),其中a ij=1,(i,j)∈E, 0,(i,j)|E. 通常称A为图G=(V,E)的邻接矩阵.邻接矩阵也有如下明显的性质:性质214 设G=(V,E)和G′=(V,E′)的邻接矩阵分别为A和A′,则G与G′同构当且仅当A~A′.设8是顶点集为V的某一类图的集合,由图同构定义,相应的邻接矩阵的集合M在S n 作用下是不变的.由Burn side引理,8中不同构图的个数等于M在S n作用下的轨道个数:N=1n!∑Ρ∈Snfix M(Ρ) ,其中fix M(Ρ)={A∈M AΡ=A},即Ρ在M中的不动点集.上式中,关键是对每一个Ρ∈S n,如何有效地计算 fix M(Ρ) .下一节我们将给出计算 fix M(Ρ) 的方法.3 主要结论设#ΦS n,考虑#在V(2)上的自然作用,即(i,j)Ρ∶=(iΡ,jΡ),其中i,j∈V,Ρ∈#.在这个作用下的每个轨道今后都称为#-轨道.显然,如果∃是一个#-轨道,则∃3∶= {(i,j) (j,i)∈∃}也是一个#-轨道,通常称∃3是∃的转置.如果∃3=∃,还称∃是自配对的.引理311 设Ρ∈S n,记c(Ρ)为循环群〈Ρ〉作用在V(2)上的〈Ρ〉-轨道个数,则 fix M(Ρ) =2c(Ρ).证 设∃是一个〈Ρ〉-轨道,任取A=(a ij)n×n∈fix M(Ρ).由AΡ=(a iΡjΡ)n×n.则AΡ= A]a ij=a iΡjΡ.即Π(i,j),(k,l)∈∃]a ij=a k l.但a ij的取值为0或1以及〈Ρ〉-轨道的个数是c(Ρ),于是 fix M(Ρ) =2c(Ρ).至此,如何计算V(2)中〈Ρ〉-轨道的个数是计算 fix M(Ρ) 的关键.我们先将置换Ρ分解成不相交的循环之积:46数 学 的 实 践 与 认 识33卷Ρ=(i (1)1,…,i (1)t 1)(i (2)1,…,i (2)t 2)…(i (u )1,…,i (u )t u ),(1)其中∑uk =1t k =n ,并且t k 可取1(k =1,2,…,u ).考虑Ρ的第k 个循环(i (k )1,…,i (k )t k )和第l 个循环(i (l )1,…,i (l )t l ),记V (2)k l ∶={(i ,j ) i ∈{i (k )1,…,i (k )t k },j ∈{i (l )1,…,i (l )t l },i ≠j }. 注 V(2)k l与Ρ的分解有关.显然有:V(2)=∪u k =1∪ul =1V(2)k l.(2) 引理312 1)如果k ≠l ,则V(2)k l由(t k ,t l )个〈Ρ〉-轨道组成,其中(t k ,t l )表示t k 和t l 的最大公因子;2)如果k =l ,则V(2)kk由t k -1个〈Ρ〉-轨道组成.证 1)设k ≠l 且(i ,j )∈V (2)k l .不失一般性,设(i ,j )=(i (k )1,j (l )1),则ΠΡs∈〈Ρ〉,(i ,j )Ρs=(i Ρs,j Ρs)∈V (2)k l 以及iΡtk =i ,j Ρtl =j .易知,如果h 是使i Ρh=i 和j Ρh=j 同时成立的最小正整数,则h 只能等于t k 和t l 的最小公倍数[t k ,t l ].于是,(i ,j )属于如下轨道:(i ,j )=(i (k )1,j (l )1),(i (k )2,j (l )2),…,(i (k )r ,j (l )r ),…,(i (k )h ,j (l )h )}.(3) 其中r Φh .如果r (或h )大于t k (或t l ),则作为下标时将按相应的模取值.今后也这样处理下标,仅此说明.事实上,轨道(3)中的各元素彼此不同,说明轨道的长即为h =[t k ,t l ].显然它与(i ,j )的选取无关,说明V(2)k l中〈Ρ〉-轨道的长都等于h =[t k ,t l ].而当k ≠l 时,V (2)k l 中共有t k ×t l 个元素,所以V(2)k l中〈Ρ〉-轨道的个数是:t k t l[t k ,t l ]=(t k ,t l ). 2)同(1),V (2)kk 中〈Ρ〉-轨道的长也等于[t k ,t k ]=t k .但V (2)kk 中只有t k (t k -1)个元素(因为对角线上的t k 个元素不计),所以(2)成立.定理313 设Ρ∈S n 且Ρ的分解如(1)式,则1)V{2}上的〈Ρ〉-轨道个数c (Ρ)=2 ∑k <l(t k ,t l )+n -u ;2) fix M 0(Ρ) =4∑k <l(t k ,t l )×2n -u .证 1)根据引理312和公式(2),即得V (2)中的〈Ρ〉-轨道个数c (Ρ)=∑ul =1∑uk ≠l(t k,t l)+∑uk =1(tk-1)=2∑k <l(t k,t l)+n -u . 2)由引理311和(1)直接得.然而计算 fix M 1(Ρ) 稍复杂,因为M 1中的矩阵除对角线为0外还对称,所以不能直接按定理313(2)来计算 fix M 1(Ρ) .设A =(a ij )n ×n ∈fix M 1(Ρ),∃是V (2)中一个非自配对的〈Ρ〉-轨道,则Π(i ,j )∈∃,都有a ij =a j i ,而(j ,i )∈∃3≠∃.说明A 中下标属于∃3的元素不能独立取值.于是在计算 fix M 1(Ρ) 时∃与∃3应作为一个轨道考虑.为此,还需要有关自配对轨道的一些结论:566期徐尚进等:简单图的一种计数方法引理314 设#ΦS n且∃是一个#-轨道,如果ϖi,j使得(i,j),(j,i)∈∃.则∃是自配对的.证 Π(r,s)∈∃,ϖΡ,Ρ1∈#使得(r,s)Ρ=(i,j),(i,j)Ρ1=(j,i),则(r,s)ΡΡ1Ρ-1=(i,j)Ρ1Ρ-1=(j,i)Ρ-1=(s,r)∈∃.引理315 设k≠l,则1)V(2)k l中没有自配对的〈Ρ〉-轨道;2)V(2)k l中所有〈Ρ〉-轨道的转置都在V(2)lk中.引理316 1)k≠l]{i(k)1,…,i(k)tk }∩{i(l)1,…,i(l)tl}=<,所以(1)成立;2)显然.引理316 1)如果t k是偶数,则V(2)kk中有且只有一个自配对的〈Ρ〉-轨道;2)如果t k是奇数,则V(2)kk中没有自配对的〈Ρ〉-轨道.证 1)不失一般性,设Ρ的第k个循环(i(k)1,…,i(k)tk)为(1,2,…,t k),即V(2)kk={(i,j) i,j=1,…,t k,i≠j}.设∃={(i,j)∈V(2)kk i-j =t k2}.往证∃是V(2)kk中唯一的自配对〈Ρ〉-轨道.首先,Π(i,j)∈∃.不妨设i<j.如果j<t k,则(i,j)Ρ=(i+1,j+1)∈∃;如果j=t k,只能i=t k2,即j+1≡1(m od t k),仍有(i,j)Ρ=(i+1,1)=(t k2+1,1)∈∃.总之,∃Ρ=∃.其次,由(1,t k2+1)∈∃,Π(i,j)∈∃,有(1,t k2+1)Ρi-1=(i,t k2+i).由 i-j=t k2]j≡t k2+i(m od t k)](i,t k2+i)=(i,j)]〈Ρ〉作用在∃上是传递的,说明∃的确是V(2)kk中的一个〈Ρ〉-轨道.而由它的定义直接知它是自配对的.第三,如果∃1是V(2)kk中另一个自配对的〈Ρ〉-轨道,则Π(i,j)∈∃1,ϖr<t k使得(i,j)Ρr=(j,i)∈∃1](i,j)Ρ2r=(i,j)]2r≡0(m od t k)]r=t k2]iΡt k2=j] i-j = t k2](i,j)∈∃]∃1=∃.综之,(1)成立.2)假设∃是V(2)kk中一个自配对的〈Ρ〉-轨道,则Π(i,j),(j,i)∈∃及ϖr,0<r< t k使得(i,j)Ρr=(j,i)]2r≡0(m od t k).但t k是奇数,只能r=0,矛盾.所以,(2)也成立.定理317 设Ρ∈S n且Ρ的分解如(1)式,则fix M1(Ρ) =2∑k<l(tk,t l)+∑uk=1[t k2],其中t k2表示t k的整数部分.证 先分两种情况来计算V(2)k l中非自配对的〈Ρ〉-轨道个数:(i)k≠l.根据引理312(1)和315(1),V(2)k l中都是非自配对的〈Ρ〉-轨道,共有(t k,t l)个;(ii)k=l.根据引理312(2)和316,V(2)kk包含t k-1个〈Ρ〉-轨道且根据t k的奇偶性共66数 学 的 实 践 与 认 识33卷有2[t k2]-t k+1个是自配对的,有2(t k-1-[t k2])个是非自配对的.于是V(2)中所有非自配对的〈Ρ〉-轨道数目是∑u l=1∑uk≠l(t k,t l)+∑uk=12(t k-1-[t k2]). 而所有自配对的〈Ρ〉-轨道数目是∑u k=1(2[t k2]-t k+1). 最后仍由引理311计算 fix M1(Ρ) ,但计算时非自配对的〈Ρ〉-轨道数目要除以2,于是得fix M1(Ρ) =2∑k<l(tk,t l)+∑uk=1[t k2]. 在不至于混淆的情况下,仍用c(Ρ)表示V{2}中〈Ρ〉-轨道在所有非自配对与它们的转置一一合并后新的数目,则推论318c(Ρ)=∑k<l (t k,t l)+∑uk=1[t k2]. 定理313(2)与定理317表明, fix M(Ρ) (M=M0或M1)的值完全由置换Ρ按(1)式分解后各循环节长度所确定.为方便表示,我们将置换Ρ的各循环节的长简记为乘幂形式,即t1t2…t u,并称为置换Ρ的型.在置换群理论中,两个置换同型当且仅当它们在S n中共轭.于是S n中共轭类个数等于彼此不同型置换的个数,而与Ρ同型的置换(也包括Ρ自己)个数即为Ρ在S n中共轭类的长,今后记为l(Ρ).从而有:引理319 l(Ρ)=[S n:C Sn (Ρ)],其中C Sn(Ρ)是Ρ在S n中的中心化子.事实上,S n中与Ρ同型的置换个数还有如下算法:引理3110[1] S n中型为t r11t r22…t r v v(t1>t2>…>t v,r1t1+r2t2+…+r v t v=n)的置换个数为:l(Ρ)=n!r1!r2!…r v!t r11t r22…t r v v. 引理3111 S n中不同的型的个数等于如下关于x1,…,x n的n元线性方程的非负整数解的个数:nx1+(n-1)x2+…+1x n=nx1Ε0, x2Ε0,…,x nΕ0.4 应 用综合前边的结论,我们得到如下轨道公式:轨道公式 设C为S n的共轭类集,M=M0或M1,则根据Burn side引理,M在S n作用下的轨道个数为:N=1n!∑Ρ∈Cl(Ρ)2c(Ρ),其中c(Ρ)按定理313或推论318计算.766期徐尚进等:简单图的一种计数方法以下我们将利用轨道公式来计算某一类n阶图的不同构个数.411 简单有向图的计数邻接矩阵属于M0的图称简单有向图.例411 不同构的4阶简单有向图共有218个.解 首先,由4=3+1=2+2=2+1+1=1+1+1+1知S4中置换的型为: 4,31,22,212,14.其次,由引理3110与定理313(2),得到关于l(Ρ)和c(Ρ)的表如下:C4312221214l(Ρ)68361c(Ρ)346712第三,由轨道公式,有:N=124(6×23+8×24+3×26+6×27+1×212)=218.412 简单图的计数邻接矩阵属于M1的图称简单图.例412 不同构的4阶简单图共有11个.解 首先,由4=3+1=2+2=2+1+1=1+1+1+1知S4中置换的型为: 4,31,22,212,14.其次,由引理3110与推论318,得到关于l(Ρ)和c(Ρ)的表如下:C4312221214l(Ρ)68361c(Ρ)22446第三,由轨道公式,有:N=124(6×22+8×22+3×24+6×24+1×26)=11.5 最后的说明在组合数学中(如[1]),n个顶点的简单图的计数问题也可以通过S n的轮换指标来计算,即N=P Sn (2,2,…,2n). 但由于P Sn(x1,x2,…,x n)是S n关于V(2)的轮换指标,故当n较大时将难以计算.参考文献:[1] 李宇寰.组合数学[M].北京:北京师范大学出版社.[2] 胡冠章.组合计数的群论与计算机方法[J].数学进展,1997,1:1—12.86数 学 的 实 践 与 认 识33卷A Com bi nator ic M ethod For The Si m ple GraphsXU Shang 2jin 1, LU Yue 2jin2(1.LM AM &Schoo l of M athem atical Sciences ,Pek ing U n iversity ,Beijing 100871,Ch ina )(2.D ep t .of M athem atics and Info rm ati on Science ,Guangx iU n iversity ,N ann ing 530004,Ch ina )Abstract : A com b inato ric m ethod w h ich coun ts the num ber of non 2isomo rph ic si m p le graph s is ob tained by classifying their connecti on m atrices .T he m ethod here is mo re efficien t than Po lya ′s .Keywords : graph ;connecti on m atrix ;o rb it信息为答谢广大订户多年来对本刊的支持与厚爱,《中国数学文摘》2003年对订阅全年刊物的订户赠送《中国数学文献数据库》光盘(1992—2003版).该光盘不仅囊括了1992年至2003年12年间《中国数学文摘》的全部内容,还包含了12年中未被收入《中国数学文摘》杂志中的数学文献的文摘万余条,共约9万条文献的文摘.用户界面友好,检索方便快捷!《中国数学文摘》2003年全年定价408元,每期68元.欢迎订阅!有需求者可按下列方式与我们联系.邮 编:100080通信地址:北京中关村北四环西路33号《中国数学文摘》编辑部电子信箱:m athab @m ail .las .ac .cn电 话:(010)82620643或(010)82626611-6616966期徐尚进等:简单图的一种计数方法。