刚体的平面运动1答案
- 格式:pdf
- 大小:99.03 KB
- 文档页数:2


理论力学课后习题答案-第6章--刚体的平面运动分析第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕc o s )(r R x A += (1) ϕsin )(r R y A+= (2)α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ= (3) 起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R =ϕθr R =, ϕϕrrR A+=(4) 将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R tr R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角θ 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB习题6-1图A BCv 0hθ 习题6-2图 P ωAv CA BC v oh θ 习题6-2解图为6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系?设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:Rv R v A A ==ωRv R v B B 22==ωB A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度ω=12 rad/s ,θ=30︒,ϕ=60︒,BC =270mm 。
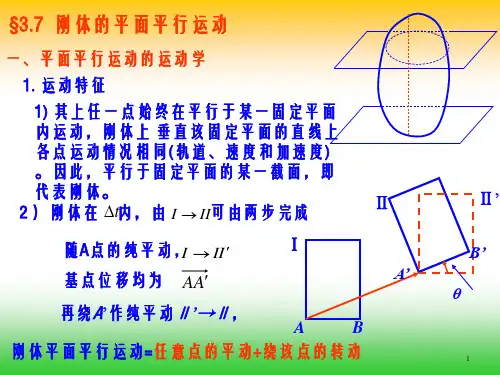


刚体的平面运动作业参考答案1.图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以等角加速度α 绕O 轴转动,当运动开始时,角速度ω0=0,转角ϕ0=0,求动齿轮以中心A 为基点的平面运动方程。
答案: 2A 22)(21, 2sin)( , 2cos )(t r R rt r R y t r R x A A αϕαα+=+=+=2. 图示平面机构中,曲柄OA =R ,以角速度ω 绕O 轴转动。
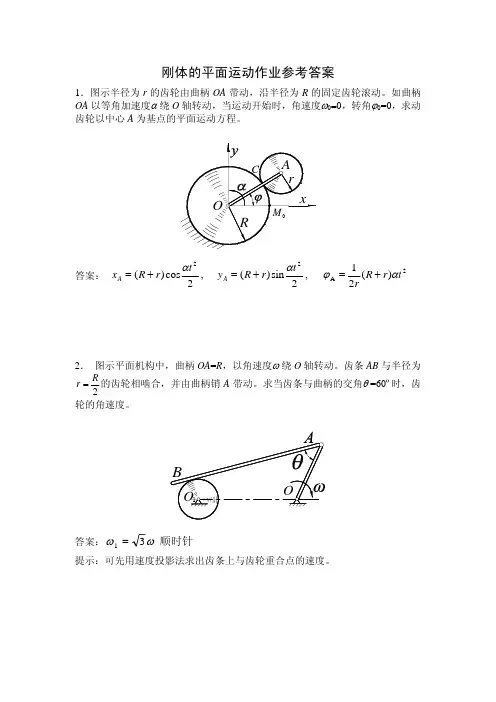
齿条AB 与半径为2Rr =的齿轮相啮合,并由曲柄销A 带动。
求当齿条与曲柄的交角θ =60º时,齿轮的角速度。
答案:顺时针 31ωω=提示:可先用速度投影法求出齿条上与齿轮重合点的速度。
3.图中曲柄OA 长150mm ,连杆AB 长200mm ,BD 长300mm 。
设OA ⊥OO 1时,AB ⊥OA ,θ =60º,曲柄OA 的角速度为4rad/s ;求此时机构中点B 和D 的速度以及杆AB 、O 1B 和BD 的角速度。
答案:逆时针顺时针顺时针 rad/s 34 , rad/s 4, rad/s 3 , mm/s 800 , mm/s 34001O =====BD B AB D B v v ωωω提示:在图示瞬时,杆AB 的速度瞬心为点C ,杆BD 的速度瞬心为点E 。
4.图示平面机构中,曲柄长OA =r ,以角速度ω0绕O 轴转动。
某瞬时,摇杆O 1N 在水平位置,而连杆NK 和曲柄OA 在铅垂位置。
连杆上有一点D ,其位置为DK =31NK ,求D 点的速度。
答案:←=320ωr v D 提示:在图示瞬时,杆AB 瞬时平动,杆KN 的速度瞬心为点N 。
5.杆AB 长0.4m ,其端点B 沿与水平成倾角θ =30º的斜面运动,而端点A 沿半径OA =0.6m 的圆弧运动,如图所示。
求当杆AB 水平时,端点B 的速度和加速度。
假设此时OA ⊥AB ,杆OA 的角速度为πrad/s ,角加速度为零。
5、刚体的平面运动5.1内容提要刚体在运动过程中,其上任一点到某一固定面间的距离保持不变,这种运动称为刚体的平面运动。
5.1.1平面图形内各点的速度平面图形内各点的速度的三种求法如表5-1所示。
通常,瞬心法和投影法应用较多。
瞬心法的关键是确定平面图形在每一瞬时的瞬心位置,表5-2给出了按已知运动条件确定平面图形瞬心位置的几种方法。
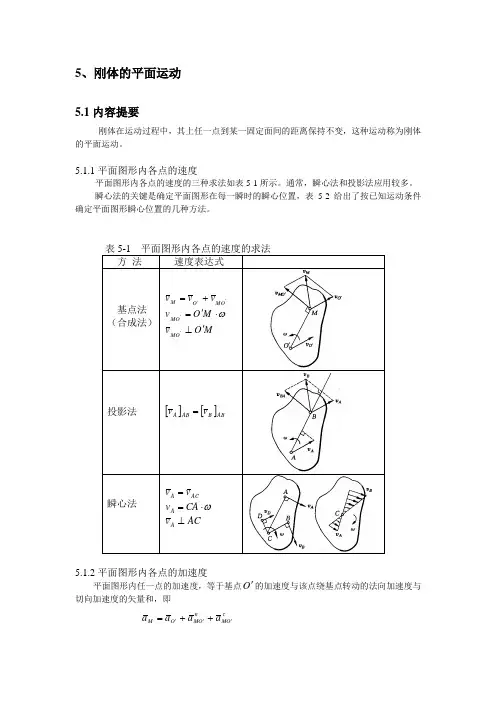
表5-1 平面图形内各点的速度的求法方 法 速度表达式基点法 (合成法)‘,MO O M v v v += ω⋅'=M O v MO ’ M O v MO '⊥‘投影法[][]AB B AB A v v =瞬心法AC A v v =ω⋅=CA v A AC v A ⊥5.1.2平面图形内各点的加速度平面图形内任一点的加速度,等于基点O '的加速度与该点绕基点转动的法向加速度与切向加速度的矢量和,即τO M n O M O M a a a a '''++=式中,2ω⋅'='O M a n O M ,方向由点M 指向基点O ';ατ⋅'='O M a O M ,方向垂直于O M ',且指向与α一致。
表5-2 几种常见情况的速度瞬心确定方法刚体运动情况瞬心位置 说明 刚体运动情况瞬心位置说明 轮沿固定面纯滚动瞬心在轮与固定面的接触处 两点速度平行且垂直于两点的连线瞬心位于两点的连线与两速度矢端连线的交点处 已知平面上任意两点速度的方位瞬心在两点速度垂线的交点上 两点速度平行且不垂直于两点的 连线瞬心位于无穷远处,该瞬时,角速度为零,各点速度相等,这种情况称为瞬时平动5.2解题要点5.2.1习题类型刚体平面运动的习题,从运动构件看,有杆和轮子的单独平面运动,以及由它们通过连接点(铰结点或接触点)所组成的平面机构。
从分析方法分,有单纯的平面运动分析,还有刚体的平面运动和点的合成运动的综合分析。

运动学部分复习题一、是非题(正确用√,错误用×,填入括号内。
)1、对于平移刚体,任一瞬时,各点速度大小相等而方向可以不同。
(×)2、在刚体运动过程中,若刚体内任一平面始终与某固定平面平行,则这种运动就是刚体的平面运动。
(× )3. 在自然坐标系中,如果速度v = 常数,则加速度a = 0。
(×) 4、点的法向加速度与速度大小的改变率无关。
( √ )5、如果知道定轴转动刚体上某一点的法向加速度,就可确定刚体转动角速度的大小和转向。
(× )6、平移刚体上各点的运动轨迹一定是直线。
(× )7、若动点相对动系的轨迹是直线,动系相对静系的运动是直线平动,则动点的绝对运动也一定是直线运动。
(×)8、在研究点的合成运动时,所选动点必须相对地球有运动(√)9、若动系的牵连运动为定轴转动,则肯定存在哥氏加速度C a。
(× ) 10、速度瞬心的速度为零,加速度也为零。
( × )11、基点法中平面图形绕基点转动的角速度与瞬心法中平面图形绕瞬心转动的角速度相同。
(√)二、选择题(请将正确答案的序号填入括号内。
)1、已知一动点作圆周运动,且其法向加速度越来越大,则该点运动的速度( A ) 。
A)越来越大; B)越来越小; C)保持不变; D)无法确定。
2、点的加速度在副法线轴上的投影( B )。
A)可能为零; B)一定为零; C)保持不变; D)无法确定。
3、动点的运动方程以弧坐标表示为)(t f s =,且沿坐标轴正向运动,但越来越慢,则 (D )。
(A)0<dt ds , 022<dt s d ; (B)0>dt ds, 022>dts d ;(C)0<dt ds , 022>dt s d ; (D)0>dt ds, 022<dts d 。
4、一绳缠绕在轮上,绳端系一重物,其以速度v 和加速度a向下运动,则绳上两点A 、D 和轮缘上两点B 、C 的速度、加速度之间关系为( D )。
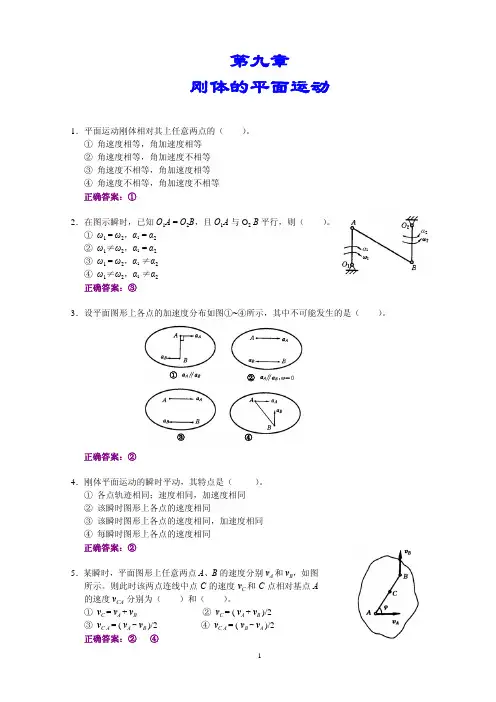
第九章刚体的平面运动1.平面运动刚体相对其上任意两点的( )。
① 角速度相等,角加速度相等② 角速度相等,角加速度不相等③ 角速度不相等,角加速度相等④ 角速度不相等,角加速度不相等正确答案:①2.在图示瞬时,已知O 1A = O 2B ,且O 1A 与O 2 B 平行,则( )。
① ω1 = ω2,α1 = α2② ω1≠ω2,α1 = α2③ ω1 = ω2,α1 ≠α2④ ω1≠ω2,α1 ≠α2正确答案:③3.设平面图形上各点的加速度分布如图①~④所示,其中不可能发生的是( )。
正确答案:②4.刚体平面运动的瞬时平动,其特点是( )。
① 各点轨迹相同;速度相同,加速度相同② 该瞬时图形上各点的速度相同③ 该瞬时图形上各点的速度相同,加速度相同④ 每瞬时图形上各点的速度相同正确答案:②5.某瞬时,平面图形上任意两点A 、B 的速度分别v A 和v B ,如图所示。
则此时该两点连线中点C 的速度v C 和C 点相对基点A的速度v CA 分别为( )和( )。
① v C = v A + v B ② v C = ( v A + v B )/2③ v C A = ( v A - v B )/2 ④ v C A = ( v B - v A )/2正确答案:② ④α1α2 ①②③④6.平面图形上任意两点A 、B 的加速度a A 、a B 与连线AB 垂直,且a A ≠ a B ,则该瞬时,平面图形的角速度ω和角加速度α应为( )。
① ω≠0,α ≠0② ω≠0,α = 0③ ω = 0,α ≠0④ ω = 0,α = 0正确答案:③7.平面机构在图示位置时,AB 杆水平,OA 杆鉛直。
若B 点的速度v B ≠0,加速度τB a = 0,则此瞬时OA 杆的角速度ω和角加速度α为( )。
① ω = 0,α ≠0② ω≠0,α = 0③ ω = 0,α = 0④ ω≠0,α ≠0正确答案:②8.在图示三种运动情况下,平面运动刚体的速度瞬心:(a )为( );(b )为( );(c )为( )。


刚体的基本运动8-2 搅拌机构如图所示,已知O1A=O2B=R,O1O2=AB,杆O1A以不变转速n rpm转动。
试分析构件BAM上M点的轨迹及其速度和加速度。
解:搅拌机构BAM作平动,故:速度和加速度方向如图所示。
刚体的平面运动10-3 两齿条以速度v1和v2同向直线平动,两齿条间夹一半径为 r 的齿轮;求齿轮的角速度及其中心O的速度。
解:(1) 齿轮作平面运动,取中心O为基点,假设齿轮转动的角速度为;(2) 齿轮A点和B点的速度是解方程得:10-4图示曲柄连杆机构中,曲柄OA = 40 cm,连杆AB = 100 cm,曲柄以转速n = 180 rpm绕O轴匀速转动。
求当φ = 45o时连杆AB的角速度及其中点M的速度。
解:(1) 连杆AB作平面运动,选A点为基点,B点的速度为已知应用正弦定理(2) M点的速度应用余弦定理注:本题也可以用速度瞬心法求连杆AB的角速度和M点的速度。
根据vA和vB得到AB杆的速度瞬心C;AB杆的角速度:M点的速度:10-5图示四连杆机构中,OA = O1B = 1/2AB,曲柄以角速度ω=3 rad/s绕O 轴转动;求在图示位置时杆AB和杆O1B的角速度。
解:(1) 分析运动:OA和O1B作定轴转动,AB作平面运动。
根据vA和vB得到AB杆的速度瞬心是O点;(2) AB杆的角速度:(3) B点的速度(4) O1B杆的角速度:注1:本题也可以用基点法求B点的速度,再求O1B杆的角速度。
以A为基点,B点的速度和O1B的角速度是:注2:本题还可以用速度投影法求B点的速度,再求O1B杆的角速度。
10-6图示曲柄摇块机构中,曲柄OA 以角速度ω0绕O轴转动,带动连杆AC在摇块B内滑动,摇块及与其刚连的BD杆则绕B铰转动,杆BD长l;求在图示位置时摇块的角速度及D点的速度。
解:(1) 分析运动:OA和BD作定轴转动,AC作平面运动。
根据vA和vB得到AC杆的速度瞬心是P点;(2) AC杆的角速度:(3) BD杆的角速度与AC杆的角速度相等,由此得到D点的速度;注:本题也可以用基点法求AC杆的角速度。
刚体平面运动一、是非题(正确或是用√,错误或否用×,填入括号内。
)1. 刚体的平动和定轴转动均是刚体平面运动的特例。
( √ )2. 刚体作瞬时平动时,刚体的角速度和角加速度在该瞬时一定都等于零。
( × )3. 轮子作平面运动时,如轮上与地面接触点C 的速度不等于零,即相对地面有滑动,则此时轮子一定不存在瞬时速度中心。
( × )4. 若在作平面运动的刚体上选择不同的点作为基点时,则刚体绕不同基点转动的角速度是不同的。
( × )5. 某刚体作平面运动,若A 和B 是其平面图形上的任意两点,则速度投影定理[][]AB B AB A v v =永远成立。
( √ )6. 作平面运动的刚体,某瞬时若角速度、角加速度同时为零,则此时刚体上各点的速度与加速度均相等。
( √ )7. 接上题,在上述条件下,有结论:刚体作平动。
( × )8. 设A 为平面运动刚体上的任意一点,I 为刚体在某时刻的速度瞬心,则A 点的运动轨迹在此处的曲率半径等于A 、I 间的距离。
( × )9. 我们知道,作平面运动的刚体上任意两点A 、B 之间有相对速度,因此,如果将一坐标系固定在此刚体上,在此坐标系中所观察到的A 、B 点之速度一般来说不相等。
( × )10. 刚体作平面运动时,若某瞬时其上有二点加速度相同,则此瞬时刚体上各点的速度都相同。
( √ )11. 平面图形上任意两点的速度在任一直线上的投影始终相等。
( × )12. 平面图形瞬时平动时,其上任意两点的加速度在这两点连线上的投影相等。
( √ )13. 刚体平动必为刚体平面运动的特例,但刚体定轴转动不一定是刚体平面运动的特例。
( × )14. 请判断下述说法是否正确:A. 刚体的平动是平面运动的特殊情况。
( × )B. 刚体的平面运动是平动的特殊情况。
( × )C. 刚体的定轴转动是平面运动的特殊情况。
第一章静力学公理与受力分析(1)一.是非题1、加减平衡力系公理不但适用于刚体,还适用于变形体。
()2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
()3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
()4、凡是受两个力作用的刚体都是二力构件。
()5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
()二.选择题1、在下述公理、法则、原理中,只适于刚体的有()①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A )b(杆ABd(杆AB、CD、整体)c(杆AB、CD、整体)精选)e(杆AC、CB、整体)f(杆AC、CD、整体四.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章静力学公理与受力分析(2)一.画出下列图中指定物体受力图。
未画重力的物体不计自重,所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WA DBCEOriginal FigureADBCEWWF AxF Ay F BFBD of the entire frame )a(杆AB、BC、整体)b(杆AB、BC、轮E、整体)c(杆AB、CD、整体)d(杆BC带铰、杆AC、整体精选)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一.是非题1、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
()2、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
()3、力偶矩就是力偶。
()二.电动机重P=500N,放在水平梁AC的中央,如图所示。
第8章刚体的平面运动一、选择题1.图8-1所示平面图形上A、B两点的加速度与其连线垂直且ɑA≠ɑB,则此瞬时平面图形的角速度ω、角加速度α应该是()。
A.ω≠0,α=0B.ω=0,α≠0C.ω=0,α=0D.ω≠0,α≠0图8-1【答案】B2.图8-2所示各平面图形的速度分布为:(a)v A=-v B,v A不垂直AB,这种速度分布是()。
A.可能的B.不可能的不垂直AB,,这种速度分布是()。
A.可能的B.不可能的图8-2【答案】B;B3.在图8-3所示机构中,则ω1()ω2。
A.=B.>C.<图8-3【答案】C4.在图8-4所示机构的几种运动情况下,平面运动刚体的速度瞬心为:(a)();(b)();(c)();(d)()。
A.无穷远处B.B点C.A、B两点速度垂线的交点D.A点E.C点图8-4【答案】D;B;A;C5.已知图8-5所示平面图形上B点的速度v B,若以A为基点,并欲使是B点相对于A点的速度,则A点的速度v A()。
A.与AB垂直B.沿AB方向,且由A指向BC.沿AB方向,且由B指向AD.与AB成φ角图8-5【答案】B二、填空题1.边长为L的等边三角形板在其自身平面内运动,已知B点的速度大小为,方向沿CB,A点的速度沿AC方向。
如图8-6所示,则此时三角板的角速度大小为______;C点的速度大小为______。
图8-6【答案】2.已知作平面运动的平面图形上A点的速度v A,方向如图8-7所示。
则B点所有可能速度中最小速度的大小为______,方向______。
【答案】;沿AB方向图8-73.已知作平面运动的平面图形(未画出)上某瞬时A点的速度大小为v A,方向如图8-8所示,B点的速度方位沿mn,AB=l,则该瞬时刚体的角速度ω为______,转向为______。
【答案】;顺时针图8-8三、判断题1.作平面运动的平面图形上(瞬时平移除外),每一瞬时都存在一个速度瞬心。
()【答案】对2.研究平面运动图形上各点的速度和加速度时,基点只能是该图形上或其延展面上的点,而不能是其他图形(刚体)上的点。
理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以匀角加速度a 绕O 轴转动,且当运动开始时,角速度00=w ,转角0=j 。
求动齿轮以中心A为基点的平面运动方程。
解:图示,A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2,故有 ∠CAC 2=r R /j ,所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ,N 用铰C 连结,作平面平行运动。
已知AC=BC=600mm ,在题附图所示位置s mm v s mm v B A /100,/200==,方向如图所示。
试求C 点的速度。
解:由速度投影定理得()()0==BC C BC B v v 。
则v C 必垂直于BC 连线,v C 与AC 连线的夹角为30°。
由()()AC A AC C v v = 即得:s mm v v A C /200== ,方向如题4-6附图示。
解毕。
8-9 图所示为一曲柄机构,曲柄OA 可绕O 轴转动,带动杆AC 在套管B 内滑动,套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。
已知:OA =BD =300mm ,OB =400mm ,当OA 转至铅直位置时,其角速度ωo =2rad/s ,试求D 点的速度。
C 12Aj C解 (1)平面运动方法: 由题可知:BD AC w w =确定AC 杆平面运动的速度瞬心。
套筒中AC 杆上一点速度沿套筒(为什么?)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析?关键求AC 杆角加速度(=BD 杆角速度) 基点法,分析AC 杆上在套筒内的点(B’):(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小:× ∠ ∠ × 方位:× ∠ ∠ ∠ 再利用合成运动方法:动点:套筒内AC 杆上的点B’,动系:套筒。
6-1在图示四连杆机构中,已知:匀角速度O ω,OA =B O 1=r 。
试求在°=45ϕ且AB ⊥B O 1的图示瞬时,连杆AB 的角速度AB ω及B 点的速度。
解:连杆AB 作平面运动,由基点法得BA A B v v v +=由速度合成的矢量关系,知φcos v A BA =v杆AB 的角速度)(/AB /O BA AB 2122+==ωωv (逆时针)B 点的速度2245/r cos v O A B ω=°=v (方向沿AB )6-2. 在图示四连杆机构中,已知:3.021===L B O OA m ,匀角速度2=ωrad/s 。
在图示瞬时,11==L OB m ,且杆OA 铅直、B O 1水平。
试求该瞬时杆B O 1的角速度和角加速度。
解:一.求1ω60230..OA v A =×=⋅=ω m/s取A 为基点,则有BA A B v v v += 得 23.0/6.0ctg v v A B ===ϕ m/sm09.2)3.01()3.0/6.0(sin /v v 2/122A BA =+×==ϕ杆B O 1的角速度67630211../BO /v B ===ω rad/s 顺时针 二.求1ε取点A 为基点,则有n BA A a a a a a ++=+ττBA nB B将上式向X 轴投影21222857s /m .B O /ctg v )sin AB /v (OA ctg a )sin /a (a a a sin a cos a sin a BBA n B n BA A B nBA A n B B +=⋅+⋅+⋅−=++−=−=+−ϕϕωϕϕϕϕϕττ杆B O 1的角加速度7.1923.0/8.57/11===B O a B τεrad/s 2逆时针6-3.图示机构中,已知:OA =0.1m , DE =0.1m ,m 31.0=EF ,D 距OB 线为h=0.1m ;rad 4=OA ω。
刚体的平面运动作业1参考答案
1.图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以等角加速度α 绕O 轴转动,当运动开始时,角速度ω0=0,转角ϕ0=0,求动齿轮以中心A 为基点的平面运动方程。
答案: 2A 2
2
)(21
, 2
sin
)( , 2
cos )(t r R r
t r R y t r R x A A αϕαα+=
+=+=
2. 图示平面机构中,曲柄OA =R ,以角速度ω 绕O 轴转动。
齿条AB 与半径为
2
R
r =的齿轮相啮合,并由曲柄销A 带动。
求当齿条与曲柄的交角θ =60º时,齿
轮的角速度。
答案:顺时针 31ωω=
提示:可先用速度投影法求出齿条上与齿轮重合点的速度。
3.图中曲柄OA 长150mm ,连杆AB 长200mm ,BD 长300mm 。
设OA ⊥OO 1时,AB ⊥OA ,θ =60º,曲柄OA 的角速度为4rad/s ;求此时机构中点B 和D 的速度以及杆AB 、O 1B 和BD 的角速度。
答案:
逆时针
顺时针顺时针 rad/s 3
4 , rad/s 4
, rad/s 3 , mm/s 800 , mm/s 34001
O =====BD B AB D B v v ωωω
提示:在图示瞬时,杆AB 的速度瞬心为点C ,杆BD 的速度瞬心为点E 。
4.图示平面机构中,曲柄长OA =r ,以角速度ω0绕O 轴转动。
某瞬时,摇杆O 1N 在水平位置,而连杆NK 和曲柄OA 在铅垂位置。
连杆上有一点D ,其位置为
DK =31
NK ,求D 点的速度。
答案:←=
3
2
0ωr v D 提示:在图示瞬时,杆AB 瞬时平动,杆KN 的速度瞬心为点N 。