巧算五角星的面积

几何中的五芒星构造五芒星，又称为五角星，是一种常见的几何形状。

在几何中，有几种方法可以构造五芒星，本文将介绍其中三种常用的方法。

方法一：正五角形构造法正五角形是一种具有五个边相等，五个内角相等的几何形状。

我们可以通过正五角形的构造来进一步得到五芒星。

步骤一：画出一个正五角形ABCED，其中A为顶点。

步骤二：以点A为圆心，AB为半径，画一个圆。

步骤三：以点C为圆心，CA为半径，画一个圆。

步骤四：圆A和圆C的交点分别为F和G，在线段FG上再画一个点H。

步骤五：连接线段AF、AH、HD、DE、EA，即可得到五芒星。

方法二：黄金分割法黄金分割法是一种利用黄金分割比例构造五芒星的方法。

步骤一：画一个正五边形ABCDE。

步骤二：以线段AB的中点F为圆心，以线段BC的长度为半径，画一个圆。

步骤三：以线段BC的中点G为圆心，以线段AB的长度为半径，画一个圆。

步骤四：圆F和圆G的交点分别为H和I，在线段HI上再画一个点J。

步骤五：连接线段AJ、BJ、CJ、DJ、EJ，即可得到五芒星。

方法三：旋转法旋转法是一种以正五边形为基础，通过对正五边形的旋转来得到五芒星的构造方法。

步骤一：画一个正五边形ABCDE。

步骤二：以点A为中心，将正五边形顺时针旋转72度（或逆时针旋转108度）得到一个新的五边形，连接线段AB、BC、CD、DE、EA。

步骤三：重复步骤二，每次旋转72度（或逆时针旋转108度），直到完成五个重合的五边形。

步骤四：连接五个五边形的顶点，即可得到五芒星。

这三种方法可以用来构造五芒星，每一种方法都有其独特的特点和美感。

几何中的五芒星构造是一项有趣且富有挑战性的几何问题，希望本文的介绍能对你有所帮助。

第四讲 巧算面积计算长方形、正方形的面积，知道长方形的面积=长×宽，正方形的面积=边长×边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例如，对左以下图，我们无法直接求出它的面积，但是通过将它分割成几块，其中每一块都是正方形或长方形(见右以下图)，分别计算出各块面积再求和，就得出整个图形的面积。

例1 把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米？举一反三 将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形，那么剪下的另一个小长方形的面积是多少？例2 求下面图形的面积。

〔单位：厘米〕1324举一反三 计算下面图形的面积。

〔单位：厘米〕(1)15203040 (2)31122例3 有两个相同的长方形，长是8厘米，宽是3厘米。

如果把它们按以下图叠放，这个图形的面积是多少？举一反三求以下图中阴影部分的面积。

〔单位：分米〕例4 一个长方形假设长增加2厘米，面积就增加10平方厘米，假设宽减少3厘米，面积就减少18平方厘米。

求原来长方形的面积。

3举一反三一个长方形，假设长减少5厘米，面积就减少50平方厘米，假设宽增加7厘米，面积就增加28平方厘米。

原来长方形的面积是多少平方厘米？例5 右图为一个长50米、宽25米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖(阴影部分)。

求游泳池面积和地砖面积。

举一反三有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？例6 一个边长为10米的正方形花坛，依次连接四边中点得到一个小正方形的喷泉，求小正方形喷泉的面积。

例7 一个长方形，如果宽增加2厘米，或长增加3厘米，他们的面积都增加120平方厘米，原来长方形的面积是多少？举一反三有一个长方形，如果宽不变，长增加4米，面积就增加24平方米，如果长不变，宽增加3米，面积就增加36平方米，求原来长方形的面积。

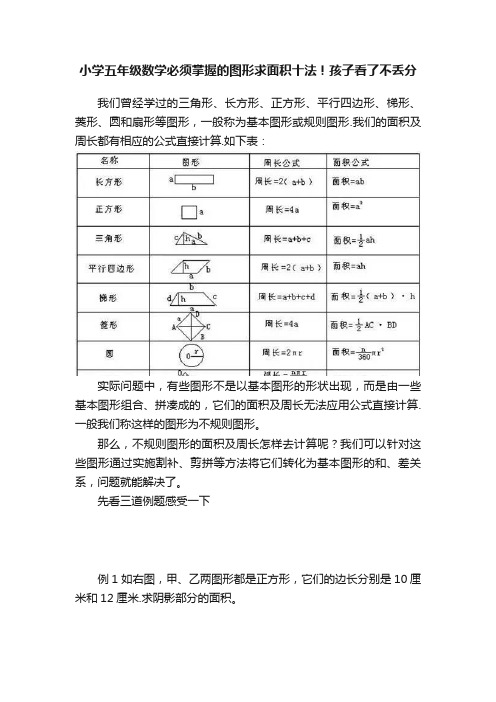
小学五年级数学必须掌握的图形求面积十法！孩子看了不丢分我们曾经学过的三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形，一般称为基本图形或规则图形.我们的面积及周长都有相应的公式直接计算.如下表：实际问题中，有些图形不是以基本图形的形状出现，而是由一些基本图形组合、拼凑成的，它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。

那么，不规则图形的面积及周长怎样去计算呢？我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系，问题就能解决了。

先看三道例题感受一下例1 如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米.求阴影部分的面积。

一句话：阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形（△ABG、△BDE、△EFG）的面积之和。

例2 如右图，正方形ABCD的边长为6厘米，△ABE、△ADF与四边形AECF的面积彼此相等，求三角形AEF的面积.一句话：因为△ABE、△ADF与四边形AECF的面积彼此相等，都等于正方形ABCD面积的三分之一，也就是12厘米.解：S△ABE=S△ADF=S四边形AECF=12在△ABE中，因为AB=6.所以BE=4，同理DF=4，因此CE=CF=2，∴△ECF的面积为2×2÷2=2。

所以S△AEF=S四边形AECF-S△ECF=12-2=10（平方厘米）。

例3 两块等腰直角三角形的三角板，直角边分别是10厘米和6厘米。

如右图那样重合.求重合部分（阴影部分）的面积。

一句话：阴影部分面积=S△ABG-S△BEF，S△ABG和S△BEF都是等腰三角形总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法一、相加法这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如：求下图整个图形的面积一句话：半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如：下图，求阴影部分的面积。

文章标题：深度探讨：五角星、正方形、三角形数学题的解析与思考一、引言在数学领域，五角星、正方形和三角形一直是研究的热点之一。

而有关这三种图形的数学题更是常常出现在学生的课本和数学竞赛中。

本文将针对这些数学题展开深度探讨，以便读者能更全面地理解这些图形之间的关系和性质。

二、五角星、正方形、三角形的基本性质1. 五角星五角星是一种几何图形，由五条等长的线段连接而成，其内部形成一个封闭的区域。

五角星是一个中心对称的图形，具有对称性和稳定性。

在数学题中，我们经常需要计算五角星的对角线长度、面积等相关问题。

2. 正方形正方形是一种特殊的四边形，具有四条相等的边和四个直角。

正方形是正规多边形中的一种，其特点是所有角均为直角。

在数学题中，我们通常需要求解正方形的对角线长度、周长和面积等问题。

3. 三角形三角形是一种具有三条边的几何图形，其内部形成一个封闭的区域。

根据角度的不同，三角形又可以分为直角三角形、等腰三角形、等边三角形等多种类型。

在数学题中，我们会涉及到三角形的边长、角度、高度以及面积等问题。

三、数学题的解析与思考1. 五角星、正方形和三角形的关系在解决数学题时，我们常常会遇到将五角星、正方形和三角形结合在一起的题目。

给定一个正方形，要求在其上绘制一个包含五角星和三角形的图案，并计算各个图形的面积和周长。

这就需要我们深入理解这些图形的性质和关联，灵活运用相关知识来解决问题。

2. 从简到繁，由浅入深地探讨为了更好地理解这些数学题，我们可以从简单的例子开始，逐步引入更复杂的情形。

可以先从计算各个图形的周长和面积开始，然后逐步引入相关的角度和对称性等概念，最终深入探讨这些图形的数学性质和应用。

3. 个人观点与理解在我看来，五角星、正方形和三角形是数学世界中的经典图形，它们不仅具有艺术美感，更重要的是具有丰富的数学性质和广泛的应用价值。

通过学习和探索这些图形之间的关系，我们可以锻炼自己的逻辑思维和数学推理能力，为今后的学习和工作打下坚实的基础。

元旦节的数学问题解析在欢度元旦的同时，我们也可以将数学知识应用到这个特殊的节日中。

本文将通过解析几个与元旦节相关的数学问题，让我们一起来探索数学与节日的奇妙结合。

问题一：元旦倒计时元旦节前夜，时钟指针指向凌晨12点，我们开始倒计时迎接新的一年。

假设此时时针、分针和秒针重合，问再过多久时分针会与秒针再次重合？解析：时针每小时走过30度，分针每小时走过360度，秒针每小时走过3600度。

当三者重合时，时针走过的角度记为θ，满足以下条件：θ = 30t，θ = 360t/60，θ = 3600t/3600。

将三个方程进行整合求解，可得t = 12小时。

因此，再过12小时时，时分针会再次重合。

问题二：元旦礼花元旦晚会上，璀璨的烟花绽放在夜空中，其中最受欢迎的烟花形状是圆形和五角星。

如果烟花半径为r，圆形烟花的面积为多少？五角星烟花的面积又是多少？假设五角星的五条边长度为a。

解析：圆形烟花的面积可以根据公式A = πr²求得，其中π取近似值3.14。

因此，圆形烟花的面积为A = 3.14r²。

五角星的面积可以分为五个三角形和一个中间的五边形。

每个三角形的面积可以通过海伦公式计算得出，其中a为五角星的五条边长度。

假设五角星的边长a = 2时，那么每个三角形的面积为A = √15。

因此，五角星的面积为A = 5 * (√15)/4。

问题三：元旦活动队伍一所学校举办元旦庆祝活动，共有A、B、C、D、E五个队伍参加。

这些队伍需要站成一列，其中A队伍在最左边，E队伍在最右边。

如果认为不同队伍之间的位置是可以交换的，请问一共有多少种不同的队伍排列方式？解析：根据排列组合的知识，我们可以知道共有5个队伍，所以一共有5！(5的阶乘)种排列方式，即5 * 4 * 3 * 2 * 1 = 120种。

因此，一共有120种不同的队伍排列方式。

问题四：元旦晚会门票一场元旦晚会门票分为A、B、C、D、E五个档次，对应的票价分别是200元、150元、100元、80元和50元。

五角星数学几何题
【实用版】
目录
1.五角星的数学与几何特征
2.五角星的构造方法
3.五角星在数学与几何中的应用
正文
五角星是一个具有五个顶点和五条边的几何图形，它也是一种特殊的星形。

在数学和几何学中，五角星有很多有趣的性质和应用，下面我们来详细探讨一下。

五角星的数学与几何特征：五角星可以被视为一个正五边形的一种延伸，它的每个内角为 108 度，而外角为 72 度。

五角星具有旋转对称性，可以被旋转 72 度后与自身重合。

同时，五角星也是黄金分割点的一个重要应用，它的每个顶点都是黄金分割点，可以将五角星分割成五个黄金分割点。

五角星的构造方法：五角星可以通过以下步骤来构造：首先，画一个正五边形，然后，在每个顶点处作一条射线，这些射线应该相交于一个点，这个点就是五角星的一个顶点。

接着，通过这个顶点，作一条射线连接正五边形的每一个顶点，这样就得到了五角星的另外四个顶点。

五角星在数学与几何中的应用：五角星在数学和几何中有广泛的应用，比如，在计算机图形学中，五角星经常被用来作为基本图形进行绘制。

此外，五角星也是许多科学和工程问题的解决方案的一部分，例如，五角星可以用来解决一些复杂的组合优化问题。

第1页共1页。

小学五边形面积公式大全
五边形是一个有五条边的多边形。

在小学数学中，我们主要研究以下几种五边形：
2.等腰五边形：五个顶点到中心点的距离都相等的五边形。

3.正五边形：既是等边五边形又是等腰五边形的五边形。

不规则五边形是指边长和内角大小都不相等的五边形。

不同的不规则五边形需要使用不同的公式来计算面积。

以下是常见的不规则五边形面积公式：
若已知某个底边和它对应的高，则可以使用基本公式：面积 = 底边长度 ×对应高
若已知五边形的外接圆半径，则可以使用公式：面积 = 2.5 ×外接圆半径² ×正弦36度
若已知五边形的五个顶点坐标(x1.y1)。

(x2.y2)。

(x3.y3)。

(x4.y4)。

(x5.y5)，可以使用海伦公式计算面积。

等边五边形的边长相等，因此可以使用以下公式计算面积：
正五边形既是等边五边形又是等腰五边形，因此可以使用以下公式计算面积：
根据五边形的不同类型，我们可以选择不同的面积公式来计算五边形的面积。

对于不规则五边形，可以根据边长、高度或顶点坐标来进行计算。

对于等边五边形
和正五边形，有特定的公式可以直接使用。

正确的使用面积公式可以帮助我们准确地计算五边形的面积。

根据五边形的不同类型，我们可以选择不同的面积公式来计算五边形的面积。

对于不规则五边形，可以根据边长、高度或顶点坐标来进行计算。

对于等边五边形和正五边形，有特定的公式可以直接使用。

正确的使用面积公式可以帮助我们准确地计算五边形的面积。

五角星的数学知识点一、五角星与三角形。

1. 内角和。

- 在五角星中，我们可以通过三角形的内角和知识来求解五角星的内角和。

五角星是由一个正五边形的五条对角线组成的图形。

- 把五角星的五个角分别看作是五个三角形的外角。

对于任意一个三角形，其内角和为180°。

- 以其中一个角为例，设这个角为∠A，它所在的三角形的另外两个内角之和等于与∠A相邻的那个三角形的一个内角（因为这两个角是对顶角相等）。

- 我们知道多边形的外角和是360°，五角星的五个角是五个三角形的外角，所以五角星的内角和为180°×5 - 360°=180°。

2. 等腰三角形相关。

- 在标准的正五角星中，存在许多等腰三角形。

例如，连接五角星相邻的两个顶点以及五角星中心所构成的三角形是等腰三角形。

- 设正五角星的边长为a，我们可以利用等腰三角形的性质，如两腰相等，底角相等来进行一些计算。

如果我们知道等腰三角形的顶角（例如在正五角星中这个顶角是36°），根据三角形内角和定理，就可以求出底角为(180° - 36°)÷2 = 72°。

二、五角星与黄金分割。

1. 线段比例关系。

- 正五角星中存在着黄金分割比例关系。

如果把正五角星的一条边看作单位长度1。

- 从五角星的一个顶点到与其不相邻的顶点的线段长度与五角星边长之比是黄金分割比，约为1.618。

- 例如，设正五角星的边长AB = 1，连接AC（C为与A不相邻的顶点），则AC:AB≈1.618。

这种黄金分割关系在五角星的美学设计等方面有着重要的应用。

三、五角星与正多边形。

1. 与正五边形的关系。

- 正五角星与正五边形密切相关。

正五边形的五条对角线构成了正五角星。

- 正五边形的内角和为(5 - 2)×180° = 540°，每个内角为540°÷5 = 108°。

数学：五角星与六边形的计算和性质知识点：五角星与六边形的计算和性质一、五角星的计算和性质1.五角星的定义：五角星是一种由五条线段连接五个顶点的几何图形。

2.五角星的计算：(1)五角星的周长：五角星的周长等于其五条边的长度之和。

(2)五角星的面积：五角星的面积可以通过分割成小三角形的方法进行计算。

3.五角星的性质：(1)五角星的所有顶点、边和角都相等。

(2)五角星的每个内角为108度。

(3)五角星的对角线互相垂直且平分。

二、六边形的计算和性质1.六边形的定义：六边形是一种由六条线段连接六个顶点的几何图形。

2.六边形的计算：(1)六边形的周长：六边形的周长等于其六条边的长度之和。

(2)六边形的面积：六边形的面积可以通过分割成小三角形的方法进行计算。

3.六边形的性质：(1)六边形的所有顶点、边和角都相等。

(2)六边形的每个内角为120度。

(3)六边形的对角线互相垂直且平分。

三、五角星和六边形的联系与区别1.联系：五角星和六边形都是多边形，它们的边数相同，都是五条。

2.区别：五角星是由五个顶点组成的，而六边形是由六个顶点组成的。

五角星的每个内角为108度，六边形的每个内角为120度。

四、五角星和六边形的实际应用1.五角星的应用：五角星常用于表示荣誉、重要事件或军事标志等。

2.六边形 applications: Hexagons are commonly found in nature, such asin the structure of honeycombs and the arrangement of leaves on some plants.They also have applications in various fields, including engineering,architecture, and computer science.五角星和六边形是两种特殊的多边形，它们具有一定的计算和性质。