巧求面积(上)

巧算面积的七种方法
《巧算面积的七种方法》
１、古典梯形法
众所周知，梯形是以一条垂线为分界，两个直角边在一边，二个钝角边在另一边的四边形，面积的计算方法是将梯形分成两个三角形，用三角形的公式即可，即A = 1/2 (a + b) * h，其中a、b分别为梯形的底边长度，h为梯形的高。

2、测量法
测量法是最简单有效的面积计算方法，只要将物体边缘分别测量出来，然后将测量出来的尺寸记录下来，最后求和就可以得出物体的面积。

3、尺规法
尺规法也是一种常用的面积计算方法，其具体操作为：使用尺规将物体边界轮廓放大或缩小到尺规上，根据尺规刻度记录出轮廓的长度就可以计算出面积了。

4、数学方法
如果地面的图形符合一定的数学方程，例如椭圆、抛物线等，那么可以通过数学方法，借助积分的方式计算出面积。

例如，用积分计算椭圆面积的公式为A = 3/2 * pi * a * b，其中a、b分别为椭圆的短半轴和长半轴长度。

5、立体几何法
立体几何法是一种非常神奇、有效的面积计算方法。

它依据立体几何的几何关系建立模型，根据立体几何的有关定律解出问题的求解方法，这种方法十分的有效。

6、计算机技术法
随着科技的发展，计算机技术也发展得很快，许多计算机软件已经可以非常方便地计算出地面物体的面积了，主要是根据空间几何关系来计算，所以很精确，而且快速。

7、三点定标法
三点定标法是一种利用GPS技术测量工程地物面积的方法，其原理是将地物内部三点定向，并记下该三点之间的距离，最后将距离相乘即可得出地物的面积。

总结
以上就是常用的七种面积计算方法，不仅效率高，而且精确度也非常高，它们可以满足各种不同的地物测量需求，获得更准确更有效的结果。

第一讲：巧求面积一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了（如图）。

二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可（如图）。

例.一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米．求原正方形的面积？三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它是一个底2，高4的三角形，就可以直接求面积了（如图）。

例.如下图，长方形AFEB和长方形FDCE拼成了长方形ABCD ，长方形 ABCD的长是20，宽是12，则它内部阴影部分的面积是．四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了（如图）。

例.已知大正方形边长是7厘米，小正方形边长5厘米，求阴影部分的面积。

五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如图）。

六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半（如图）.例.求阴影部分的面积。

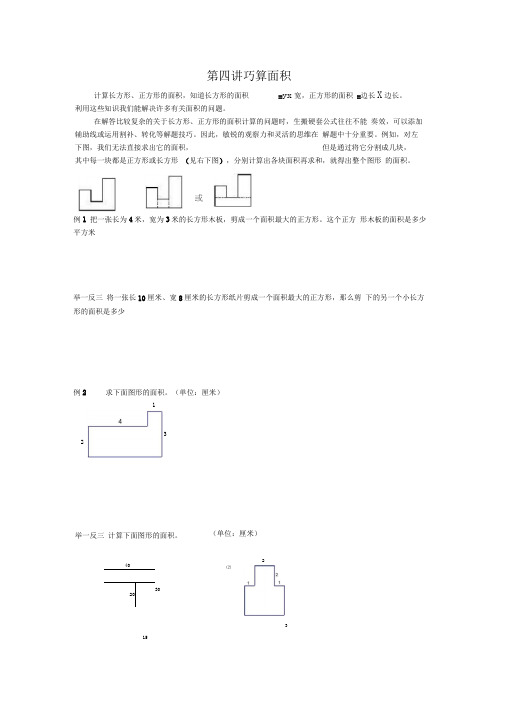
第四讲巧算面积计算长方形、正方形的面积，知道长方形的面积=yx宽，正方形的面积=边长X边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例如，对左下图，我们无法直接求出它的面积，但是通过将它分割成几块，其中每一块都是正方形或长方形（见右下图），分别计算出各块面积再求和，就得出整个图形的面积。

或例1 把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米举一反三将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形，那么剪下的另一个小长方形的面积是多少例2 求下面图形的面积。

（单位：厘米）132举一反三计算下面图形的面积。

（单位：厘米）2⑵3020315例3 有两个相同的长方形，长是8厘米，宽是3厘米。

如果把它们按下图叠放，这个图形的面积是多少举一反三求下图中阴影部分的面积。

（单位：分米）7例4 一个长方形若长增加2厘米，面积就增加10平方厘米，若宽减少3厘米，面积就减少18平方厘米。

求原来长方形的面积。

举一反三一个长方形，若长减少5厘米，面积就减少50平方厘米，若宽增加7厘米，面积就增加28平方厘米。

原来长方形的面积是多少平方厘米例5 右图为一个长50米、宽25米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖（阴影部分）。

求游泳池面积和地砖面积。

举一反三有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少例6 一个边长为10米的正方形花坛，依次连接四边中点得到一个小正方形的喷泉，求小正方形喷泉的面积。

<1例7 一个长方形，如果宽增加2厘米，或长增加3厘米，他们的面积都增加120平方厘米，原来长方形的面积是多少举一反三 有一个长方形，如果宽不变，长增加 4米，面积就增加24平方米, 如果长不变，宽增加3米，面积就增加36平方米，求原来长方形的面积。

第一讲巧求面积本讲巩固1.右图中有一个边长为6厘米的正方形ABCD与一个斜边长为8厘米的等腰直角三角形AEF，E在AB的延长线上，则图中阴影部分的面积为________平方厘米.2如图，正方形ABCD与正方形EFGH的边长分别为8和5，若C与G重合，F在BC的延长线上，H在DC的延长线上，则三角形BDE的面积是________平方厘米.3.如图所示,正方形ABCD的边长是18,E是CD中点,且ABFH是长方形,两个阴影三角形面积相等.那么,四边形AEFB的面积是________.4.如图,将原三角形向上平移2厘米,再向左平移3厘米后,求新三角形与原三角形不重叠部分(即阴影部分)的面积为_________平方厘米.5.图中长方形ABCD的长为6m宽为4m,已知阴影①比阴影②的面积少3 cm²,则EC的长为_____( )A. 9cmB. 5cm C .4cm6.如图所示,正方形ABCD的边长为12,直角梯形CEFG的上底、下底和高分别为4、14和15,已知AH=9,则阴影部分的面积为_________.7.如图中的长方形被分割成6个正方形,已知中央小正方形的面积是16平方厘米,则原来长方形的面积为________平方厘米.基础过关1.手工课上,刘老师给大家发了一大一小两个正方形,琪琪、思思和妙妙分别把这两个正方形摆成了如下图所示的样子,同时给一些地方涂上了颜色,请你分别求图中阴影部分的面积.(1) (2) (3)2.右图中的三角形都是等腰直角三角形.图中阴影部分的面积( ).A.4.25B.4.5C.8.5D.10.53.如图正方形ABCD边长是12cm,长方形EFGH的长为10cm,宽为6cm,阴影部分甲与阴影部分乙的面积差是___________平方厘米.4.如图,AD=2,AC=4,CE=6,已知阴影甲-阴影乙=4,则BD=_________.能力提升1.如图,3个边长分别为3、4、12的小正方形各覆盖了边长为13的大正方形的一部分,那么边长为13的大正方形中阴影部分的面积与3个小正方形中阴影部分面积的差是_________.2.如图,图中正方形的面积依次为4、16、36、64、100,则阴影部分的面积为_________.3.如图,一个3×3正方形网格,如果小正方形的边长是1,那么阴影部分的面积是( ).A.5B.4C.3D.24.已知五边形的三条边的长和四个角的大小,如下图所示,那么这个五边形的面积是______平方厘米.创新挑战1.如图,D是三角形ABC一边上的中点,两个长方形分别以B、D为顶点,并且有一个公共顶点E,已知两块阴影部分的面积分别是100和120,则三角形BDE的面积是_______.2.如图,等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上,连接AE、AD、AF,于是整个图形被分成五块小三角形,图中已标出其中三块的面积,那么△ABC的面积是_________.。

第十六讲巧求面积学习目标1、在长方形和正方形面积公式的基础上，学习割补法、添补法和分割法求图形面积。

2、尝试求不规则图形的面积，提高空间想象能力，能根据题目合理选择解题方法。

一、知识回顾1、教室南面的墙壁长9米，宽3米，墙上有2扇窗户，每扇窗户的面积是2平方米。

现在要粉刷这面墙，要粉刷的面积是多少平方米?二、例题辨析例1、求下面图形的面积。

小结:变式练习1:求下列图形的面积。

（单位:厘米）例2、有两个完全相同的长方形，长8厘米，宽2厘米，如果把它们按下图叠放，这个图形的面积是多少?小结:变式练习2:（1）你能求出下图中阴影部分的面积吗? 1分米1分米6分米10分米（2）如图长方形的面积是（）平方厘米。

1平方米例3、一张桌子长100厘米、宽80厘米，要在这张桌子上铺一块台布，要使台布在桌子的四周都垂下20厘米，应买一块多少平方分米的台布?变式练习3:一个长方形花坛，长25米，宽15米，要在这个长方形花坛四周铺上宽为20分米的鹅卵石路，问花坛和小路的占地面积各是多少?三、归纳总结1、分割法:把组合图形转化成几个基本图形，然后分别求出几个基本图形的面积，再把各基本图形的面积相加。

2、添补法:把原图形添补成一个大图形，大图形中包含小图形，计算时先算出每个图形的面积，然后从大图形的面积中减去小图形的面积，就是原图形的面积。

3、割补法:指把一个图形的某一部分割下来，填补在图形的另一部分，在面积不变的情况下使其转化为已经掌握的图形，使题目便于解答。

四、拓展延伸例:为美化环境，九洲校区新建了两块草坪，并在草坪重合处修建了一个正方形花坛。

草坪的面积是多少?长方形剩余草坪面积与正方形剩余草坪面积相差多少?小结:变式练习:一个长方形和一个正方形部分重合（如下图），求没有重合的空白部分的面积相差多少?（单位:厘米）五、课后作业1、求下面图形的面积。

（单位:米）2、小青家要重新粉刷客厅电视墙面的墙壁。

已知墙壁长6米，高3米，墙上放电视的部分是一个边长2米的正方形（不需要粉刷，直接张贴壁纸）。

2011秋季学而思奥数测试题答案第1题 (本题10分)（★★）有一列数：l，2，4，7，1l，16，22，29，37，问这列数第15个数是多少?1.A 1052.B 1063.C 1104.D 104正确率：有69%的网校学员答对了该题知识点：数列正确答案：B试题讲解：第2题 (本题10分)1.A 6012.B 600C 5993.4.D 602正确率：有50%的网校学员答对了该题知识点：数列计算正确答案：A试题讲解：第3题 (本题10分)1.A 1252.B 1303.C 1004.D 98正确率：有85%的网校学员答对了该题知识点：数列计算正确答案：C试题讲解：第4题 (本题10分)1.A 452.B 603.C 284.D 50正确率：有73%的网校学员答对了该题知识点：数列计算正确答案：D试题讲解：第5题 (本题10分)（★★★）在1~300这三百个自然数中，所有能被4整除的数的和是多少？1.A 114002.B 114403.C 112404.D 12400正确率：有70%的网校学员答对了该题知识点：数列求和正确答案：A试题讲解：第6题 (本题10分)（★★★★）56个互不相同的非零自然数之和为2800，问最少有多少个偶数？1.A 32.B 53.C 44.D 6正确率：有65%的网校学员答对了该题知识点：数列正确答案：C试题讲解：===================================================================== 第1题 (本题10分)A 49501.2.B 50503.C 5051D 60504.正确率：有100%的网校学员答对了该题知识点：数列求和正确答案：B试题讲解：第2题 (本题10分)A 20130211.2.B 20140243.C 20150284.D 2016033正确率：有100%的网校学员答对了该题知识点：数列求和正确答案：C试题讲解：第3题 (本题10分)1.A 50472.B 5050C 101003.4.D 10094正确率：有100%的网校学员答对了该题知识点：数列求和正确答案：A试题讲解：第4题 (本题10分)1.A 48932.B 49003.C 48914.D 4901正确率：有100%的网校学员答对了该题知识点：平方差公式正确答案：C试题讲解：第5题 (本题10分)1.A 125262.B 125273.C 125284.D 12529正确率：有80%的网校学员答对了该题知识点：平方和公式正确答案：D试题讲解：第6题 (本题10分)1.A 3382802.B 3383203.C 3383504.D 338380正确率：有60%的网校学员答对了该题知识点：平方和公式正确答案：B试题讲解：第1题 (本题10分)桌子上放着40根火柴，甲、乙二人轮流每次取走根。

第五讲巧求面积例1：某工人要裁切一块长方形铁皮。

如果宽截去3米，或者长截去5米，则面积均减少了30平方米。

那么这块铁皮原来的面积是多少？练习1：有一个长方形，如果宽减少2米或长减少3米，则面积均减少24平方米。

求这个长方形原来的面积。

判断：请在正确的说法后面打“√”，在错误的说法后面打“×”（1）下图中两个长方形菜地面积相等。

如果灰色的小路面积也相等，那么白色的区域面积相等。

（）（2）下图中两个长方形菜地面积相等。

如果灰色的小路面积也相等，那么白色的区域面积相等。

（）（3）下图中两个长方形菜地面积相等。

如果灰色的小路面积也相等，那么白色的区域面积相等。

（）例2：如图，一块正方形桌布边长18厘米，桌布的白底上横竖各有两道宽2厘米的色条。

这块桌布白色部分的面积是多少？练习1：如图，一块白底的正方形桌布边长16厘米，桌布的中间横竖有两道宽为3厘米的色条。

这块桌布白色部分的面积是多少?判断：如图，已知长方形ABCD的面积是18平方米，长方形ECGF的面积是20平方米，长方形ECDH的面积是4平方米，请根据条件在正确的结论后面打“√”，在错误的结论后面打“×”。

（1）右图的面积：20+18=38（平方米）（2）右图的面积：20+18+4=42（平方米）（3）右图的面积：20+18-4=34（平方米）我发现：例3：如图，一块正方形的玻璃，长截去2厘米，宽截去3厘米后，剩下的小长方形比原来少29平方厘米。

这块正方形玻璃原来的面积是多大？练习1：一块正方形的玻璃，长截去2厘米，宽截去6厘米后，剩下的小长方形比原来少308平方厘米。

原来正方形玻璃的面积是多少平方厘米？课后作业：1、一个长方形的长增加3米，长方形的面积就增加12平方米;如果宽减少2米，长方形面积就减少14平方米。

原来的长方形面积是多少平方米?2、如图，一块白底的正方形桌布边长60厘米，桌布的中间横竖有3道宽为2厘米的色条。

这块桌布白色部分的面积是多少?3、一块正方形的玻璃，一边截去4厘米，另一边截去3厘米后，剩下的小长方形比原正方形少44平方厘米。