巧求面积

巧算面积的七种方法
《巧算面积的七种方法》
１、古典梯形法
众所周知，梯形是以一条垂线为分界，两个直角边在一边，二个钝角边在另一边的四边形，面积的计算方法是将梯形分成两个三角形，用三角形的公式即可，即A = 1/2 (a + b) * h，其中a、b分别为梯形的底边长度，h为梯形的高。

2、测量法
测量法是最简单有效的面积计算方法，只要将物体边缘分别测量出来，然后将测量出来的尺寸记录下来，最后求和就可以得出物体的面积。

3、尺规法
尺规法也是一种常用的面积计算方法，其具体操作为：使用尺规将物体边界轮廓放大或缩小到尺规上，根据尺规刻度记录出轮廓的长度就可以计算出面积了。

4、数学方法
如果地面的图形符合一定的数学方程，例如椭圆、抛物线等，那么可以通过数学方法，借助积分的方式计算出面积。

例如，用积分计算椭圆面积的公式为A = 3/2 * pi * a * b，其中a、b分别为椭圆的短半轴和长半轴长度。

5、立体几何法
立体几何法是一种非常神奇、有效的面积计算方法。

它依据立体几何的几何关系建立模型，根据立体几何的有关定律解出问题的求解方法，这种方法十分的有效。

6、计算机技术法
随着科技的发展，计算机技术也发展得很快，许多计算机软件已经可以非常方便地计算出地面物体的面积了，主要是根据空间几何关系来计算，所以很精确，而且快速。

7、三点定标法
三点定标法是一种利用GPS技术测量工程地物面积的方法，其原理是将地物内部三点定向，并记下该三点之间的距离，最后将距离相乘即可得出地物的面积。

总结
以上就是常用的七种面积计算方法，不仅效率高，而且精确度也非常高，它们可以满足各种不同的地物测量需求，获得更准确更有效的结果。

第一讲：巧求面积一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，右图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了（如图）。

二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，右图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可（如图）。

例.一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米．求原正方形的面积？三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它是一个底2，高4的三角形，就可以直接求面积了（如图）。

例.如下图，长方形AFEB和长方形FDCE拼成了长方形ABCD ，长方形 ABCD的长是20，宽是12，则它内部阴影部分的面积是．四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求右图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了（如图）。

例.已知大正方形边长是7厘米，小正方形边长5厘米，求阴影部分的面积。

五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如右图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便（如图）。

六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如右图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半（如图）.例.求阴影部分的面积。

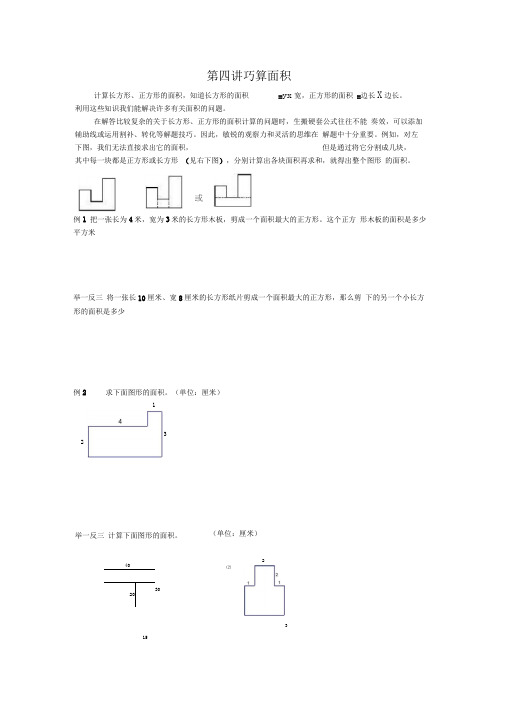
第四讲巧算面积计算长方形、正方形的面积，知道长方形的面积=yx宽，正方形的面积=边长X边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例如，对左下图，我们无法直接求出它的面积，但是通过将它分割成几块，其中每一块都是正方形或长方形（见右下图），分别计算出各块面积再求和，就得出整个图形的面积。

或例1 把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米举一反三将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形，那么剪下的另一个小长方形的面积是多少例2 求下面图形的面积。

（单位：厘米）132举一反三计算下面图形的面积。

（单位：厘米）2⑵3020315例3 有两个相同的长方形，长是8厘米，宽是3厘米。

如果把它们按下图叠放，这个图形的面积是多少举一反三求下图中阴影部分的面积。

（单位：分米）7例4 一个长方形若长增加2厘米，面积就增加10平方厘米，若宽减少3厘米，面积就减少18平方厘米。

求原来长方形的面积。

举一反三一个长方形，若长减少5厘米，面积就减少50平方厘米，若宽增加7厘米，面积就增加28平方厘米。

原来长方形的面积是多少平方厘米例5 右图为一个长50米、宽25米的标准游泳池。

它的四周铺设了宽2米的白瓷地砖（阴影部分）。

求游泳池面积和地砖面积。

举一反三有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少例6 一个边长为10米的正方形花坛，依次连接四边中点得到一个小正方形的喷泉，求小正方形喷泉的面积。

<1例7 一个长方形，如果宽增加2厘米，或长增加3厘米，他们的面积都增加120平方厘米，原来长方形的面积是多少举一反三 有一个长方形，如果宽不变，长增加 4米，面积就增加24平方米, 如果长不变，宽增加3米，面积就增加36平方米，求原来长方形的面积。

第二讲 巧求面积一、常用面积公式二、剪拼及构造思想很多题往往不能直接用公式算出来，这时应灵活思考，把原图尽量剪拼或构造成比较容易算的图形。

（该能力的培养及熟练掌握需要同学们大量练题） 1、割补：把不规则的剪拼为规则的、好算的。

2、容斥（重叠原理）：若在计算中出现重叠的情况，把多算的减出去即可。

例1 如图，一张长方形纸片，长7厘米，宽5厘米， 把它的右上角往下折叠，再把左下角往上折叠，未盖 住的阴影部分的面积是多少平方厘米？解析：本题的隐藏条件，右边及左下方均为正方形。

法一：阴影部分为长方形，尝试找它的长与宽长：7-5=2（CM） 宽：5-2=3（CM） 面积：3×2=6（CM 2）法二：阴影部分包含于大长方形中，可用大长方形的面积-两个正方形的面积大长方形面积：7×5=35（CM 2）两正方形面积：5×5+（7-5）×（7-5）=29（CM 2）阴影面积：35-29=6（CM 2）例2 一块长方形草坪（图中阴影部分）长是宽的2倍， 它的四周围是总面积为34平方米的1米宽的小路，求 草坪的面积是多少平方米？解析：面积已知的小路形状并不规则，我们可以先把它切割为规则的图形，如右图4个角都是边长为1米的正方形，其余是4个宽为1的长方形。

且A=2B34-4=30（M 2） ……减去4个角的面积30÷3=10（M 2）……2个B 合起来是1个A 的面积，一共就是3个A 的面积，所以÷3 草坪的长10÷1=10（M） 宽:10÷2=5（M）面积：10×5=50（M 2）S=abAA B B例3 一块长方形铁板，长15分米，宽12分米，如果长和宽各减少2分米，面积比原来减少多少平方分米？（图略）法一：将减少的部分切割为两个规则的长方形，求其面积和。

算式略法二：用大长方形面积减去小长方形面积就是所求面积大长方形：15×12=180（DM2）小长方形：（15-2）×（12-2）=130（DM2）减少的面积：180-130=50（DM2）例4 如图所示，外侧大正方形的边长是10cm，在里面画两条对角线、一个圆、两个正方形，阴影总面积为26cm2，最小的正方形的边长为多少厘米？解析：观察本图是一对称图形，阴影部分的面积不易一一求得，那就利用剪拼，将它们拼补在一块。

方法技巧练——巧求面积相加法：将不规则图形分解,转化成几个基本规则图形,分别计算它们的面积,然后相加,求出整个图形的面积。

1.计算下面图形的面积。

(单位:厘米)相减法:将所求的不规则图形的面积看成是多个基本规则图形的面积之差。

2.计算下面图形的面积。

(单位:厘米)平移法:将图中某一部分平行移动到一个恰当的位置,使之组成一个新的基本规则图形。

3.如下图,正方形的边长是11米,中间长方形的宽为1米。

求图中阴影部分的面积。

4.有一块菜地,如下图,长43米,宽29米。

菜地中间留有宽1米的小路,把菜地平均分成四块,每块的面积是多少平方米?答案1.方法一:18×15=270(平方厘米) (40-15)×35=875(平方厘米)270+875=1145(平方厘米) 方法二:40×18=720(平方厘米)(40-15)×(35-18)=25×17=425(平方厘米) 720+425=1145(平方厘米)2.36×20=720(平方厘米) 18×4=72(平方厘米) 720-72=648(平方厘米)3.11×11=121(平方米) 11×1×2-1×1=22-1=21(平方米) 121-21=100(平方米)[提示:本题也可以将中间长方形平移到正方形的边上,用正方形面积减去空白长方形面积等于阴影部分面积,如右图。

] 4.43×29=1247(平方米) 43×1+29×1=72(平方米) 1247-72+1=1176(平方米) 1176÷4=294(平方米)。

1、一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米；如果长不变，宽减少3米，那么它的面积减少36平方米。

这个长方形原来的面积是多少平方米？
2、一块正方形的钢板，先截去宽5分米的长方形，又截去宽8分米的长方形（如图），面积比原来的正方形减少181平方分米。

原正方形的边长是多少？
3、如下图，六个相同的长方形围成了大小两个正方形，已知小正方形的面积是36平方厘米，则每个小长方形的面积是多少平方厘米？
4、把长方形的长去掉8厘米后，余下的是一个面积49平方厘米的的正方形，原来长方形的面积是多少？
5、一个长50米，宽25米的游泳池，四周铺2米宽的走道，走道的面积是多少平方米？
6、人民路小学操场长90米，宽45米，改造后，长增加10米，宽增加5米。

现在操场面积比原来增加多少平方米？
7、一个养禽专业户用一段长16米的篱笆围成一条边长是6厘米的长方形养鸡场，求占地面积有多大。

8、一块正方形的钢板，先截去宽5分米的长方形，又截去宽8分米的长方形（如下图），面积比原来的正方形减少181平方分米，原正方形的边长是多少？
9、一块正方形的玻璃，长和宽都截去8厘米后，剩下的正方形比原来少448平方厘米，这块正方形玻璃原来的面积是多大？。