轮胎纵向动力学
- 格式:pptx
- 大小:7.74 MB
- 文档页数:22







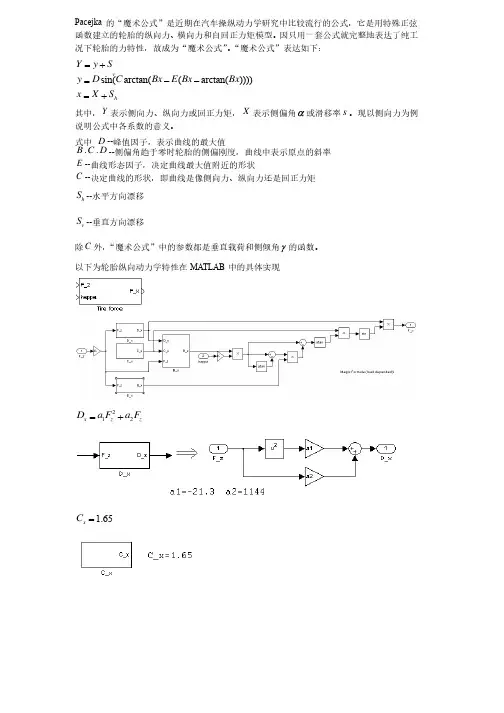
Pacejka 的“魔术公式”是近期在汽车操纵动力学研究中比较流行的公式,它是用特殊正弦函数建立的轮胎的纵向力、横向力和自回正力矩模型。
因只用一套公式就完整地表达了纯工况下轮胎的力特性,故成为“魔术公式”。
“魔术公式”表达如下:sin(arctan((arctan())))vhY y Sy D C Bx E Bx Bx x X S =+=--=+其中,Y 表示侧向力、纵向力或回正力矩,X 表示侧偏角a 或滑移率s 。
现以侧向力为例说明公式中各系数的意义。
式中D --峰值因子,表示曲线的最大值B C D ××--侧偏角趋于零时轮胎的侧偏刚度,曲线中表示原点的斜率E --曲线形态因子,决定曲线最大值附近的形状C --决定曲线的形状,即曲线是像侧向力、纵向力还是回正力矩h S --水平方向漂移v S --垂直方向漂移除C 外,“魔术公式”中的参数都是垂直载荷和侧倾角g 的函数。
以下为轮胎纵向动力学特性在MA TLAB中的具体实现212x z zD a F a F =+1.65x C=2678x zz E a F a F a =++5234()///za F x z z x x B a F a F e C D =+52342122678sin(arctan((arctan())))()///1.65zx x x x x x x a F x z z x xx xz zxzz F D C B E B B B a F a F e C D C D a F a F E a F a F a k k k =--=+==+=++sin(arctan((arctan())))(arctan((arctan())))cos(arctan((arctan())))x xx x x x x z zx x x x xxxxxxxzdF dD C B E B B dF dF d B E B B D C B E B B CdF k k k k k k k k k =--+----2(arctan((arctan())))(arctan())1((arctan()))1((arctan()))x x x x z x x x x x x xx x x x z z z d B E B B dF dB dE d B B B B E B E B B dFdF dF k k k k k k k k k k k --=----+--222(arctan())()11()1()xx xxxx zz x z x z d B B dB dB B dB dF dF B dF B dFk k k k k k k k -=-=++ 555522343422234345(()///)()///(()///)(()///)zzzza F a F xzzx x z z xxz zza F a F x z z x x z z x x zdBd a F a F eC D d a F a F eC D dF dF dF dD a F a F eC D a F a F eC D a dF ++==-+-+sin(arctan((arctan())))x x x x x x x F D C B E B B k k k =--22cos(arctan((arctan())))(())1()1((arctan())x xxxxxxxxxxxxx x x x B D C BE BB C B E B dF B d B E B B kkkk kk k k ----+=+--车辆防抱死制动系统的控制技术研究车辆防抱死制动系统的控制技术研究 东大,侯光钰,张为公东大,侯光钰,张为公2.3.1 H.B.Pacejka 的魔术公式的魔术公式Pacejka 的“魔术公式”是汽车操纵动力学研究中应用比较广泛的轮胎力学模型,它用特殊的正弦函数建立轮胎的纵向力、横向力和回正力矩的函数表达式。



dugoff轮胎模型公式
Dugoff轮胎模型是汽车控制领域中最为常用的轮胎模型之一,其被广泛应用于车辆动力学、底盘控制和智能驾驶等领域。
该模型基于轮胎与地面之间的相互作用力,通过一组方程来描述轮胎在转动过程中产生的摩擦力、滑移率和侧偏角等关键参数。
下面是Dugoff轮胎模型的具体方程:
1. 横向力(Fy)公式
Fy = D*sin[C*arctan{B*(1-E)*α+B*E*arctan(C*α)}]
其中,D表示滑移率变化幅度的最大值,B是形状参数,C是侧偏角曲线的形状参数,E是轮胎面形因素,α是侧偏角。
2. 纵向力(Fx)公式
Fx = D*sin[C*arctan{B*(1-E)*α+B*E*arctan(C*α)}]*cos(γ)
其中,γ表示轮胎与地面间的夹角。
3. 滑移率(κ)公式
κ = (v - rω)/v
其中,v是轮胎的速度,r是轮胎半径,ω是轮胎的角速度。
4. 侧偏角(α)公式
tan(α) = (y + rγ)/x
其中,x、y分别为轮胎与地面间接触点的坐标,γ表示轮胎与地面间的夹角。
通过以上方程,可以计算得到轮胎在旋转时产生的摩擦力、滑移率和侧偏角等重要参数,从而更加准确地模拟车辆的运动状态。
这对于提高汽车控制系统的性能和安全性具有重要意义。
轮胎纵向力-滑动率关系曲线
在这条曲线上,横轴表示轮胎的滑动率,即轮胎滑动速度与车辆速度之比,通常用百分比表示;纵轴表示轮胎所产生的纵向力,即轮胎与地面之间的摩擦力。
通过这条曲线,我们可以了解到在不同的滑动率下,轮胎所能提供的最大纵向力,以及在不同道路条件下的汽车性能表现。
曲线的形状通常呈现出一个峰值,即在某一滑动率下轮胎能够提供最大的纵向力。
这个峰值对应着最佳的车辆加速、制动和操控性能。
在这个点上,轮胎能够提供最大的附着力,使得车辆能够更好地应对各种路况和驾驶操作。
了解轮胎纵向力-滑动率关系曲线对于汽车制造商和工程师来说至关重要。
他们可以通过对这条曲线的研究和分析,来设计出更优秀的轮胎和车辆悬挂系统,从而提高汽车的性能和安全性。
此外,对于驾驶员来说,了解这条曲线也可以帮助他们更好地理解车辆的性能特点,从而更加安全地驾驶汽车。
在不同的路况和驾驶操作下,驾驶员可以根据轮胎纵向力-滑动率关系曲线来调整驾驶策略,以获得更好的操控性能和安全性。
总之,轮胎纵向力-滑动率关系曲线是汽车工程中非常重要的一
部分,它对于汽车的性能和安全性有着重要的影响。
通过对这条曲
线的研究和分析,可以帮助汽车制造商设计出更加优秀的汽车产品,同时也可以帮助驾驶员更加安全地驾驶汽车。
汽车轮胎动力学及性能评价研究随着汽车工业的发展,车辆的性能和安全性成为汽车制造商和消费者关注的重要方面。
而轮胎作为车辆与地面之间的唯一接触点,其动力学和性能评价研究变得至关重要。
在本篇文章中,将重点探讨汽车轮胎动力学及性能评价的研究现状和方法。
首先,我们将从动力学的角度来介绍汽车轮胎的研究。
汽车轮胎的动力学研究主要包括力学特性、刚度、变形和摩擦等方面。
轮胎的力学特性主要包括侧向、纵向和径向刚度。
侧向刚度反映了轮胎在转弯时的抓地能力,而纵向刚度则与轮胎的加速和制动能力有关。
径向刚度则决定了轮胎在行驶过程中的承载能力和稳定性。
另外,轮胎的变形也是一个重要的动力学特性。
轮胎在汽车行驶过程中会出现一定的变形,如压缩、伸展和弯曲等。
这些变形对轮胎的性能和安全性有着重要影响。
摩擦则是轮胎与地面之间传递力的关键因素。
轮胎的摩擦特性影响了汽车的抓地能力、操控性和燃油效率等。
除了动力学特性外,轮胎的性能评价研究也是非常重要的。
轮胎的性能评价主要涉及到耐磨性、抗剪切性、抗破裂性、抗老化性和抗腐蚀性等方面。
耐磨性是指轮胎在长期行驶中所能承受的摩擦磨损。
轮胎的抗剪切性则决定了其能否承受转向和加速等动力学力的作用。
抗破裂性和抗老化性则关系到轮胎的使用寿命和安全性。
另外,轮胎还需要具备抗腐蚀性以应对恶劣的环境条件。
为了研究汽车轮胎的动力学和性能评价,学者们采用了多种方法。
实验方法是其中最常见的研究方式之一。
通过在实验室中创建各种条件下的试验环境,研究人员可以准确地测量和分析轮胎的力学特性和性能。
此外,建立数学模型也是常用的研究方法之一。
通过数学模型的构建,研究人员可以模拟轮胎在不同条件下的力学特性和性能。
计算机模拟则是数学模型的延伸,通过建立计算机模型可以更加准确地模拟和分析轮胎的动力学和性能评价。
尽管汽车轮胎动力学及性能评价的研究已经取得了一定的进展,但仍然存在一些挑战和问题需要解决。
首先,轮胎的动力学和性能评价受到多种因素的影响,如温度、载荷、速度和路面条件等。