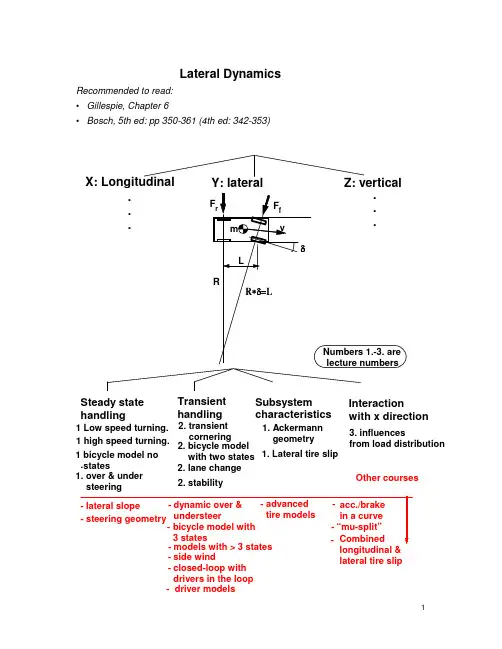
Lateral DynamicsRecommended to read:• Gillespie, Chapter 6• Bosch, 5th ed: pp 350-361 (4th ed: 342-353)Z: verticalInteractionwith x directionOther coursesX: Longitudinal Y: lateralSubsystem characteristicsSteady state handlingTransient handling1. over & under steering2. stability2. lane change1. Lateral tire slip 1 bicycle model no stateslateral tire slip2. bicycle modelwith two states 1. Ackermanngeometry- side wind2. transient cornering 1 Low speed turning. 1 high speed turning. - driver models- closed-loop with drivers in the loop3. influences from load distribution.General questionsSketch your view of the open- and closed-loop system, i.e. without and with the driver. Use a control system block diagram or similarOpen-loop vs closed loop studies of lateral dynamics. Closed-loop studies involve the driver response to feedback in the system. See text in Gillespie, p195, Bosch 5th ed p 354 (4th ed p 346).This course will only treat open-loop vehicle dynamics. How can we upgrade to closed-loop? For example: driver models, simulators or experimentsQuestions on low speed turningDraw a top view of a 4 wheeled vehicle during a turning manoeuvre. How should the wheel steering angles be related to each other for perfect rolling at low speeds?Ackermann steering geometry Array Deviations from Ackerman geometry affect tire wear and steering system forcessignificantly but less influence on directional response.Consider a rigid truck with 1 steered front axle and 2 non-steered rear axles. How do we predict the turning centre?Assume: low speed, small steering angles, low traction.We still cannot assume that each wheel is moving as it is directed. A lateral slip iscreated at all axles. The turning centre is then not only dependent of geometry, but also forces. The difference in the 3 axle vehicle compared to the two axle vehicle is that we now have 3 unknown forces but only 2 relevant equilibrium equations. In other words, the system is not statically determinateApprox. for small angles:Equilibrium: Fyf+Fyr1=Fyr2 and Fyf*lf+Fyr2*lr=0 Compatibility: (αr1+αr2)*lf/lr+αr1=δf -αf Constitutive relations: F yf =C αf *αfF yr1=C αr1*αr1F yr2=C αr2*αr2C α = cornering stiffness [N/rad]Together,3 eqs and 3 unknowns (the three slip angles) can be obtained for the figure below. Note that we assume a lateral force vector at each axle by choosing a slip angle:C αf *αf - C αr1*αr1 + C αr2*αr2 = 0 (Sum of forces in Y direction) C αf *αf *lf - C αr2*αr2*lr= 0 (sum of moments about r1) (αr1+αr2)*lf/lr + αr1 = δf - αf (compatibility)Steady state cornering at high speedIn a steady state curve at high speed, centripetal forces are needed to keep the vehicle on the curved track. Where do we find them? How large must these be? How are they developed in practice?Same C α at all axlesTest, e.g. prescribe steering angle. Calculate slip angles:VfThe centripetal force = F c=m*R*Ω2= m*Vx2/R. It has to be balanced by the wheel/road lateral contact forces:Equilibrium: Fyf+Fyr = F c = m*Vx2/R and Fyf*b-Fyr*c=0(Why not Fyf*b-Fyr*c=I*dΩ/dt ??? )Constitutive equations: F yf=Cαf*αf and F yr=Cαr*αrCompatibility: tan(δ−αf)=(b*Ω+Vy)/Vx and tan(αr)=(c*Ω-Vy)/Vxeliminating Vy for small angles and using Vx=R*Ω: δ−αf+αr=L/RTogether, eliminate slip angles:Fyf=(lr/L)*m*Vx2/R and Fyr=(lf/L)*m*Vx2/Rδ−F yf/Cαf+F yr/Cαr=L/REliminate lateral forces:d = L/R +[(lr/L)/Caf - (lf/L)/Car] * m*Vx2/Rwhich also can be expressed as: δ = L/R + [Wf/Cαf - Wr/Cαr] *Vx2/(g*R)(Wf and Wr are vertical weight load at each axle, respectively.)Wf/Cαf - Wr/Cαr is called understeer gradient or coefficient, denoted K or K us and simplifies to: d = L/R + K *Vx2/(g*R)A more general definition of understeer gradient:Note that this relation between δ , R and Vx is only first order theory. (Why?) Study a 2 axle vehicle in a low speed turn. How do we find the steering angle needed to negotiate a turn at a given constant radius? How do the following quantities vary with steering angle and longitudinal speed:•yaw velocity or yaw rate, i.e. time derivative of heading angle•lateral accelerationFor a low speed turn:Needed steering angle: δ = L / R (not dependent of speed)Yaw rate: Ω = Vx / R = Vx * δ / L (prop. to speed and steering angle)Lateral acceleration: ay = Vx2 / R = Vx2 * δ / L (prop. to speed and steering angle) Since steering angle is the control input, it is natural to define “gains”, i.e. division by δ:Yaw rate gain = Ω/δ =Vx/LLateral acceleration gain: ay/δ = Vx2/LFor a high speed turn:δ = L/R + K *Vx2/(g*R)Yaw rate gain = Ω/δ =(Vx/R) / δ=Vx/(L + K *Vx2/g)Lateral acceleration gain: ay/δ = (Vx2/R) / δ= Vx2/(L + K *Vx2/g)These can be plotted vs Vx:What happens at Critical speed? Vehicle turns in an unstable way, even with steering angle=0.What happens at Characteristic speed? Nothing special, except that twice the steeringangle is needed, compared to low speed or neutral steering..How is the velocity of the centre of gravity directed for low and high speeds?See the differences and similarities between side slip angle for a vehicle and for a single wheel. Bosch calls side slip angle “floating angle”.Some (e.g., motor sport journalists) use the word under/oversteer for positive/negative vehicle side slip angle.Transient corneringNOTE: Transient cornering is not included in Gillespie. This part in the course is defined by the answer in this part of lecture notes. For more details than given on lectures, please see e.g. Wong.To find the equations for a vehicle in transient cornering, we have to start from 3 scalar equations of motion or dynamic equilibrium. Sketch these equations.vm*dV I*d NOTE: It will m*dv/dt (2D vector equation)We like to express them without introducing the heading angle, since we thenwould need an extra integration when solving (to keep track of heading angle). In conclusion, we would like to use “vehicle fixed coordinates”.But the torque equation is straight forward:m*dV y /dt=Fyr+Fxf*sin(δ)+Fyf*cos(δ)x /dt=Fxr+Fxf*cos(δ)-Fyf*sin(δ)Ω/dt= -Fyr*c+Fxf*sin(δ)*b+Fyf*cos(δ)*bv is a vector. Let F also be vectors.NOT be correct if we only consider each component of v (Vx and Vy)separately, like this:=ΣF equation )I*d Ω/dt = ΣMz (1D scalar would like to express all equations as scalarequations . We would alsoMotion of a body on a plane surface:If we consider a rigid body (like a car) travelling on the road, we can analyse the motion of a reference frame attached to the vehicle.The body fixed to the x,y axes start with an orientation θ relative to the Global (earth fixed)system. The body has velocities V x and V y in the x,y system. Relative to the x,y system the point P has velocities:Ω−=y Vx vxΩ+=x Vy vyat time t t δ+, the velocities for P are:)()(Ω+Ω−+=′δδy Vx Vx x v )()(Ω+Ω++=′δδx Vy Vy y vSince the velocities have rotated by the angle δθ, the transformation of the velocities for P at time t t δ+to the original orientation:Time t+YTime tδ t)cos()sin()sin()cos(δθδθδθδθy v x v y v y v x v x v t t ′+′=′′−′=′where subscript “t” refers to coordinate system at time tThe difference of velocities for P in the time interval will then bevyy v vy vx x v vx −′=−′=δδSubstituting the values above:[][]()[][]()Ω+−Ω+Ω+++Ω+Ω−+=Ω−−Ω+Ω++−Ω+Ω−+=x Vy x Vy Vy y Vx Vx vy y Vx x Vy Vy y Vx Vx vx )cos()()()sin()()()sin()()()cos()()(δθδδδθδδδδθδδδθδδδIf consider that t δis very small, then )cos(δθ=1 and )sin(δθ=δθ and divide by t δtVy t x t y t y t Vx t Vx t vy t x t x t Vy t Vy t y t Vx t vx δδδδδδθδδδδδθδδδδδδδθδδδθδδθδδδθδδδδδδ+Ω+Ω−ΩΩ−+Ω=Ω−Ω−−−Ω−=()()()(if we let t=0 and let the global and local coordinate systems align at t=0 we can write dtd t ()()=δδ. We can also defineΩ=tδδθand ignore the second order terms ()()δδ⋅:22Ω−Ω+Ω+=Ω−Ω−Ω−=y dtd x Vx dt dVy ay x dtd y Vy dt dVx axAnd at the center of x,y system x=0, y=0:Ω+=Ω−=Vx dtdVyay Vy dtdVxaxNow, it will be correct if:m*a x = m*(dVx/dt - Vy*Ω) = Fxr + Fxf*cos(δ) - Fyf*sin(δ) m*a y = m*(dVy/dt + Vx*Ω)=Fyr + Fxf*sin(δ) + Fyf*cos(δ) I*d Ω/dt = - Fyr*c + Fxf*sin(δ)*b + Fyf*cos(δ)*bTry to understand the difference between (ax,ay) and (dVx/dt,dVy/dt).[The quantities (ax,ay) are accelerations, while (dVx/dt,dVy/dt) are “changes in velocities”. The driver will have the instantaneous feel of mass forces according to (ax,ay) but he will get the visual input over time according to (dVx/dt,dVy/dt).][Example: If going in a curve with constant longitudinal speed with driver in vehicle centre of gravity: The driver feel only “ax=0 and ay=centrifugal force=radius*Ω*Ω“ in his contact with the seat. However, he sees no changes in the velocity with which outside objects move, i.e. “dVx/dt=0 and dVy/dt=ay-Vx*Ω=radius*Ω*Ω-radius*Ω*Ω=0“.]Constitutive equations: F yf=Cαf*αf and F yr=Cαr*αrCompatibility: tan(δ−αf)=(b*Ω+V y)/V x and tan(αr)=(c*Ω-V y)/V xEliminate lateral forces yields:m*(dV x/dt - V y*Ω) = F xr + F xf*cos(δ) - Cαf*αf*sin(δ)m*(dV y/dt + V x*Ω) = Cαr*αr + F xf x*sin(δ) + Cαf*αf*cos(δ)I*dΩ/dt = -Cαr*αr*c + Fxf*sin(δ)*b + Cαf*αf*cos(δ)*bEliminate slip angles yields (a 3 state non linear dynamic model):m*(dV x/dt - V y*Ω) = Fxr + Fxf*cos(δ) - Cαf*[δ−atan((b*Ω+V y)/V x)]*sin(δ)m*(dV y/dt + V x*Ω) = Cαr*atan((c*Ω-V y)/V x) + Fxf*sin(δ) + Cαf*[δ−atan((b*Ω+V y)/V x)]*cos(δ) I*dΩ/dt = -Cαr*atan((c*Ω-V y)/V x)*c + Fxf*sin(δ)*b + Cαf*[δ−atan((b*Ω+V y)/V x)]*cos(δ)*b For small angles and dV x/dt=0 (V x=constant) and small longitudinal forces at steered axle (here Fxf =0), we get the 2 state linear dynamic model:m*dV y/dt +[(Cαf+Cαr)/V x]*V y + [m*V x+(Cαf*b-Cαr*c)/V x]*Ω=Cαf*δI*dΩ/dt +[(Cαf*b-Cαr*c)/V x]*V y + [(Cαf*b2+Cαr*c2)/V x]*Ω =Cαf*b*δThis can be expressed as:What can we use this for?- transient response (analytic solutions)- eigenvalue analysis (stability conditions)If we are using numerical simulation, there is no reason to assume small angles. Response on ramp in steering angle:• True transients (step or ramp in steering angle, one sinusoidal, etc.) (analysed in time domain) • Oscillating stationary conditions (analysed i frequency domain, transfer functions etc., cf. methods in the vertical art of the course).Examples of variants? Trailer (problem #2), articulated, 6x2/2-truck, all-axle-steering, ...ExampleShow that critical speed for a vehicle is sqrt(-L*g/K), using the differentialequation system valid for transient response. Assume some numerical vehicle parameters. Which is the mode for instability (eigenvector, expressed in lateral speed and yaw speed)?How to find global coordinates? dX/dt=Vx*cos ψ - Vy*sin dY/dt=Vy*cos ψ + Vx*sin X (global,Y (global,earth fixed) earth fixed)heading angle, Vx VyΩSolution sketch (using Matlab notation):» [m I g L l Cf/1000 Cr/1000] = 1000 1000 9.8 3 1.5 100000 80000(These are the assume vehicle parameters in SI units)» K=m*g/2*(1/Cf-1/Cr) = -0.0122 (understeer coefficient)» A=[m 0;0 I] =1000 00 1000 (mass matrix)» Vx=sqrt(-L*g/K)= 48.9898 (critical speed according to formula)» B=-[(Cf+Cr)/Vx m*Vx+(Cf*l-Cr*l)/Vx ;(Cf*l-Cr*l)/Vx (Cf*l*l+Cr*l*l)/Vx];» C=inv(A)*B; [V,D]=eig(C)0.9973 0.9864-0.0739 0.1644D = (diagonal elements are eigenvalues)0.0000 00 -11.9413Note that the first eigenvalue is zero, which means border between stability and instability. This is the proof!The eigenvector is first column of V, i.e. Vy=0.9973 and Ωz=-0.0739 (amplitudes):ExampleVehicles that have lost their balance might sometimes be stabilized through one-sided brake interventions on individual wheels (ESP systems). Which wheels and how much does one have to brake in the following situation?Vx=30 m/s, cornering radius=100 m.Before time=0: Cf=Cr=100000 /radAt time=0, the vehicle loses its road grip on the front axle, which can be modelled as a sudden reduction of cornering stiffness to 50000 N/rad.Assume realistic (and rather simplifying!) vehicle parameters.Solution (very brief and principal):Assume turning to the right, i.e. right side is inner side. Use the differential equation system for transient vehicle response, but add a term for braking m*dV y /dt + [(C αf +C αr )/V x ]*V y + [m*V x +(C αf *b-C αr *c)/V x ]*Ω=C αf *δ I*d Ω/dt + [(C αf *b-C αr *c)/V x ]*V y + [(C αf *b 2+C αr *c 2)/V x ]*Ω =C αf *b*δ ++ Mzwhere Mz=Fr*B/2, Fr=brake forces at the two right wheels, B=track width For t<0: Solve the eqs with dV y /dt = d Ω/dt = Mz=0 and Cf=Cr=100000 and Ω=Vx/radius=30/100 rad/s. This gives values of δ and Vy.For t=0: Insert the resulting values for δ and Vy into the same equation system but with Cf=50000 and do not constrain Mz to zero. Instead calculate Mz, which gives a certain brake force on the two right wheels, Fr.Check whether Fr is possible or not (compare with available friction, µ*normal force). If possible, put most of Fr on the rear wheel since front axle probably has the largest risk to drift outwards in the curve.Longitudinal & lateral load distribution during corneringWhen accelerating, the rear axle will have more vertical load. Explore what happens with the cornering characteristics for each axle. Look at Gillespie, fig 6.3. ...C Part of: Gillespie, fig 6.3o r n e r i n g s t i f f n e s sVertical loadSo, the cornering stiffness will increase at the rear axle and decrease at front axle, due to the longitudinal vertical load distribution during acceleration. This means lesstendency for the rear to drift outwards in a curve (and increased tendency for front axle) when accelerating.The opposite reasoning applies for braking (negative acceleration.)So, longitudinal distribution of vertical loads influence handling properties.NOTE: A larger influence is often found from the combined longitudinal and lateral slip which occurs due to the traction force needed to accelerate.In a curve, the outer wheels will have more vertical load. Explore what happens with the lateral force on an axle, for a given slip angle, if vertical load is distributed differently toSo, lateral distribution of vertical loads influence handling properties.How to calculate the vertical load on inner and outer side wheels, respectively, when the vehicle goes in a curve?First consider the loads on the vehicle body and axle:Force in Springs)(x x Ks Fi ∆+=, )(x x Ks Fo ∆−= where x is the static displacement of the springand Dx is the change in spring length due to body rollSum moments about chassis CGM sx x Ks s x x Ks =∆−−∆+2)(2)(2φs x =∆M K sKs ==φφ2where K φ is the roll stiffness for the axleMoment applied from body to axle=K φ φIf we take the sum of the moments about point A:ΣM A =00222=++−φφK hr RV m t Fzi t FzoThis simplifies to:02)(2=+=−φφK hr RV m t Fzi Fzo022)(2=+=−tK t hr R V m Fzi Fzo φφwe can define the term ∆Fz as∆Fz= (Fzo-Fzi)/2where ∆Fz is where the change of vertical load for each tire on the axleHow can we account for the whole vehicle? If we assume that the chassis is rigid, we can assume that it rotates around the roll centers for each axle. This is shown in the figure below:Roll moment about x axis M φ = {mV 2/R h 1 cos(φ) + mg h 1 sin(φ)} cos(ε)for small angles• M φ = mV 2/R h 1 + mg h 1 φ– Let W=mg• M φ = W h 1 (V 2/Rg+ φ)• If we know M φ = M φf+ M φr• M φ = (K φf +K φr )φthen:(K φf +K φr )φ= W h 1 (V 2/Rg+ φ)(K φf +K φr - W h 1 ) φ= W h 1 V 2/Rg)(121Wh K K Rg VWh r f −+=φφφThis is the roll angle based on the forward speed and curve radius.From previous expression for one axle2∆Fz= 2mV 2/R hr/t + 2K φ φ/twhere hr is the roll axis height. For front axle, Substitute the value the following into the previous equation.For front axle: mV 2/R=Wf/gV 2/RThis results in the relationship: )(11212Wh K K Rg V Wh t K t h Rg V W F r f f f f Zf −+⋅+⋅=∆φφφSimilarly for rear axle:)(11212Wh K K Rg V Wh t K t h Rg V W F r f r r r Zr −+⋅+⋅=∆φφφThese equations allow the exact load on each tire to be calculated. Then the cornering stiffness can be calculated if a functional relationship is known between the cornering stiffness C α and Fz.How is vertical load distributed between front/rear, if we know distribution inner/outer?It depends on roll stiffness at front and rear. Using an extreme example, without any roll stiffness at rear, all lateral distribution is taken by the front axle. .In a more general case:Mxf=kf*φ Mxr=kr*φ , where kf and kr are roll stiffness and φ=roll angle.Eliminating roll angle tells us that Mxf=kf/(kf+kr)*Mx and Mxr=kr/(kf+kr)*Mx, i.e. the roll moment is distributed proportional to the roll stiffness between front and rear axle. We can express each Fz in m*g, ay, geometry and kf/kr. This is treated in Gillespie, page 211-213.How would the diagrams in Gillespie, fig 6.5-6.6 change if we include lateral load distribution in the theory?It results in a new function =func(Vx), (eq 6-48 combined with 6-33 and 6-34). It could be used to plot new diagrams like Gillespie, fig 6.5-6.6:Equations to plot these curves are found in Gillespie, pp 214-217. Gillespie uses the non linear constitutive equation: Fy=Cα*α where Cα=a*Fz-b*Fz2 .What more effects can change the steady state cornering characteristics for a vehicle at high speeds?See Gillespie, pp 209-226: E.g. Roll steer and tractive (or braking!) forces. Braking in a curve is a crucial situation. Here one analyses both road grip, but also combined dive and roll (so called warp motion).Try to think of some empirical ways to measure the curves in diagrams in Gillespie, fig 6.5-6.6.See Gillespie, pp 27-230:Constant radius• Constant speed• Constant steer angle (not mentioned in Gillespie)How to calculate the vertical load on front and rear axles, respectively, when the vehicle accelerates?In general: ΣFz=mg and ΣFz,rear=mg/2+(h/L)*m*ax, where L=wheel base and h=centre of gravity height. ax=longitudinal acceleration. Still valid for braking because ax is then negative.Component CharacteristicsPlot a curve for constant side slip angle, e.g. 4 degrees, in the plane of longitudinal force and lateral force. Do the same for a constant slip, e.g. 4%. Use Gillespie, fig 10.22 as input.See Gillespie Fig 10.23Summary•low speed turning: slip only if non-Ackermann geometry•steady state cornering at high speeds: always slip, due to centrifugal acceleration of the mass, m*v2/R•transient handling at constant speed: always slip, due to all inertia forces, both translational mass and rotational moment of inertia•transient handling with traction/braking: not really treated, except that the system of differential equations was derived (before linearization, when Fx anddVx/dt was still included)•load distribution, left/right, front/rea r: We treated influences by steady state cornering at high speeds. Especially effects from roll moment distribution.Recommended exercise on your own: Gillespie, example problem 1, p 231. (If you try todetermine “static margin”, you would have to study Gillespie, pp 208-209 by yourself.)。
