下载文档原格式
第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一，它指出：自然界中的一切物质都具有能量，能量不可能被创造，也不能被消灭；但能量可以从一种形态转变为另一种形态，且在能量的转化过程中能量总量不变。
热力学第一定律是能量守恒与转换定律在热现象中的应用。
它确定了热力过程中热力系统与外界进行能量交换时，各种形态能量数量上的守恒关系。
一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。
它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能，故又称内能。
内动能取决于分子热运动，是温度的函数，而内位能取决于分子间的距离，是比体积的函数，即u = f ( T, v )二、总能除热力学能外，工质的总能量还包括工质在参考坐标系中作为一个整体，因有宏观运动速度而具有动能、因有不同高度而具有位能。
前一种能量称之为内部储存能，后两种能量则称之为外部储存能。
我们把内部储存能和外部储存能的总和，即热力学能与宏观运动动能和位能的总和，叫做工质的总储存能，简称总能。
即p k E U E E =++ （2-1）E---总能； U---热力学能； E k ---宏观动能； E p ---宏观位能。
第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现，为了简化公式和计算，把它定义为焓，用符号H 表示，即H=U+pV （2-2）1kg工质的焓值称为比焓，用h表示，即h=u+pv （2-3）焓的单位是J，比焓的单位是J/kg。
焓是一个状态参数，在任一平衡状态下，u、p和v都有一定得值，因而焓h也有一定的值，而与达到这一状态的路径无关。
当1kg工质通过一定的界面流入热力系统时，储存于它内部的热力学能当然随着也进入到系统中，同时还把从外部功源获得的推动功pv带进了系统。
因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和（u+pv），即比焓。
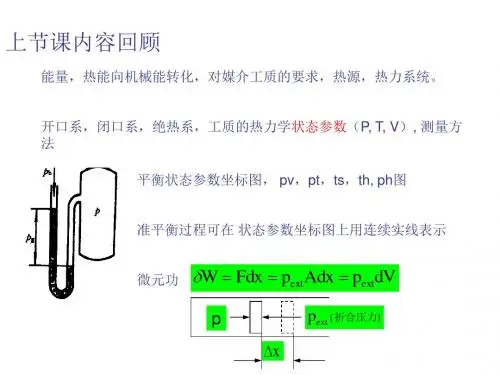
第二章 热力学第一定律主要公式及使用条件1. 热力学第一定律的数学表示式W Q U +=∆或 'a m b δδδd δd U Q W Q p V W=+=-+ 规定系统吸热为正，放热为负。
系统得功为正，对环境作功为负。
式中 p amb 为环境的压力，W ’为非体积功。
上式适用于封闭体系的一切过程。
2.焓的定义式3. 焓变（1） )(pV U H ∆+∆=∆式中)(pV ∆为pV 乘积的增量，只有在恒压下)()(12V V p pV -=∆在数值上等于体积功。
（2） 2,m 1d p H nC T ∆=⎰ 此式适用于理想气体单纯pVT 变化的一切过程，或真实气体的恒压变温过程，或纯的液体、固体物质压力变化不大的变温过程。
4.热力学能(又称内能)变 此式适用于理想气体单纯pVT 变化的一切过程。
5. 恒容热和恒压热V Q U =∆ (d 0,'0V W == p Q H =∆ (d 0,'0)p W ==6. 热容的定义式（1）定压热容和定容热容pVU H +=2,m 1d V U nC T ∆=⎰δ/d (/)p p p C Q T H T ==∂∂δ/d (/)V V V C Q T U T ==∂∂（2）摩尔定压热容和摩尔定容热容,m m /(/)p p p C C n H T ==∂∂,m m /(/)V V V C C n U T ==∂∂上式分别适用于无相变变化、无化学变化、非体积功为零的恒压和恒容过程。
（3）质量定压热容（比定压热容）式中m 和M 分别为物质的质量和摩尔质量。
（4） ,m ,m p V C C R -=此式只适用于理想气体。
（5）摩尔定压热容与温度的关系23,m p C a bT cT dT =+++式中a , b , c 及d 对指定气体皆为常数。
（6）平均摩尔定压热容21,m ,m 21d /()Tp p T C T T T C =-⎰7. 摩尔蒸发焓与温度的关系21vap m 2vap m 1vap ,m ()()d T p T H T H T C T ∆=∆+∆⎰ 或 v a p m v a p (/)p p H T C ∂∆∂=∆式中 vap ,m p C ∆ = ,m p C (g) —,m p C (l)，上式适用于恒压蒸发过程。
热力学第一定律对理想气体的应用
热力学第一定律（也称为能量守恒定律）对理想气体的应用提供了重要的物理洞察和计算方法。
以下是热力学第一定律在理想气体中的一些应用：
1.内能变化计算：热力学第一定律表明，理想气体的内能变化等于吸收的热量减去对外界做的功。
根据该定律，我们可以计算理想气体的内能变化，即ΔU = Q - W，其中ΔU 表示内能变化，Q 表示吸收的热量，W 表示对外界做的功。
2.等容过程计算：等容过程是指理想气体在体积不变的条件下发生的过程。
根据热力学第一定律，对于等容过程，ΔU = Q，即内能变化等于吸收的热量。
这使得我们可以根据所吸收的热量计算内能的变化。
3.等压过程计算：等压过程是指理想气体在恒定压力下发生的过程。
根据热力学第一定律，对于等压过程，Q = ΔU + W，即吸收的热量等于内能变化加上对外界所做的功。
这使得我们可以根据所做的功和内能变化计算吸收的热量。
4.等温过程计算：等温过程是指理想气体在恒定温度下发生的过程。
根据热力学第一定律，对于等温过程，Q = W，即吸收的热量等于对外界所做的功。
这意味着在等温过程中，吸收的热量和所做的功相等。
第二章热力学第一定律及其应用
1. 如果一个体重为70kg的人能将40g巧克力的燃烧热(628 kJ) 完全转变为垂直位移所要作的功 ,那么这点热量可支持他爬多少高度?
2. 在291K和下,1 mol Zn(s)溶于足量稀盐酸中,置换出1 mol H2并放热152 kJ。
若以Zn和盐酸为体系，求该反应所作的功及体系内能的变化。
3．理想气体等温可逆膨胀，体积从V1胀大到10V1，对外作了41.85 kJ的功，体系的起始压力为202.65 kPa。
(1)求V1。
(2)若气体的量为2 mol ,试求体系的温度。
4．在101.325 kPa及423K时，将1 mol NH3等温压缩到体积等于10 dm3, 求最少需作多少功？
（1）假定是理想气体。
（2）假定服从于范德华方程式。
已知范氏常数a=0.417 Pa·m6·mol-2, b=3.71× m3/mol.
5．已知在373K和101.325 kPa时，1 kg H2O（l）的体积为1.043 dm3,1 kg水气的体积为1677 dm3,水的 =40.63 kJ/mol 。
当1 mol H2O(l),在373 K 和外压为时完全蒸发成水蒸气时，求
（1）蒸发过程中体系对环境所作的功。
（2）假定液态水的体积忽略而不计，试求蒸发过程中的功，并计算所得结果的百分误差。
（3）假定把蒸汽看作理想气体，且略去液态水的体积，求体系所作的功。
（4）求（1）中变化的和。
（5）解释何故蒸发热大于体系所作的功？
6．在273.16K 和101.325 kPa时,1 mol的冰熔化为水，计算过程中的功。
已知在该情况下冰和水的密度分别为917 kg·m-3和1000 kg·m-3。
7．10mol的气体（设为理想气体），压力为1013.25 kPa,温度为300 K，分别求出等温时下列过程的功：
（1）在空气中（压力为101.325 kPa）体积胀大1 dm3。
（2）在空气中膨胀到气体压力也是101.325 kPa。
（3）等温可逆膨胀至气体的压力为101.325 kPa。
8．273.2K，压力为5×101.325 kPa的N2气2 dm3,在外压为101.325 kPa下等温膨胀，直到N2气的压力也等于101.325 kPa为止。
求过程中的W,ΔU ，ΔH 和Q。
假定气体是理想气体。
9．0.02kg乙醇在其沸点时蒸发为气体。
已知蒸发热为858kJ/kg.蒸汽的比容为0.607 m3/kg。
试求过程的ΔU ，ΔH，Q，W（计算时略去液体的体积）。
10. 1× kg水在373K，101.325 kPa压力时，经下列不同的过程变为373 K，
压力的汽，请分别求出各个过程的W，ΔU ，ΔH 和Q 值。
（1）在373K，101.325 kPa压力下变成同温，同压的汽。
（2）先在373K，外压为0.5×101.325 kPa下变为汽，然后加压成373K，101.325 kPa压力的汽。
（3）把这个水突然放进恒温373K的真空箱中，控制容积使终态为101.325 kPa 压力的汽。
已知水的汽化热为2259 kJ/kg。
11. 一摩尔单原子理想气体，始态为2×101.325 kPa,11.2 dm3,经pT=常数的可逆过程压缩到终态为4×101.325 kPa，已知C(V,m)=3/2 R。
求：
（1）终态的体积和温度。
（2）ΔU 和ΔH 。
（3）所作的功。
12．设有压力为101.325 kPa，温度为293K的理想气体3 dm3,在等压下加热，直到最后的温度为353K为止。
计算过程中W，ΔU ，ΔH 和Q。
已知该气体的等压热容为C(p,m)=(27.28+3.26·
T) J/(K·mol)。
13. 在标准压力下，把一个极小的冰块投入0.1 kg,268 K(即-5 ℃)的水中，结果使体系的温度变为273 K，并有一定数量的水凝结成冰。
由于过程进行的很快，可以看作是绝热的。
已知冰的溶解热为333.5 kJ/kg,在268-273K之间水的比热为4.21 kJ/(K·kg)。
（1）写出体系物态的变化,并求出ΔH.
（2）求析出冰若干克。
14．一摩尔氢在298.2 K和压力101.325 kPa下经可逆绝热过程压缩到5 dm3,计算：
（1）氢气的最后温度。
（2）氢气的最后压力。
（3）需做多少功。
15．某一热机的低温热源为313 K，若高温热源分别为
（1） 373K，（在101.325 kPa下水的沸点）
（2） 538K，（是压力为50×101.325 kPa下水的沸点）。
试分别计算热机的理论换算系数。
16. 某电冰箱内的温度为273 K，室温为298K，今欲使1 kg 273 K的水变成冰，问最少需做多少功？已知273 K时冰的融化热为335kJ/kg 。
17. 0.500 g正庚烷放在弹形量热计中，燃烧后温度升高2.94 K。
若量热计本身及其附件的热容量为8.177kJ/K, 计算298K时正庚烷的燃烧热（量热计的平均温度为298 K）。
18. 在298.15K及101.325 kPa压力时设环丙烷，石墨及氢气的燃烧热（）
分别为-2029，-393.8及-285.84 kJ/mol。
若已知丙烯（气）的=20.5 kJ/mol，试求：
（1）环丙烷的。
（2）环丙烷异构化变为丙烯的。
19. 某高压容器中含有未知气体，可能是氮或氩气。
今在298 K时，取出一些样品，从5 dm3绝热可逆膨胀到6 dm3,温度降低了21 K，试问能否判断出容器中是何种气体？
设振动的贡献可忽略不计。
20. 将H2O看作刚体非线性分子，用经典理论来估计其气体的C(p,m)值是多少？
如果升高温度，将所有振动项的贡献都考虑进去，这时C(p,m)值又是多少？。
