等式的基本性质.2 等式的基本性质
- 格式:ppt
- 大小:938.00 KB
- 文档页数:35




等式的基本性质1和2和3
等式是一种数学表达形式,被广泛用于求解数学问题和描述数学概念。
因此,了解等式的基本性质对于掌握数学非常重要。
首先,对等比数列性质1,当两个等式中的各项有相等的成比例关系时,这两个等式就叫做等比数列。
例如:式中x:2;y:4,则x:y=2:4,这叫做等比。
其次,性质2为线性性质,当一个等式中的各项按一定的线性关系分布时,它就叫做线性方程式。
例如:式中x:3;y:2,则x:y=3:2,这就叫做线性的。
最后,等式的性质3为一致性质,当两个等式中的术语完全相同时,这两个等式就叫做一致的。
例如:式中x:2;y:2,则x=y,这就叫做一致。
综上所述,等式的基本性质包括等比性质、线性性质和一致性质。
掌握等式的基本性质,对把握数学原理、解决数学问题有重要意义,也是数学学习的基础。



一、等式的基本性质等式基本性质1:等式两边同时加上同一个数或减去同一个数,等式仍成立; 即如果A =B ,那么A ±m =B ±m .等式基本性质2:等式两边同时乘以同一个数或除以同一个不等于零的数,等式仍成立;即如果A =B ,那么Am =Bm 或A Bn n=(m 、n 为两个数,n ≠0).二、一元一次方程(1) 方程:含有未知数的等式;如:37x +=,2113a b+=,326255p q +=,… (2) 一元一次方程:含有一个未知数,并且未知数的指数是1的方程;如:37x +=,71539q +=,214682m+=,… (3) 一元一次方程的解:能使一元一次方程左右两边相等的未知数的值;如:4x =是方程37x +=的解,247q =是方程71539q +=的解,… 三、二元一次方程(组)(1) 二元一次方程:含有两个未知数,并且未知数的指数均为1的方程;如:2318x y +=,713mn =-,… (2) 二元一次方程组:把具有相同未知数的两个二元一次方程合在一起组成的方程组;如:58335x y x y +=⎧⎨+=⎩,27322a bb -⎧=⎪⎨⎪=⎩,…(3) 二元一次方程的解:适合于一个二元一次方程的每一对未知数的值,叫作二元一次方程的一个解;经典精讲第五讲列方程解应用题如:62xy=⎧⎨=⎩是2318x y+=的一个解;12173xy⎧=⎪⎪⎨⎪=⎪⎩也是2318x y+=的一个解;…(4)二元一次方程组的解:满足方程组中每一个方程的解就是这个方程组的解;如:41xy=⎧⎨=⎩是58335x yx y+=⎧⎨+=⎩的解;…(5)解二元一次方程组的方法:代入消元法、加减消元法四、不定方程(组)不定方程(组):当未知数的个数多于方程个数的方程(组),我们称其为不定方程(组)1.一般情况下求不定方程的特殊解,首先要估算未知数的取值范围,一般从系数较大的进行估算2.当不定方程的系数含有5时,用个位数字特征解题较为方便,如果可以结合奇偶分析的话,还可以确定出个位数字的具体数值3.对于其他系数的,完全都可以根据等式两边除以某个未知数系数的余数相同来解丙看到甲、乙两人正在解下面这个方程组:x y x y +=⎧⎨+=⎩2536 704W WW W,其中未知数前面的系数被甲和乙遮住了.甲计算得出方程的解是x=7,y=3;而乙误把“2536”看作“1536”,得到的解是x=4,y=4.试问:方程组四个被遮住的系数中最小的一个是多少?按要求解下列方程(1)372041027x y zx y z++=⎧⎨++=⎩,求x y z++的值。

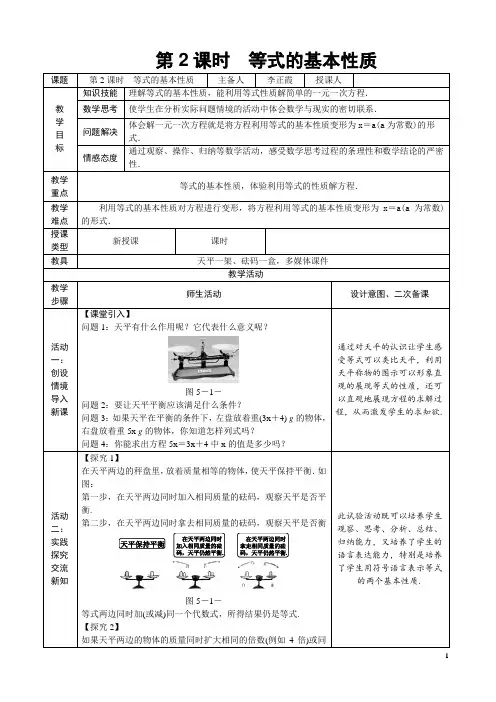

等式的基本性质教学内容:数学书P55-56及“做一做”。
教材首先提出问题:同学们,你用天平做过游戏吗?引起学生的探究兴趣。
然后通过四幅插图描绘了利用天平进行实验,探究等式基本性质的过程。
前两幅图描绘在天平的两边同时放上或拿走同样的物品,天平仍然平衡。
这实际上揭示了等式的一条基本性质:等式两边加上或减去相等的数,等式不变。
后两幅图描绘了把天平两边的物品翻倍或只取它的几分之一,天平保持平衡。
这实际上揭示了等式的另一条基本性质,即等式两边同时乘或除以相同的数(0除外),等式不变。
这几幅连环画式的插图,一方面提示教师可以怎样演示,另一方面也给学生思考、感悟天平保持平衡的变化规律,提供了直观的观察材料。
有必要指出,教具演示能使学生看到动态的过程,获得实实在在的真切感受。
但演示过后,出现在学生眼前的,只剩最后的结果状态。
而连环画式的插图,没有实物演示那么生动,但可以保留初始状态和结果状态,便于学生观察、比较前后什么变了、什么不变。
为了减轻学生的记忆负担,教材没有出现“等式基本性质”的名称,也不给出概括性质的文字。
这是因为,在本单元中,等式的基本性质(称之为“天平保持平衡的道理” ),只是作为解方程的认知基础。
教学目标:1. 通过天平演示保持平衡的几种变换情况,让学生初步认识等式的基本性质。
2. 利用观察天平保持平衡所发现的规律能直接判断天平变化后能否保持平衡。
3. 培养学生观察与概括.比较与分析的能力。
重点难点:理解,并能用自己的话来阐述天平保持平衡的几种变换情况,进而发现等式保持不变的规律。
教具准备:天平及相关物品。
(也可以将插图制作成课件让学生逐步观察思考)教学方法:教学时,可以先按课本提示设问、再开始演示。
也可以先让学生观察天平左边放上茶壶,右边放上两个杯子,保持平衡。
然后提问:怎样变换,能使天平仍然保持平衡呢?待学生思考片刻,再进一步提问:往两边各放1个杯子,天平会发生什么变化?学生回答后,教师通过演示加以验证,得出1个茶壶加1个杯子的质量等于3只杯子的质量。