平行束反投影重建
- 格式:doc
- 大小:1.54 MB
- 文档页数:19

反投影重建算法
反投影重建算法(FBP)是一种计算机断层扫描成像(CT)重建图像
的方法。
该算法基于通过旋转体与X射线束的物理原理,将多个方向
的X射线透射数据进行积分,并使用反投影算法将数据重构成一张图像。
FBP算法分为两个基本部分:投影操作和反投影操作。
投影操作是一
种从图像中提取片段的技术,而反投影操作则是将这些片段重构成图像。
FBP重建算法的本质是一种频域过滤操作,其通过滤波技术提取
图像中的高频信息,并使用反投影技术将其还原为一张二维图像。
反投影重建算法的主要优点是其速度和适应性。
这种算法能够轻松地
生成高质量的图像,并且对于许多不同的应用程序都可以使用不同的
滤波模式。
目前,FBP算法被广泛应用于医学成像、工业检测和材料
科学等领域。
需要注意的是,FBP算法并不是完美的。
由于其基于体积的积分,因
此它可能受到一个“锐角偏差”问题的影响。
锐角偏差问题是指,当
图像中存在锐利的边缘或角落时,算法可能会出现伪影或失真的问题。
为了应对这个问题,一些改进算法被提出,例如金刚簇算法(来自中
国科技大学),基于块的迭代顺序最小化算法和模糊模式匹配算法等。
总之,反投影重建算法是一种实用的成像算法,对于许多不同的领域都具有广泛的适用性。
虽然这种算法具有其局限性,但是通过改进算法可以进一步提高它的可靠性和精度。




反投影重建算法介绍反投影重建算法是一种常用于医学图像重建的技术,它通过将多个投影图像反向投影到空间中,来重建出原始物体的三维形态。
该算法基于X射线摄影和计算机图形学的理论,被广泛应用于医学成像领域,尤其是计算机断层扫描(CT)。
基本原理反投影重建算法的基本原理是通过测量某物体在不同角度下的投影数据,然后将这些数据反向投影到空间中,得到物体的三维重建图像。
具体步骤如下:1.采集投影数据:使用X射线或其他成像设备,获得物体在不同角度下的投影数据。
这些投影数据可以通过测量X射线的衰减程度来获取。
2.投影数据的逆变换:将投影数据的方向进行反转,得到反投影数据。
这一步是算法中最重要的一步,它将每个测量点的投影数据映射回三维空间。
3.反投影重建:将反投影数据从二维空间转换为三维空间。
这可以通过将反投影数据相加来实现。
在这个过程中,需要注意对数据进行插值,以确保重建图像的精确度。
算法细节反投影重建算法的具体细节有多种实现方式,下面列举几种常见的算法:1. 直接反投影算法直接反投影算法是一种最简单的算法,它将每个投影像素直接投影回三维空间。
具体步骤如下:1.对每个投影像素点,计算它在三维空间中的坐标。
这可以通过测量点在投影平面上的位置和投影矩阵来实现。
2.将每个投影像素点的坐标值累加到三维空间的相应位置上。
这一步是反投影的核心过程,通过将每个像素点的坐标值相加,最终可以得到物体的三维重建图像。
3.可选的后处理步骤:根据需要,可以对重建图像进行滤波、增强或其他处理,以提高图像的质量。
2. 迭代反投影算法迭代反投影算法是一种更复杂但更精确的算法,它通过多次迭代求解,逐渐优化重建图像的质量。
具体步骤如下:1.初始化重建图像:将重建图像的像素初始化为某一固定值。
2.迭代求解:重复以下步骤,直到算法收敛或达到最大迭代次数:–计算投影数据的理论值:根据当前重建图像,计算预测的投影数据。
–计算误差:比较预测的投影数据与实际测量数据之间的差异,得到误差。

ct 重建原理
ct重建原理是一种通过计算机对已获得的投影数据进行重组,以生成三维图像的技术。
该技术基于计算机断层扫描(computed tomography,CT)的原理,包括X射线的穿透与
吸收、探测器的信号检测与记录以及计算机的数据处理与重建等关键步骤。
整个过程首先通过X射线源发射一束平行的X射线,穿透被
检对象并与X射线接收器(探测器)发生相互作用。
被检对
象对X射线的吸收程度取决于其组织密度和厚度,吸收后的
X射线会引起探测器上的电离现象,通过记录探测器上的信号变化,可以获得大量的投影数据。
投影数据是表示被检对象在不同方向上的X射线吸收情况的
一系列数值,这些数据记录了X射线通过被检对象时的强度
衰减情况。
然后,计算机通过运算和重组这些投影数据,可以恢复出被检对象的内部结构信息,生成层叠的二维切片图像。
CT重建的核心原理是反投影算法。
反投影算法使用投影数据
和旋转角度信息,将投影数据“逆向投影”回原始空间中,并按照旋转角度进行叠加和插值计算,最终得到各个切片的像素灰度值。
然后,这些像素灰度值通过图像处理算法可呈现出清晰的可视化图像,形成我们所看到的三维结果。
CT重建原理的关键在于通过反投影算法将二维投影数据还原
为三维立体图像,并能够在图像上显示出被检对象的内部结构。
这种技术在医学、工业检测等领域具有广泛应用,可以提供精确的图像信息,帮助医生和研究人员做出更准确的诊断和分析。

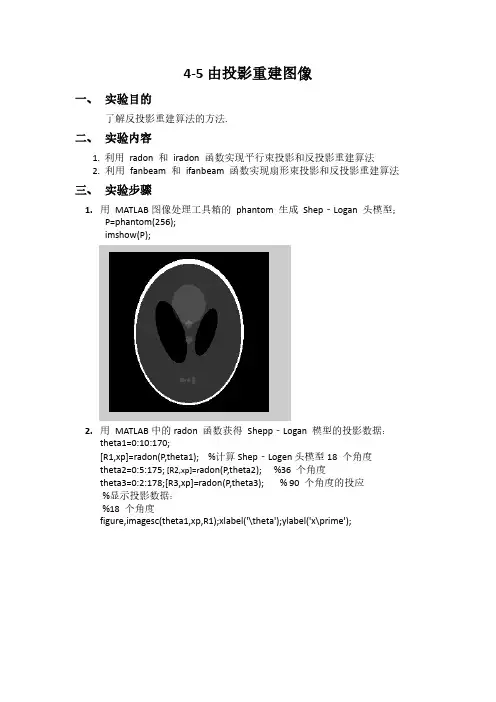
4-5 由投影重建图像一、 实验目的了解反投影重建算法的方法.二、 实验内容1.利用radon 和iradon 函数实现平行束投影和反投影重建算法2. 利用fanbeam 和ifanbeam 函数实现扇形束投影和反投影重建算法三、 实验步骤1.用MATLAB图像处理工具箱的phantom 生成Shep‐Logan 头模型;P=phantom(256);imshow(P);2.用MATLAB中的radon 函数获得Shepp‐Logan 模型的投影数据:theta1=0:10:170;[R1,xp]=radon(P,theta1); %计算Shep‐Logen头模型18 个角度theta2=0:5:175; [R2,xp]=r adon(P,theta2); %36 个角度theta3=0:2:178;[R3,xp]=radon(P,theta3); % 90 个角度的投应%显示投影数据:%18 个角度figure,imagesc(theta1,xp,R1);xlabel('\theta');ylabel('x\prime');% 36 个角度figure,imagesc(theta2,xp,R2);xlabel('\theta');ylabel('x\prime'); % 90 个角度figure,imagesc(theta3,xp,R3);xlabel('\theta');ylabel('x\prime');3.用MATLAB 中的iradon 函数对获得的投影数据进行滤波反投影重建,获得Shepp‐Logan 模型的重建图像:I1=iradon(R1,10);I2=iradon(R2,5);I3=iradon(R3,2);%显示重建图像:figure,imshow(I1);figure,imshow(I2);figure,imshow(I3);四、 实验总结本次实验内容较少,通过本次实验我了解了反投影重建算法的方法.了解了利用radon 和iradon 函数实现平行束投影和反投影重建算法。

CT图像重建技术CT图像重建技术000计算机层析成像(Computed Tomography,CT)是通过对物体进行不同角度的射线投影测量而获取物体横截面信息的成像技术,涉及到放射物理学、数学、计算机学、图形图像学和机械学等多个学科领域。
CT技术不但给诊断医学带来革命性的影响.还成功地应用于无损检测、产品反求和材料组织分析等工业领域。
CT技术的核心是由投影重建图像的理论,其实质是由扫描所得到的投影数据反求出成像平面上每个点的衰减系数值。
图像重建的算法有很多,本文根据CT扫描机的发展对不同时期CT所采用重建算法分别进行介绍。
第一代和第二代CT机获取一个单独投影的采样数据是从一组平行射线获取的,这种采样类型叫平行投影。
平行投影重建算法一般分为直接法与间接法两大类。
直接法是直接计算线性方程系数的方法,如矩阵法、迭代法等。
间接法是先计算投影的傅立叶变换,再导出吸收系数的方法,如反投影法、二维傅立叶重建法和滤波反投影法等[1]。
2.1 直接法2.1.1 矩阵法设一个物体的内部吸收系数矩阵为:(1)为了求得该矩阵中的元素值,我们可以先计算该矩阵在T个角度下的T组投影值 ,如设水平方向时 ,则:(2)同样其它角度下也有类似方程,把所有方程联立得到求解,即可求得所有u值。
通常情况下,由于联立方程组的数目往往不同于未知数个数,且可能有不少重复的方程,这样形成的不是方阵,所以一般不满秩,此时需要利用广义逆矩阵法进行求解。
2.1.2 迭代法实际应用中,由于图像尺寸较大,联立的方程个数较多,采用直接采用解析法难度较大,因此提出了迭代重建方法。
迭代法的主要思想是:从一个假设的初始图像出发,采用迭代的方法,将根据人为设定并经理论计算得到的投影值同实验测得的投影值比较,不断进行逼近,按照某种最优化准则寻找最优解[2]。
通常有两种迭代公式,一种是加法迭代公式[2]:(3)另一种是乘法迭代公式[2]:(4)两式中是相邻两次迭代的结果;是某一角度的实测投影值,是计算过程的计算投影值, 是投影的某一射线穿过点的点数,即计算投影值的射线所经过的像素的数目,是松弛因子。

一、断层成像的基本原理1.1 断层成像这样我们用数学方法解决了一个断层成像问题。
一般来说,断层成像都是用数学计算的手段解决的。
怪不得有CT (Computed Tomography 计算机断层成像,直译为:计算出的断层成像) 这个词。
通常为说话简捷起见,“计算出的”这几个字就略去不说了。
矩阵每一行的和,每一列的和的概念可以推广为一个图像的射线和,线积分,和投影数据。
从物体的投影数据来得到物体的内部断层成像的过程就称之为图像重建。
1.2 投影●为了体会出投影 (也就是射线和,线积分) 的概念,我们在这里给出几个例子。
●第一个例子:所考虑的物体是二维x-y平面中的一个均匀圆盘。
圆盘的圆心在坐标原点。
圆盘的线密度函数是个常数ρ (图1.4)。
●物体的投影值(即线积分值) 就是弦长 t 乘以线密度ρ。
●其数学表达式为:●在这个特例中,投影值 p(s) 对于所有的角度θ来说都是一样的。
这个角度θ是探测器相对于物体的旋转角度。
图 1.4 跨圆盘的线积分等于弦长乘以线密度图 1.5 物体的投影在不同的探测角度是不同的图1.7 投影值实际上是像素值的加权和。
权函数是“线”在像素内的线段长度。
1.3 图像重建●我们来探索重建一个点源的步骤及策略。
●这些步骤和策略可以推而广之,来解决一般的图像重建问题。
●我们首先在二维 x-y 坐标系中随便放一个点源。
点源的位置不一定要在坐标系的原点 (图1.8)。
我们设想有一个探测器绕着坐标系的原点旋转。
旋转角为θ。
这个探测器可以是架照相机。
探测器测到的投影数据为 p(s,θ),这里s是探测器上的一维坐标。
图 1.8 点源物体投影数据的采集计算投影数据●计算投影数据 p(s,θ),我们可以画出一条条垂直于探●测器的直线。
然后沿着这些直线对物体求线积分。
●对于点源物体,投影数据 p(s,θ) 可以简单地得到:●这只需在 x-y 平面上过该点源向探测器作一条垂线。
●这条垂线与探测器的交点位置 s 有一个高度为 1 的脉冲。

图像重建是CT技术的一个研究热点。
重建算法的现实是对算法研究的一个重要环节。
由Math Works公司推出的MATLAB工具软件具有强大的数学计算和图像处理功能,并为算法提供了
一个方便有效的研究和实现的平台。
本文在图像重建分析的基础上,运用MATLAB实现了基于扇
束的滤波反投影重建算法的计算机模拟。
引言
图像重建技术在诸多领域中发挥着重要作用,在重建算法的研究
和实现过程中,存在着是一系列极其复杂的图像处理问题和数学计算
图5 128×128的Sheep
Logan头模型图像
图6 扇束射角增量为0.3°投影值
2. 选取滤波函数,并离散化处理,如:R-L滤波函数,则离散化形式为:
(式1-8)其中:
(式1-9)
图7 重建效果图
总结
本文在分析基于扇束滤波反投影算法的基础上,详细介绍了该算法“模拟产生投影数据——修正投影——加权滤波——反投影重建”整个计算机现实过程,并充分利用Matlab强大的图像处理功能,无需大量的编程,现实了图像重建算法的计算机模拟。
高效的工程计算语言,它从本质上提供了对图像的支持,使用它可以对数字图像形成的离散数据矩阵进行一次性的处理,较其他高级语言。
CT断层图像重建算法研究专业:通信工程姓名:刘明帅指导教师:骆岩红摘要CT技术是一种融合了射线光电子学、信息学、微电子学等学科的新兴技术,因为其先进的无损检测技术,所以被广泛地应用于医学、航天、生物等多个领域。
随着科技的进步,图像重建技术开始应用于X射线中,这是数字图像处理的一个重大进步。
如何能重建出高质量的图像,取决于所采用的重建算法。
从图像重建的角度来看,主要分为解析法与迭代法。
解析法是利用解析、变换重建公式来构建重建图像。
它具有容易实现,速度较快,且能重建出高质量的图像的特点,但是对投影数据完备性要求高。
迭代法是利用求解线性方程组来重建图像,它能够在投影数据信噪较低条件下,获得高质量图像。
本文将从原理、应用、与优缺点的角度来分析两种算法,重点对解析法中的滤波反投影算法从平行束与扇束投影方式进行研究,最后通过Visual C++与MATLAB软件相结合的方式对图像重建,并分析各参数对重建图像的影响。
关键字:CT技术图像重建算法滤波反投影算法AbstractCT technology is a emerging technology that blend of the Ray optoelectronics, microelectronics and informatics subject. Because of its advanced nondestructive testing technology, it is widely used in medical, aerospace, biological and otherfields. With the progress of science and technology, Image reconstruction technology is applied to the X ray, This is a major progress of digital image processing. How to rebuild the high quality images, depends on the reconstruction algorithm you adopt. From the perspective of image reconstruction, it mainly divided into the analytical method and iteration method.Analytical method use the analysis and transform formula to build image reconstruction.It has the characteristics of implementating easily and fast,and reconstructing out high quality images,but the demand of the projection data is high. Iterative method is used to solve the linear system of equations to reconstruction image, the projection data under the condition of low signal-to-noise, it can get high quality image.This article we will be from the point of view of the principle ,application,and the advantages and disadvantages to analysis the two kinds of algorithms, focusing on studying the analytical method of filter back projection algorithm from the parallel beam and fan beam projection methods , finally, combining the software of Visual c + + with MATLAB software to image reconstruction, and analyzes the influence of various parameters on the reconstruction imageKey words: CT technology image reconstruction algorithmFiltered Backprojection Algorithm目录第一章绪论........................................................................................ - 6 -1.1 CT技术与图像重建概述 ...................................................... - 6 -1.2 CT和重建技术的发展及研究现状 ...................................... - 6 -1.3 研究的目的与意义 ............................................................... - 8 - 第二章 CT成像原理和图像重建算法 ................................................ - 9 -2.1 CT成像原理与系统组成 ........................................................ - 9 -2.2 CT成像系统扫描方式的发展 .............................................. - 10 -2.3 CT断层图像原理 .................................................................. - 11 -2.4图像重建算法概述 ................................................................ - 13 -2.4.1解析类方法 .................................................................. - 13 -2.4.2传统迭代类方法 .......................................................... - 13 - 第三章 CT图像重建算法实现原理的研究 ................................ - 14 -3.1图像重建系统中的数学概念及变换 .................................... - 14 -3.1.1 投影与反投影 ............................................................. - 14 -3.1.2 Radon变换及其反变换 .............................................. - 15 -3.1.3傅里叶变换 .................................................................. - 16 -3.1.4中心切片定理 .............................................................. - 16 -3.2解析类重建算法 .................................................................... - 17 -3.2.1直接傅里叶变换算法 .................................................. - 17 -3.2.2反投影重建算法 .......................................................... - 18 -3.3 迭代类重建算法 ................................................................... - 20 -3.3.1 代数迭代重建算法 ..................................................... - 21 -(1) ART算法 ...................................................................... - 21 -(2)同时代数重建算法 ....................................................... - 22 -3.3.2 影响代数迭代重建算法的因素 ................................. - 22 -3.3.3 ART重建算法与SART ................................................. - 25 -3.3.4 统计迭代重建算法 ..................................................... - 27 -(1)最小二乘图像重建算法 ............... 错误!未定义书签。
医学成像系统实验:X-CT图像重建实验目的:Sheep-Logan模型是由10个位置、大小、方向、密度各异的椭圆组成,用来模拟一个脑断层的图像。
通过该模型,可以获得各个投影方向上数据的解析表达式。
利用matlab产生Sheep-Logan模型的仿真投影数据,重建X-CT图像,从而理解图像重建算法。
实验内容:基本要求部分1.利用Sheep-Logan头部模型生成平行束投影。
本部分要求:写出平行束投影表达式,根据Sheep-Logan模型自行编程生成各个方向上投影离散数据,与matlab函数所生成的数据加以比较,充分理解X-CT 投影数据获得的过程。
2.根据平行束投影数据重建图像。
本部分要求:自行编写利用滤波反投影法、R-L函数卷积反投影法、S-L函数重建图像的程序,比较重建的效果,并与matlab提供的函数相比较,充分的理解平行束投影重建算法。
3.在重建过程中,引入噪声、检测器损坏、旋转中心偏移等问题,对重建的结果加以比较和探讨。
可获得免试资格的选做部分(仍选其一即可获得免试资格,根据完成的水平给与相当于期末考试的分数,多选多得分)1.扇形束重建:利用Sheep-Logan模型,根据扇形束投影的原理自行编程生成投影数据,与matlab函数比较;利用数据重排方法和直接加权反投影方法重建图像,比较效果;在重建过程中,同样引入一些误差来源加以分析;理解共轭采样对,分析重建所需的最小数据集。
2.三维螺旋X-CT仿真:自行生成一组重叠或者相套的椭球模型作为体数据,设计一组螺旋X-CT的参数(多排/单排、p=d/W),根据投影原理,生成一套投影数据,利用360°差值和180°差值重建若干个断面的图像,与仿真数据比较,分析重建效果;改变一些配置的参数,比较重建效果。
3.迭代重建算法:自行查阅文献,理解迭代中间算法的基本原理,根据投影数据实现迭代重建算法,与各类反投影算法加以比较,分析优、缺点。
89中国设备工程Engineer ing hina C P l ant中国设备工程 2019.12 (下)计算机断层扫描影像技术,简称CT 设备,广泛应用在医学影像诊断、工业无损检测、生物技术等领域。
CT 技术通过对被扫描物体进行圆周扫描获得一系列投影数据后,再通过特定的图像重建算法重建出物体一层一层的CT 图像,清晰地获得物体内部结构信息,诸多层CT 图像罗列在一起又可形成直观的物体三维影像结构。
影响CT 设备成像精度的因素包括机械运动误差、温度环境、湿度环境、X 射线球管质量、探测器缺陷等,其中,探测器缺陷是影响CT 成像的重要因素,也是定期需要校正或更换的高精度高价值部件。
CT 设备中的探测器上布满紧密排列的探测元,探测元用于接收穿过成像物体后的剩余X 射线信号,是构成投影图像的基础。
探测器上探测元的损坏会造成重建出的CT 图像含有明显的环形伪影,其环形的粗细程度随着探测元损坏多少的变化而变化。
本文以CT 设备中探测器上探测元损坏作为问题点,从算法的角度对该问题提出行之有效的解决措施。
基金项目:广州市创新环境建设计划(201906010013);广州市创新环境建设计划(201906010014)。
通讯作者:齐洪亮。
CT 设备探测器损坏对图像重建质量的影响及解决方案胡洁,王浩文,齐宏亮(广州华端科技有限公司,广东 广州 510670)摘要:本文探讨了计算机X 射线断层影像设备(CT)探测器上含有坏损探测元时的图像重建质量改善方案。
对于发生损坏的探测元上的数据,利用其两侧正常工作的探测元上的数据进行插值估计,再使用基于滤波反投影的CT 图像算法重建得到修正后的图像。
分别模拟CT 设备探测器上的探测元少量坏死和多量坏死的情况,对校正前和校正后的CT 图像进行对比实验。
未经过算法校正的CT 图像含有明显的环形伪影,经过文中算法校正后的CT 图像几乎无环形伪影存在,保留了图像细节信息。
文章针对CT 设备中探测器上探测元损坏作为问题点提出了行之有效的方案,校正后的图像质量满足需求,同时降低了CT 设备高值元器件的更换成本。
一、 平行束反投影重建算法平行束 重建采用的是平移加旋转的扫描方式,如图所示,射线源在某一角度下水平移动,将物体全部照射后旋转一角度,如此重复,在这个过程中探测器相应地运动以接收X 射线。
1、反投影重建算法的物理概念: 断层平面中某一点的密度值可以看作是这一平面内所有经过该点的射线的投影值之和(的均值)。
整幅重建图像可以看作是所有方向下的投影累加而成。
射线标号示于图中,像素值(代表密度)分别1x ,2x ,3x ,4x ,赋值如下:15x =,20x =,32x =,418x =根据投影的定义(某条射线投影值为该条射线穿过的所有的像素值之和),每条射线的投影i p (1,2i =)为:1215p x x =+=, 23420p x x =+=,3137p x x =+= 42418p x x =+=, 532p x ==, 61423p x x =+=720p x ==根据反投影重建算法的物理意义,重建图像中各像素,得到:113635x p p p =++=,214723x p p p =++=, 323529x p p p =++=,424661x p p p =++=(a) 原图像像素值 (b)反投影重建后图像 (c)求平均后图像图 反投影示例重建后的图像如图(b)所示,可以看出原图像中像素值不为零的点反投影重建后仍较突出,但原图中像素值为零的点,经反投影重建后不再为零,即有伪迹。
有时为了使重建后图像的像素值更接近于原图的像素值,在求反投影时,把数据除以投影的数目(即射线数),图 平行束平移加旋转图 断层像素值和射线如图(c)所示。
因此有:,11pn k k ii px pn ==∑该式可作为反投影重建算法的计算式。
其中k x 表示像素k 的值,i k p ,表示经过像素k的第i 条射线投影,p n 表示图像内的射线条数。
图(a)表示空间中一个孤立点源A ,密度为1。
经过A 点的三条射线也示于图中。
射线束理论上可以很多,取三条示意。
不经过A 点的射线投影为零,经过A 点的射线投影值均为1,1231p p p ===。
(a) 孤立点源A 及三条射线 (b)相应的反投影重建图,有星状伪迹图 孤立点源的反投影重建及星状伪迹经反投影重建后,得到A 点的像素值为123()/31A f p p p =++=。
A 点以外的像素值原来为零,经反投影重建后不等于零,而是等于1/3。
所以,经反投影重建后的图像除保留A 点的像外,还有像素值为1/n 的灰雾背景,后者称为星状伪迹。
产生星状伪迹的原因在于:反投影的本质是把取自有限物体空间的投影均匀地回抹(反投影)到射线所及的无限空间的各点上,包括原先像素值为零的点。
(1)(2)(3)二、 反投影重建算法的数学描述我们把“取投影” 、“反投影重建” 、“重建后图像”这些环节看作是一个以原像为输入,重建后图像为输出的成像系统,如图所示,先来求该系统的点扩展函数PSF 。
图中,(,)x y 为固定坐标,(,)r r x y 为旋转坐标,(,)r θ为极坐标,设位于坐标原点0,0x y ==的点源(,)x y δ为x y -断面中唯一的像点,扫描方式为平移加旋转。
即射线先平行移动,从物体的一侧移向另一侧;然后旋转一个角度φ∆,如此继续,直到累计的旋转角达到180φ-∆。
为止。
为了计及这一几何要求我们设置一旋转坐标系统r r x y -,它绕原点转动使投影总是沿着r y 方向,r rx y -的原点与x y -的原点相同。
二者的夹角为φ,不同的φ代表不同的投射方向。
投影线的位置可由(,)r x φ完全确定。
设φ为离散取值,如i φφ=,则相应的投影为:()(,)(,)(,)()()()|(cos())i i r r i r r r r r r rr r r r i p x p x f x y dy x y dy x y dy x r φφφφδδδδδθφ+∞+∞-∞-∞+∞=-∞======-⎰⎰⎰其中cos()r x r θφ=-,这可以从图的几何关系很容易得出。
若n φφ=,则相应的投影为:cos n n p r φδθφ=-[()]根据反投影重建的定义式,点(,)r r x y 的图像在所述坐标系统中表示为:[][]cos()11111(,)(,)()|cos()1cos()i r i iiN N r r r x r ii i N ii f r f x y p x p x r N N p r φφφφθφφφφφθθφθφφπ=-======-=-∆∑∑∑其中,N φ为投影数,/N φφπ∆=。
若在有限区间内将射线增至不相重的无限条,即连续取投影,则有:[]01(,)cos()f r p r d πφθθφφπ=-⎰在忽略射束硬化的情况下,φ在(,2)ππ区间内的投影值等于(0,)π区间内的投影值。
在输入图像为点源的情况下,由及可得:(,x y δ(,)h x y 重建后图像原像图 “反投影重建”成像系统图平移加旋转扫描方式所用坐标系[]01(,)cos()h r r d πθδθφφπ=-⎰因为,[]00()()'()a a δφφδφφ-=(此公式推导可参见附录一),其中,0φ是()0a φ=的唯一的根。
令()cos()a r φθφ=-,则有:00()cos()0a r φθφ=-=因为0r ≠,所以0sin()1θφ-=,于是有:[]0000()11(,)cos()sin()1111sin()h r r d d r r r ππδφφθδθφφφππθφπθφπ-=-=-===-⎰⎰可见,相应于反投影重建算法的系统,它的点扩展函数不是δ函数,系统不是完美的。
虽然在0r =处能反映原图是点源的情况,但在0r ≠处,像素值0≠,上式定量地描述了反投影重建算法星状伪迹的本质。
若原像为(,)x y μ,则将原像取投影后再按反投影算法得到的重建图像为:(,)(,)(,)f x y x y h x y μ=**,其中**表示二维卷积。
要去除反投影算法的星状伪迹,可以在输出端加一滤波器,使加了滤波器后的反投影重建等效成像系统的点扩展函数(PSF)为(,)x y δ。
设滤波器的PSF 为(,)q x y ,相应的传递函数为[]2(,)(,)Q F q x y ξη=,要求(式的推导可参见附录一):(,)1ξη=或:(,)Q ξηπρ=这是一个二维滤波器,实现起来较麻烦。
若ρ的变化范围扩至∞,则根本不能实现。
但它提供了去除星状伪迹的一个方向。
(,)(,)q x y x y δ=三、 滤波反投影重建算法反投影重建算法的缺点是引入星状伪迹,即原来图像中密度为零的点,重建后不一定为零,从而使图像失真。
去除伪迹的方法如图所示。
(a)(b)(a)方案之一,先“反投影”再二维滤波;(b) 方案之二,先对投影数据作一维滤波,再“反 投影”图 星状伪迹的去除投影定理投影定理(或中心切片定理):在非衍射源情况下,某图像(,)f x y 在视角为φ时投影()r p x φ的一维傅氏变换给出(,)f x y 的二维傅氏变换^12(,)(,)A A ωωρφ=的一个切片。
切片与1ω轴相交成φ角,且通过坐标原点。
即:^1()(,)|r F p x A φφρφ⎡⎤=⎣⎦固定 图阐明投影定理 证明:()f x,y 的二维傅立叶变换为12()12,)()-j x y A(f x,y e dxdy ωωωω+∞+∞+-∞-∞=⎰⎰由图可以得到如下几何关系cos sin sin cos r r x x y y φφφφ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦输出图像输出图像1p φ以r y 为投影轴的投影为:()()()r r r r r r p x f x,y dy f x ,y dy φ+∞+∞-∞-∞==⎰⎰它的一维傅里叶变换为:1(cos sin )[()]()()()r r -j2x r r r-j2x r r r r r -j2x y F p x p x e dx f x ,y e dx dy f x,y e dxdyπρφφπρπρφφ+∞-∞+∞+∞-∞-∞+∞+∞+-∞-∞===⎰⎰⎰⎰⎰式中采用2πρ可以使后续反变换计算中的系数得以简化。
在推导上式的过程中,我们利用了下列关系:()()r r r f x,y f x ,y =以及cos sin sin cos r rr r r r x x xy dx dy dxdy dxdy y y xyφφφφ∂∂∂∂===∂∂-∂∂ 由式可知,当12,ωω的取值满足条件122cos 2sin ωπρφωπρφ=⎫⎬=⎭时,有121212()1cos sin 12cos sin [()]()|(,)|-j x y r 2222F p x f x,y e dxdy A ωωφωπρφωπρφωπρφωπρφωω∞∞+=-∞-∞=====⎰⎰上式说明:12,ωω不是独立的而是受到式的约束,其值必须局限于直线21(tg )ωφω=上。
根据投影定理,投影图像重建问题原则上可按如下流程求解: (1)采集不同视角下的投影;(2)求出各投影的一维傅氏变换,此即图像二维傅氏变换过原点的各切片,理论上是连续的无穷多片;(3)将上述各切片汇集成图像的二维傅氏变换; (4)求二维傅氏反变换的重建图像。
卷积反投影重建(即滤波反投影)待重建图像为),(y x a ,它的二维傅氏变换为^12(,)(,)A A ωωρφ=。
根据中心切片定理,^(,)A ρφ可通过),(y x a 在不同视角φ下的投影()r p x φ的一维傅氏变换求得。
即:待建图像:^121(,)(,)()()(,)r A A F p x PP φφωωρφρρφ⎡⎤====⎣⎦12^1212()12122^2cos()02cos()02cos()0(,)(,)(,)1(,)4(,)(,)(,)i x y i r i r i r a r a x y F A A e d d A e d d P e d d d P e d ωωππρθφππρθφππρθφθωωωωωωπρφρρφρφρρφφρρφρ-∞∞+-∞-∞∞--∞∞--∞∞--∞======⎰⎰⎰⎰⎰⎰⎰⎰[]因为cos()r x r θφ=-,所以有:122(cos sin )22cos()r x y x y x r ωωπρφφπρπρθφ+=+==-同时:12d d J d d ωωρφ=11222//2cos 2sin 4//2sin 2cos J ωρωφπφπρφπρωρωφπφπρφ∂∂∂∂-===∂∂∂∂先来看该式的第二个积分:[]22cos()cos()cos()cos()(,)(,)|()(,)|(,)|cos(),rrr r i x i r x r r r x r r x r P e d P e d h x p x g x g r πρπρθφθφθφθφρρφρρρφρφφθφφ∞∞-=--∞-∞=-=-==*==-⎰⎰式中:(,)()(,)r r r g x h x p x φφ=*式的物理意义是投影(,)r p x φ经过传递函数为1[()]r F h x ρ=的滤波器后得到的修正后的投影(,)r g x φ在满足cos()r x r θφ=-时的值。