生物统计学之方差分析
- 格式:pptx
- 大小:1.35 MB
- 文档页数:80

研究生《生物统计学》课程第五讲方差分析主要内容:一、单因素方差分析二、两因素方差分析三、多因素方差分析一、单因素方差分析[Analyze]=>[Compare Means]=>[ One-Way ANOV A](1)建立数据文件,在Variable Vew中定义变量“饲料”、“增重”,“饲料”小数位数为0,用1、2、3、4分别代表甲、乙、丙、丁4种饲料。
输入数据。
(2)方差分析:[Analyze]=>[Compare Means]=>[ One-Way ANOVA],打开[One-Way ANOVA]主对话框。
选定“增重”使之进入[Dependent List](样本观测值)框,选定“饲料”使之进入[Factor](因素)框(3)单击[Options]进入“选项”对话框,选择[Descriptive]要求输出描述统计量,[Homogeneity of Variance tese](方差齐性检验),[Continue]返回;(4)单击[Post Hoc]打开[One-Way ANOV A: Post Hoc Multiple Comparisions](单因素方差分析:验后多重比较)对话框,可选择确定多重比较方法,如LSD法、Duncan 法,[Continue]返回;(5)单击[OK],运行单因素方差分析。
结果显示:方差分析表:(P=0.005<0.01 不同饲料对鱼增重的作用差异极显著)多重比较:LSD法(解释:甲与其他三种饲料都具有显著差异,乙、丙、丁间差异不显著)Duncan法(解释:用Duncan法划分的相似性子集,在显著性水平为0.05的情况下,第一组包括丙乙丁,组内相似的概率为0.123;第二组包括甲,说明甲的均值与其他三个具有显著性差异)2、练习:某灯泡厂用四种配料方案制成的灯丝生产了四批灯泡,在每批灯泡中作随机抽样,测量其使用寿命(单位:小时),数据如下:问不同灯丝制成的灯泡的使用寿命是否有显著差异,存在差异则做多重比较。




第六章 方差分析一、方差分析的统计意义上章讨论的t 测验、u 测验是适应于两样本相比较的假设测验,不适于多样本比较,因为: 1) 对多个样本进行两两比较的t 测验手续实为麻烦。
如k =3个样本,要作3次测验;k =10个样本,作k (k -1)/2=45次测验。
2) 犯α错误的可能性增大。
因为两两之间取α=0.05,实际k 个样本,则k (k -1)/2次的α>0.05;且k 越大,α被扩大得越多。
3) 估计试验误差时的精确度有所损失。
设k 个样本,每一样本容量均为n ,则用t 测验,每次自由度v =(n -1)+(n -1)=2(n -1);对多个样本,v ’=k (n -1);当k =2时,v =v ’;当k ≥3时,v ’>v 。
又因为:12()x x s -=21212e ss ss s v v +=+ v =v 1+v 2 v 减小,s e 变大,12()x x s -变大。
二、自由度和平方和的分解设:k 组样本,每样本均具有n 个观察值(即样本容量相同),共有nk 个观察值。
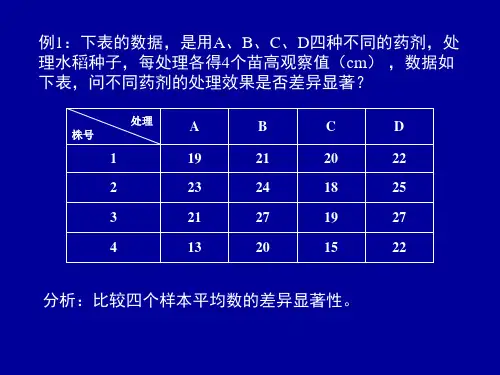
i =1~k ,j =1~nT =ij x x =∑∑T :total 总的;t :treatment ,处理;e: error, 误差 总变异:总自由度V T =kn -1总平方和SS T =2222()()ij x x x x x C nk-=-=-∑∑∑∑矫正数:C =2()x nk∑总变异可分解为组内(随机误差)和组间(效应)两部分: 组间变异:组间自由度V t =k -1组间平方和SS t =22()ii T n x x C n-=-∑∑组内变异=总变异-组间变异组内变异:V e =V T -V t =(nk -1)-(k -1)=k (n -1)【或者这样理解:每组组内自由度为(n -1),有k 组,共计:V e =k (n -1)】 组内平方和:SS e =SS T -SS t 证明从略! 均方=平方和/自由度 总均方S T 2=2()1ijxx nk --∑组间均方22()1i t n x x S k -=-∑组内均方22()(1)ix x Se k n -=-∑∑例:以A 、B 、C 、D 4种药剂处理水稻种子,其中A 为对照,每处理各得4个苗高观察值(cm ),请分解其自由度和平方和。





生物统计学中的方差分析方法生物统计学在生物学研究中起着重要的作用。
方差分析是生物统计学中使用最广泛的一种数据分析方法。
在生物学中,我们通常需要对实验数据进行统计分析,以了解变量之间的差异,并在数据集中找到潜在的关联。
方差分析可以有效地达到这一目的,它使得我们可以同时比较几组数据,以确定它们之间是否存在显著差异。
什么是方差分析?方差分析是一种统计分析方法,用于比较两个或多个组之间的平均差异。
这种分析方法可以帮助我们确定这些组之间差异的来源,例如是否由于随机误差引起,还是由于实验操作的差异引起。
方差分析的中心思想是将数据集中的差异分解为两个部分:一部分是由于组间的差异引起的,另一部分是由于组内变异引起的。
方差分析的类型在生物统计学中,有多种类型的方差分析方法,它们旨在比较不同组之间的差异。
以下是其中一些常见的方差分析类型:一元方差分析:这种方法比较一个因子对一个变量的影响。
例如,你想了解若干种不同品牌的肥料对一个植物的生长是否有影响。
双因子方差分析:这种方法比较两种因素(如肥料类型和土壤类型)对一个变量的影响。
例如,你想了解在哪种类型的土壤上,哪种品牌的肥料能够促进植物生长最好。
方差分析步骤方差分析通常需要遵循一系列严格的步骤:1. 明确假设:方差分析的第一步是明确假设。
你需要确定要研究的因素和变量,并制定假设。
例如,在上述例子中,你的假设可以是一个品牌或肥料类型比其他品牌或肥料类型更容易促进植物生长。
2. 收集数据:随后你需要收集数据,并将其整理成表格或清单。
在数据收集过程中,你需要注意样本的大小和样本的分布。
你还需要确保数据的准确性和可靠性。
3. 计算方差:接下来,你需要计算总体方差、组内方差和组间方差。
4. 计算F值:你需要使用计算得到的方差值来计算F值。
F值是组间差异和组内差异之比。
5. 确定显著性:最后,你需要确定计算得到的F值是否达到统计显著性。
优点和限制方差分析是一种灵活的分析方法,能够比较多组数据,并确定两个或多个组之间的差异。