2017北京中考数学一模圆专题

2017年北京中考数学一模28题“几何综合题”西城28．在△ABC 中，AB =BC ，BD ⊥AC 于点D ．（1）如图1，当∠ABC =90°时，若CE 平分∠ACB ，交AB 于点E ，交BD 于点F .①求证：△BEF 是等腰三角形； ②求证：()BF BC BD +=21； （2）点E 在AB 边上，连接CE . 若()BF BC BD +=21，在图2.中补全图形，判断∠ACE 与∠ABC 之间的数量关系，写出你的结论，并写出求解∠ACE 与∠ABC 关系的思路图1 图2朝阳28.在△ABC 中，∠ACB =90°，AC ＜BC ，点D 在AC 的延长线上，点E 在BC 边上，且BE =AD ， (1) 如图1，连接AE ，DE ，当∠AEB =110°时，求∠DAE 的度数；(2) 在图2中，点D 是AC 延长线上的一个动点，点E 在BC 边上（不与点C 重合），且BE =AD ，连接AE ，DE ，将线段AE 绕点E 顺时针旋转90°得到线段EF ，连接BF ,DE . ①依题意补全图形； ②求证：BF =DE .FEBDAC D A CB图1图2东城28. 在等腰△ABC中，（1）如图1，若△ABC为等边三角形，D为线段BC中点，线段AD关于直线AB的对称线段为线段AE，连接DE，则∠BDE的度数为___________；（2）若△ABC为等边三角形，点D为线段BC上一动点（不与B，C重合），连接AD并将线段AD绕点D逆时针旋转60°得到线段DE，连接BE.①根据题意在图2中补全图形；②小玉通过观察、验证，提出猜测：在点D运动的过程中，恒有CD=BE.经过与同学们的充分讨论，形成了几种证明的思路：思路1：要证明CD=BE，只需要连接AE，并证明△ADC≌△AEB；思路2：要证明CD=BE，只需要过点D作DF∥AB，交AC于F，证明△ADF≌△DEB；思路3：要证明CD=BE，只需要延长CB至点G，使得BG=CD，证明△ADC≌△DEG；……请参考以上思路，帮助小玉证明CD=BE.（只需要用一种方法证明即可）（3）小玉的发现启发了小明：如图3，若AB=AC=kBC，AD=kDE，且∠ADE=∠C，此时小明发现BE，BD，AC三者之间满足一定的的数量关系，这个数量关系是______________________.（直接给出结论无须证明）图1 图2 图3ABDC图1图2房山28. 在△ABC 中，AB=BC ，∠B=90°，点D 为直线BC 上一个动点（不与B 、C 重合），连结AD ，将线段AD 绕点D 按顺时针方向旋转90°，使点A 旋转到点E ，连结EC . （1）如果点D 在线段BC 上运动，如图1： ①依题意补全图1； ②求证：∠BAD=∠EDC③通过观察、实验，小明得出结论：在点D运动的过程中，总有∠DCE=135°.小明与同学讨论后，形成了证明这个结论的几种想法：想法一：在AB 上取一点F ，使得BF=BD ，要证∠DCE =135°，只需证△ADF ≌△DEC . 想法二：以点D 为圆心，DC 为半径画弧交AC 于点F. 要证∠DCE=135°，只需证△AFD ≌△ECD .想法三：过点E 作BC 所在直线的垂线段EF ，要证∠DCE=135°，只需证EF=CF . ……请你参考上面的想法，证明∠DCE=135°.（2）如果点D 在线段CB 的延长线上运动，利用图2画图分析，∠DCE 的度数还是确定的值吗？如果是，直接写出∠DCE 的度数；如果不是，说明你的理由.顺义28．在正方形ABCD 和正方形DEFG 中，顶点B 、D 、F 在同一直线上，H 是BF 的中点．（1）如图1，若AB =1，DG =2，求BH 的长； （2）如图2，连接AH ，GH ．图2图1BB小宇观察图2，提出猜想：AH =GH ，AH ⊥GH ．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：延长AH 交EF 于点M ，连接AG ，GM ，要证明结论成立只需证△GAM 是等腰直角三角形； 想法2：连接AC ，GE 分别交BF 于点M ，N ，要证明结论成立只需证△AMH ≌△HNG . ……请你参考上面的想法，帮助小宇证明AH =GH ，AH ⊥GH ．（一种方法即可）平谷28．在△ABC中，AB=AC，∠A=60°，点D是BC边的中点，作射线DE，与边AB交于点E，射线DE 绕点D顺时针旋转120°，与直线AC交于点F．（1）依题意将图1补全；（2）小华通过观察、实验提出猜想：在点E运动的过程中，始终有DE=DF．小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：由点D是BC边的中点，通过构造一边的平行线，利用全等三角形，可证DE=DF；想法2：利用等边三角形的对称性，作点E关于线段AD的对称点P，由∠BAC与∠EDF互补，可得∠AED 与∠AFD互补，由等角对等边，可证DE=DF；想法3：由等腰三角形三线合一，可得AD是∠BAC的角平分线，由角平分线定理，构造点D到AB，AC 的高，利用全等三角形，可证DE=DF…….请你参考上面的想法，帮助小华证明DE=DF（选一种方法即可）；（3）在点E运动的过程中，直接写出BE，CF，AB之间的数量关系．图1 备用图门头沟28. 已知△ABC ，AB AC =, BAC α∠=,在BA 的延长线上任取一点D ,过点D 作BC 的平行线交CA 的延长线于点E .（1）当60BAC ∠=︒时，如图28-1，依题意补全图形，直接写出EC ,BC ,ED 的数量关系； （2）当90BAC ∠=︒时，如图28-2，判断EC ,BC ,ED 之间的数量关系，并加以证明； （3）当BAC α∠=时（0180α︒︒＜＜），请写出EC ,BC ,ED 之间的数量关系并写出解题思路.海淀28．在ABCD 中，点B 关于AD 的对称点为B '，连接AB '，CB '，CB '交AD 于F 点.（1）如图1，90ABC ∠=︒，求证：F 为CB '的中点；（2）小宇通过观察、实验、提出猜想：如图2，在点B 绕点A 旋转的过程中，点F 始终为CB '的中点．小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：过点B '作B G '∥CD 交AD 于G 点，只需证三角形全等；想法2：连接BB '交AD 于H 点，只需证H 为BB '的中点； 想法3：连接BB '，BF ，只需证90B BC '∠=︒． ……请你参考上面的想法，证明F 为CB '的中点．（一种方法即可） （3）如图3，当135ABC ∠=︒时，AB '，CD 的延长线相交于点E ，求CE AF的值．图1图2图3B 28-1 B 28-2丰台28．在边长为5的正方形ABCD 中，点E ，F 分别是BC ，DC 边上的两个动点（不与 点B ，C ，D 重合），且AE ⊥EF ．（1）如图1，当BE = 2时，求FC 的长；（2）延长EF 交正方形ABCD 外角平分线CP 于点P ．①依题意将图2补全；②小京通过观察、实验提出猜想：在点E 运动的过程中，始终有AE =PE ．小京把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的三种想法：想法1：在AB 上截取AG =EC ，连接EG ，要证AE =PE ，需证△AGE ≌△ECP ． 想法2：作点A 关于BC 的对称点H ，连接BH ，CH ，EH ．要证AE =PE ， 需证△EHP 为等腰三角形．想法3：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM ， 要证AE =PE ，需证四边形MCPE 为平行四边形． 请你参考上面的想法，帮助小京证明AE =PE ．（一种方法即可）FABCDEF ABCDE图1 图2石景山28．在正方形ABCD 中，点E 是对角线AC 上的动点（与点A ，C 不重合），连接BE ． （1）将射线BE 绕点B 顺时针旋转45°，交直线AC 于点F .①依题意补全图1；②小研通过观察、实验，发现线段AE ，FC ，EF 存在以下数量关系： AE 与FC 的平方和等于EF 的平方．小研把这个猜想与同学们进行交流，通 过讨论，形成证明该猜想的几种想法：想法1： 将线段BF 绕点B 逆时针旋转90°，得到线段BM ， 要证AE ， FC ， EF 的关系，只需证AE ，AM ，EM 的关系.想法2：将ABE △沿BE 翻折，得到NBE △，要证AE ，FC ，EF 的关系，只需证EN ，FN ，EF 的关系.……请你参考上面的想法，用等式表示线段AE ，FC ，EF 的数量关系并证明； （一种方法即可）（2）如图2，若将直线．．BE 绕点B 顺时针旋转135°，交直线．．AC 于点F .小研完成作 图后，发现直线AC 上存在三条线段（不添加辅助线）满足：其中两条线段的平 方和等于第三条线段的平方，请直接用等式表示这三条线段的数量关系.CCB CB 通州28．在等边三角形ABC 中，E 为直线AB 上一点，连接EC .ED 与直线BC 交于点D ，ED =EC . （1）如图1，AB =1，点E 是AB 的中点，求BD 的长；（2）点E 是AB 边上任意一点（不与AB 边的中点和端点重合），依题意，将图2补全，判断AE 与BD 间的数量关系并证明；（3）点E 不在线段AB 上，请在图3中画出符合条件的一个图形.图1 图2 图3怀柔28．（1）如图1，在△ACB 和△ADB 中，∠C=∠D =90°，过A ，B ，C 三点可以作一个圆，此时AB 为圆的直径，AB 的中点O 为圆心.因为∠D =90°，利用圆的定义可知点D 也在此圆上，若连接DC ，当∠CAB=31°时，利用圆的知识可知∠CDB= 度.（2）如图2，在△ACB 中，∠ACB=90°，AC=BC=3，CE ⊥AB 于E ，点F 是CE 中点，连接AF 并延长交BC于点D.CG ⊥AD 于点G ，连接EG. ①求证:BD=2DC;②借助（1）中求角的方法，写出求EG 长的思路.（可以不写出计算的结果）图2 G FE DC B A 图1OB A西城28．证明：在△ABC 中，AB =BC ，BD ⊥AC 于点D . ∴∠ABD =∠CBD ，AD =BD ．(1) ①∵∠ABC =90°， ∴∠ACB =45°. ∵CE 平分∠ACB ∴∠ECB =∠ACE =22.5°.∴∠BEF =∠CFD =∠BFE =67.5°. ∴BE =BF .∴△BEF 是等腰三角形. ······························································· 2分②延长AB 至M ，使得BM =AB ，连接CM. ∴BD ∥CM ，BD =21CM ∴∠BCM =∠DBC =∠ABD =∠BMC =45°， ∠BFE =∠MCE . ∴BC =BM.由①可得，∠BEF =∠BFE ，BE =BF .∴∠BFE =∠MCE =∠BEF . ∴EM =MC ∴()BF BC BD +=21 ···········································分(2)∠ACE =41∠ABCa.与（1）②同理可证BD ∥PC ，BD =21PC ，BP =BC ； b.由()12BD BC BE =+可知△PEC 和△BEF 分别是等腰三角形； c.由∠BEF +∠BFE +∠EBF =180°，∠FCD +∠DFC =90°，可知∠ACE =41∠ABC············································································································ 7分东城28.解：,60. ..AD DE ADE ADE ABC EAB DAC AB AC AE AD EAB DAC CD BE =∠=︒∴∴∠=∠==∴∴=，△为等边三角形.△为等边三角形,，，△≌△EE（1）30°； …………1分 （2）思路1：如图，连接AE .…………5分思路2：过点D 作DF ∥AB ，交AC 于F .…………5分思路3：延长CB 至G ，使BG =CD.…………5分（3）k (BE +BD )=AC . …………7分=60.,=60..===60,.,..ABC AC BC BAC DF AB DFC CDF AF BD ADE ACB ABC DAF EDB AD DE ADF DEB DF BE CD ∴=∠︒∴∠︒∴∴=∠∠∠︒∴∠=∠=∴∴==△为等边三角形，，∥△为等边三角形.又△≌△=60.,.===60,.,.,==60..ABC AC BC BAC CD BG DG AC ADE ACB ABC DAF EDB AD DE ADC DEG CD EG BG C G BGE BE BG CD ∴=∠︒=∴=∠∠∠︒∴∠=∠=∴∴==∠∠︒∴∴==△为等边三角形,，又△≌△△为等边三角形.EABDC朝阳28．（1）解：∵ÐAEB =110°,ÐACB =90°,∴ÐDAE =20°.（2）①补全图形，如图所示.②证明：由题意可知∠AEF =90°，EF =AE .∵∠ACB =90°，∴∠AEC +∠BEF =∠AEC +∠DAE =90°. ∴∠BEF =∠DAE . ∵BE =AD ， ∴△EBF ≌△ADE ．∴DE =BF ．房山28.（1）补全图形 ------1分 （2）证明：∵∠B =90º∴∠BAD+∠BDA =90º∵∠ADE =90º，点D 在线段BC 上 ∴∠BAD+∠EDC =90º∴∠BAD=∠EDC ------2分 证法1：在AB 上取点F ，使得BF=BD ，连结DF ------3分 ∵BF =BD ，∠B =90º ∴∠BFD =45º∴∠AFD =135º∵BA=BC∴AF=CD ------4分 在△ADF 和△DEC 中⎪⎩⎪⎨⎧=∠=∠=DE AD CDE BAD CDAF ∴△ADF ≌△DEC ------5分 ∴∠DCE =∠AFD =135º ------6分证法2：以D 为圆心，DC 为半径作弧交AC 于点F ，连结DF ------3分 ∴DC=DF ∠DFC =∠DCF ∵AB=BC ∠B =90º∴∠ACB =45º ∠DFC =45º∴∠FDC =90º ∠AFD =135º ∵∠ADE =∠FDC =90º∴∠ADF =∠EDC ------4分 又∵AD =DE DF =DC∴△ADF ≌△CDE ------5分 ∴∠AFD =∠DCE =135º ------6分EFA B D C证法3：过点E 作EF ⊥BC 交BC 延长线于点F ------3分 ∴∠EFD =90º∵∠B =90º， ∴∠EFD =∠B∵∠BAD =∠CDE ，AD=DE∴△ABD ≌△DEF ------4分 ∴AB=DF BD=EF∵AB=BC∴BC=DF ，BC -DC =DF -DC 即BD =CF ------5分 ∴EF =CF ∵∠EFC =90º∴∠ECF =45º，∠DCE =135º ------6分 （2）∠DCE =45º ------7分顺义28．（1）解：∵ 正方形中ABCD 和正方形DEFG ，∴ △ABD ，△GDF 为等腰直角三角形．∵ AB =1，DG =2，∴ 由勾股定理求得BD=2，DF=22．…………………………… 2分 ∵ B 、D 、F 共线， ∴ BF =23． ∵ H 是BF 的中点， ∴ BH =21BF =223． …………………………………………………… 3分 5（2）证法一：延长AH 交EF 于点M ，连接AG ，GM ，∵正方形中ABCD 和正方形DEFG 且B 、D 、F 共线，∴AB ∥EF ．∴∠ABH=∠MFH ．又∵BH=FH ,∠AHB =∠MHF ，∴△ABH ≌△MFH ．…………… 4分 ∴AH=MH ，AB=MF ． ∵AB=AD ， ∴AD=MF ．∵DG=FG ，∠ADG=∠MFG =90°， ∴△ADG ≌△MFG ．…………… 5分 ∴∠AGD=∠MGF ，AG=MG ． 又∵∠DGM +∠MGF=90°， ∴∠AGD +∠DGM=90°．∴△AGM 为等腰直角三角形．…………………………………… 6分 ∵AH=MH ，∴AH =GH ，AH ⊥GH ．…………………………………………… 7分证法二：连接AC ，GE 分别交BF 于点M ，N ，∵正方形中ABCD 和正方形DEFG 且B 、D 、F 共线，∴AC ⊥BF ，GE ⊥BF ，DM =21BD ，DN=21DF ． ∴∠AMD =∠GNH =90°，MN =21BF ．………………………… 4分∵H 是BF 的中点， ∴BH =21BF ． ∴BH=MN ．∴BH -MH=MN -MH ． ∴BM=HN ．∵AM=BM=DM ， ∴AM=HN=DM ．∴MD+DH=NH+DH ． ∴MH=DN ． ∵DN = GN ， ∴MH = GN ．∴△AMH ≌△HNG ． ……………………………………………… 5分 ∴AH=GH ，∠AHM=∠HGN ． …………………………………… 6分 ∵∠HGN +∠GHN=90°， ∴∠AHM +∠GHN=90°． ∴∠AHG=90°．∴AH ⊥GH ． ………………………………………………………… 7分平谷28．解：（1）如图1， (1)（2）想法1证明：如图2，过D 作DG ∥AB ，交AC 于G ， (2)图2 GF DCABE 图3P F DCAB E图4N M F DCABE 图1F DCABE∵点D是BC边的中点，∴DG=12 AB．∴△CDG是等边三角形．∴∠EDB+∠EDG=120°．∵∠FDG+∠EDG=120°，∴∠EDB =∠FDG． (3)∵BD=DG，∠B=∠FGD=60°，∴△BDE≌△GDF． (4)∴DE=DF． (5)想法2证明：如图3，连接AD，∵点D是BC边的中点，∴AD是△ABC的对称轴．作点E关于线段AD的对称点P，点P在边AC上， (2)∴△ADE≌△ADP．∴DE=DP，∠AED=∠APD．∵∠BAC+∠EDF=180°，∴∠AED+∠AFD=180°．∵∠APD+∠DPF=180°，∴∠AFD=∠DPF． (3)∴DP=DF． (4)∴DE=DF． (5)想法3证明：如图4，连接AD，过D作DM⊥AB于M，DN⊥AB于N， (2)∵点D是BC边的中点，∴AD平分∠BAC．∵DM⊥AB于M，DN⊥AB于N，∴DM=DN． (3)∵∠A=60°，∴∠MDE+∠EDN=120°．∵∠FDN+∠EDN=120°，∴∠MDE=∠FDN．∴Rt△MDE≌Rt△NDF． (4)∴DE=DF． (5)（3）当点F在AC边上时，12BE CF AB+=； (6)当点F在AC延长线上时，12BE CF AB-=． (7)门头沟28.（1）补全图形正确 . …………………1分数量关系：EC=BC + ED. …………2分（2）数量关系：BC ED+=.过D作DF∥AC交BC延长线于F点F∵DF ∥AC ，ED ∥BC ，∴四边形ADCF 为平行四边形. ∴ED=CF , EC=DF . ∵AB =AC ， ∴∠ABC =∠ACB . ∵ED ∥BC ，∴∠DEC =∠ECB , ∠EDB =∠DBC . ∴∠CED =∠BDE . ∴AE =AD .∴EC =BD . …………………3分 ∴BD =DF . ∵DF ∥AC ，∴∠BDF =∠BAC =90°.∴△BDF 为等腰直角三角形.…………………4分 在Rt △BDF 中 ∵BF 2=BD 2+DF 2，∴(BC +ED)2=2EC 2.BC ED += . …………………5分（3）数量关系：2sin2BC ED EC α+=⋅.……6分①由（2）可知四边形ACFD 为平行四边形，△BDF 为等腰三角形 过D 点作DN ⊥BC 于N 点可得BN =12BF ，∠BDN =12α②在Rt △BDN 中 Sin ∠BDN =BN BD =sin 2α. 可得2sin 2BC ED EC α+=⋅.……………………………7分海淀28．（1）证明：∵四边形ABCD 为平行四边形，∠ABC =90°， ∴□ABCD 为矩形，AB=CD .∴. ∠D =∠BAD = 90°.∵ B ，B '关于AD 对称，∴ ∠B 'AD =∠BAD =90°，AB =A B '．----------------- 1分 ∴ ∠B 'AD =∠D ． ∵ ∠AF B '=∠CFD ，∴ △AF B '≌ △CFD （AAS ）. ∴ F B '=FC ．∴ F 是C B '的中点． ---------------------------------------------------------------------------- 2分 （2）证明：方法1：过点B '作B G '∥CD 交AD 于点G ． ∵ B ，B '关于AD 对称， ∴ ∠1=∠2，AB =A B '． ∵ B 'G ∥CD ， AB ∥CD ， ∴ B 'G ∥AB ． ∴ ∠2=∠3． ∴ ∠1=∠3． ∴ B 'A =B 'G ． ∵ AB =CD ，AB =A B '，∴ B 'G =CD ． ------------------------------------------------------------------------------------- 3分 ∵ B 'G ∥CD ，∴ ∠4=∠D ．----------------------------------------------------------------------------------------- 4分 ∵ ∠B 'FG =∠CFD ，∴ △B 'FG ≌ △CFD （AAS ）. ∴ F B '=FC ．∴ F 是C B '的中点． ---------------------------------------------------------------------------- 5分方法2：连接BB '交直线AD 于H 点， ∵ B ，B '关于AD 对称，∴ AD 是线段B 'B 的垂直平分线．∴ B 'H =HB ．----------------------------- 3分 ∵ AD ∥BC ，∴''1B F B HFC HB ==．-------------------- 4分 ∴ F B '=FC ．∴ F 是C B '的中点． --------------------------------------------------------------------------- 5分 方法3：连接BB '，BF ，∵ B ，B '关于AD 对称， ∴ AD 是线段B 'B 的垂直平分线． ∴ B 'F =FB ．----------------------------- 3分 ∴ ∠1=∠2． ∵ AD ∥BC ， ∴ B 'B ⊥BC ． ∴ ∠B 'BC =90°．∴ ∠1+∠3=90°，∠2+∠4=90°． ∴ ∠3=∠4．∴ FB =FC ．------------------------------------------------------------------------------------------- 4分 ∴ B 'F =FB =FC ．∴ F 是C B '的中点． --------------------------------------------------------------------------- 5分 （3）解：取B 'E 的中点G ，连结GF . ∵ 由（2）得，F 为C B '的中点，∴ FG ∥CE ，12FG CE =．…① ∵ ∠ABC =135°，□ABCD 中，AD ∥BC ，∴ ∠BAD =180°-∠ABC =45°． ∴ 由对称性，∠EAD =∠BAD =45°. ∵ FG ∥CE ，AB ∥CD ， ∴ FG ∥AB ．∴ ∠GF A =∠F AB =45°. ----------------------------------------------------------------------------- 6分 ∴ ∠FGA =90°，GA =GF ． ∴sin FG EAD AF =∠⋅=．…② ∴由①，②可得CEAF------------------------------------------------------------------ 7分丰台28. 解：（1）∵正方形ABCD 的边长为5， BE =2， ∴EC =3.∵四边形ABCD 是正方形， ∴∠B =∠C= 90°， ∴∠1+∠3=90°，∵AE ⊥EF ，∴∠2+∠3=90°， ∴∠1=∠2. ∴△ABE ∽△ECF ，∴FC CE BE AB =，即FC325= ∴FC =56. ………………………………………………………………………2分（2）①依题意补全图形. ……………………………………………………………3分②法1：证明：在AB 上截取AG =EC ，连接EG . ∵AB = BC ，∴GB =EB .∵∠B =90°，∴∠BGE =45°，∴∠AGE =135°. ∵∠DCB =90°，CP 是正方形ABCD 外角平分线， ∴∠ECP =135°. ∴∠AGE =∠ECP .BCE DA F P G 12 F A DC BE132又∵∠1=∠2，∴△AGE ≌△ECP .∴AE =PE . ………………………………………………………………7分法2：证明：作点A 关于BC 的对称点H ，连接BH ，CH ，EH . ∴AB =BH=BC ，∠1=∠4，∠ABE =∠HBE =90°. ∴∠BHC =∠BCH =45°，∠4+∠5=45°.∵∠1=∠2，∴∠2+∠5=45°. ∵∠ECP =135°，∴∠HCP =180°，点H ，C ，P 在同一条直线上.∵∠6=∠2+∠P =45°，∴∠5 =∠P .∴AE =PE . ………………………………………………………………7分法3：证明：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM . ∴MB =EB ，∴∠MEB =45°，∠MEC =135°. 由法1∠ECP =135°，∴∠MEC =∠ECP . ∴ME ∥PC .又∵AB =BC ，∠ABC =∠MBC =90°. ∴△ABE ≌△CBF .∴∠1=∠BCM ，MC =AE .∴MC ∥EP .∴四边形MCPE 为平行四边形. ∴MC =PE .∴AE =PE . ………………………………………………………………7分石景山28．（1）①依题意补全图形，如图1．…………………… 1分②线段AE ，FC ，EF 的数量关系为：222AE FC EF +=． ……… 2分B CE DA F PM112BCEDA F P H4 5 6 M证法一： 过点B 作MBBF 于点B 且BM BF ，连接ME ，MA ，如图2．∵四边形ABCD 是正方形， ∴901245ABC AB BC °，°，．∵345°，∴345MBE °．又∵BEBE ， ∴MBE FBE △≌△． ………………………………… 3分 ∴EM EF ．∵490ABF °，590ABF °，∴45． 又∵,BMBF ABCB ，∴AMB CFB △≌△． ………………………………… 4分 ∴AM CF ，6245°．∴6190MAE°．在Rt MAE △中，222AE MA EM +=．∴222AE FC EF +=． ………………………………… 5分 证法二： 作2=1，且BN BA ，连接EN ，FN ，如图3．又∵BEBE ，∴BNE BAE △≌△．分 ∴,NEAE 6=5．∵四边形ABCD 是正方形， ∴905845ABC AB BC °，°，．∴BN BC ．∵32452EBF°-，4190451451ABCEBF °°°，∴34．又∵BFBF ，∴BNF BCF △≌△． ………………………………… 4分 ∴FNFC ，7845°．∴67454590ENF °°°．MHABC D EFG∴在Rt ENF △中，222NE FN EF +=．∴222AE FC EF +=． ………………………………… 5分 （2）用等式表示这三条线段的数量关系：222AF EC EF +=． …………… 7分通州 28.解：（1）……………………..(1分)21=BD …………..(2分) （2）AE =BD ……..(3分)证明思路1：利用等边三角形的性质， 证明△BDE 与EC 所在的三角形全等； 证明思路2：利用等腰三角形的轴对称性， 作出△BDE 的轴对称图形；证明思路3:将△BDE 绕BE 边的中点旋转180°，构造平行四边形； ……………………..(6分) ……（3）图形正确 ……………………..(7分)怀柔28． 解：（1）31°. ……………………………2分（2）①过点E 作EH ∥AD 交CB 于H 点. ……………………3分 ∵CE ⊥AB 于点E ，AC=BC ， ∴点E 是AB 中点.∴BH=DH. ∵点F 是CE 中点，∴HD=DC.∴BD=2CD. ……………………………4分 ②∵CE ⊥AB 于点E ，∴∠CEA=90°.∵CG ⊥AD 于点G ，∴∠CGA=90°.∴AC 为圆的直径. ∵∠ACB=90°，AC=BC ，∴∠CAE =45°.∵CE ⊥AB 于点E ，∴∠ACE =45°.∴∠AGE=45°. ……………………………5分 方法1：解斜三角形法在Rt △DCA 中，因为∠C =90°, CG ⊥AD 于点G ，DC=1. 所以可以求出CG 的长. ……………………………6分 又因为∠CGE==135°,CE=2. 解△ECG 可求出EG 的长.（此题解△AEG 也可行）…………………7分 方法2：证明等腰直角三角形法.CG F E D C B A K A B C D E FG 延长CG 交EH 于M 点.因为EH ∥AD 交CB 于H 点，点F 是CE 中点，所以点G 为MC 的中点.因为==.∴CG=10.∴MG=10.……………………6分 因为∠EGA=∠ACE=45°,所以∠CGE==135°.所以∠MGE=∠GEM=45°,所以GE 可解.∵.，∴.………………………7分 方法3：相似法 ∵AC=BC=3，∴AB=∴AE=2. ∵CD=1，∴BD=2，AD =. ∵∠AGE=∠B= 45°, ∠DAB=∠EAD.∴△AGE △ABD. …………………6分 ∴AE GE AD DB =.2EG =.∴.………………………7分 方法4：旋转法：过E 作EK ⊥GE 交AD 于点K ，可证△AKE ≅△CGE （ASA ）. …………………6分 ∴.∵CD=1，AD =,∴∴KG=5.∴EG=5.……………………………7分。

几何综合题型汇总1.（2017东城一模）在等腰△ABC中，（1）如图1，若△ABC为等边三角形，D为线段BC中点，线段AD关于直线AB的对称线段为线段AE，连接DE，则∠BDE的度数为___________；（2）若△ABC为等边三角形，点D为线段BC上一动点（不与B，C重合），连接AD并将线段AD绕点D逆时针旋转60°得到线段DE，连接BE.①根据题意在图2中补全图形；②小玉通过观察、验证，提出猜测：在点D运动的过程中，恒有CD=BE.经过与同学们的充分讨论，形成了几种证明的思路：思路1：要证明CD=BE，只需要连接AE，并证明△ADC≌△AEB；思路2：要证明CD=BE，只需要过点D作DF∥AB，交AC于F，证明△ADF≌△DEB；思路3：要证明CD=BE，只需要延长CB至点G，使得BG=CD，证明△ADC≌△DEG；……请参考以上思路，帮助小玉证明CD=BE.（只需要用一种方法证明即可）（3）小玉的发现启发了小明：如图3，若AB=AC=kBC，AD=kDE，且∠ADE=∠C，此时小明发现BE，BD，AC三者之间满足一定的的数量关系，这个数量关系是______________________.（直接给出结论无须证明）图1 图2 图32．（2017西城一模）在△ABC 中，AB =BC ，BD ⊥AC 于点D ．（1）如图1，当∠ABC =90°时，若CE 平分∠ACB ，交AB 于点E ，交BD 于点F .①求证：△BEF 是等腰三角形； ②求证：()BF BC BD +=21； （2）点E 在AB 边上，连接CE . 若()BF BC BD +=21，在图2.中补全图形，判断∠ACE 与∠ABC 之间的数量关系，写出你的结论，并写出求解∠ACE 与∠ABC 关系的思路图1 图23．（2017海淀一模）在ABCD 中，点B 关于AD 的对称点为B '，连接AB '，CB '，CB '交AD 于F 点.（1）如图1，90ABC ∠=︒，求证：F 为CB '的中点；（2）小宇通过观察、实验、提出猜想：如图2，在点B 绕点A 旋转的过程中，点F 始终为CB '的中点． 小宇把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法： 想法1：过点B '作B G '∥CD 交AD 于G 点，只需证三角形全等；想法2：连接BB '交AD 于H 点，只需证H 为BB '的中点； 想法3：连接BB '，BF ，只需证90B BC '∠=︒． ……请你参考上面的想法，证明F 为CB '的中点．（一种方法即可） （3）如图3，当135ABC ∠=︒时，AB '，CD 的延长线相交于点E ，求CE AF的值．图1 图2 图34.（2017朝阳一模）在△ABC中，∠ACB=90°，AC＜BC，点D在AC的延长线上，点E在BC边上，且BE=AD，(1) 如图1，连接AE，DE，当∠AEB=110°时，求∠DAE的度数；(2) 在图2中，点D是AC延长线上的一个动点，点E在BC边上（不与点C重合），且BE=AD，连接AE，DE，将线段AE绕点E顺时针旋转90°得到线段EF，连接BF,DE.①依题意补全图形；②求证：BF=DE.图1 图25．（2017丰台一模）在边长为5的正方形ABCD 中，点E ，F 分别是BC ，DC 边上的两个动点（不与点B ，C ，D 重合）， 且AE ⊥EF ．（1）如图1，当BE = 2时，求FC 的长；（2）延长EF 交正方形ABCD 外角平分线CP 于点P ．①依题意将图2补全；②小京通过观察、实验提出猜想：在点E 运动的过程中，始终有AE =PE ．小京把这个猜想与同学们进行交流， 通过讨论，形成了证明该猜想的三种想法：想法1：在AB 上截取AG =EC ，连接EG ，要证AE =PE ，需证△AGE ≌△ECP ．想法2：作点A 关于BC 的对称点H ，连接BH ，CH ，EH ．要证AE =PE ，需证△EHP 为等腰三角形． 想法3：将线段BE 绕点B 顺时针旋转90°，得到线段BM ，连接CM ，EM ，要证AE =PE ，需证四边形MCPE 为平行四边形．请你参考上面的想法，帮助小京证明AE =PE ．（一种方法即可）FA BCD EF A BCDE图1 图26．（2017石景山一模）在正方形ABCD 中，点E 是对角线AC 上的动点（与点A ，C 不重合），连接BE ． （1）将射线BE 绕点B 顺时针旋转45°，交直线AC 于点F .①依题意补全图1；②小研通过观察、实验，发现线段AE ，FC ，EF 存在以下数量关系：AE 与FC 的平方和等于EF 的 平方．小研把这个猜想与同学们进行交流，通过讨论，形成证明该猜想的几种想法：想法1： 将线段BF 绕点B 逆时针旋转90°，得到线段BM ， 要证AE ， FC ，EF 的关系，只需证AE ，AM ，EM 的关系.想法2：将ABE △沿BE 翻折，得到NBE △，要证AE ，FC ，EF 的关系，只需证EN ，FN ，EF 的关系. ……请你参考上面的想法，用等式表示线段AE ，FC ，EF 的数量关系并证明；（一种方法即可） （2）如图2，若将直线．．BE 绕点B 顺时针旋转135°，交直线．．AC 于点F .小研完成作图后，发现直线AC 上存在三条线段（不添加辅助线）满足：其中两条线段的平方和等于第三条线段的平方，请直接用等式表示ABDC图1图27. （2017房山一模）在△ABC 中，AB=BC ，∠B=90°，点D 为直线BC 上一个动点（不与B 、C 重合），连结AD ， 将线段AD 绕点D 按顺时针方向旋转90°，使点A 旋转到点E ，连结EC . （1）如果点D 在线段BC 上运动，如图1： ①依题意补全图1； ②求证：∠BAD=∠EDC③通过观察、实验，小明得出结论：在点D运动的过程中，总有∠DCE=135°.小明与同学讨论后，形成了证明这个结论的几种想法： 想法一：在AB 上取一点F ，使得BF=BD ，要证∠DCE =135°，只需证△ADF ≌△DEC .想法二：以点D 为圆心，DC 为半径画弧交AC 于点F. 要证∠DCE=135°，只需证△AFD ≌△ECD . 想法三：过点E 作BC 所在直线的垂线段EF ，要证∠DCE=135°，只需证EF=CF .……请你参考上面的想法，证明∠DCE=135°.（2）如果点D 在线段CB 的延长线上运动，利用图2画图分析，∠DCE 的度数还是确定的值吗？ 如果是，直接写出∠DCE 的度数；如果不是，说明你的理由.CCB CB 8．（2017通州一模）在等边三角形ABC 中，E 为直线AB 上一点，连接EC .ED 与直线BC 交于点D ，ED =EC . （1）如图1，AB =1，点E 是AB 的中点，求BD 的长；（2）点E 是AB 边上任意一点（不与AB 边的中点和端点重合），依题意，将图2补全，判断AE 与BD 间的 数量关系并证明；（3）点E 不在线段AB 上，请在图3中画出符合条件的一个图形.图1 图2 图3BCBC9.（2017门头沟一模）已知△ABC ，AB AC =, BAC α∠=,在BA 的延长线上任取一点D ,过点D 作BC 的平行线 交CA 的延长线于点E .（1）当60BAC ∠=︒时，如图1，依题意补全图形，直接写出EC ,BC ,ED 的数量关系； （2）当90BAC ∠=︒时，如图2，判断EC ,BC ,ED 之间的数量关系，并加以证明；（3）当BAC α∠=时（0180α︒︒＜＜），请写出EC ,BC ,ED 之间的数量关系并写出解题思路.图1图2图1备用图10.（2017平谷一模）在△ABC 中，AB =AC ，∠A =60°，点D 是BC 边的中点，作射线DE ，与边AB 交于点E ，射线DE 绕点D 顺时针旋转120°，与直线AC 交于点F ．（1）依题意将图1补全；（2）小华通过观察、实验提出猜想：在点E 运动的过程中，始终有DE=DF ．小华把这个猜想与同学们进行交流， 通过讨论，形成了证明该猜想的几种想法：想法1：由点D 是BC 边的中点，通过构造一边的平行线，利用全等三角形，可证DE =DF ； 想法2：利用等边三角形的对称性，作点E 关于线段AD 的对称点P ，由∠BAC 与∠EDF 互补，可得 ∠AED 与∠AFD 互补，由等角对等边，可证DE =DF ；想法3：由等腰三角形三线合一，可得AD 是∠BAC 的角平分线，由角平分线定理，构造点D 到AB ，AC 的高， 利用全等三角形，可证DE =DF …….请你参考上面的想法，帮助小华证明DE =DF （选一种方法即可）； （3）在点E 运动的过程中，直接写出BE ，CF ，AB 之间的数量关系．图2图1FB11.（2017顺义一模）在正方形ABCD 和正方形DEFG 中，顶点B 、D 、F 在同一直线上，H 是BF 的中点．（1）如图1，若AB =1，DG =2，求（2）如图2，连接AH ，GH ．小宇观察图2，提出猜想：AH =GH ，AH ⊥GH ．小宇把这个猜想与同学们进行交流，通过讨论，形成了 证明该猜想的几种想法：想法1：延长AH 交EF 于点M ，连接AG ，GM ，要证明结论成立只需证△GAM 是等腰直角三角形； 想法2：连接AC ，GE 分别交BF 于点M ，N ，要证明结论成立只需证△AMH ≌△HNG . ……请你参考上面的想法，帮助小宇证明AH =GH ，AH ⊥GH ．（一种方法即可）图2GFDCBA图1OBA12.（2017怀柔一模）（1）如图1，在△ACB 和△ADB 中，∠C=∠D =90°，过A ，B ，C 三点可以作一个圆，此时AB为圆的直径，AB 的中点O 为圆心.因为∠D=90°，利用圆的定义可知点D 也在此圆上，若连接DC ，当∠CAB=31° 时，利用圆的知识可知∠CDB=度.（2）如图2，在△ACB 中，∠ACB=90°，AC=BC=3，CE ⊥AB 于E ，点F 是CE 中点，连接AF 并延长交BC 于点D. CG ⊥AD 于点G ，连接EG.①求证:BD=2DC;②借助（1）中求角的方法，写出求EG 长的思路.（可以不写出计算的结果）13.（2017大兴一模）已知，在Rt△ABC中，∠B=90°，AB=3，BC=3，在BC边上取两点E，F（点E在点F左侧），以EF为边作等边三角形DEF，使顶点D与E在边AC异侧，DE，DF分别交AC于点G，H，连结AD.（1）如图1，求证：DE⊥AC；（2）如图2，若∠DAC=30°，△DEF的边EF在线段BC上移动.写出DH与BE的数量关系并证明；（3）若30°<∠DAC<60°，△DEF的周长为m，则m的取值范围是.。

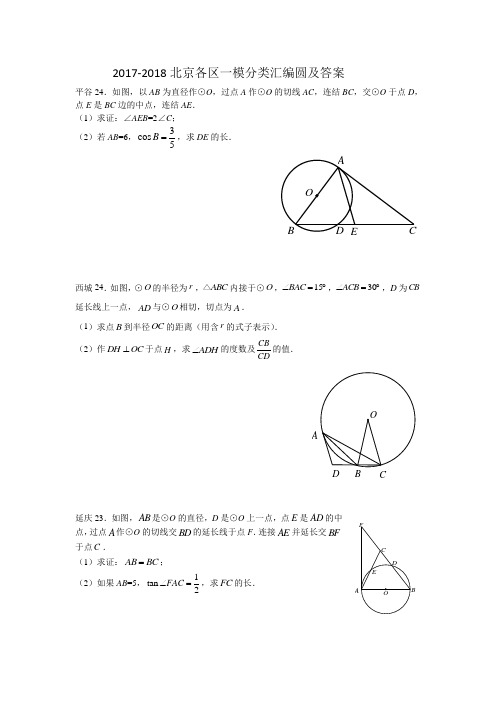
2017-2018北京各区一模分类汇编圆及答案平谷24．如图，以AB 为直径作⊙O ，过点A 作⊙O 的切线AC ，连结BC ，交⊙O 于点D ，点E 是BC 边的中点，连结AE ． （1）求证：∠AEB =2∠C ； （2）若AB =6，3cos 5B =，求DE 的长．西城24．如图，⊙O 的半径为r ，ABC △内接于⊙O ，15BAC ∠=︒，30ACB ∠=︒，D 为CB 延长线上一点，AD 与⊙O 相切，切点为A ． （1）求点B 到半径OC 的距离（用含r 的式子表示）． （2）作DH OC ⊥于点H ，求ADH ∠的度数及CBCD的值．AB C延庆23．如图，AB 是⊙O 的直径，D 是⊙O 上一点，点E 是AD 的中点，过点A 作⊙O 的切线交BD 的延长线于点F ．连接AE 并延长交BF 于点C ．（1）求证：AB BC =；（2）如果AB =5，1tan 2FAC ∠=，求FC 的长．A海淀23．如图，AB 是O 的直径，弦EF AB ⊥于点C ，过点F 作O 的切线交AB 的延长线于点D .（1）已知A α∠=，求D ∠的大小（用含α的式子表示）； （2）取BE 的中点M ，连接MF ，请补全图形；若30A ∠=︒，MF ，求O 的半径.大兴23.已知：如图，在△OAB 中，OA OB =，⊙O 经过AB 的中点C ，与OB 交于点D,且与BO 的延长线交于点E ，连接EC CD ，． （1）试判断AB 与⊙O 的位置关系，并加以证明； （2）若1tan 2E =，⊙O 的半径为3，求OA 的长．怀柔23.如图，AC 是⊙O 的直径，点B 是⊙O 内一点，且BA=BC ，连结BO 并延长线交⊙O 于点D ，过点C 作⊙O 的切线CE ，且BC 平分∠DBE. (1)求证：BE=CE ；(2)若⊙O 的直径长8，sin ∠BCE=45，求BE 的长.DA第23题图A顺义24．如图，等腰△ABC 是⊙O 的内接三角形，AB =AC ，过点A 作BC 的平行线AD 交BO 的延长线于点D ．（1）求证：AD 是⊙O 的切线；（2）若⊙O 的半径为15，sin ∠D ＝35，求AB 的长．房山22（此题无答案）．如图，AB 、BF 分别是⊙O 的直径和弦，弦CD 与AB 、BF 分别相交于点E 、G ，过点F 的切线HF 与DC 的延长线相交于点H ，且HF ＝（1）求证：AB ⊥CD ；（2）若sin ∠HGF ＝43，BF ＝3，求⊙O 的半径长.门头沟23. 如图，AB 为⊙O 直径，过⊙O 外的点D 作DE ⊥OA 于点E ，射线DC 切⊙O于点C 、交AB 的延长线于点P ，连接AC 交DE 于点F ，作CH ⊥AB 于点H ． （1）求证：∠D =2∠A ；（2）若HB =2，cos D =35，请求出AC 的长．丰台23．如图，A，B，C三点在⊙O上，直径BD平分∠ABC，过点D作DE∥AB交弦BC 于点E，过点D作⊙O的切线交BC的延长线于点F．（1）求证：EF ED；（2）如果半径为5，cos∠ABC =35，求DF的长．东城23．如图，AB为O的直径，点C，D在O上，且点C是BD的中点.过点C作AD的垂线EF交直线AD于点E.（1）求证：EF是O的切线；（2）连接BC. 若AB=5，BC=3，求线段AE的长.朝阳25．（本小题5分）如图，在△ABC中，AB=BC，∠A=45°，以AB为直径的⊙O交CO于点D．（1）求证：BC是⊙O的切线；（2）连接BD，若BD=m，tan∠CBD=n，写出求直径AB的思路．燕山25．如图，在△ABC 中,AB=AC ,AE 是BC 边上的高线，BM 平分∠ABC 交 AE 于点M ，经过 B ，M 两点的⊙O 交 BC 于点G ，交AB 于点F ，FB 为⊙O 的直径． （1）求证：AM 是⊙O 的切线 （2）当BE =3，cosC=52时，求⊙O 的半径．答案24．（1）证明：∵AC 是⊙O 的切线， ∴∠BAC =90°．..................................................................... 1 ∵点E 是BC 边的中点， ∴AE=EC ． ∴∠C =∠EAC ， ...................................................................... 2 ∵∠AEB =∠C +∠EAC ， ∴∠AEB =2∠C ． .. (3)（2）解：连结AD ．∵AB 为直径作⊙O ， ∴∠ABD =90°． ∵AB = 6，3cos 5B =， ∴BD =185． (4)在Rt △ABC 中，AB =6，3cos 5B =，∴BC =10．∵点E 是BC 边的中点， ∴BE =5． ····························· 5 ∴75DE =． ························ 6 24.（1）如图4，作BE OC ⊥于点E ． ∵在⊙O 的内接ABC △中，15BAC ∠=︒， ∴230BOC BAC ∠=∠=︒．在Rt BOE △中，90OEB ∠=︒，30BOE ∠=︒，OB r =， ∴22OB rBE ==， ∴点B 到半径OC 的距离为2r． （2）如图4，连接OA ．由BE OC ⊥，DH OC ⊥，可得BE DH ∥． ∵AD 于⊙O 相切，切点为A ， ∴AD OA ⊥， ∴90OAD ∠=︒． ∵DH OC ⊥于点H ， ∴90OHD ∠=︒．∵在OBC △中，OB OC =，30BOC ∠=︒，∴180752BOCOCB ︒-∠∠==︒．∵30ACB ∠=︒，∴45OCA OCB ACB ∠=∠-∠=︒． ∵OA OC =，∴45OAC OCE ∠=∠=︒， ∴180290AOC OCA ∠=︒-∠=︒， ∴四边形AOHD 为矩形，90ADH ∠=︒， ∴DH AO r ==．∵2r BE =， ∴2DHBE =．∵BE DH ∥， ∴CBE CDH ∽△△， ∴12CB BE CD DH ==． 图4CB A23．证明：（1）连接BE ．∵AB 是直径， ∴∠AEB =90°．∴∠CBE +∠ECB =90°∠EBA +∠EAB =90°． ∵点E 是AD 的中点， ∴∠CBE =∠EBA ．∴∠ECB =∠EAB ． ……1分 ∴AB =BC ． ……2分（2）∵FA 作⊙O 的切线， ∴FA ⊥AB ． ∴∠FAC +∠EAB =90°． ∵∠EBA +∠EAB =90°， ∴∠FAC =∠EBA ．∵1tan 2FAC ∠=AB =5，∴AEBE =． ……4分过C 点作CH ⊥AF 于点H ， ∵AB =BC ∠AEB =90°， ∴AC =2AE=25． ∵1tan 2FAC ∠=， ∴CH =2． ……5分 ∵CH ∥AB AB =BC=5， ∴255FCFC =+． ∴FC=310．…6分 23．解：（1）连接OE ，OF ．∵EF AB ⊥，AB 是O 的直径，∴DOF DOE =∠∠．∵2DOE A =∠∠，A α=∠，∴2DOF α=∠． ………………1分∵FD 为O 的切线，∴OF FD ⊥.∴90OFD ︒=∠. ∴+90D DOF ︒=∠∠.902D α∴∠=︒-． ………………2分 （2）图形如图所示.连接OM .∵AB 为O 的直径，∴O 为AB 中点， 90AEB ∠=︒．∵M 为BE 的中点，∴OM AE ∥，1=2OM AE . ………………3分∵30A ∠=︒，∴30MOB A ∠=∠=︒．∵260DOF A ∠=∠=︒ ， ∴90MOF ∠=︒. ………………4分∴222+OM OF MF =．设O 的半径为r ．∵90AEB ∠=︒，30A ∠=︒，∴cos30AE AB ︒=⋅=.∴OM ．…………5分∵FM222)+r =.解得=2r ．（舍去负根）∴O 的半径为2．………DADAABCDEO23. （1）AB 与⊙O 的位置关系是相切 ·················································································· 1分证明：如图，连接OC ． OA OB =，C 为AB 的中点，OC AB ∴⊥．∴AB 是⊙O 的切线． ······································································································· 2分 （2）ED 是直径，90ECD ∴∠=．∴90E ODC ∠+∠=．又90BCD OCD ∠+∠=，OCD ODC ∠=∠， ∴BCD E ∠=∠． 又CBD EBC ∠=∠， ∴BCD BEC △∽△．BC BDBE BC∴=． ∴2BC BD BE =⋅．··········································································································· 3分1tan 2E ∠=，∴12CD EC =． BCD BEC △∽△，∴12BD CD BC EC ==． ············································································································ 4分 设BD x =，则2BC x =． 又2BC BD BE =⋅， ∴2(2)(6)x x x =+． 解得10x =，22x =．0BD x =>，∴2BD =．235OA OB BD OD ∴==+=+=． ·············································································· 5分23.(1)∵BA=BC ，AO=CO, ∴BD ⊥AC. ∵CE 是⊙O 的切线, ∴CE ⊥AC.∴CE ∥BD. ……………………………………1分 ∴∠ECB=∠CBD. ∵BC 平分∠DBE, ∴∠CBE=∠CBD. ∴∠ECB=∠CBE.∴BE=CE. …………………………………………2分 (2)解：作EF ⊥BC 于F. …………………………3分 ∵⊙O 的直径长8， ∴CO=4.∴sin ∠CBD= sin ∠BCE= 45=OC BC. …………………………………………………………4分 ∴BC=5，OB=3. ∵BE=CE, ∴BF=1522BC =. ∵∠BOC=∠BFE=90°，∠CBO=∠EBF, ∴△CBO ∽△EBF.∴BE BF BC OB =. ∴BE=256. ……………………………………………………………………………………5分24．（1）证明：连接AO ，并延长交⊙O 于点E ，交BC 于点F ．∵AB =AC ，∴=AB AC ．∴AE ⊥BC ． ∵AD ∥BC ， ∴AE ⊥AD ．∴AD 是⊙O 的切线．…………… 2分（2）解法1：∵AD ∥BC ， ∴∠D =∠1．∵sin ∠D =35， ∴sin ∠1=35． ∵AE ⊥BC ， ∴OF OB =35． ∵⊙O 的半径OB =15， ∴OF =9，BF =12． ∴AF =24．∴AB= 5分3解法2：过B 作BH ⊥DA 交DA 延长线于H ．E∵AE ⊥AD ，sin ∠D =35， ∴OA OD =35． ∵⊙O 的半径OA =15，∴OD =25，AD =20．∴BD =40．∴BH =24，DH =32．∴AH =12．∴AB = 5分23. （本小题满分5分）（1）证明：连接OC ，∵射线DC 切⊙O 于点C ， ∴∠OCP =90°∵DE ⊥AP ，∴∠DEP =90°∴∠P +∠D =90°，∠P +∠COB =90°∴∠COB =∠D …………………1分∵OA =OC , ∴∠A =∠OCA∵∠COB=∠A +∠OCA ∴∠COB =2∠A∴∠D =2∠A …………………2分（2）解：由（1）可知：∠OCP =90°，∠COP =∠D ， ∴cos ∠COP =cos ∠D =35， …………………3∵CH ⊥OP ，∴∠CHO =90°，设⊙O 的半径为r ，则OH =r ﹣2．在Rt △CHO 中，cos ∠HOC =OH OC =2r r-=35， ∴r =5， …………………4分 ∴OH =5﹣2=3，∴由勾股定理可知：CH =4，∴AH =AB ﹣HB =10﹣2=8．在Rt △AHC 中，∠CHA =90°，∴由勾股定理可知：AC =…………………5分23．（1）证明：∵BD 平分∠ABC ，∴∠1＝∠2.∵DE ∥AB ，∴∠2＝∠3.∴∠1＝∠3.∵BC 是⊙O 的切线，∴∠BDF ＝90°. ∴∠1+∠F ＝90°，∠3+∠EDF ＝90°. ∴∠F ＝∠EDF .∴EF =DE . （2）解：连接CD .∵BD 为⊙O 的直径，∴∠BCD ＝90°.∵DE ∥AB ，∴∠DEF ＝∠ABC .∵cos∠ABC=35，∴在Rt△ECD中，cos∠DEC=CEDE=35.设CE=3x，则DE=5x .由（1）可知，BE= EF=5x.∴BF=10x，CF=2x.在Rt△CFD中，由勾股定理得DF=．∵半径为5，∴BD=10.∵BF×DC= FD×BD，∴1041025x x x=，解得x=.∴DF ==5. …….…….……………5分（其他证法或解法相应给分.）23. （1）证明：连接OC.∵CD CB=∴∠1=∠3.∵OA OC=，∴∠1=∠2.∴∠3=∠2.∴AE OC∥.∵AE EF⊥，∴OC EF⊥.∵OC是O的半径，∴EF是O的切线. ----------------------2分（2）∵AB为O的直径，∴∠ACB=90°.根据勾股定理，由AB=5,BC=3,可求得AC=4.∵AE EF⊥，∴∠AEC=90°.∴△AEC∽△ACB.∴AE AC AC AB=.∴445AE =. ∴165AE =. ----------------------5分 25.（1）证明：∵AB =BC ，∠A =45°，∴∠ACB =∠A =45°．∴∠ABC =90°． …………………………………………………………1分∵AB 是⊙O 的直径，∴BC 是⊙O 的切线． …………………………………………………2分（2）求解思路如下：①连接AD ，由AB 为直径可知，∠ADB =90°，进而可知∠BAD =∠CBD ；……3分 ②由BD =m ，tan ∠CBD =n ，在Rt △ABD 中，可求AD =m n；………………………4分 ③在Rt △ABD 中，由勾股定理可求AB 的长． ……………………………………5分25.解： (1)连结OM.∵BM 平分∠ABC∴∠1 = ∠2 又OM=OB∴∠2 = ∠3∴ OM ∥ BC …………………………………2′AE 是BC 边上的高线∴AE ⊥BC,∴AM ⊥OM∴AM 是⊙O 的切线…………………………………3′（2）∵AB=AC∴∠ABC = ∠C AE ⊥BC,∴E 是BC 中点 ∴EC=BE=3∵cosC=52=ACEC ∴AC=25EC= 215 …………………………………4′ ∵OM ∥ BC ，∠AOM =∠ABE ∴△AOM ∽△ABE ∴ABAO BE OM = 又∠ABC = ∠C ∴∠AOM =∠C 在Rt △AOM 中cos ∠AOM = cosC=52 52=AO OM ∴AO=OM 25 AB=OM 25+OB=OM 27 而AB= AC= 215∴OM 27=215 OM=715 ∴⊙O 的半径是715 …………………………………6′。

2017年北京市房山区中考数学一模试卷一、选择题（本大题共10小题，每小题3分，共30分）1．实数a、b、c、d在数轴上的对应点的位置如图所示,在这四个数中，绝对值最小的数是（）A．a B．b C．c D．d2．下列图案是轴对称图形的是( ）A．B．C．D．3．北京地铁燕房线，是北京地铁房山线的西延线，现正在紧张施工，通车后将是中国大陆第二条全自动无人驾驶线路,预测初期客流量日均132300人次，将132300用科学记数法表示为( ）A．1。

323×105B．1。

323×104C．1.3×105 D．1.323×1064．如图，直线a∥b，三角板的直角顶点放在直线b上,两直角边与直线a相交，如果∠1=55°,那么∠2等于（）A．65°B．55°C．45°D．35°5．如图，A，B，C,D是四位同学画出的一个空心圆柱的主视图和俯视图,正确的一组是（）A．A B．B C．C D．D6．一个不透明的盒子中装有2个白球,5个红球和8个黄球，这些球除颜色外，没有任何其他区别，从这个盒子中随机摸出一个球，摸到红球的概率为( ）A．B．C．D．7．雷达二维平面定位的主要原理是：测量目标的两个信息﹣﹣距离和角度，目标的表示方法为（γ，α）,其中，γ表示目标与探测器的距离；α表示以正东为始边，逆时针旋转后的角度．如图，雷达探测器显示在点A，B,C处有目标出现,其中，目标A的位置表示为A （5,30°)，目标B的位置表示为F(4，150°）．用这种方法表示目标C的位置，正确的是( ）A．(﹣3，300°）B．(3，60°)C．（3，300°）D．（﹣3,60°）8．2022年将在北京﹣﹣张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市,某校开设了冰球选修课,12名同学被分成甲、乙两组进行训练，他们的身高（单位:cm）如表所示：队员1队员2队员3队员4队员5队员6甲组176177175176177175乙组178175170174183176设两队队员身高的平均数依次为甲，乙，方差依次为S甲2，S乙2，下列关系中正确的是（）A．甲=乙，S甲2＜S乙2B．甲=乙,S甲2＞S乙2C．甲＜乙，S甲2＜S乙2D．甲＞乙，S甲2＞S乙29．在同一平面直角坐标系中，正确表示函数y=kx+k(k≠0）与y=(k≠0）的图象的是（）A．B．C．D．10．如图1，已知点E，F,G，H是矩形ABCD各边的中点,AB=6，BC=8,动点M从点E出发，沿E→F→G→H→E匀速运动，设点M运动的路程x，点M到矩形的某一个顶点的距离为y，如果表示y关于x函数关系的图象如图2所示，那么这个顶点是矩形的（)A．点A B．点B C．点C D．点D二、填空题（本小题共6小题，每小题3分，共18分）11．二次根式有意义，则x的取值范围是．12．分解因式：2m2﹣18= ．13．如图中的四边形均为矩形,根据图形，利用图中的字母,写出一个正确的等式: ．14．《九章算术》是我国古代最重要的数学著作之一，在“勾股”章，记载了一道“折竹抵地"问题，叙述为：“今有竹高一丈，末折抵地，去本三尺，问折者几何?”翻译成数学问题是：在Rt△ABC中,∠ACB=90°，AC+AB=10，BC=3，求AC的长，如果设AC=x，可列出的方程为．15．中国国家邮政局公布的数据显示,2016年中国快递业务量突破313.5亿件，同比增长51。

圆的综合题1. 如图，AB 是⊙O 的弦，AB ＝4，过圆心O 的直线垂直AB 于点D ，交⊙O 于点C 和点E ，连接AC 、BC 、OB ，cos ∠ACB ＝13，延长OE 到点F ，使EF ＝2OE .(1)求证：∠BOE ＝∠ACB ; (2)求⊙O 的半径；(3)求证：BF 是⊙O 的切线．2. 如图，AB 为⊙O 的直径，点C 为圆外一点，连接AC 、 BC ，分别与⊙O 相交于点D 、点E ，且»»AD DE ，过点D 作DF ⊥BC 于点F ，连接BD 、DE 、AE . (1)求证：DF 是⊙O 的切线；(2)试判断△DEC 的形状，并说明理由；(3)若⊙O 的半径为5，AC ＝12，求sin ∠EAB 的值．3. (2016长沙9分)如图，四边形ABCD 内接于⊙O ，对角线AC 为⊙O的直径，过点C作AC的垂线交AD的延长线于点E，点F为CE的中点，连接DB，DC，DF.(1)求∠CDE的度数；(2)求证：DF是⊙O的切线；(3)若AC＝25DE，求tan∠ABD的值．4. (2016德州10分)如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC 于点D，过点E作直线l∥BC.(1)判断直线l与⊙O的位置关系，并说明理由；(2)若∠ABC的平分线BF交AD于点F，求证：BE＝EF;(3)在(2)的条件下，若DE＝4，DF＝3，求AF的长．5. (2015永州)如图，已知△ABC内接于⊙O，且AB＝AC，直径AD交BC于点E，F是OE上的一点，使CF∥BD.(1)求证：BE ＝CE ；(2)试判断四边形BFCD 的形状，并说明理由； (3)若BC ＝8，AD ＝10，求CD 的长．6 (2017原创)如图，AB 切⊙O 于点B ，AD 交⊙O 于点C 和点D ，点E 为»DC的中点，连接OE 交CD 于点F ，连接BE 交CD 于点G .(1) 求证：AB ＝AG ；(2) (2)若DG ＝DE ，求证：GB 2＝GC ·GA ；(3)在(2)的条件下，若tan D ＝34，EG ＝10，求⊙O 的半径．7.(2015达州)在△ABC 的外接圆⊙O 中，△ABC 的外角平分线CD 交⊙O 于点D ，F 为»AD 上一点，且»»AF BC ，连接DF ，并延长DF 交BA 的延长线于点E. (1)判断DB 与DA 的数量关系，并说明理由；(2)求证：△BCD ≌△AFD ；(3)若∠ACM ＝120°，⊙O 的半径为5，DC ＝6，求DE 的长．8. 如图，AB 为⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，CG 是⊙O 的弦，CG ⊥AB ，垂足为点D .(1)求证：△ACD ∽△ABC ；(2)求证：∠PCA ＝∠ABC ；(3)过点A 作AE ∥PC 交⊙O 于点E ，交CG 于点F ，连接BE ，若sin P ＝35，CF ＝5，求BE 的长．9、(2016大庆9分)如图，在Rt △ABC 中，∠C ＝90°，以BC 为直径的⊙O 交斜边AB于点M，若H是AC的中点，连接MH。

平谷区2017年初三统一练习（一）一、选择题(本题共30分，每小题3分)1．为解决“最后一公里”的交通接驳问题，平谷区投放了大量公租自行车供市民使用．据统计，目前我区共有公租自行车3 500辆．将3 500用科学记数法表示应为 A ．0.35×104 B ． 3.5×103C ．3.5×102D ． 35×1022．把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A ，则点A 对应的数是A ．1 B． C． D ．23．右图是某几何体从不同角度看到的图形，这个几何体是A ．圆锥B ．圆柱C ．正三棱柱D ．三棱锥4．如果x+y =4，那么代数式222222x yx y x y ---的值是A ．﹣2B ．2C ．12 D ．12- 5．下列图形中，既是轴对称图形，又是中心对称图形的是A ．B ．C ．D ．6．某商场一楼与二楼之间的手扶电梯如图所示．其中AB 、CD 分别表示一楼、二楼地面的水平线，∠ABC =150°，BC 的长是8 m ，则乘电梯从点B 到点C 上升的高度h 是A．B ．8 m CmD ．4 m7．在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：“今有凫（凫：野鸭）起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日相逢？”意思是：野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海．野鸭与大雁从南海和北海同时起飞，经过几天相遇．设野鸭与大雁从南海和北海同时起飞，经过x 天相遇，根据题意，下面所列方程正确的是A ．1)79(=-xB.1)79(=+xC. 1)9171(=+xD. 1)9171(=-x8．如图，是利用平面直角坐标系画出的天安门广场的平面示意图，若这个坐标系分别以正东、 正北方向为x 轴、y 轴的正方向， 表示国旗杆的点的坐标为(0，2.5)， 表示中国国家博物馆的点的坐标为(4，1)， 则表示下列建筑的点的坐标正确的是A ．天安门(0， 4)B ．人民大会堂(﹣4，1)C ．毛主席纪念堂(﹣1，﹣3)D ．正阳门(0，﹣5)主视图 左视图 俯视图9．1-7月份，某种蔬菜每斤的进价与每斤的售价的信息如图所示，则出售该种蔬菜每斤利润最大的月份是A．3月份B．4月份C．5月份D．6月份10．AQI 是空气质量指数（Air Quality Index ）的简称，是描述空气质量状况的指数．其数值越大说明空气污染状况越严重，对人体的健康危害也就越大．AQI 共分六级，空气污染指数为0－50一级优，51－100二级良，101－150三级轻度污染，151－200四级中度污染，201－300五级重度污染，大于300六级严重污染．小明查阅了2015年和2016年某市全年的AQI 指数，并绘制了如下统计图，并得出以下结论：①2016年重度污染的天数比2015年有所减少；②2016年空气质量优良的天数比2015年有所增加；③ 2015年和2016年AQI 指数的中位数都集中在51－100这一档中；④2016年中度污染的天数比2015年多13天．以上结论正确的是A ． ①③B ． ①④C ．②③ D ．②④ 二、填空题(本题共18分，每小题3分) 11．如果分式31-+x x 的值为0，那么x 的值是 ． 12．如图，一个正方形被分成两个正方形和两个一模一样的矩形，请根据图形，写出一个含有a ，b 的正确的等式 ．13．请写出一个在各自象限内，y 的值随x 值的增大而增大的反比例函数表达式 ．14．一个猜想是否正确，科学家们要经过反复的论证．下表是几位科学家“掷硬币”的实验 请根据以上数据，估计硬币出现正面朝上的概率为 （精确到）．15．如图，圆桌面正上方的灯泡发出的光线照射桌面后，在地面上形成阴影（圆形）．已知灯泡距离地面2.4m ，桌面距离地面0.8m （桌面厚度不计算），若桌面的面积是1.2m²，则地面上的阴影面积是 m²． 16．小米是一个爱动脑筋的孩子，他用如下方法作∠AOB 的角平分线： 作法：如图，（1）在射线OA 上任取一点C ，过点C 作CD ∥OB ；（2）以点C 为圆心，CO 的长为半径作弧，交CD 于点E ；（3）作射线OE ．所以射线OE 就是∠AOB 的角平分线．请回答：小米的作图依据是____________________________ ____________________________________________________．三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程. 17．计算：012cos302017︒-．18．解不等式组32,211,52-≤⎧⎪++⎨<⎪⎩x x x x 并写出它的所有非负整数解．．．．．．19．如图，在矩形ABCD 中，点E 是BC 上一点，且DE =DA ，AF ⊥DE 于F ，求证：AF=CD ．20．已知关于x 的一元二次方程x 2-(m +2)x +2m =0．（1）求证：方程总有两个实数根； （2）当m =2时，求方程的两个根． 21．在平面直角坐标xOy 中，直线()10y kx k =+≠与双曲线()0my m x=≠的一个交点为A （﹣2，3），与x 轴交于点B ．(1) 求m 的值和点B 的坐标；(2) 点P 在y 轴上，点P 到直线()10y kx k =+≠，直接写出点P 的坐标．22．随着人们“节能环保，绿色出行”意识的增强，越来越多的人喜欢骑自行车出行．某自行车厂生产的某型号自行车去年销售总额为8万元．今年该型号自行车每辆售价预计比去年降低200元．若该型号车的销售数量与去年相同，那么今年的销售总额将比去年减少10%，求该型号自行车去年每辆售价多少元？23．如图，在△ABC中，BD平分∠ABC交AC于D，EF垂直平分BD，分别交AB，BC，BD于E，F，G，连接DE，DF．（1）求证：DE=DF；（2）若∠ABC=30°，∠C=45°，DE=4，求CF的长．24．阅读以下材料：2017年1月28日至2月1日农历正月初一至初五，平谷区政府在占地面积6万平方米的琴湖公园举办主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会．本次庙会共设置了文艺展演区、非遗展示互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区．展区总面积1720平方米．文艺展演区占地面积600平方米，占展区总面积的34.9％；非遗展示区占地190平方米，占展区总面积的11.0％；特色商品区占地面积是文艺展演区的一半，占展区总面积的17.4％；特色美食区占地200平方米，占展区总面积的11.6％；还有孩子们喜爱的儿童娱乐游艺区．此次庙会本着弘扬、挖掘、展示平谷春节及民俗文化，以京津冀不同地域的特色文化为出发点，全面展示平谷风土人情及津冀人文特色．大年初一，来自全国各地的约3.2万人踏着新春的脚步，揭开了首届平谷庙会的帷幕．大年初二尽管天气寒冷，市民逛庙会热情不减，又约有4.3万人次参观了庙会，品尝特色美食，观看绿都古韵、秧歌表演、天桥绝活，一路猜灯谜、赏图片展，场面火爆．琳琅满目的泥塑、木版画、剪纸、年画等民俗作品也让游客爱不释手，纷纷购买．大年初三，单日接待游客约4万人次，大年初四风和日丽的天气让庙会进入游园高峰，单日接待量较前日增长了约50%．大年初五，活动进入尾声，但庙会现场仍然人头攒动，仍约有5.5万人次来园参观．（1）直接写出扇形统计图中m的值；（2）初四这天，庙会接待游客量约_______万人次；（3）请用统计图或统计表，将庙会期间每日接待游客的人数表示出来．25．如图，⊙O为等腰三角形ABC的外接圆，AB=AC，AD是⊙O的直径，切线DE 与AC的延长线相交于点E．（1）求证：DE∥BC；（2）若DF=n ，∠BAC =2α，写出求CE 长的思路．26．有这样一个问题：探究函数y x =+的图象与性质．小军根据学习函数的经验，对函数y x =+的图象与性质进行了探究． 下面是小军的探究过程， 请补充完整：（1）函数y x =+的自变量x 的取值范围是 ；在平面直角坐标系xOy 中， 描出了以上表中各对对应值为坐标的点，根据描出的点， 画出该函数的图象；（3）观察图象，函数的最小值是 ； （4）进一步探究，结合函数的图象， 写出该函数的一条．．性质（函数最小值除外）： ．27．直线33y x =-+与x 轴，y轴分别交于A ，B 两点，点A 关于直线1x =-的对称点为点C ． （1）求点C 的坐标；（2）若抛物线()230y mx nx m m =+-≠经过A ，B ，C 三点，求该抛物线的表达式；（3）若抛物线()230y ax bx a =++≠ 经过A ，B 两点，且顶点在第二象限，抛物线与线段AC 有两个公共点，求a 的取值范围．28．在△ABC 中，AB =AC ，∠A =60°，点D 是BC 边的中点，作射线DE ，与边AB 交于点E ，射线DE 绕点D 顺时针旋转120°，与直线AC 交于点F ．（1）依题意将图1补全；（2）小华通过观察、实验提出猜想：在点E 运动的过程中，始终有DE=DF ．小华把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：想法1：由点D 是BC 边的中点，通过构造一边的平行线，利用全等三角形，可证DE =DF ；想法2：利用等边三角形的对称性，作点E 关于线段AD 的对称点P ，由∠BAC 与∠EDF 互补，可得∠AED 与∠AFD 互补，由等角对等边，可证DE =DF ；想法3：由等腰三角形三线合一，可得AD 是∠BAC 的角平分线，由角平分线定理，构造点D 到AB ，AC 的高，利用全等三角形，可证DE =DF …….请你参考上面的想法，帮助小华证明DE =DF （选一种方法即可）； （3）在点E 运动的过程中，直接写出BE ，CF ，AB 之间的数量关系．29．在平面直角坐标系中，点Q 为坐标系上任意一点，某图形上的所有点在∠Q 的内部（含角的边），这时我们把∠Q 的最小角叫做该图形的视角．如图1，矩形ABCD ，作射线OA ，OB，则称∠AOB 为矩形ABCD 的视角．（1）如图1，矩形ABCD ，A （﹣3，1），B （3，1），C （3，3），D （﹣3，3），直接写出视角∠AOB 的度数；（2）在（1）的条件下，在射线CB 上有一点Q ，使得矩形ABCD 的视角∠AQB =60°，求点Q 的坐标；（3）如图2，⊙P 的半径为1，点P （1，3），点Q 在x 轴上，且⊙P 的视角∠EQF 的度数大于60°，若Q （a ，0），求a 的取值范围．平谷区2016—2017学年度初三统练（一）数学答案 2017.4图1图1 图2备用图备用图11．3；12．()2222+=++a b a ab b ； 13．答案不唯一，如1y x=-；14．0.50； 15．2.7； 16．两直线平行，内错角相等； (1)等腰三角形两底角相等； ················································································· 3 （其他正确依据也可以）．三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）解答应写出文字说明、演算步骤或证明过程.17．解：020173021231-︒+--cos121- .......................................................................... 4 =﹣2． .. (5)18．解：322 112 5①②-≤⎧⎪⎨++<⎪⎩x x x x ，解不等式①得x ≤1， ··············································································· 1 解不等式②得x ＞﹣3， ··········································································· 2 ∴不等式组的解集是：﹣3＜x ≤1． ······························································· 3 ∴不等式组的非负整数解为0，1．······························································· 5 19．证明：∵矩形ABCD ，∴AD ∥BC ．∴∠ADE =∠DEC ． ····································· 1 ∵AF ⊥DE 于F ，∴∠AFD =∠C =90°． ··································· 2 ∵DE =DA ， ··············································· 3 ∴△ADF ≌△DEC ．···································· 4 ∴AF =CD ． ··············································· 5 20．（1）证明: ∵ Δ=[-(m +2)]2-4×2m ····· (1)=(m -2)2∵ (m -2)2≥0，∴方程总有两个实数根． (2)（2）当m =2时，原方程变为x 2-4x +4=0． ··························································· 3 解得x 1=x 2=2． ························································································· 5 21．解：（1）∵双曲线()0my m x=≠经过点，A （﹣2，3）， ∴6=-m ． ···················································································· 1 ∵直线()10y kx k =+≠经过点A （﹣2，3），∴1=-k ． ····················································································· 2 ∴此直线与x 轴交点B 的坐标为（1，0）. ············································ 3 （2）(0，3)，(0，-1)． ························· (5)22．解：设去年该型号自行车每辆售价x 元，则今年每辆售价为（x ﹣200）元． (1)由题意，得()%8000011080000200-=-x x ，····························································· 2 解得：x =2000． ······················································································ 3 经检验，x =2000是原方程的根． ································································ 4 答：去年该型号自行车每辆售价为2000元． · (5)23．（1）证明：∵EF 垂直平分BD ，∴EB=ED ，FB=FD ． ················································································ 1 ∵BD 平分∠ABC 交AC 于D ， ∴∠ABD =∠CBD ．∵∠ABD +∠BEG =90°，∠CBD +∠BFG =90°，∴∠BEG =∠BFG ．∴BE=BF ． ∴四边形BFDE 是菱形． ∴DE=DF ． ···························································································· 2 （2）解：过D 作DH ⊥CF 于H ． ∵四边形BFDE 是菱形， ∴DF ∥AB ，DE=DF =4．在Rt △DFH 中，∠DFC =∠ABC =30°， ∴DH =2．∴FH =32． .......................................................................................... 3 在Rt △CDH 中，∠C =45°， ∴DH=HC =2． ......................................................................................... 4 ∴CF =2+32． (5)24．（1）扇形统计图中m 的值是25.1%； (1)（2）6； ...................................................................................................... 2 （3）如图． . (5)25．（1）证明：∵AB =AC ，AD 是⊙O 的直径，∴AD ⊥BC 于F ． ····················································································· 1 ∵DE 是⊙O 的切线， ∴DE ⊥AD 于D ．2 ∴DE ∥BC ． ···························································································· 2 （2）连结CD ．由AB =AC ，∠BAC =2α，可知∠BAD =α． ···················································· 3 由同弧所对的圆周角，可知∠BCD =∠BAD=α． 由AD ⊥BC ，∠BCD =α，DF=n ， 根据sin α=DFCD，可知CD 的长． ··············· 4 由勾股定理，可知CF 的长由DE ∥BC ，可知∠CDE =∠BCD ． 由AD 是⊙O 的直径，可知∠ACD =90°． 由∠CDE =∠BCD ，∠ECD =∠CFD ， 可知△CDF ∽△DEC ，可知DF CF=CE CD，可求CE 的长． .............................. 5 26．（1）2x ≥-； . (1)（2）该函数的图象如图所示； (3)（3） ................................................................................................. 4 （4）该函数的其它性质:当20x -≤<时，y 随x 的增大而减小； (5)（答案不唯一，符合函数性质即可写出一条即可）27．解：（1）令y =0，得x =1．∴点A 的坐标为（1,0）． ··································································· 1 ∵点A 关于直线x =﹣1对称点为点C ， ∴点C 的坐标为（﹣3,0）． ·················· 2 （2）令x =0，得y =3．∴点B 的坐标为（0,3）． ∵抛物线经过点B ， ∴﹣3m =3，解得m =﹣1． (3)∵抛物线经过点A ， ∴m+n ﹣3m =0，解得n =﹣2．∴抛物线表达式为223y x x =--+． (4)（3）由题意可知，a <0．根据抛物线的对称性，当抛物线经过（﹣1,0）时，开口最小，a =﹣3， ·········· 5 此时抛物线顶点在y 轴上，不符合题意.当抛物线经过（﹣3,0）时，开口最大，a =﹣1. ········ (6)结合函数图像可知，a 的取值范围为31a -<≤-. (7)28．解：（1）如图1， (1)（2）想法1证明：如图2，过D 作DG ∥AB ，交AC 于G ， ····································· 2 ∵点D 是BC 边的中点，∴DG =12AB ． ∴△CDG 是等边三角形．∴∠EDB +∠EDG=120°．∵∠FDG +∠EDG=120°，∴∠EDB =∠FDG ． ·················································································· 3 ∵BD=DG ，∠B =∠FGD =60°，∴△BDE ≌△GDF ． ················································································· 4 ∴DE =DF ． ····························································································· 5 想法2证明：如图3，连接AD ，∵点D 是BC 边的中点，∴AD 是△ABC 的对称轴．作点E 关于线段AD 的对称点P ，点P 在边AC 上， ········································ 2 ∴△ADE ≌△ADP ．∴DE=DP ，∠AED =∠APD ．∵∠BAC +∠EDF =180°，∴∠AED +∠AFD =180°．∵∠APD +∠DPF =180°，∴∠AFD =∠DPF ． ··················································································· 3 ∴DP=DF ． ···························································································· 4 ∴DE =DF ． ····························································································· 5 想法3证明：如图4，连接AD ，过D 作DM ⊥AB 于M ，DN ⊥AB 于N ， ············· 2 ∵点D 是BC 边的中点，∴AD 平分∠BAC ．∵DM ⊥AB 于M ，DN ⊥AB 于N ，∴DM=DN ． ···························································································· 3 ∵∠A =60°，图1图2图3图4∴∠MDE +∠EDN=120°．∵∠FDN +∠EDN=120°，∴∠MDE=∠FDN ．∴Rt △MDE ≌Rt △NDF ． ............................................................................. 4 ∴DE =DF ． (5)（3）当点F 在AC 边上时，12BE CF AB +=； ·........................................... 6 当点F 在AC 延长线上时，12BE CF AB -=． .. (7)29．解：（1）120°； ............................................................................................ 1 （2）连结AC ，在射线CB 上截取CQ=CA ，连结AQ ． .................................... 2 ∵AB =23，BC =2， ∴AC =4． .......................... 3 ∴∠ACQ =60°． ∴△ACQ 为等边三角形， 即∠AQC =60°． ................ 4 ∵CQ =AC =4， ∴Q （3，﹣1）． ............. 5 （3） 如图1，当点Q 与点O 重合时，∠EQF=60°， ∴Q （0，0）． ................................................................................ 6 如图2，当FQ ⊥x 轴时，∠EQF=60°， ∴Q （2，0）． ................................................................................ 7 ∴a 的取值范围是0＜a ＜2． (8)图2图1。

类型1：圆基础（1）求角度 1、（海淀一模7）如图，AB 为⊙O 的直径，点C 在⊙O 上，若∠ACO =50°，则∠B 的度数为（ ）A ．60°B ．50°C ．40°D ．30°2、（石景山二模6）如图，四边形ABCD 是⊙O 的内接正方形，点P 是劣弧上任意一点（与点B 不重合），则BPC ∠的度数为（ ） A ．30°B ．45°C ．60°D ．90°3、（怀柔二模8）如图，若AB 是⊙O 的直径，CD 是⊙O 的弦，∠ABD =58°，则∠BCD 的度数为（ ）A ．32°B ．58°C ．64°D ．116°4、（苏州中考9）如图，在Rt △ABC 中，∠ACB =90°，∠A=56°．以BC 为直径的⊙O 交AB 于点D ，E 是⊙O 上一点，且 CECD =，连接OE ，过点E 作EF ⊥OE ，交AC 的延长线于点F ，则∠F 的度数为（ ）A ．92B ．108C ．112D ．1245、（西城一模14）如图，四边形ABCD 是⊙O 内接四边形，若∠BAC =30°，∠CBD =80°，则∠BCD 的度数为____________． 6、（朝阳一模13）如图，⊙O 是△ABC 的外接圆，∠ACO=45°，则∠B 的度数为___________．7、（昌平二模12）如图，四边形ABCD 的顶点均在⊙O 上，∠A =70°，则∠C =___________°.8、（青岛中考13）如图，在四边形 ABCD 中，∠ABC ＝∠ADC ＝90°，E 为对角线AC 的中点，连接BE 、ED 、BD ，若∠BAD ＝58°，则∠EBD 的度数为__________度．COABOADBC第13题图9、（丰台一模14）如下图，小量角器的0°刻度线在大量角器的0°刻度线上，且小量角器的中心在大量角器的外缘边上．如果它们外缘边上的公共点P 在大量角器上对应的度数为40°，那么在小量角器上对应的度数为______________．（只考虑小于90°的角度）10、（北京中考14）如图，AB 为O 的直径，C D 、为O 上的点，AD CD =.若040CAB ∠=，则CAD ∠= ． 11、（怀柔二模13）一个扇形的半径长为5，且圆心角为60°，则此扇形的弧长为___________．12、（房山二模13）如图，四边形ABCD 的顶点均在⊙O 上，⊙O 的半径为2. 如果∠D =45°，那么»AC 的长为__________.(结果用π表示)*13、（海淀二模10）利用量角器可以制作“锐角正弦值速查卡”．制作方法如下：如图，设OA =1，以O 为圆心，分别以0.05，0.1，0.15，0.2，…，0.9，0.95长为半径作半圆，再以OA 为直径作⊙M ．利用“锐角正弦值速查卡”可以读出相应锐角正弦的近似值．例如：A ．70°B ．50°C ．40°D ．30°P（2）求线段长 1、（门头沟一模7）如图，AB 是⊙O 的弦，当半径4OA =,120AOB ∠=︒时，弦AB 的长（ ） A ．2 B ．4 C． D．2、（燕山一模7）如图，⊙O 的半径长3cm ，点C 在⊙O 上，弦AB 垂直平分OC 于点D ，则弦AB 的长为（ ）A ．29cm B ．233cm C．33cmD ．49cm第1题图 第2题图 第3题图 第4题图 3、（海淀二模7）如图，OA 为⊙O 的半径，弦BC ⊥OA 于P 点．若OA =5，AP =2，则弦BC的长为（ ）A ．10B ．8C ．6D ．4 4、（朝阳二模9）如图，⊙O 的半径OC 垂直于弦AB ，垂足为D ，OA =，∠B =22.5°，AB的长为（ ）A ．2B ．4C ．D ． 5、（丰台二模7）如图，A ，B ，E 为⊙O 上的点，⊙O 的半径OC ⊥AB 于点D ，已知∠CEB =30°，OD =1，则⊙O 的半径为（ ） A ．3 B ．2 C ．32 D ．4 6、（平谷二模5）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB =30°，⊙O 的半径为6，则圆心O 到弦CD 的距离OE 长为（ ）A ．6B ．5C ．D ．37、（遵义中考17）如图，AB 是⊙O 的直径，AB=4，点M 是OA 的中点，过点M 的直线与⊙O 交于C ，D 两点．若∠CMA=45°，则弦CD 的长为 ． 8、（东城二模14）如图，⊙O 的半径为4，△ABC 是⊙O 的内接三角形，连接OB ，OC ．若∠BAC 与∠BOC 互补，则弦BC 的长为 ．AOBABDOPC BAOEBCD OA9、如图，在平面直角坐标系xOy 中，A （3，4）为⊙O 上一点，B 为⊙O内一点，请写出一个符合要求的点B 的坐标 ． 10、（西城二模14）在平面直角坐标系xOy 中，⊙O 半径是5，点A为⊙O 上一点，AB ⊥x 轴于点B ，AC ⊥y 轴于点C ，若四边形ABOC 面积为12，写出一个符合条件的点A 坐标 .（3）求面积1、（西城二模8）如图，以点O 为圆心，AB 为直径的半圆经过点C ，若C 为弧AB 的中点，若AB =2，则图中阴影部分的面积是（ ）A ．2πB ．122π+C ．4πD ．124π+2、（石景山二模13）如图，ABC △是⊙O 的内接正三角形，图中阴影部分 的面积是12π，则⊙O 的半径为 ．3、（山西中考10）右图是某商品的标志图案，AC 与BD 是O 的两条直径，首尾顺次连接点,,,A B C D ，得到四边形ABCD ．若10,36AC cm BAC =∠= ，则图中阴影部分的面积为（ ）A ．25cm πB ．210cm πC ．215cm πD ．220cm π4、（丰台二模15）如图，扇形纸扇完全打开后，外侧两竹条AB ，AC夹角为120°，AB 的长为30cm ，无贴纸部分AD 的长为10cm ，则贴纸部分的面积等于 cm 2. 5、（东城二模15）如图，一扇形纸扇完全打开后，外侧两竹条AB 和AC 的夹角为120°，竹条AB 的长为25cm ，贴纸部分的宽BD 为15cm ，若纸扇两面贴纸，则一面贴纸的面积为 cm 2. （结果保留π）*6、（河南中考10）如图，将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，点O ，B 的对应点分别为O′，B′，连接BB′，则图中阴影部分的面积是（ ）A ．2π3B ．2 3﹣π3 C ．2 3﹣2π3D ．4 3﹣2π3*7、（德州中考17）某景区修建一栋复古建筑，其窗户设计如图所示.圆的圆心与矩形对角线的交点重合，且圆与矩形上下两边相切（为上切点），与左右两边相交（，为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域.已知圆的半径为1m ，根据设计要求，若∠EOF =45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为_____________.*8、（成都中考23）已知O 的两条直径,AC BD 互相垂直，分别以,,,AB BC CD DA 为直径向外作半圆得到如图所示的图形.现随机地向该图形内掷一枚小针，记针尖落在阴影区域内的概率为1P ，针尖落在O 内的概率为2P ，则12P P ______________.O ABCD E FG。

平谷区2017年初三统一练习（一）一、选择题(此题共30分，每题3分)1．为解决“最后一千米”的交通接驳问题，平谷区投放了大量公租自行车供市民利用．据统计，目前我区共有公租自行车3 500辆．将3 500用科学记数法表示应为 A ．×104B ． ×103C ．×102D ． 35×1022．把一个边长为1的正方形如下图放在数轴上，以正方形的对角线为半径画弧交数轴于点A ，那么点A 对应的数是A ．1B ．2 C ．3 D ．23．右图是某几何体从不同角度看到的图形，那个几何体是A ．圆锥B ．圆柱C ．正三棱柱D ．三棱锥4．若是x+y =4，那么代数式222222x yx y x y ---的值是A ．﹣2B ．2C ．12 D ．12- 5．以下图形中，既是轴对称图形，又是中心对称图形的是A ．B ．C ．D ．6．某商场一楼与二楼之间的手扶电梯如图所示．其中AB 、CD 别离表示一楼、二楼地面的水平线，∠ABC =150°，BC 的长是8 m ，那么乘电梯从点B 到点C 上升的高度h 是A ．43mB ．8 mC ．833mD ．4 m7．在我国古代数学高作《九章算术》中记载了一道有趣的数学问题：“今有凫（凫：野鸭）起南海，七日至北海；雁起北海，九日至南海.今凫雁俱起，问何日重逢？”意思是：野鸭从南海起飞，7天飞到北海；大雁从北海起飞，9天飞到南海．野鸭与大雁从南海和北海同时起飞，通过几天相遇．设野鸭与大雁从南海和北海同时起飞，通过x 天相遇，依照题意，下面所列方程正确的选项是A-1321C D150° h 主视图 左视图 俯视图A ．1)79(=-xB.1)79(=+xC. 1)9171(=+xD. 1)9171(=-x8．如图，是利用平面直角坐标系画出的天安门广场的平面示用意，假设那个坐标系别离以正东、 正北方向为x 轴、y 轴的正方向， 表示国旗杆的点的坐标为(0，， 表示中国国家博物馆的点的坐标为(4，1)， 那么表示以下建筑的点的坐标正确的选项是A ．天安门(0， 4)B ．人民大会堂(﹣4，1)C ．毛主席纪念堂(﹣1，﹣3)D ．正阳门(0，﹣5)9．1-7月份，某种蔬菜每斤的进价与每斤的售价的信息如下图，那么出售该种蔬菜每斤利润最大的月份是A ．3月份B ．4月份C ．5月份D ．6月份10．AQI 是空气质量指数（Air Quality Index ）的简称，是描述状况的指数．其数值越大说明空气污染状况越严峻，对人体的健康危害也就越大．AQI 共分六级，空气污染指数为0－50一级优，51－100二级良，101－150三级轻度污染，151－200四级中度污染，201－300五级重度污染，大于300六级严峻污染．小明查阅了2021年和2016年某市全年的AQI 指数，并绘制了如下统计图，并得出以下结论：①2016年重度污染的天数比2021年有所减少；②2016年空气质量优良的天数比2021年有所增加；③ 2021年和2016年AQI 指数的中位数都集中在51－100这一档中；④2016年中度污染的天数比2021年多13天．以上结论正确的选项是A ． ①③B ． ①④C ．②③D ．②④ 二、填空题(此题共18分，每题3分) 11．若是分式31-+x x 的值为0，那么x 的值是 ． 12．如图，一个正方形被分成两个正方形和两个一模一样的矩形，请依照图形，写出一个含有a ，b 的正确的等式 ．bbaa13．请写出一个在各自象限内，y 的值随x 值的增大而增大的反比例函数表达式 ． 实验者德·摩根 蒲丰 费勒 皮尔逊 罗曼诺夫斯基掷币次数6 140 4 040 10 000 36 000 80 640 出现“正面朝上”的次数 3 109 2 048 4 97918 03139 699 频率请依照以上数据，估量硬币显现正面朝上的概率为 （精准到）．15．如图，圆桌面正上方的灯泡发出的光线照射桌面后，在地面上形成阴影（圆形）．已知灯泡距离地面，桌面距离地面（桌面厚度不计算），假设桌面的面积是²，那么地面上的阴影面积是 m²．16．小米是一个爱动脑筋的小孩，他用如下方式作∠AOB 的角平分线：作法：如图，（1）在射线OA 上任取一点C ，过点C 作CD ∥OB ； （2）以点C 为圆心，CO 的长为半径作弧，交CD 于点E ； （3）作射线OE ．因此射线OE 确实是∠AOB 的角平分线． 请回答：小米的作图依据是____________________________ ____________________________________________________．三、解答题（此题共72分，第17-26题，每题5分，第27题7分，第28题7分，第29题8分）解许诺写出文字说明、演算步骤或证明进程. 17．计算：013122cos302017--+︒-．18．解不等式组32,211,52-≤⎧⎪++⎨<⎪⎩x x x x 并写出它的所有非负整数解．．．．．．19．如图，在矩形ABCD 中，点E 是BC 上一点，且DE =DA ，AF ⊥DE 于F ，求证：AF=CD ．20．已知关于x 的一元二次方程x 2-(m +2)x +2m =0．F OE DC BA（1）求证：方程总有两个实数根； （2）当m =2时，求方程的两个根．21．在平面直角坐标xOy 中，直线()10y kx k =+≠与双曲线()0my m x=≠的一个交点为A （﹣2，3），与x 轴交于点B ． (1) 求m 的值和点B 的坐标；(2) 点P 在y 轴上，点P 到直线()10y kx k =+≠P 的坐标．22．随着人们“节能环保，绿色出行”生产的某型号自行车去年销售总额为8行车去年每辆售价多少元？23．如图，在△ABC 中，BD 平分∠ABC 交AC 于D ，EF 垂直平分BD ，别离交AB ，BC ，BD 于E ，F ，G ，连接DE ，DF ．（1）求证：DE=DF ； （2）假设∠ABC =30°，∠C =45°，DE =4，求CF 的长．24．阅读以下材料：2017年1月28日至2月1日农历正月初一至初五，平谷区政府在占地面积6万平方米的琴湖公园举行主题为“逛平谷庙会乐百姓生活”的平谷区首届春节庙会．本次庙会共设置了文艺展演区、非遗展现互动区、特色商品区、儿童娱乐游艺区、特色美食区等五个不同主题的展区．展区总面积1720平方米．文艺展演区占地面积600平方米，占展区总面积的％；非遗展现区占地190平方米，占展区总面积的％；特色商品区占地面积是文艺展演区的一半，占展区总面积的％；特色美食区占地200平方米，占展区总面积的％；还有小孩们喜爱的儿童娱乐游艺区．这次庙会本着宏扬、挖掘、展现平谷春节及风俗文化，以京津冀不同地域的特色文化为起点，全面展现平谷风土人情及津冀人文特色．大年初一，来自全国各地的约万人踏着新春的脚步，揭开了首届平谷庙会的帷幕．大年初二尽管天气严寒，市民逛庙会热情不减，又约有万人次参观了庙会，品尝特色美食，观看绿都古韵、秧歌演出、天桥绝活，一路猜灯谜、赏图片展，场面火爆．琳琅满目的泥塑、木版画、剪纸、年画等风俗作品也让游客爱不释手，纷纷购买．大年初三，单日接待游客约4万人次，大年初四风和日丽的天气让庙会进入游园顶峰，单日接待量较前日增加了约50%．大年初五，活动进入尾声，但庙会现场仍然人头攒动，仍约有万人次来园参观．（1）直接写出扇形统计图中m 的值；（2）初四此日，庙会接待游客量约_______万人次；（3）请用统计图或统计表，将庙会期间每日接待游客的人数表示出来．25．如图，⊙O 为等腰三角形ABC 的外接圆，AB =AC ，AD 是⊙O 的直径，切线DE 与AC 的延长线相交于点E ． （1）求证：DE ∥BC ；（2）假设DF=n ，∠BAC =2α，写出求CE 长的思路．F E BD OAC26．有如此一个问题：探讨函数+2y x x =-+的图象与性质．小军依照学习函数的体会， 对函数+2y x x =-+的图象与性质进行了探讨． 下面是小军的探讨进程， 请补充完整：（1）函数+2y x x =-+的自变量x 的取值范围是 ； x ﹣2 ﹣ ﹣ ﹣1 ﹣ 01 2 3 4 … y2﹣﹣﹣…在平面直角坐标系xOy 中， 描出了以上表中各对对应值为坐标的点，依照描出的点， 画出该函数的图象；yx–3–2–11234–2–112345O（3）观看图象，函数的最小值是 ；（4）进一步探讨，结合函数的图象， 写出该函数的一条．．性质（函数最小值除外）： ．27．直线33y x =-+与x 轴，y 轴别离交于A ，B 两点，点A 关于直线1x =-的对称点为点C ． （1）求点C 的坐标；yx–2–112345–5–4–3–2–112O（2）若抛物线()230y mx nx m m =+-≠通过A ，B ，C 三点，求该抛物线的表达式；（3）若抛物线()230y ax bx a =++≠ 通过A ，B 两点，且极点在第二象限，抛物线与线段AC 有两个公共点，求a 的取值范围．28．在△ABC 中，AB =AC ，∠A =60°，点D 是BC 边的中点，作射线DE ，与边AB 交于点E ，射线DE 绕点D 顺时针旋转120°，与直线AC 交于点F ． （1）依题意将图1补全；（2）小华通过观看、实验提出猜想：在点E 运动的进程中，始终有DE=DF ．小华把那个猜想与同窗们进行交流，通过讨论，形成了证明该猜想的几种方式：方式1：由点D 是BC 边的中点，通过构造一边的平行线，利用全等三角形，可证DE =DF ； 方式2：利用等边三角形的对称性，作点E 关于线段AD 的对称点P ，由∠BAC 与∠EDF 互补，可得∠AED 与∠AFD 互补，由等角对等边，可证DE =DF ；方式3：由等腰三角形三线合一，可得AD 是∠BAC 的角平分线，由角平分线定理，构造点D 到AB ，AC 的高，利用全等三角形，可证DE =DF …….请你参考上面的方式，帮忙小华证明DE =DF （选一种方式即可）； （3）在点E 运动的进程中，直接写出BE ，CF ，AB 之间的数量关系．29．在平面直角坐标系中，点Q 为坐标系上任意一点，某图形上的所有点在∠Q 的内部（含角的边），这时咱们把∠Q 的最小角叫做该图形的视角．如图1，矩形ABCD ，作射线OA ，OB ，那么称∠AOB 为矩形ABCD 的视角．图1 备用图（1）如图1，矩形ABCD ，A（﹣3，1），B （3，1），C （3，3），D （﹣3，3），直接写出视角∠AOB 的度数；（2）在（1）的条件下，在射线CB 上有一点Q ，使得矩形ABCD 的视角∠AQB =60°，求点Q 的坐标；（3）如图2，⊙P 的半径为1，点P （1，3），点Q 在x 轴上，且⊙P 的视角∠EQF 的度数大于60°，假设Q （a ，0），求a 的取值范围．平谷区2016—2017学年度初三统练（一）数学答案一、选择题(此题共30分，每题3分)题号 1 2 3 4 5 6 7 8 9 10 答案BBACDDCBAC二、填空题（此题共18分，每题3分）11．3；12．()2222+=++a b a ab b ； 13．答案不唯一，如1y x=-；14．； 15．； 16．两直线平行，内错角相等； ·············································································· 1 等腰三角形两底角相等； ················································································· 3 （其他正确依据也能够）．三、解答题（此题共72分，第17-26题，每题5分，第27题7分，第28题7分，第29题8分）解许诺写出文字说明、演算步骤或证明进程. 17．解：020173021231-︒+--cos=33123212--+⨯- ·········································································· 4 图1图2备用图=﹣2． (5)18．解：322 11 2 5①②-≤⎧⎪⎨++<⎪⎩x x x x ，解不等式①得x ≤1， ··············································································· 1 解不等式②得x ＞﹣3， ··········································································· 2 ∴不等式组的解集是：﹣3＜x ≤1． ······························································· 3 ∴不等式组的非负整数解为0，1．······························································· 5 19．证明：∵矩形ABCD ，∴AD ∥BC ．∴∠ADE =∠DEC ． ····································· 1 ∵AF ⊥DE 于F ，∴∠AFD =∠C =90°． ··································· 2 ∵DE =DA ， ··············································· 3 ∴△ADF ≌△DEC ．···································· 4 ∴AF =CD ． ·.............................................. 5 20．（1）证明: ∵ Δ=[-(m +2)]2-4×2m .. (1)=(m -2)2 ∵ (m -2)2≥0，∴方程总有两个实数根． (2)（2）当m =2时，原方程变成x 2-4x +4=0． ··························································· 3 解得x 1=x 2=2． · (5)21．解：（1）∵双曲线()0my m x=≠通过点，A （﹣2，3）， ∴6=-m ． ···················································································· 1 ∵直线()10y kx k =+≠通过点A （﹣2，3），∴1=-k ． ..................................................................................... 2 ∴此直线与x 轴交点B 的坐标为（1，0）. ............................................ 3 （2）(0，3)，(0，-1)． (5)22．解：设去年该型号自行车每辆售价x 元，那么今年每辆售价为（x ﹣200）元． (1)由题意，得()%8000011080000200-=-x x ，····························································· 2 解得：x =2000． ······················································································ 3 经查验，x =2000是原方程的根． ································································ 4 答：去年该型号自行车每辆售价为2000元． ················································ 5 F23．（1）证明：∵EF 垂直平分BD ，∴EB=ED ，FB=FD ． ················································································ 1 ∵BD 平分∠ABC 交AC 于D ， ∴∠ABD =∠CBD ．∵∠ABD +∠BEG =90°，∠CBD +∠BFG =90°，∴∠BEG =∠BFG ．∴BE=BF ． ∴四边形BFDE 是菱形． ∴DE=DF ． ···························································································· 2 （2）解：过D 作DH ⊥CF 于H ． ∵四边形BFDE 是菱形， ∴DF ∥AB ，DE=DF =4．在Rt △DFH 中，∠DFC =∠ABC =30°， ∴DH =2．∴FH =32． .......................................................................................... 3 在Rt △CDH 中，∠C =45°， ∴DH=HC =2． ......................................................................................... 4 ∴CF =2+32． (5)24．（1）扇形统计图中m 的值是%； (1)（2）6； ...................................................................................................... 2 （3）如图． . (5)25．（1）证明：∵AB =AC ，AD 是⊙O 的直径，∴AD ⊥BC 于F ． ..................................................................................... 1 ∵DE 是⊙O 的切线， ∴DE ⊥AD 于D ．2 ∴DE ∥BC ． .. (2)E G D（2）连结CD ．由AB =AC ，∠BAC =2α，可知∠BAD =α． ···················································· 3 由同弧所对的圆周角，可知∠BCD =∠BAD=α． 由AD ⊥BC ，∠BCD =α，DF=n ， 依照sin α=DFCD，可知CD 的长． ··············· 4 由勾股定理，可知CF 的长由DE ∥BC ，可知∠CDE =∠BCD ． 由AD 是⊙O 的直径，可知∠ACD =90°． 由∠CDE =∠BCD ，∠ECD =∠CFD ， 可知△CDF ∽△DEC ，可知DF CF=CE CD，可求CE 的长． .............................. 5 26．（1）2x ≥-； . (1)（2）该函数的图象如下图； (3)yx–3–2–11234–2–112345O（3）-2 ................................................................................................. 4 （4）该函数的其它性质:当20x -≤<时，y 随x 的增大而减小； (5)（答案不唯一，符合函数性质即可写出一条即可）27．解：（1）令y =0，得x =1．∴点A 的坐标为（1,0）． ··································································· 1 ∵点A 关于直线x =﹣1对称点为点C ， ∴点C 的坐标为（﹣3,0）． ·················· 2 （2）令x =0，得y =3．∴点B 的坐标为（0,3）． ∵抛物线通过点B ， ∴﹣3m =3，解得m =﹣1． (3)∵抛物线通过点A ， ∴m+n ﹣3m =0，解得n =﹣2．∴抛物线表达式为223y x x =--+． (4)（3）由题意可知，a <0．依照抛物线的对称性，当抛物线通过（﹣1,0）时，开口最小，a =﹣3， (5)F BO C y x–2–112345–4–3–2–112A B C O现在抛物线极点在y 轴上，不符合题意.当抛物线通过（﹣3,0）时，开口最大，a =﹣1. (6)结合函数图像可知，a 的取值范围为31a -<≤-. (7)28．解：（1）如图1， (1)（2）方式1证明：如图2，过D 作DG ∥AB ，交AC 于G ， (2)∵点D 是BC 边的中点， ∴DG =12AB ． ∴△CDG 是等边三角形． ∴∠EDB +∠EDG=120°． ∵∠FDG +∠EDG=120°， ∴∠EDB =∠FDG ． ·················································································· 3 ∵BD=DG ，∠B =∠FGD =60°， ∴△BDE ≌△GDF ． ················································································· 4 ∴DE =DF ． ····························································································· 5 方式2证明：如图3，连接AD ， ∵点D 是BC 边的中点， ∴AD 是△ABC 的对称轴．作点E 关于线段AD 的对称点P ，点P 在边AC 上， ········································ 2 ∴△ADE ≌△ADP ．∴DE=DP ，∠AED =∠APD ． ∵∠BAC +∠EDF =180°， ∴∠AED +∠AFD =180°． ∵∠APD +∠DPF =180°， ∴∠AFD =∠DPF ． ................................................................................... 3 ∴DP=DF ． .. (4)图2图3图4图1∴DE =DF ． ····························································································· 5 方式3证明：如图4，连接AD ，过D 作DM ⊥AB 于M ，DN ⊥AB 于N ， ············· 2 ∵点D 是BC 边的中点， ∴AD 平分∠BAC ．∵DM ⊥AB 于M ，DN ⊥AB 于N ， ∴DM=DN ． ···························································································· 3 ∵∠A =60°，∴∠MDE +∠EDN=120°． ∵∠FDN +∠EDN=120°， ∴∠MDE=∠FDN ．∴Rt △MDE ≌Rt △NDF ． ············································································· 4 ∴DE =DF ． ····························································································· 5 （3）当点F 在AC 边上时，12BE CF AB +=； ············································ 6 当点F 在AC 延长线上时，12BE CF AB -=． (7)29．解：（1）120°； (1)（2）连结AC ，在射线CB 上截取CQ=CA ，连结AQ ． (2)∵AB =23，BC =2，∴AC =4． (3)∴∠ACQ =60°．∴△ACQ 为等边三角形， 即∠AQC =60°． ················ 4 ∵CQ =AC =4，∴Q （3，﹣1）． (5)（3）如图1，当点Q 与点O 重合时，∠EQF=60°，图2图1∴Q（0，0）． (6)如图2，当FQ⊥x轴时，∠EQF=60°，∴Q（2，0）． (7)∴a的取值范围是0＜a＜2． (8)。