天津大学版工程力学习题答案(部分)

第 十五 章 压杆稳定思 考 题15−1 在§15−2 中对两端铰支细长压杆，按图a 所示的坐标系及挠曲线形状，推导出了欧拉公式22r c lEI πF试问如分别取图b ，c ，d 所示的坐标系及挠曲线形状时，挠曲线微分方程及所得到的F c r 公式与图a 情况下得到的结果是否相同？ 15−2 欧拉公式在什么范围内适用？如果把中长杆误认为细长杆应用欧拉公式计算其临界力，会导至什么后果？ 15−3 图示8种截面形态的细长压杆，如果各方向的支承条件相同，问压杆失稳时会在哪个方向弯曲？(a)(b)(c)(d)思考题 15−1图思考题15−3图15−4 两根压杆的材料、长度与杆端的支承条件均相同，横截面面积也相同，但其中一个为圆形截面，另一个为正方形截面，问哪一根杆能够承受的压力较大？ 15−5 若两根压杆的材料相同且柔度相等，这两根压杆的临界应力是否一定相等，临界力是否一定相等？15−6 由两个型号相同的不等边角钢组成的中心受压杆件，有下面两种布置方案，在两端约束条件相同的情况下，哪种布置合理，为什么？17−7 与上题类似由两个型号相同的等边角钢组成的中心受压杆件，图中的两种布置方案，哪种布置合理，为什么？15−8 为什么在选择压杆的截面时，必须采用试算方法？习题15−1 图示各杆的材料和截面均相同，试问哪根杆能够承受的压力最大，哪根最小？解：对于材料和截面面积均相同的压杆，柔度λ越大，临界力F c r 越小，因而压杆越容易失稳，亦即能够承受的压力最小。

根据ilμλ=，由于各杆的截面均相同，因此只需比较各杆的计算长度l μ即可（a ） m l 551=⨯=μ （b ） m l 9.477.0=⨯=μ(a)(b)(c)(d) (e)(f)习题15−1图(a) (b)思考题 15−7 图(a) 思考题 15−6 图(b)（c ） m l 5.495.0=⨯=μ （d ） m l 422=⨯=μ （e ） m l 881=⨯=μ（f ） 上、下两段分别计算，临界力应取较小者，而计算长度l μ应取较大者上段 m l 5.255.0=⨯=μ 下段 m l 5.357.0=⨯=μ经比较可得，杆（f ）能够承受的压力最大，杆（e ）能够承受的压力最小。

第十四章 组合变形习 题14−1 截面为20a 工字钢的简支梁，受力如图所示，外力F 通过截面的形心，且与y 轴成φ角。

已知：F =10kN ，l =4m ，φ=15°，[σ]=160MPa ，试校核该梁的强度。

解：kN.m 104104141=⨯⨯==Fl M kN.m;58821510kN.m;65991510.sin φsin M M .cos φcos M M y z =⨯===⨯==查附表得：33cm 531cm 237.W ;W y z ==122.9MPa Pa 109122105311058821023710569966363=⨯=⨯⨯+⨯⨯=+=--....W M W M σy y z z max[]σσmax <，强度满足要求。

14−2 矩形截面木檩条，受力如图所示。

已知：l =4m ，q =2kN/m ，E =9GPa ，[σ]=12MPa ，4326'= α，b =110mm ，h =200mm ，1][=f。

试验算檩条的强度和刚度。

z解：kN.m 4421122=⨯⨯==ql M kN.m;789143264kN.m;578343264.sin φsin M M .cos φcos M M y z ='⨯==='⨯== m ...W ;m ...W y z 42421003341102206110333722011061--⨯=⨯⨯=⨯=⨯⨯=MPa 329Pa 1032910033410789110333710578364343......M M σy y z z max=⨯=⨯⨯+⨯⨯=+=-- []σσmax <，强度满足要求。

m...sin EI φsin ql f m...cos EI φcos ql f y y zz 339434339434109314110220121109384432641025384510034922011011093844326410253845--⨯=⨯⨯⨯⨯⨯'⨯⨯⨯⨯==⨯=⨯⨯⨯⨯⨯'⨯⨯⨯⨯==mm ..f f f y z 4517104517322=⨯=+=-20012291<=l f ，所以挠度满足要求。

⼯程⼒学（天津⼤学）第11章答案（DOC）第⼗⼀章梁弯曲时的变形习题11?1 ⽤积分法求下列简⽀梁A 、B 截⾯的转⾓和跨中截⾯C 点的挠度。

解：（a ）取坐标系如图所⽰。

弯矩⽅程为：x l M M e= 挠曲线近似微分⽅程为：x lM y EI e-='' 积分⼀次和两次分别得：C x lM y EI e +-='22，（a ） D Cx x lM EIy e ++-=36 (b) 边界条件为：x =0时，y =0，x =l 时，y =0，代⼊（a ）、(b)式，得：0,6==D l M C e梁的转⾓和挠度⽅程式分别为：)62(12l M x l M EI y e e +-='，)66(13lx M x l M EI y e e +-= 所以：EIl M y l EI M θEI l M θe C e B e A 16,3,62=AC 段弯矩⽅程为：)20(11lx x lMM e ≤≤=BC段弯矩⽅程为：)2(22l x lM x l M M e e≤≤-=两段的挠曲线近似微分⽅程及其积分分别为：(a)(b)习题11?1图xAC 段：11x lM y EI e-='' 12112C x lM y EI e +-='，（a ） 1113116D x C x lM EIy e ++-= (b) BC 段：e eM x lM y EI +-=''22 22222C M x lM y EI e e ++-='，（c ） 22223226D x C x M x l21212y y y y lx x '='===，时，代⼊（a ）、(b)式、（c ）、(d)式,得：,8D 0,2411,2422121l MD l M C l M C e e e==-==，梁的转⾓和挠度⽅程式分别为：AC 段：)242(121l M x l M EI y e e +-='，)246(11311lx M x l M EI y e e +-= BC 段：)24112(12222l M x M x l M EI y e e e -+-='，)8 241126(12222322l M lx M x M x l M EI y e e e e +-+-=所以：0,24,24===C eB e A y l EIM θEI l M θ11?2 ⽤积分法求下列悬臂梁⾃由端截⾯的转⾓和挠度。

工程力学复习题三铰拱刚架如图所示，受一力偶作用，其矩M=50kN·m ，不计自重，试求A 、B 处的约束反力。

答案：AC 杆为二力杆受力图如(a)所示。

再画整体受力图，如(b)图所示。

Σm=0 R A ·AD=M ∴R A =R B =M AD=50422=17.7kN方向如图所示。

如图所示为二杆桁架，1杆为钢杆，许用应力［σ］1=160MPa ，横截面面积A 1=6cm 2；2杆为木杆，其许用压应力［σ］2=7MPa ，横截面面积A 2=100cm 2。

如果载荷P=40kN ，试校核结构强度。

答案：两杆均为二力杆，取结点A为研究对象，受力图如图所示。

Σy=0,N1sin30°-P=0∴N1=P/sin30°=80kNΣx=0,-N1cos30°+N2=0∴N2=N1cos30°=69.3kN1杆：σ1=NA11328010610=⨯⨯=133MPa<［σ］12杆：σ2=NA22326931010010=⨯⨯.=6.93MPa<［σ］2分析如图所示体系的几何构造。

答案：去掉与地基的连接，只考虑上部结构，几何不变体系，且没有多余约束。

分析如图所示体系的几何构造。

答案：从A点开始依次去掉二元体，可知为几何不变体系且无多余约束。

分析如图所示体系的几何构造。

答案：将折杆画成直杆，上部结构为一个刚片, 用四杆与地基相连。

几何不变有一个多余约束。

求简支梁中点K的竖向位移，EI=常数。

答案：荷载作用的实状态和虚设单位力状态弯矩图分别如图所示：图乘法求得中K 竖向位移：用力法计算下图所示超静定刚架，并作出内力图。

答案：原结构为1次超静定结构。

选取基本体系如图(a)所示，基本方程为1111P 0X δ∆+=。

系数和自由项分别为31156l EIδ=，1P 0∆= 答案得10X =。

内力图分别如图(d)~(f)所示。

2EI EIEIq q1X X 1=1l lll82ql 82ql 2ql 2ql 2ql 2ql P 1图(a) 基本体系M 图M (b)(c)F Q N 图F 图(f)(e)M 图(d)用力法计算下图所示超静定刚架，并作出内力图。

第 十五 章 压杆稳定思 考 题15−1 在§15−2 中对两端铰支细长压杆，按图a 所示的坐标系及挠曲线形状，推导出了欧拉公式22r c lEI πF试问如分别取图b ，c ，d 所示的坐标系及挠曲线形状时，挠曲线微分方程及所得到的F c r 公式与图a 情况下得到的结果是否相同？ 15−2 欧拉公式在什么范围内适用？如果把中长杆误认为细长杆应用欧拉公式计算其临界力，会导至什么后果？ 15−3 图示8种截面形态的细长压杆，如果各方向的支承条件相同，问压杆失稳时会在哪个方向弯曲？(a)(b)(c)(d)思考题 15−1图思考题15−3图15−4 两根压杆的材料、长度与杆端的支承条件均相同，横截面面积也相同，但其中一个为圆形截面，另一个为正方形截面，问哪一根杆能够承受的压力较大？ 15−5 若两根压杆的材料相同且柔度相等，这两根压杆的临界应力是否一定相等，临界力是否一定相等？15−6 由两个型号相同的不等边角钢组成的中心受压杆件，有下面两种布置方案，在两端约束条件相同的情况下，哪种布置合理，为什么？17−7 与上题类似由两个型号相同的等边角钢组成的中心受压杆件，图中的两种布置方案，哪种布置合理，为什么？15−8 为什么在选择压杆的截面时，必须采用试算方法？习题15−1 图示各杆的材料和截面均相同，试问哪根杆能够承受的压力最大，哪根最小？解：对于材料和截面面积均相同的压杆，柔度λ越大，临界力F c r 越小，因而压杆越容易失稳，亦即能够承受的压力最小。

根据ilμλ=，由于各杆的截面均相同，因此只需比较各杆的计算长度l μ即可（a ） m l 551=⨯=μ （b ） m l 9.477.0=⨯=μ(a)(b)(c)(d)(e)(f)习题15−1图(a) (b)思考题 15−7 图(a) 思考题 15−6 图(b)（c ） m l 5.495.0=⨯=μ （d ） m l 422=⨯=μ （e ） m l 881=⨯=μ（f ） 上、下两段分别计算，临界力应取较小者，而计算长度l μ应取较大者上段 m l 5.255.0=⨯=μ 下段 m l 5.357.0=⨯=μ经比较可得，杆（f ）能够承受的压力最大，杆（e ）能够承受的压力最小。

第十二章 用能量法计算弹性位移习 题12−1 两根杆拉伸刚度均为EA ，长度相同，承受荷载如图所示，分布荷载集度q =F/l ，试求这两根杆的应变能，并作比较。

解：EAl F V 221=，EA l F dx EA l )qx (dx EA l F V l l N622202022===⎰⎰ 213V V =12−2 试求图示受扭圆轴内所积蓄的应变能，杆长为l ，直径为d ，材料的剪变模量为G 。

解：4320420232163222Gdl m dx d πGl )mx (dx GI l T V l lP ===⎰⎰ 12−3 试计算下列梁内所积蓄的应变能，略去剪力的影响。

习题12−2图解：（a ）先求支座反力： ql F ,ql F RB RA 8381==以A 为坐标原点，x 1以向右为正，AC 段的弯矩方程为：118x qlM = 以B 为坐标原点，x 2以向左为正，BC 段的弯矩方程为：22222183qx x ql M -= 梁的变形能为：EIl q dx EI )qx qlx (dx EI )qlx (dx EIMdx EI M V l l l l 153601722183282252202222202120222021=-+=+=⎰⎰⎰⎰(b) 以B 为坐标原点，x 以向左为正，AB 段的弯矩方程为：306x lq M =梁的变形能为：EIl q dx EI )l x q (dx EI M V l l 504262520023002===⎰⎰ (c) 以B 为坐标原点，x 以向左为正，AB 段的弯矩方程为：Fx M )x (M +=梁的变形能为：EIl F EI MFl EI l M dx EI )Fx M (dx EI M V l l6222232220202++=+==⎰⎰ (d) 先求支座反力： ,ql F RA 8３=以A 为坐标原点，x 1以向右为正，AB 段的弯矩方程为：21112183qx x ql M -= （0≤x 1≤l ）以C 为坐标原点，x 2以向左为正，BC 段的弯矩方程为：22221qx M -=（0≤x 2≤l /2） 梁的变形能为：EIl q dx EI )qx (dx EI )qx qlx (dx EIMdx EI M V l ll l12803221221832252220222102211202221=-+-=+=⎰⎰⎰⎰12−4 试求图示结构中的弹性变形能。

工程力学复习题参考的答案 天津大学1、利用对称性，计算下图所示各结构的内力，并绘弯矩图。

解：取半结构如图(a)所示，为2次超静定结构。

再取半结构的基本体系如图(b)所示，基本方程为1111221P 2112222P 00X X X X δδ∆δδ∆++=⎧⎪⎨++=⎪⎩ 系数和自由项分别为119EIδ=，1221552EIδδ==，223613EIδ=，1P 13603EI ∆=，2P 1900EI∆=解得17.04kN X =-，214.18kN X =-。

原结构弯矩图如图(f)所示。

C BA10kN/m4m3m4mCBA10kN/m2X1X1X=1112X=133710kN/m80807.04202030.4230.4230.4230.4226.326.31(b) 基本体系M图(c)(a) 半结构PM(e)M图(kN·m)(f)2M图(d)图(kN·m)2、用结点法或截面法求图示桁架各杆的轴力。

解：（1）判断零杆（12根）。

（2）节点法进行内力计算，结果如图。

3、分析如图所示体系的几何构造。

解：从A点开始依次去掉二元体，可知为几何不变体系且无多余约束。

4、试求图示刚架在水压力作用下C、D两点的相对水平位移，各杆EI为常数。

解：（1）作荷载作用下弯矩图：在C、D两点加一对反向的单位水平力，并作弯矩图如下：则：5、某条形基础，宽B=2m ，埋深d=1m 。

基底附加压力p=100kPa ，基底至下卧层顶面的距离Z=2m ，下卧层顶面以上土的重度3/20m kN =γ，经修正后，下卧层地基承载力设计值kPa f 110=，扩散角 22=θ，试通过计算，验算下卧层地基承载力是否满足要求？（4.0tan =θ） 解：kPa d cz 60203)2(=⨯=⨯+=γσ kPa Z b b p z 6.554.02222100tan 20=⨯⨯+⨯=⨯+⨯=θσf kPa z cz >=+=+6.115606.55σσ，故不能满足要求。

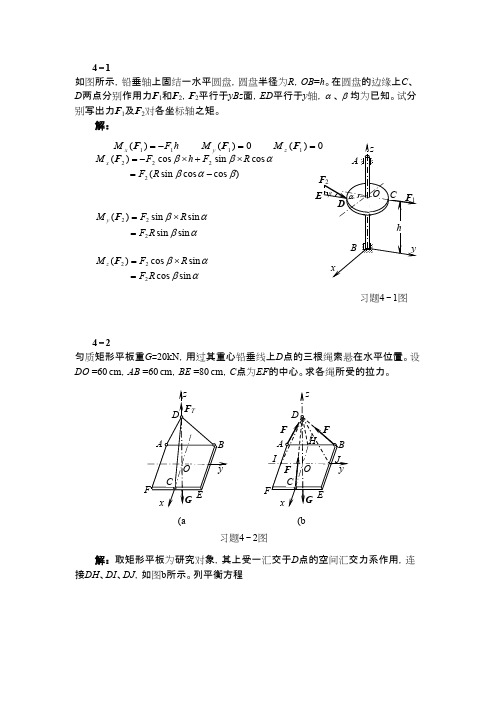
D o n e (略)2−1分别用几何法和解析法求图示四个力的合力。

已知力F 3水平，F 1=60N ，F 2=80N ，F 3=50N ，F 4=100N 。

解： (一) 几何法用力比例尺，按F 3、F 4、F 1、F 2的顺序首尾相连地画出各力矢得到力多边形abcde ，连接封闭边ae 既得合力矢F R ，如图b 所示。

从图上用比例尺量得合力F R 的大小F R =68.8N ，用量角器量得合力F R 与x 轴的夹角θ=88°28′，其位置如图b 所示。

(二) 解析法以汇交点为坐标原点，建立直角坐标系xOy ，如图c 所示。

首先计算合力在坐标轴上的投影N79.68511002180103605121103N85.152100502180101605221101421R 4321R =⨯-⨯+⨯=-+==-=⨯-+⨯+⨯-=-++-==∑∑F F F F F F F F F F F y y x x然后求出合力的大小为N 81.6879.68)85.1(222R 2R R =+-=+=y x F F F设合力F R 与x 轴所夹锐角为θ，则82881838.3785.179.68tan R R '︒====θθxy F F再由F R x 和F R y 的正负号判断出合力F R 应指向左上方，如图c 所示。

习题2−1图 F 1 F 2 F 4 F 3 F R 88°28′ (b) 231 1 1 1 F 1 F 2F 3 F 4 F Rθ (c) 23 1 1 1 1 F 1 F 2 F 3 F 4(a) 0 25 50kN e a b c d O y xD o n e （略） 2−2一个固定的环受到三根绳子拉力F T1 、F T2 、F T3的作用，其中F T1，F T2的方向如图，且F T1=6kN ，F T2=8kN ，今欲使F T1 、F T2 、F T3的合力方向铅垂向下，大小等于15kN ，试确定拉力F T3的大小和方向。