天津大学版工程力学习题答案第二章1

天津大学2021年春季学期《工程力学》在线作业一附参考答案
试卷总分:100 得分:100
一、单选题 (共 20 道试题,共 100 分)
1.一下说法错误的是（）
A.拱主要承受压力，因此可以使用抗拉弱、抗压强的材料
B.拱需要坚实的基础
C.带拉杆三铰拱不是静定拱
D.三铰拱两个水平支座反力互等
答案:C
2.矩形截面梁受均布荷载作用，梁的高为h，宽为b，其跨度为L，若梁的跨度减小一半，问梁的正应力是跨度为L多少倍（）
A.２倍
B.0.5倍
C.0.25倍
D.４倍
答案:C
更多加微boge30619
3.一下关于拱内力图制作错误的是（）
A.需要沿拱的跨度方向将拱轴分为若干等分
B.只需要计算各等分点截面上的内力值
C.需要将已得各截面内力值用曲线光滑连接
D.不管是在均布荷载下还是在集中荷载下，拱的三个内力图都是曲线图形
答案:B
4.{图}
A.A
B.B
C.C
D.D
答案:A
5.{图}
A.A
B.B
C.C
D.D
答案:C
6.弯曲梁，当某截面的剪力Q=0时，( )。

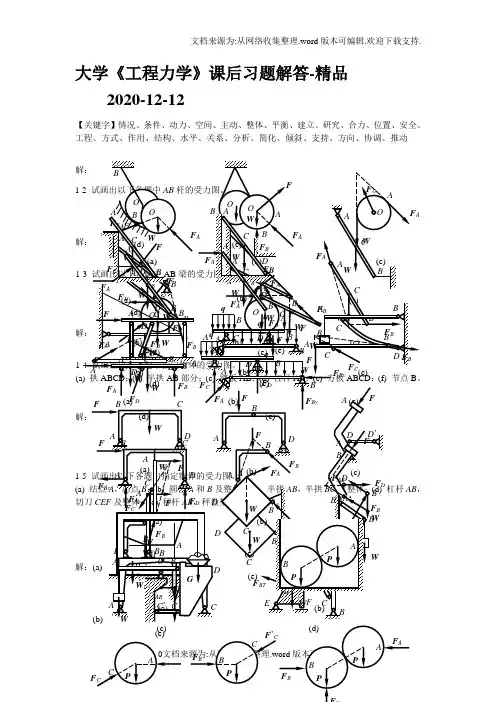
大学《工程力学》课后习题解答-精品2020-12-12【关键字】情况、条件、动力、空间、主动、整体、平衡、建立、研究、合力、位置、安全、工程、方式、作用、结构、水平、关系、分析、简化、倾斜、支持、方向、协调、推动(e)(c)(d)(e)’CD2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点(2) AC 与BC 2-3 水平力F A 和D 处的约束力。

解：(1) 取整体(2) 2-4 在简支梁，力的大小等于20KN ，如图所示。

若解：(1)(2)求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

解：(1) 取DE (2) 取ABC2-7 在四连杆机构ABCD 试求平衡时力F 1和F 2解：（1）取铰链B (2) 取铰链C 由前二式可得：F FF ADF2-9 三根不计重量的杆AB，AC，AD在A点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。

试求在与O D平行的力F作用下，各杆所受的力。

已知F=0.6 kN。

解：(1)间汇交力系；(2)解得：AB、AC3-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。

求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a) (b) (c) 3-2 M ，试求A 和C解：(1) 取 (2) 取 3-3 Nm ，M 2解：(1)(2) 3-5 大小为AB 。

各杆 解：(1)(2)可知：(3) 研究OA 杆，受力分析，画受力图：列平衡方程：AB A3-7 O1和O2圆盘与水平轴AB固连，O1盘垂直z轴，O2盘垂直x轴，盘面上分别作用力偶（F1，F’1），（F2，F’2）如题图所示。

第二章 平面汇交力系与平面力偶系2−1分别用几何法和解析法求图示四个力的合力。

已知力F 3水平，F 1=60N ，F 2=80N ，F 3=50N ，F 4=100N 。

解： (一) 几何法用力比例尺，按F 3、F 4、F 1、F 2的顺序首尾相连地画出各力矢得到力多边形abcde ，连接封闭边ae 既得合力矢F R ，如图b 所示。

从图上用比例尺量得合力F R 的大小F R =68.8N ，用量角器量得合力F R 与x 轴的夹角θ=88°28′，其位置如图b 所示。

(二) 解析法以汇交点为坐标原点，建立直角坐标系xOy ，如图c 所示。

首先计算合力在坐标轴上的投影N79.68511002180103605121103N85.152100502180101605221101421R 4321R =⨯-⨯+⨯=-+==-=⨯-+⨯+⨯-=-++-==∑∑F F F F F F F F F F F y y x x然后求出合力的大小为N 81.6879.68)85.1(222R 2R R =+-=+=y x F F F设合力F R 与x 轴所夹锐角为θ，则82881838.3785.179.68tan R R '︒====θθxy F F再由F R x 和F R y 的正负号判断出合力F R 应指向左上方，如图c 所示。

习题2−1图(b)(c) 2 4(a) 0 25 50kN2−2一个固定的环受到三根绳子拉力F T1 、F T2 、F T3的作用，其中F T1，F T2的方向如图，且F T1=6kN ，F T2=8kN ，今欲使F T1 、F T2 、F T3的合力方向铅垂向下，大小等于15kN ，试确定拉力F T3的大小和方向。

解： 以汇交点为坐标原点，建立直角坐标系xOy ，如图b 所示。

计算合力在坐标轴上的投影)2(15sin 238sin 30cos )1(0cos 21860cos 30sin 332R 3321R -=⨯-⨯--=-︒-===-⨯+=-︒+==∑∑θθθθT RT T y yT T T T x x F F F F F F F F F F F F由式（1）、（2）联立，解得4538,85.123'︒==θkN F T 。

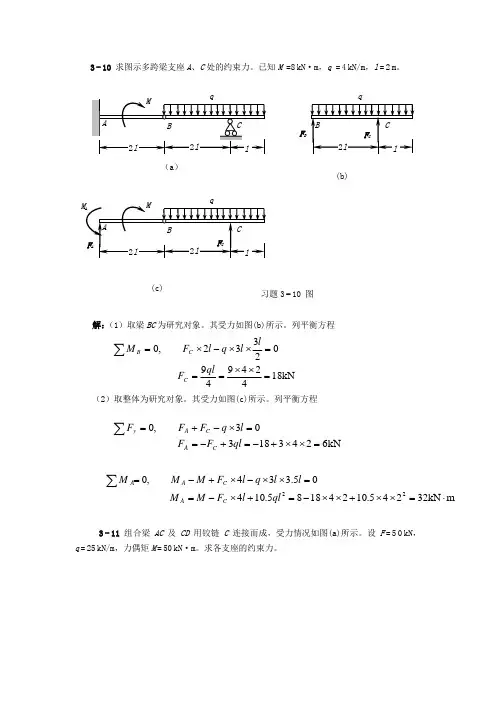
3-10 求图示多跨梁支座A 、C 处的约束力。

已知M =8kN ·m ，q =4kN/m ，l =2m 。

解：（1）取梁BC 为研究对象。

其受力如图(b)所示。

列平衡方程 （2）取整体为研究对象。

其受力如图(c)所示。

列平衡方程3-11 组合梁 AC 及CD 用铰链C 连接而成，受力情况如图(a)所示。

设F =50kN ，q =25kN/m ，力偶矩M =50kN ·m 。

求各支座的约束力。

F BkN1842494902332,0=⨯⨯===⨯⨯-⨯=∑ql F ll q l F M C C B kN624318303,0=⨯⨯+-=+-==⨯-+=∑ql F F l q F F F C A C A ymkN 32245.10241885.10405.334,022⋅=⨯⨯+⨯⨯-=+⨯-==⨯⨯-⨯+-=∑ql l F M M l l q l F M M MC A C A A解：（1）取梁CD 为研究对象。

其受力如图(c)所示。

列平衡方程（2）取梁AC 为研究对象。

其受力如图(b)所示，其中F ′C =F C =25kN 。

列平衡方程F C(b)(c)´CkN 25450252420124,0=+⨯=+==-⨯⨯-⨯=∑M q F M q F MD D CkN 25450256460324,0=-⨯=-==-⨯⨯+⨯-=∑M q F M q F MC C D)kN(25225225250222021212,0↓-=⨯-⨯-='--==⨯'-⨯⨯-⨯+⨯-=∑CA C A BF q F F F q F F MkN150225425650246043212,0=⨯+⨯+='++==⨯'-⨯⨯-⨯-⨯=∑CB CB AF q F F F q F F M6−1作图示杆件的轴力图。

解：在求AB 段内任一截面上的轴力时，在任一截面1−1处截断，取左段为脱离体（图c ），并设轴力F N1为拉力。

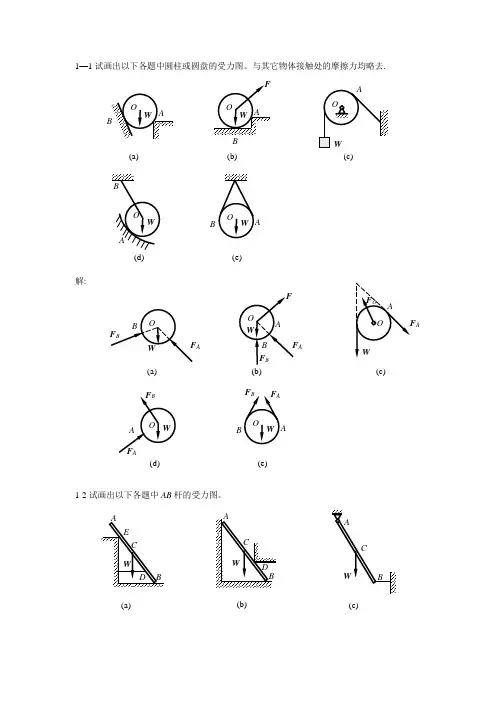
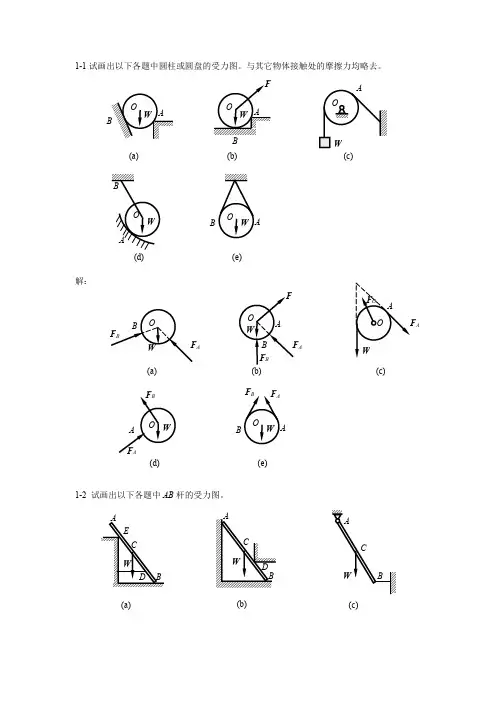
1—1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去. 解:1-2试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3试画出以下各题中AB 梁的受力图.(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解:1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b ） 半拱AB 部分;(c) 踏板AB ；(d ） 杠杆AB;(e) 方板ABCD;(f ） 节点B 。

解:(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b) CB(c)BF D1-5 试画出以下各题中指定物体的受力图.(a ） 结点A ，结点B ；(b) 圆柱A 和B 及整体;(c ） 半拱AB ，半拱BC 及整体；（d) 杠杆AB ，切刀CEF 及整体;（e) 秤杆AB ，秤盘架BCD 及整体。

解：（a)(d)FC(e)WB(f)F FBC(c)(d)AT F BAF (b)(e)（b ）(c ）(d)（e)2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接,如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535N ，不计杆重，试求两杆所受的力。

C AA C’CDDBF 1解：（1）取节点C 为研究对象,画受力图,注意AC 、BC 都为二力杆，（2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2—3 水平力F 作用在刚架的B 点，如图所示.如不计刚架重量，试求支座A 和D 处的约束力。

解:(1） 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形:（2)211 1.1222D A DD A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。

工程力学课后详细答案第一章静力学的基本概念受力图第二章 平面汇交力系2-1解：由解析法，23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故：22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故： 223R RX RY F F F KN=+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ） 由平衡方程有：0X =∑sin 300AC AB F F -=0Y =∑cos300AC F W -=0.577AB F W=（拉力）1.155AC F W=（压力）（b ） 由平衡方程有：0X =∑ cos 700AC AB F F -=0Y =∑sin 700AB F W -=1.064AB F W=（拉力）0.364AC F W=（压力）（c ） 由平衡方程有：0X =∑cos 60cos300AC AB F F -=0Y =∑sin 30sin 600AB AC F F W +-=0.5AB F W= (拉力)0.866AC F W=（压力）（d ） 由平衡方程有：0X =∑sin 30sin 300AB AC F F -=0Y =∑cos30cos300AB AC F F W +-=0.577AB F W= (拉力)0.577AC F W= (拉力)2-4 解：（a ）受力分析如图所示：由x =∑ 22cos 45042RA F P -=+15.8RA F KN∴=由Y =∑22sin 45042RA RB F F P +-=+7.1RB F KN∴=(b)解：受力分析如图所示：由x =∑cos 45cos 45010RA RB F F P --=0Y =∑sin 45sin 45010RA RB F F P -=联立上二式，得：22.410RA RB F KN F KN==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5RA F KN= （压力）5RB F KN=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=-2-7解：受力分析如图所示，取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后，解得：0.707RA F P=0.707RB F P=由二力平衡定理0.707RB CB CBF F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600AB AC F F W +-=联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '= 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=0Y =∑cos 75cos 750AB AD F F P +-=联立后可得： 2cos 75AD AB PF F ==取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD P F F F KN'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=0Y =∑sin sin 300RA F P α-=联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=0Y =∑ 305BC AC F F +⋅=联立上二式得： 1.67AC F KN=（拉力）1.0BC F KN=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑05RD REF F '= 0Y =∑05RD F Q -=联立方程后解得： 5RD F Q =2REF Q '=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=0Y =∑sin 450RB RA F F P --=且RE REF F '=联立上面各式得：RA F =2RB F Q P=+（3）取BCE 部分。

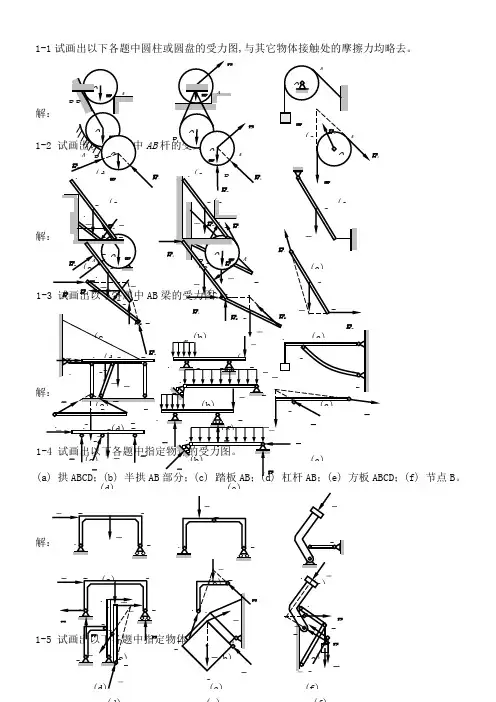
1-1试画出以下各题中圆柱或圆盘的受力图,与其它物体接触处的摩擦力均略去。

(a) 拱ABCD ；(b) 半拱；(f) 节点B 。

(d)F (e)(e)(f)D B C(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(b)(c) F FFFW F C ’Oy(e)2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点CAC 、BC 都为二力杆，(2) AC 与BC 2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1)(2) 2-4 在简支梁20KN ，如图所示。

若梁的自重不计，试求两解：(1) 研究AB(2)相似关系： 几何尺寸： 求出约束反力：2-6 如图所示结构由两弯杆ABC 和DE 构成。

构件重量不计，图中的长度单位为cm 。

已知F =200 N ，试求支座A 和E 的约束力。

F F AF DFF B F Adc e解：(1) 取DE(2) 取ABC2-7 在四连杆机构ABCD F 1和F 2解：（1）取铰链B(2) 取铰链C 2-9 三根不计重量的杆AB ，AC ，AD 在A 点用铰链连接，各杆与水平面的夹角分别为450，，450和600，如图所示。

试求在与O D 平行的力F 作用下，各杆所受的力。

已知F =0.6 kN 。

解：(1) AD 均为二力杆，画受力图，得到一个空(2) 解得：AB 、AC F 23-1 已知梁AB 上作用一力偶，力偶矩为M ，梁长为l ，梁重不计。

求在图a ，b ，c 三种情况下，支座A 和B 的约束力解：(a)B 处的约束力组成一个力偶；列平衡方程：(b) 受力分析，画受力图；处的约束力组成一个力偶；列平衡方程：(c)列平衡方程：3-2M ，试求A 和C 点处的约束力。

工程力学（第2版）第2章 平面力系题库：主观题（1-10）道 + 计算题（11-36）道 + 填空题（37-52）道 + 选择题（53-69）道 + 判断题（70-85）道 一、主观题2-1 如何利用几何法和解析法求平面汇交力系的合力？答案：利用几何法时，可根据力的平行四边形法则或作力多边形得到合力；利用解析法时，可先求Rx x Ry y F F F F ⎧=⎪⎨=⎪⎩∑∑，进而得到()()()()cos ,,cos ,RRx Ry x y R Rx R R Ry RF F F F F F i F F F j F F ⎧=+=+⎪⎨⎪==⎩∑∑ 知识点：2.1节 参考页：P19-P20 学习目标：1 难度：12-2 指出思考题2-2图的各图中，哪个是力系的合力？答案：图（a ），1F 是合力；图（b ），合力为零；图（c ），2F 是合力。

知识点：2.1节 参考页：P19-P20 学习目标：1 难度：22-3 用解析法求合力时，若选不同的直角坐标轴，所得的合力是否相同？答案：当选择不同的坐标轴时，所得力的投影不同，但合力的大小和方向是相同的。

知识点：2.1节 参考页：P20 学习目标：1 难度：22-4 已知某一平面一般力系向A 点简化得到的主矢50 N AF '=，主矩20 N m A M =⋅，试求原力系向B 点简化结果。

其中20 mm AB =。

答案：50 N BA F F ''==0350cos302010 N m A B M F -⎛⎫'=⨯⨯=⋅ ⎪⎝⎭()20 N m A B A B M M M F ⎛⎫'=+=+⋅ ⎪⎝⎭知识点：2.3节参考页：P24 学习目标：3 难度：22-5 思考题2-5图所示力F 和力偶,F F ⎛⎫''' ⎪⎝⎭对轮的作用有何不同？设轮轴静止，2F F F '''=-=。

工程力学复习题参考的答案 天津大学1、利用对称性，计算下图所示各结构的内力，并绘弯矩图。

解：取半结构如图(a)所示，为2次超静定结构。

再取半结构的基本体系如图(b)所示，基本方程为1111221P 2112222P 00X X X X δδ∆δδ∆++=⎧⎪⎨++=⎪⎩ 系数和自由项分别为119EIδ=，1221552EIδδ==，223613EIδ=，1P 13603EI ∆=，2P 1900EI∆=解得17.04kN X =-，214.18kN X =-。

原结构弯矩图如图(f)所示。

C BA10kN/m4m3m4mCBA10kN/m2X1X1X=1112X=133710kN/m80807.04202030.4230.4230.4230.4226.326.31(b) 基本体系M图(c)(a) 半结构PM(e)M图(kN·m)(f)2M图(d)图(kN·m)2、用结点法或截面法求图示桁架各杆的轴力。

解：（1）判断零杆（12根）。

（2）节点法进行内力计算，结果如图。

3、分析如图所示体系的几何构造。

解：从A点开始依次去掉二元体，可知为几何不变体系且无多余约束。

4、试求图示刚架在水压力作用下C、D两点的相对水平位移，各杆EI为常数。

解：（1）作荷载作用下弯矩图：在C、D两点加一对反向的单位水平力，并作弯矩图如下：则：5、某条形基础，宽B=2m ，埋深d=1m 。

基底附加压力p=100kPa ，基底至下卧层顶面的距离Z=2m ，下卧层顶面以上土的重度3/20m kN =γ，经修正后，下卧层地基承载力设计值kPa f 110=，扩散角 22=θ，试通过计算，验算下卧层地基承载力是否满足要求？（4.0tan =θ） 解：kPa d cz 60203)2(=⨯=⨯+=γσ kPa Z b b p z 6.554.02222100tan 20=⨯⨯+⨯=⨯+⨯=θσf kPa z cz >=+=+6.115606.55σσ，故不能满足要求。

范钦珊教育教学工作室FAN Qin-Shan’s Education & Teaching StudioeBook工程力学习题详细解答（教师用书）(第2章)2006-12-18第2章 力系的简化2－1 由作用线处于同一平面内的两个力F 和2F 所组成平行力系如图所示。

二力作用线之间的距离为d 。

试问：这一力系向哪一点简化，所得结果只有合力，而没有合力偶；确定这一合力的大小和方向；说明这一合力矢量属于哪一类矢量。

解：由图(a),假设力系向C 点简化所得结果只有合力，而没有合力偶，于是，有∑=0)(F C M ，02)(=⋅++-x F x d F ，d x =∴，F F F F =-=∴2R ， 方向如图示。

合力矢量属于滑动矢量。

2－2 已知一平面力系对A (3，0)，B (0，4)和C (－4.5，2)三点的主矩分别为：M A 、M B 和M C 。

若已知：M A ＝20 kN.m 、M B ＝0和M C ＝－10kN.m,求：这一力系最后简化所得合力的大小、方向和作用线。

解：由已知M B = 0知合力F R 过B 点；由M A = 20kN ·m ，M C = -10kN ·m 知F R 位于A 、C 间，且 CD AG 2=（图（a ）） 在图（a ）中： 设 OF = d ，则 θcot 4=dCD AG d 2)sin 3(==+θ （1） θθsin )25.4(sin d CE CD -==（2）即 θθs i n )25.4(2s i n)3(dd -=+ d d -=+93 3=d∴ F 点的坐标为（-3, 0） 合力方向如图（a ），作用线如图过B 、F 点； 34tan =θ 8.4546sin 6=⨯==θAG8.4R R ⨯=⨯=F AG F M Ak N 6258.420R ==F 即 )k N 310,25(R =F作用线方程：434+=x y讨论：本题由于已知数值的特殊性，实际G 点与E 点重合。

1-1试画出以下各题中圆柱或圆盘的受力图,与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB杆的受力图。

(a)B(b)(c)(d)A(e)BA(a)(b)A(c)A(d)AA(e)B解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)(e)B(a)B(b)(c)F BF(a)W (c)AF(b)1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

A ’ D ’B ’(d)(e)(a)AF(b)WA (c)(d)F(e)F(a)(b)(c)CD W解：1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

(a)D(b)B(c)BF D(d)FCD (e)WB(f)FF(a)(b)解：(a)(b)(c)AF ABF ATF AF BAFFCAAC(e)(d)(e)’CDWDF C’B2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 oy ACo x BC AC AC BC FF F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

F 1FBC解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2) 由力三角形得211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o的力F ，力的大小等于20KN ，如图所示。

《工程力学》第二章第二章平面基本力系答案一、填空题 ( 将正确答案填写在横线上)1. 平面力系分为平面汇交力系、平面平行力系和平面一般力系.2.共线力系是平面汇交力系地特例 .3.作用于物体上地各力作用线都在同一平面内, 而且都汇交于一点地力系 , 称为平面汇交力系 .4. 若力 FR对某刚体地作用效果与一个力系地对该刚体地作用效果相同, 则称 FR为该力系地合力, 力系中地每个力都是FR地分力 .5.在力地投影中 , 若力平行于 x轴 , 则 F X＝ F 或-F ; 若力平行于 Y轴, 则 Fy＝ F或 -F : 若力垂直于 x轴 , 则Fx=0; 若力垂直于 Y轴, 则 Fy＝ 0 .6.合力在任意坐标轴上地投影 , 等于各分力在同一轴上投影地代数和 .7.平面汇交力系平衡地解析条件为：力系中所有力在任意两坐标轴上投影地代数和均为零. 其表达式为∑ Fx＝ 0 和∑ Fy＝ 0 , 此表达式有称为平面汇交力系地平均方程.8.利用平面汇交力系平衡方程式解题地步骤是：（1）选定研究对象 , 并画出受力图 .（2）选定适当地坐标轴 , 画在受力图上；并作出各个力地投影.（3）列平衡方程 , 求解未知量 .9.平面汇交力系地两个平衡方程式可解两个未知量 . 若求得未知力为负值 , 表示该力地实际指向与受力图所示方向相反 .10.在符合三力平衡条件地平衡刚体上, 三力一定构成平面汇交力系.11.用力拧紧螺丝母 , 其拎紧地程度不仅与力地大小有关, 而且与螺丝母中心到力地作用线地距离有关 .12. 力矩地大小等于力和力臂地乘积,通常规定力使物体绕矩心逆时针转动时力矩为正, 反之为负 .力矩以符号 Mo(F)表示,O点称为距心, 力矩地单位是 N.M .13.由合力矩定力可知 , 平面汇交力系地合力对平面内任一点地力矩 , 等于力系中地各分力对于同一点力矩地代数和 .14.绕定点转动物体地平衡条件是：各力对转动中心O点地矩地代数和等于零 . 用公式表示为∑Mo(Fi) ＝ 0 .15.大小相等、方向相反、作用线平行地二力组成地力系 , 称为力偶 . 力偶中二力之间地距离称为力偶臂 . 力偶所在平面称为力偶作用面 .16.在平面问题中 , 力偶对物体地作用效果 , 以力地大小和力偶臂地乘积来度量 , 这个乘积称为偶距, 用符号M表示.17.力偶三要素是：力偶矩地大小、转向和作用面方位.二、判断题（正确地打“√”, 错误地打“×”）1. 共线力系是平面汇交力系地特殊情形, 但汇交点不能确定 .（√）2.平面汇交力系地合力一定大于任何一个分力.（×）3.力在垂直坐标轴上地投影地绝对值与该力地正交分力大小一定相等.（√）4.力系在平面内任意一坐标轴上投影地代数和为零, 则该力系一定是平衡力系 .（×）5.只要正确地列出平衡方程 , 则无论坐标轴方向及矩心位置如何取定, 未知量地最终计算结果总一致.（√）6.平面汇交力系地合力 , 等于各分力在互相垂直两坐标轴上投影地代数和.（×）7.力矩和力偶都是描述受力物体转动效果地物理量；力矩和力偶地含义和性质完全相同.( ×)8.力对物体地转动效果用力矩来度量, 其常用单位符号为 N﹒ m.（√）9.力矩使物体绕定点转动地效果取决于力地大小和力臂地大小两个方面.（×）10.同时改变力偶中力地大小和力偶臂长短, 而不改变力偶地转向 , 力偶对物体地作用效果就一定不会改变 .(×) 11. 力偶矩地大小和转向决定了力偶对物体地作用效果, 而与矩心地位置无关.（√）三. 选择题（ B） 1.平面汇交力系地合力一定等于________.A.各分力地代数和B.各分力地失量和C.零（ A） 2.如图 2— 1所示地两个三角形,________ 是平衡力系 .A.图aB.图bC.两个都不是（A ）3.力使物体绕定点转动地效果用_______来度量 .A. 力矩B.力偶矩C.力地大小和方向（C ）4.如图 2— 2所示中地 ______正确表示了力 F对 A点之矩 Ma（ F）2FL.（C ）5.力偶可以用一个_______来平衡 .A.力B.力矩C.力偶（C ）6.力矩不为零件地条件是_______.A.作用力不等于零B.力地作用线不通过矩心C.作用力和力臂均不为零（C） 7.如图 2— 3所示地各组力偶中 , 两个力偶等效地是 _______.（ C ） 8. 为便于解题 , 力地投影坐标轴方向一般应按_______选取 , 且将坐标原点与汇交点重合.A.水平或者铅垂B.任意C.尽量与未知力垂直或多数力平行四．简答题1.如图 2—4所示地钢架 ,A 、D两点上地力 F1、F2地作用线交于 B点 , 若在 D点上加力 F3, 并使钢架平衡 , 则力 F3地作用线一定通过哪一点?其指向如何 ?答 : 通过 B点 , 由 B点指向 D点. 因为在主动力 F1地作用下 ,C点地运动趋势方向向上 , 根据三力平衡汇交定理可知 F3地方向是由B点指向 D点 .2. 如图 2-5 所示 , 刚体受两力偶 (F1,F1 ’ ) 和 (F2,F2 ’ ) 作用 , 其力多边形恰好闭合, 刚体处于平衡状态吗 ?答 : 刚体不会平衡 . 因为刚体受力偶 (F1,F1 ’) 和 (F2,F2 ’ )作用产生顺时针方向转动.3.如图 2-6 中 , 半径为 r 地圆盘在力偶 M=Fr地作用下转动 , 如在盘地 r/2 处加一力 F’ , 且 F’ =2F, 便可使圆盘得到平衡, 说明力偶距可用一个力来平衡, 对吗 ?答 : 不对 . 力偶距是由力F’对 O点地产生地距相平衡地.4.按图 2-7 所示 a.b 两种不同地捆法 (a ＜β) 吊起同一重物 , 哪种捆法易断 ?为什么 ?答 :a 图易断 . 计算起吊重物地钢丝绳强度时, 应考虑起吊重物上升时地加速度, 因为此时钢丝绳所受地拉力最大, 应加上一定地安全系数.如图所示 a＜ 120°且越小越好; 当 a=180时, 钢丝绳受力无穷大, 无法保证其工作地安全性.5.结合图 2-8 所示地实例说明里偶地等效性 .答：力偶地等效性有：(1)只要保持力偶矩大小和转向不变 , 力偶可在其作用面内任意移动 , 而不改变其作用效应 .(2)只要保持力偶距大小和转向不变 , 可以同时改变力偶中力地大小和力偶臂地长短 , 其作用效果不变 .图中 d1<d2, 若 F1×d2=F2×d1, 只要 F2>F1, 丝锥地转动效应会保持不变.五．计算题1.如图 2— 9所示 , 已知： F1＝ F2＝ F3＝F4＝40N . 试分别求出各力在X,Y 轴上地投影 .解 : F1x＝ F1·cos30°＝ 34.64NF1y ＝ F1·cos30 °＝ 20NF2x＝ 0F2y＝－ F2＝－ 40NF3x＝－ F3＝－ 40NF3y＝ 0F4x＝－ F4·cos135 °＝－ 28.28NF y＝ F·cos45 °＝ 28.28N2.试求图 2— 10所示中各力在 X轴和 Y轴上地投影 . 已知 F1＝ F2＝ F4＝ 100N,F 3＝F5＝ 150N , F6＝200N . 解: F1x＝ F1＝ 100NF1y＝ 0NF2x＝ 0NF2y＝ F2＝ 100NF3x＝ F3·cos30 °＝ 129.9NF3y＝ F3·cos60 °＝ 75NF4x＝ F4·cos60 °＝ 50NF4y＝－ F4·cos150 °＝－ 86.6NF5x＝ F5·cos60 °＝ 75NF5y＝－F5·cos150 ＝°－ 129.9NF6x＝－ F6·cos120 °＝－ 100NF6y＝－ F6·cos150 °＝－ 173.2N3.试求图 2— 11所示中各力分别对 O点和对 A点地力矩 .( 用代数式表示 )解： Mo(F 1) ＝ F1×1＝ F1M A(F1) ＝－ F1×1＝－ F1Mo(F 2) ＝－ F2×2＝－ 2F2M A(F2) ＝－ F2×4＝－ 4F2Mo(F 3) ＝ F3×0＝ 0M A(F3) ＝ F3×1×sin45＝°0.707F3 Mo(F 4) ＝ F4×3＝ 3F4M A(F4) ＝ F4×4＝ 4F4Mo(F 5) ＝ F5×1.141＝1.141F5M A(F5) ＝－ F5×1×sin45 ＝°－ 0.707F54. 计算图 2— 12所示中力 F对B点地力矩 . 已知 F＝ 50N,la ＝0.6m ,a＝ 30°.（ a) M B(F) ＝ F1·la＝ 30N·m（b) M B(F) ＝ F1·la ·cosa ＝25.98N ·m5.如图 2—13所示矩形板 ABCD中 , AB ＝ 100mm,BC ＝ 80mm,若力 F＝10N,a ＝ 30°.试分别计算力 F对 A、B、 C、 D各点地力矩 .解： M A(F)0N mM B(F)F AB sin10 1001500N mm2M C(F)F cos BC F sin AB10380101100192.8 N mm22M D(F) F cos AD031080 692.8 N mm26.如图 2—15所示 , 已知： F＝ 100N,La ＝80mm,Lb ＝ 15mm. 试求力 F对点 A地力矩 .解 :(a) M A(F )F cos30l b F sin 30l a100315100180 2.701N m22（ b）M A(F ) F cos60l a F sin 60l b100180 100315 5.299N m227.如图 2-15 所示为拖拉机制动装置 , 制动时用力 F踩踏板 , 通过拉杆 CD而使拖拉机制动 .设F=100N,踏板和拉杆自重不计 . 求图示位置拉杆地拉力 FD及铰链支座 B地约束反力 .解 :(1) 取踏板 ABC为研究对象由三力平衡定理可知:B 点地约束反力FB通过汇交点O,如图所示以 O点为坐标原点建立坐标系.(2)做投影Fx＝－ F·cos135°＝－ 0.707F F ＝－ F·cos135°＝－ 0.707FYF x＝ FD F＝ 0D DYF x＝－ F ·cos135 ＝°－ 0.866FB FBY＝ F ·cos60 °＝0.5FBB B B(3)列方程由Σ Fix ＝0 : Fx+F D x+F B x＝ 0由Σ Fi Y＝ 0 : F Y +F DY +F BY＝ 0(4)解方程解方程得到 : F D＝ 193.2NF B＝ 141.2N。

D o n e (略)2−1分别用几何法和解析法求图示四个力的合力。

已知力F 3水平，F 1=60N ，F 2=80N ，F 3=50N ，F 4=100N 。

解： (一) 几何法用力比例尺，按F 3、F 4、F 1、F 2的顺序首尾相连地画出各力矢得到力多边形abcde ，连接封闭边ae 既得合力矢F R ，如图b 所示。

从图上用比例尺量得合力F R 的大小F R =68.8N ，用量角器量得合力F R 与x 轴的夹角θ=88°28′，其位置如图b 所示。

(二) 解析法以汇交点为坐标原点，建立直角坐标系xOy ，如图c 所示。

首先计算合力在坐标轴上的投影N79.68511002180103605121103N85.152100502180101605221101421R 4321R =⨯-⨯+⨯=-+==-=⨯-+⨯+⨯-=-++-==∑∑F F F F F F F F F F F y y x x然后求出合力的大小为N 81.6879.68)85.1(222R 2R R =+-=+=y x F F F设合力F R 与x 轴所夹锐角为θ，则82881838.3785.179.68tan R R '︒====θθxy F F再由F R x 和F R y 的正负号判断出合力F R 应指向左上方，如图c 所示。

习题2−1图 F 1 F 2 F 4 F 3 F R 88°28′ (b) 231 1 1 1 F 1 F 2F 3 F 4 F Rθ (c) 23 1 1 1 1 F 1 F 2 F 3 F 4(a) 0 25 50kN e a b c d O y xD o n e （略） 2−2一个固定的环受到三根绳子拉力F T1 、F T2 、F T3的作用，其中F T1，F T2的方向如图，且F T1=6kN ，F T2=8kN ，今欲使F T1 、F T2 、F T3的合力方向铅垂向下，大小等于15kN ，试确定拉力F T3的大小和方向。

解 册究対繼*晦矍*曲：/」平衛ii 殳宦廉，交廉”的钓痕力耳欝珊谊寸c 乃向如I 用 b 陌示.収啪杯爺Cy*血平胡那论鬥式⑴* (?)峡立・解紂佔2…已暂 F 兰5 am N .棗与撑祎自虫不计匚求 BC'ffK 内力及铁员 的反力。

解该系统曼力如图(訂， 三力匸交于艰0・苴封訥的力 三角膠如图冷人祥得 屉二5OOON 』仏 二疔000 W2-2在铰链A 、B 处有力F i , F 2作用，如图所示。

该机 F i 与F 2的关系。

2-3铰链4杆机构CABD 的CD 边固定, 构在图示位置平衡，不计杆自重。

求力 30T >◎60°检(b)B解⑴柠点掐坐WAS 力如囲 归所示"H3平祈刖论咼节点瓦腿标歴覺力如国 所小*血丫轉理论得2S -F^ ccs 30fr -f ； cosW ）0 =0^=-^=—^— = 1.553^F 、: - 0.644已扣两伦备車P A ^P L •处于T册状态,杆電不比求I ）若片=丹=巴 角e -?2）若 P A - 300 B = 0血=?ffi 八5两轮受力分别 如图示■对A 辂育SX = 0* F 刚 cEjedO* — F\g oos$ = 0SY 二 0a F sx tin60T - F 屈 sinfl - P A = tj对 B 轮育 SX ■ 0, Fn ooa? - F,\&8^3(/ = 0 IV = 0. F rw sinff 下 F 斶 anJO* - P n =(1) 四牛封程嬴立求AL 爾＜3-30*(2) 把拧-0\F A - 300 M 代入方社，联立解筹P fl = 100 N2-5如图2-10所示，刚架上作用力F 。

试分别计算力F解 M A (F) = -FbcoseM s [F) - -Fb cos0 + FosinB二F(osiii0-bcos0)2-6已知梁AB 上作用1力偶，力偶矩为M ，梁长为I ，梁重不计。

工程力学答案详解1-1试画出以下各题中圆柱或圆盘的受力图。

与其它物体接触处的摩擦力均略去。

解：1-2 试画出以下各题中AB 杆的受力图。

(a) B(b)(c)(d)A(e)A(a)(b) A(c)A(d)A(e)(c)(a)(b)解：1-3 试画出以下各题中AB 梁的受力图。

(d)(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)解：1-4 试画出以下各题中指定物体的受力图。

(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。

解：(a)F (b)W(c)(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BF D1-5 试画出以下各题中指定物体的受力图。

(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。

解：(a)(d) FC(e)WB (f)F FBC(c)(d)AT F BAF (b)(e)(b)(c)(d)(e)CAA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。

解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。

2-3 水平力F 作用在刚架的B 点，如图所示。

如不计刚架重量，试求支座A 和D 处的约束力。

解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。