史密斯预估器

基于积分时滞系统史密斯预估器的研究丁晓迪;崔宝同【摘要】在积分时滞系统(IPDT)中,传统的史密斯预估器不能很好的消除稳态误差,而且在模型失配时易产生欠补偿问题.为此,文中提出了改进型的史密斯预估器,首先利用反馈控制器,将实际过程与模型过程的误差反馈到控制信号端.其次,在控制对象端加上串联控制器和反馈补偿控制器,分别采用不同的方法进行设计,以消除扰动对系统的影响.MATLAB仿真结果显示,系统具有较好的输出响应,能够有效消除扰动误差.%Traditional Smith-Predictor fails to provide a null steady-state error in the presence of a constant load disturbance if the process exhibits an integral dynamics (IPDT), and under compensation when the model mismatches. The modified Smith-Predictor is proposed for it. Firstly, the feedback controller can transmit the error which comes from the difference between actual process and the model process to the control signal. Secondly, series controller and Feedback recourse controller are added to the input of plant, and the controllers are using different methods to design. MATLAB simulation shows that the system has better output response, and also eliminates the steady-state error.【期刊名称】《计算机系统应用》【年(卷),期】2016(025)003【总页数】5页(P262-266)【关键词】积分时滞系统;史密斯预估器;反馈控制器;扰动误差【作者】丁晓迪;崔宝同【作者单位】江南大学物联网工程学院,无锡 214122;江南大学物联网工程学院,无锡 214122【正文语种】中文现代工业生产过程中, 往往存在着时滞环节. 这些滞后时间对于系统的控制性能会产生极为不利的影响. 因此, 如何补偿时滞则显得尤为重要. 针对这一问题, 1957年, Smith OJ[1]提出了传统的史密斯预估器(Smith-predictor). 其工作原理是在系统的反馈回路中引入补偿装置, 将控制通道传递函数中的纯滞后部分与其他部分分离, 因此消除滞后因子带来的影响. 但是传统的史密斯预估器也存在着一些问题: ①控制对象含有纯积分环节时, 无法消除系统的稳态误差; ②系统真实模型与预估模型不匹配时, 传统的史密斯预估器难以适用[2-3].目前, 对于传统的史密斯预估器的改进主要集中在改进史密斯预估器的结构和更新控制器的设计方法. 文献[4~6]添加了反馈控制器和滤波器, 以减弱系统的超调量. 近些年, 在传统的史密斯预估器的基础上结合模糊控制[7], 自适应控制[8], 人工神经网络[9,10], 鲁棒控制[11~13]等算法, 对系统进行改进. 文献[14]针对传统史密斯预估器的稳态误差问题, 将Watanabe法和泰勒公式结合起来, 消除了系统的稳态误差, 但同时忽略了系统的余项因此会产生超调量.通过对史密斯预估器结构的改进形成了Astrom法, Matausek法, Majhi法, Kaya 法, Liu法等. 另外利用鲁棒控制, Mac-PID, 自适应控制算法等对史密斯预估器的控制器进行设计. 但当系统为纯积分时滞系统并且存在外部扰动时, 很难实现消除稳态误差的同时, 克服系统的扰动误差.本文研究的对象是积分时滞系统(IPDT), 并且对传统的史密斯预估器进行了改进, 引进了一个误差反馈控制器,能够及时的把史密斯预估模块和真实模块产生的误差反馈给控制信号, 消除稳态误差, 并且能够快速抑制干扰信号. 此外, 采用标准二阶参数模型法对串联控制器进行设计. 而对于反馈控制器, 由于时滞因子存在于闭环传递函数的分母中, 会导致系统的不稳定, 因此采用改进的Watanabe法对此进行设计, 将反馈控制器设计为一个集成模块, 并选取合适的参数, 有效的克服了时滞因子对系统的影响.1 传统的史密斯预估器传统的史密斯预估器结构如图1所示[1], 图中为控制对象, 为前向控制器, 为时滞因子, R为系统的输入, D为系统的外部扰动, Y为系统的输出.图 1 史密斯预估器结构图基本思想: 通过过程的数学模型以内反馈方式包围常规的控制器, 一般为比例积分(PI), 比例微分(PD), 比例积分微分(PID)形式. 从而使闭环传递函数的特征方程不含纯滞后环节, 消除了时滞的不利影响. 前向控制器的设计方案一般是将史密斯预估器和内模控制器结合起来, 即IMC-Smith.但是, 由传统的史密斯预估器结构可以看出, 对于预估模型和真实模型的参数匹配度要求很高. 因此, 史密斯预估器对于模型的偏差极为敏感, 甚至极小的模型偏差都可能导致闭环系统的不稳定. 此外, 对于积分时滞系统, 传统的史密斯预估器在求解时会存在稳态误差, 因此需要对其进行改进.2 改进的史密斯预估器改进的史密斯预估器的系统结构如图2所示. 与传统的史密斯预估器不同, 系统结构中添加了反馈控制器, 能够对模型失配的误差进行调节. 此外, 整个系统并没有将误差反馈到输入端, 有效避免积分时滞情况下的稳态误差. 另外, 对于反馈控制器采用改进的Watanabe法进行设计, 能够快速的抑制系统的扰动误差, 使系统迅速达到稳定. 其中为真实模型, 为预估模型, 为时滞时间.图 2 改进的史密斯预估器结构图一般情况下, . 取积分时滞系统对象为, 则可以根据结构图求出:(1)(2)即(3)(4)对于前向控制器, 设为PI控制器, 令 , 将其带入传递函数(3)可得:(5)而标准的二阶系统模型方程[15]:(6)可以通过对比, 得到以下公式:(7)(8)对式(7), (8)进行求解, 得到的公式:(9)选取不同的阻尼比(ζ ), 振荡频率 ()值, 比较曲线的上升时间, 超调量.对于扰动误差传递函数, 系统的特征多项式为(10)与传统的史密斯预估器不同, 反馈控制器存在于干扰传递函数中, 并且闭环传递函数分母上含有非最小相位系统, 带有时滞因子, 会导致系统的不稳定. Watanabe[16]在1981年提出了Watanabe法则, 回避了不稳定环节. 但是, 在求解时, 将时滞因子用一阶Pade公式进行了替代, 很明显此方法的缺陷是忽略了泰勒展开式的余项,与真实的系统有较大的偏差. 为了避免这一问题, 文中, 并没有直接求出控制器, 而是设计成一个反馈结构, 再采用改进的Watanabe法进行设计, 设计方法如下, 令 (11)则模块的结构图如图3所示.图3 模块结构图对于系统克服稳态误差的证明如下, 将式(11)带入式(4), 得到公式(12)由式(12)分析出, 将设计成为一个模块的优点是系统的扰动传递函数中不再包含非最小相位系统, 因此稳定性会有所提高, 不会出现很大的超调量, 由此可以对其进行化简, 首先根据文献[16]中的有关参数设置, , , 并且可以使得, 则(13)对于模块的求解, 可以采取反向求解的思路, , 则可以得到:(14)对公式进行化简, 可以得到下列公式(15)(16)根据式(15) , (16)选取模块的函数关系式, 令(17)文中, 对传统的史密斯预估器进行了改进, 改进的史密斯预估器在系统对象为积分时滞系统时, 依旧能够很好的消除系统地稳态误差, 并且抑制系统地干扰信号. 从结构上来看, 添加了反馈控制器, 将其设计为一个更小的模块, 有效地避免了Watanabe法出现的忽略余项问题. 而对于控制器而言, 串联控制器与二阶系统联系了起来, 文中选取了比例积分(PI)控制器, 而没有选取比例微分(PD)或者比例积分微分(PID)控制器, 是由于后两者在仿真上升阶段会出现一定的震荡, 而前者更加平稳, 且上升时间更短. 反馈控制器中关键的是的设计, 根据等价无穷小的原则, 求得具体参数.3 仿真研究文中, 选取工业过程中常见的积分时滞系统, 即, 与文献[5]进行比较, 选取对象参数K=1, τ=1. 由公式(9), 可知前向控制器C(s)与参数阻尼比(ζ), 振荡频率()有关. 分别研究阻尼比和振荡频率发生变化时对系统超调量()和调节时间()产生的影响, 令ζ =10, = 0.1, 1, 5, 则系统产生的响应曲线如图4所示.图4 因子对系统的影响从上图可以看出, 当ζ一定时, 越大, 上升时间越快. 然后令=1, ζ= 1, 5, 10, 则系统产生的相应曲线如图5所示.图5 ζ因子对系统的影响图5表明, 一定时, ζ越大, 上升时间越快, 超调量越小. 选取对象参数K=1, τ=1, 将其带入等式(17)得:(18)根据图4图5, 可以看出, 串联控制器C(s)参数的选择为=1, ζ =10时, 效果最好, 则可知, 与文献[5]仿真结果进行对比, 如图6, 图7所示.图 6 模型失配误差对比图仿真表明: 当系统存在外界扰动, 文献[5]的模型失配误差会产生一定的震荡, 并且逐渐趋于一个稳定值, 但不为零, 因此误差依旧会存在. 而本文的模型失配误差会随着时间的推移而逐渐削减为零, 即控制对象和预估对象会逐渐近似相等.图 7 输出对比图仿真表明: 文献[5]中提出来的针对IPDT对象的史密斯预估器, 上升时间为3.4s. 在有扰动的情况下, 伴随着一定的震荡, 超调量6%左右, 调节时间为35s. 而文中提出的设计方案, 上升时间短, 接近1s, 几乎没有超调, 调节时间更短, 约为28s, 整体性能都比文献[8]好.4 结语文中以IPDT时滞系统为研究对象, 分析了传统的史密斯预估器的问题, 并且针对稳态误差和稳定性两个问题进行了讨论, 提出了改进的史密斯预估器. 首先添加反馈控制器, 将误差信号送至控制端, 使得该系统能够较好的跟踪输入信号, 克服扰动信号的干扰. 并且分别采用二阶模型参数法和改进的Watanabe法对串联控制器, 反馈控制器进行了设计, 系统仿真结果表明:经过改进后的史密斯预估器, 稳态误差为零, 调节时间短, 超调量小, 具有很好的稳定性和抗干扰能力.参考文献1 Smith OJ. Closer control of loops with dead time. Chemistry Engineering Progress, 1957, 53(5): 217–219.2 Saravana KG, Wahidbanu RS, Arun KG. Performance analysis of modified Smith predictor for integrating and time-delay processes. Indian Chemical Engineer, 2011, 53(4): 261–270.3 Franco B, Daniele C, Stefano M. Stable LPV realisation of the Smith predictor. International Journal of Systems Science, 2015, 46(12): 1–9.4 Zheng D, Fang JA, Ren ZY. Modified Smith predictor for frequency identification and disturbance rejection of single signal. ISA Trans., 2010, 49(1): 95–105.5 Chien L, Paulo H. Design the remote control system with the time-delay estimator and the adaptive Smith predictor. IEEE Trans. on industrial informatics, 2010, 6(1): 73–80.6 Julio EN, Rafael S, Massimiliano V, et al. An automatic tuningmethodology for a unified dead-time compensator. Control Engineering Practice, 2014, 27: 11–22.7 安连祥,马华民,刘永刚,刘新艳.基于改进Smith预估器的二阶时滞系统.计算机仿真,2011,28(1):198–233.8 Yildiray Y, Anuradha A, Iiyav K. Adaptive posicast controller for time-delay systems with relative degree n<2. Automatica, 2010, 46(2): 279–289.9 Tsai MH, Tung PC. A robust disturbance reduction scheme for linear small delay systems with unknown frequencies. ISA Trans., 2012, 51(3): 362–372.10 Lin e, Zhou W, Li C. Simulink simulation of single neuron PID and smith predictive control based on the s function. 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control. 2013. 1548–1551.11 Ibrahim K. IMC based automatic tuning method for PID controllers in a Smith predictor configuration. Computers and Chemical Engineering, 2004, 28(3): 281–290.12 Luca DC, Saverio M, Silviu IN. Robust stability analysis of Smith predictor-based congestion control algorithms for computer networks. Automatica, 2011, 47(8): 1685–1692.13 Campos D, Luna RJ. Performance study of distributed power control algorithm under time delay and measurement uncertainty. IEEE America Trans., 2013, 11(2): 690–697.14 Modirnia R, Boulet B. Application of the Watanabe Modified Smith predictor technique in thermoforming.2012 American Control ConferenceCanada, 2012:6448– 6454.15 黄灿,桂卫华,阳春华,蒋朝辉,谢永芳.多变量时滞过程解耦Smith控制.控制理论与应用,2010,27(10):1393–1398.16 Watanabe K, Ito M. A process-model control for linear systems with delay. IEEE Trans. on Automatic Control, 1981, 26(6): 1261–1269. Improved Smith-Predictors Based on IPDT SystemsDING Xiao-Di, CUI Bao-Tong(School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China)Abstract：Traditional Smith-Predictor fails to provide a null steady-state error in the presence of a constant load disturbance if the process exhibits an integral dynamics (IPDT), and under compensation when the model mismatches. The modified Smith-Predictor is proposed for it. Firstly, the feedback controller can transmit the error which comes from the difference between actual process and the model process to the control signal. Secondly, series controller and Feedback recourse controller are added to the input of plant, and the controllers are using different methods to design. MATLAB simulation shows that the system has better output response, and also eliminates the steady-state error.Key words： IPDT; Smith-predictor; feedback controller; disturbance error ①基金项目：高等学校学科创新资助(B12018)收稿时间：2015-06-25;收到修改稿时间:2015-09-06传统的史密斯预估器结构如图1所示[1], 图中为控制对象, 为前向控制器, 为时滞因子, R为系统的输入, D为系统的外部扰动, Y为系统的输出.基本思想: 通过过程的数学模型以内反馈方式包围常规的控制器, 一般为比例积分(PI), 比例微分(PD), 比例积分微分(PID)形式. 从而使闭环传递函数的特征方程不含纯滞后环节, 消除了时滞的不利影响. 前向控制器的设计方案一般是将史密斯预估器和内模控制器结合起来, 即IMC-Smith.但是, 由传统的史密斯预估器结构可以看出, 对于预估模型和真实模型的参数匹配度要求很高. 因此, 史密斯预估器对于模型的偏差极为敏感, 甚至极小的模型偏差都可能导致闭环系统的不稳定. 此外, 对于积分时滞系统, 传统的史密斯预估器在求解时会存在稳态误差, 因此需要对其进行改进.2 改进的史密斯预估器改进的史密斯预估器的系统结构如图2所示. 与传统的史密斯预估器不同, 系统结构中添加了反馈控制器, 能够对模型失配的误差进行调节. 此外, 整个系统并没有将误差反馈到输入端, 有效避免积分时滞情况下的稳态误差. 另外, 对于反馈控制器采用改进的Watanabe法进行设计, 能够快速的抑制系统的扰动误差, 使系统迅速达到稳定. 其中为真实模型, 为预估模型, 为时滞时间.图 2 改进的史密斯预估器结构图一般情况下, . 取积分时滞系统对象为, 则可以根据结构图求出:(1)(2)即(3)(4)对于前向控制器, 设为PI控制器, 令 , 将其带入传递函数(3)可得:(5)而标准的二阶系统模型方程[15]:(6)可以通过对比, 得到以下公式:(7)(8)对式(7), (8)进行求解, 得到的公式:(9)选取不同的阻尼比(ζ ), 振荡频率 ()值, 比较曲线的上升时间, 超调量.对于扰动误差传递函数, 系统的特征多项式为(10)与传统的史密斯预估器不同, 反馈控制器存在于干扰传递函数中, 并且闭环传递函数分母上含有非最小相位系统, 带有时滞因子, 会导致系统的不稳定. Watanabe[16]在1981年提出了Watanabe法则, 回避了不稳定环节. 但是, 在求解时, 将时滞因子用一阶Pade公式进行了替代, 很明显此方法的缺陷是忽略了泰勒展开式的余项, 与真实的系统有较大的偏差. 为了避免这一问题, 文中, 并没有直接求出控制器, 而是设计成一个反馈结构, 再采用改进的Watanabe法进行设计, 设计方法如下, 令 (11)则模块的结构图如图3所示.图3 模块结构图对于系统克服稳态误差的证明如下, 将式(11)带入式(4), 得到公式(12)由式(12)分析出, 将设计成为一个模块的优点是系统的扰动传递函数中不再包含非最小相位系统, 因此稳定性会有所提高, 不会出现很大的超调量, 由此可以对其进行化简, 首先根据文献[16]中的有关参数设置, , , 并且可以使得, 则(13)对于模块的求解, 可以采取反向求解的思路, , 则可以得到:(14)对公式进行化简, 可以得到下列公式(15)(16)根据式(15) , (16)选取模块的函数关系式, 令(17)文中, 对传统的史密斯预估器进行了改进, 改进的史密斯预估器在系统对象为积分时滞系统时, 依旧能够很好的消除系统地稳态误差, 并且抑制系统地干扰信号. 从结构上来看, 添加了反馈控制器, 将其设计为一个更小的模块, 有效地避免了Watanabe法出现的忽略余项问题. 而对于控制器而言, 串联控制器与二阶系统联系了起来, 文中选取了比例积分(PI)控制器, 而没有选取比例微分(PD)或者比例积分微分(PID)控制器, 是由于后两者在仿真上升阶段会出现一定的震荡, 而前者更加平稳, 且上升时间更短. 反馈控制器中关键的是的设计, 根据等价无穷小的原则, 求得具体参数.3 仿真研究文中, 选取工业过程中常见的积分时滞系统, 即, 与文献[5]进行比较, 选取对象参数K=1, τ=1. 由公式(9), 可知前向控制器C(s)与参数阻尼比(ζ), 振荡频率()有关. 分别研究阻尼比和振荡频率发生变化时对系统超调量()和调节时间()产生的影响, 令ζ =10, = 0.1, 1, 5, 则系统产生的响应曲线如图4所示.图4 因子对系统的影响从上图可以看出, 当ζ一定时, 越大, 上升时间越快. 然后令=1, ζ= 1, 5, 10, 则系统产生的相应曲线如图5所示.图5 ζ因子对系统的影响图5表明, 一定时, ζ越大, 上升时间越快, 超调量越小. 选取对象参数K=1, τ=1, 将其带入等式(17)得:(18)根据图4图5, 可以看出, 串联控制器C(s)参数的选择为=1, ζ =10时, 效果最好, 则可知, 与文献[5]仿真结果进行对比, 如图6, 图7所示.图 6 模型失配误差对比图仿真表明: 当系统存在外界扰动, 文献[5]的模型失配误差会产生一定的震荡, 并且逐渐趋于一个稳定值, 但不为零, 因此误差依旧会存在. 而本文的模型失配误差会随着时间的推移而逐渐削减为零, 即控制对象和预估对象会逐渐近似相等.图 7 输出对比图仿真表明: 文献[5]中提出来的针对IPDT对象的史密斯预估器, 上升时间为3.4s. 在有扰动的情况下, 伴随着一定的震荡, 超调量6%左右, 调节时间为35s. 而文中提出的设计方案, 上升时间短, 接近1s, 几乎没有超调, 调节时间更短, 约为28s, 整体性能都比文献[8]好.4 结语文中以IPDT时滞系统为研究对象, 分析了传统的史密斯预估器的问题, 并且针对稳态误差和稳定性两个问题进行了讨论, 提出了改进的史密斯预估器. 首先添加反馈控制器, 将误差信号送至控制端, 使得该系统能够较好的跟踪输入信号, 克服扰动信号的干扰. 并且分别采用二阶模型参数法和改进的Watanabe法对串联控制器, 反馈控制器进行了设计, 系统仿真结果表明:经过改进后的史密斯预估器, 稳态误差为零, 调节时间短, 超调量小, 具有很好的稳定性和抗干扰能力.参考文献1 Smith OJ. Closer control of loops with dead time. Chemistry Engineering Progress, 1957, 53(5): 217–219.2 Saravana KG, Wahidbanu RS, Arun KG. Performance analysis of modified Smith predictor for integrating and time-delay processes. Indian Chemical Engineer, 2011, 53(4): 261–270.3 Franco B, Daniele C, Stefano M. Stable LPV realisation of the Smith predictor. International Journal of Systems Science, 2015, 46(12): 1–9.4 Zheng D, Fang JA, Ren ZY. Modified Smith predictor for frequency identification and disturbance rejection of single signal. ISA Trans., 2010, 49(1): 95–105.5 Chien L, Paulo H. Design the remote control system with the time-delay estimator and the adaptive Smith predictor. IEEE Trans. on industrial informatics, 2010, 6(1): 73–80.6 Julio EN, Rafael S, Massimiliano V, et al. An automatic tuning methodology for a unified dead-time compensator. Control Engineering Practice, 2014, 27: 11–22.7 安连祥,马华民,刘永刚,刘新艳.基于改进Smith预估器的二阶时滞系统.计算机仿真,2011,28(1):198–233.8 Yildiray Y, Anuradha A, Iiyav K. Adaptive posicast controller for time-delay systems with relative degree n<2. Automatica, 2010, 46(2): 279–289.9 Tsai MH, Tung PC. A robust disturbance reduction scheme for linear small delay systems with unknown frequencies. ISA Trans., 2012, 51(3): 362–372.10 Lin e, Zhou W, Li C. Simulink simulation of single neuron PID and smith predictive control based on the s function. 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control. 2013. 1548–1551.11 Ibrahim K. IMC based automatic tuning method for PID controllers in a Smith predictor configuration. Computers and Chemical Engineering, 2004, 28(3): 281–290.12 Luca DC, Saverio M, Silviu IN. Robust stability analysis of Smith predictor-based congestion control algorithms for computer networks. Automatica, 2011, 47(8): 1685–1692.13 Campos D, Luna RJ. Performance study of distributed power control algorithm under time delay and measurement uncertainty. IEEE America Trans., 2013, 11(2): 690–697.14 Modirnia R, Boulet B. Application of the Watanabe Modified Smith predictor technique in thermoforming.2012 American Control Conference Canada, 2012:6448– 6454.15 黄灿,桂卫华,阳春华,蒋朝辉,谢永芳.多变量时滞过程解耦Smith控制.控制理论与应用,2010,27(10):1393–1398.16 Watanabe K, Ito M. A process-model control for linear systems with delay. IEEE Trans. on Automatic Control, 1981, 26(6): 1261–1269. Improved Smith-Predictors Based on IPDT SystemsDING Xiao-Di, CUI Bao-Tong(School of Internet of Things Engineering, Jiangnan University, Wuxi 214122, China)Abstract：Traditional Smith-Predictor fails to provide a null steady-state error in the presence of a constant load disturbance if the process exhibits an integral dynamics (IPDT), and under compensation when the model mismatches. The modified Smith-Predictor is proposed for it. Firstly, the feedback controller can transmit the error which comes from the difference between actual process and the model process to the control signal. Secondly, series controller and Feedback recourse controller are added to the input of plant, and the controllers are using different methods to design. MATLAB simulation shows that the system has better output response, and also eliminates the steady-state error.Key words： IPDT; Smith-predictor; feedback controller; disturbance error ①基金项目：高等学校学科创新资助(B12018)收稿时间：2015-06-25;收到修改稿时间:2015-09-06基本思想: 通过过程的数学模型以内反馈方式包围常规的控制器, 一般为比例积分(PI), 比例微分(PD), 比例积分微分(PID)形式. 从而使闭环传递函数的特征方程不含纯滞后环节, 消除了时滞的不利影响. 前向控制器的设计方案一般是将史密斯预估器和内模控制器结合起来, 即IMC-Smith.但是, 由传统的史密斯预估器结构可以看出, 对于预估模型和真实模型的参数匹配度要求很高. 因此, 史密斯预估器对于模型的偏差极为敏感, 甚至极小的模型偏差都可能导致闭环系统的不稳定. 此外, 对于积分时滞系统, 传统的史密斯预估器在求解时会存在稳态误差, 因此需要对其进行改进.改进的史密斯预估器的系统结构如图2所示. 与传统的史密斯预估器不同, 系统结构中添加了反馈控制器, 能够对模型失配的误差进行调节. 此外, 整个系统并没有将误差反馈到输入端, 有效避免积分时滞情况下的稳态误差. 另外, 对于反馈控制器采用改进的Watanabe法进行设计, 能够快速的抑制系统的扰动误差, 使系统迅速达到稳定. 其中为真实模型, 为预估模型, 为时滞时间.一般情况下, . 取积分时滞系统对象为, 则可以根据结构图求出:即对于前向控制器, 设为PI控制器, 令 , 将其带入传递函数(3)可得:而标准的二阶系统模型方程[15]:可以通过对比, 得到以下公式:对式(7), (8)进行求解, 得到的公式:选取不同的阻尼比(ζ ), 振荡频率 ()值, 比较曲线的上升时间, 超调量.对于扰动误差传递函数, 系统的特征多项式为与传统的史密斯预估器不同, 反馈控制器存在于干扰传递函数中, 并且闭环传递函数分母上含有非最小相位系统, 带有时滞因子, 会导致系统的不稳定. Watanabe[16]在1981年提出了Watanabe法则, 回避了不稳定环节. 但是, 在求解时, 将时滞因子用一阶Pade公式进行了替代, 很明显此方法的缺陷是忽略了泰勒展开式的余项, 与真实的系统有较大的偏差. 为了避免这一问题, 文中, 并没有直接求出控制器, 而是设计成一个反馈结构, 再采用改进的Watanabe法进行设计, 设计方法如下, 令则模块的结构图如图3所示.对于系统克服稳态误差的证明如下, 将式(11)带入式(4), 得到公式(12)由式(12)分析出, 将设计成为一个模块的优点是系统的扰动传递函数中不再包含非最小相位系统, 因此稳定性会有所提高, 不会出现很大的超调量, 由此可以对其进行化简, 首先根据文献[16]中的有关参数设置, , , 并且可以使得, 则(13)对于模块的求解, 可以采取反向求解的思路, , 则可以得到:(14)对公式进行化简, 可以得到下列公式(15)(16)根据式(15) , (16)选取模块的函数关系式, 令(17)文中, 对传统的史密斯预估器进行了改进, 改进的史密斯预估器在系统对象为积分时滞系统时, 依旧能够很好的消除系统地稳态误差, 并且抑制系统地干扰信号. 从结构上来看, 添加了反馈控制器, 将其设计为一个更小的模块, 有效地避免了Watanabe法出现的忽略余项问题. 而对于控制器而言, 串联控制器与二阶系统联系了起来, 文中选取了比例积分(PI)控制器, 而没有选取比例微分(PD)或者比例积分微分(PID)控制器, 是由于后两者在仿真上升阶段会出现一定的震荡, 而前者更加平稳, 且上升时间更短. 反馈控制器中关键的是的设计, 根据等价无穷小的原则, 求得具体参数.3 仿真研究文中, 选取工业过程中常见的积分时滞系统, 即, 与文献[5]进行比较, 选取对象参数K=1, τ=1. 由公式(9), 可知前向控制器C(s)与参数阻尼比(ζ), 振荡频率()有关. 分别研究阻尼比和振荡频率发生变化时对系统超调量()和调节时间()产生的影响, 令ζ =10, = 0.1, 1, 5, 则系统产生的响应曲线如图4所示.图4 因子对系统的影响从上图可以看出, 当ζ一定时, 越大, 上升时间越快. 然后令=1, ζ= 1, 5, 10, 则系统产生的相应曲线如图5所示.图5 ζ因子对系统的影响图5表明, 一定时, ζ越大, 上升时间越快, 超调量越小. 选取对象参数K=1, τ=1, 将其带入等式(17)得:(18)根据图4图5, 可以看出, 串联控制器C(s)参数的选择为=1, ζ =10时, 效果最好, 则可知, 与文献[5]仿真结果进行对比, 如图6, 图7所示.图 6 模型失配误差对比图仿真表明: 当系统存在外界扰动, 文献[5]的模型失配误差会产生一定的震荡, 并且逐渐趋于一个稳定值, 但不为零, 因此误差依旧会存在. 而本文的模型失配误差会随着时间的推移而逐渐削减为零, 即控制对象和预估对象会逐渐近似相等.图 7 输出对比图仿真表明: 文献[5]中提出来的针对IPDT对象的史密斯预估器, 上升时间为3.4s. 在有扰动的情况下, 伴随着一定的震荡, 超调量6%左右, 调节时间为35s. 而文中提出的设计方案, 上升时间短, 接近1s, 几乎没有超调, 调节时间更短, 约为28s, 整体性能都比文献[8]好.4 结语文中以IPDT时滞系统为研究对象, 分析了传统的史密斯预估器的问题, 并且针对稳态误差和稳定性两个问题进行了讨论, 提出了改进的史密斯预估器. 首先添加反馈控制器, 将误差信号送至控制端, 使得该系统能够较好的跟踪输入信号, 克服扰动信号的干扰. 并且分别采用二阶模型参数法和改进的Watanabe法对串联控制器, 反馈控制器进行了设计, 系统仿真结果表明:经过改进后的史密斯预估器, 稳态误差为零, 调节时间短, 超调量小, 具有很好的稳定性和抗干扰能力.参考文献1 Smith OJ. Closer control of loops with dead time. Chemistry Engineering。

施密斯预估控制姓名：学号：班级：1 实验目的对大多数控制系统，采用常规的控制技术均可以达到满意的控制效果，但对于复杂及特殊要求的控制系统，采用常规的控制室技术很难达到目的，在这种情况下，就需要采用复杂控制技术，其中Smith 预估控制算法是常用的一种，通过本实验加深对Smith 预估控制算法的理解和掌握。

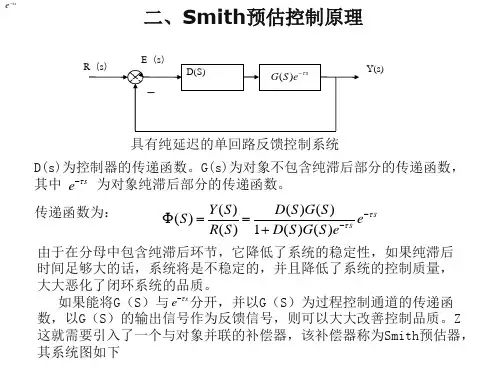
2 实验原理图1为被控对象具有纯滞后特性的单回路反馈控制系统，D （s ）是控制器，被控对象的传递函数为etss -)(G p ，其中，)(G p s 为被控对象中不包含纯滞后部分的传递函数，ts-e为被控对象纯滞后部分的传递函数。

)(t r )(t e )(t u )(t y_施密斯预估原理：与D （s ）并接一补偿环节，用来补偿被控对象中的纯滞后部分，这个补偿环节称为预估器，其传递函数为)1)((G p tse s --，t 为纯滞后时间，补偿后的系统结构如图2所示。

)(t r )(t e )(t u )(t y_ _)(t y τ由施密斯预估控制器)1)((G p tses --和控制器D （s ）组成的回路陈伟纯滞后补偿器，)(s Ds e s τ-)(G p)(s Ds e s τ-)(G p)1)((G p ts e s --其传递函数为：)1)(()(1)()(D m s p e s G s D s D s τ--+=经过补偿后的系统闭环传递函数为：s p p sp m sp m e s G s D s G s D es G s D e s G s D τττ---+=+=Φ)()(1)()()()(1)()(s ）（该式说明，进过补偿后，消除了之后部分对控制系统的影响，因为式中ts-e 在闭环控制回路之外，不影响系统的稳定性。

设广义被控对象为：1011()()()1Ts s se e H s G s G s es T sττ----==⋅+取T=1、τ=2、T 1=2.88，经采样（T=1s ）保持后，其广义对象z 传递函数为00.2934()0.7066G z z =-，而2se -转换为2个单位迟延。

第五节 Smith 预估控制Smith 预估控制方法是在1957年由Smith 提出来的，其特点是预先估计被控系统在基本扰动下的动态特性，然后用预估器进行补偿，力图使被延迟的被控制量超前反映到控制器中，使控制器提前动作，从而显著地减小系统的超调量，同时加速系统的调节过程。

一、Smith 预估控制原理预估控制系统原理图如图7-24所示。

(a) 预估控制系统原理框图 (b) Smith 预估器图7-24 预估控制系统原理图 图中，s e s G τ−)(p 为具有时滞为τ的对象传递函数，其中)(p s G 为被控对象；)(m s G 为内部模型（又称为对象的标称或名义模型），即Smith 预估器的传递函数，()s e s G s G τ−−=1)()(p m ；)(s D 为（前馈）内模控制器；)(s d 为扰动；)(s R 为参考输入；)(s Y 为被控对象输出；)(m s Y 为内部模型输出。

由图7-24可知，将Smith 预估器与控制器（或被控对象）二者并联。

在理论上可以使被控对象的时间滞后得到完全补偿，控制器的设计就不必再考虑对象的时滞作用了。

现在，系统中假设没有补偿器（预估器），则控制器输出与被控量之间的传递函数便为 s e s G s U s Y τ−=)()()(p (7-50) 上式表明，受到)(s U 控制作用的被控量)(s Y 要经过纯滞后时间τ之后才能反馈到系统控制器输入端。

若采用预估补偿器，则控制量)(s U 与反馈到控制器输入端的反馈信号)(s Y ′之间的传递函数乃是两个并联通道之和，即)()()()(m p s G e s G s U s Y s +=′−τ (7-51) 为使反馈信号)(s Y ′不发生时间滞后τ，则要求(7-51)式满足)()())(()()(p m p s G s G e s s G s U s Y s =+=′−τ (7-52) 于是，就导出了Smith 预估补偿器的传递函数为()s e s G s G τ−−=1)()(p m (7-53) 在系统中设置了Smith 预估器的情况下，可以推导出系统的闭环传递函数为)()(1)()()1)(()(1)()(1)1)(()(1)()()()(p p p p p p s G s D e s G s D e s G s D e s G s D e s G s D e s G s D s R s Y s s s s+=−++−+=−−−−−ττττ (7-54) 由上式可以明显看出，在系统的特征方程中，已经不含有s e τ−项。

东南大学能源与环境学院实验报告课程名称：实验名称：院（系）：专业：姓名：杨康学号：实验室：实验组别：同组人员：实验时间：年月日评定成绩：审阅教师：目录一．实验目的 (3)二．实验内容 (3)三．实验步骤 (3)四．实验分析 (12)实验二 Smith预估控制实验指导书一实验目的通过实验掌握Smith预估控制的方法及程序编制及调试。

二实验内容１．Smith预估控制系统如图所示，图一对象G(S)= K·e-τs / (1+TS),K = 1, T1 = 10 s , τ = 5 s ,1Wc(z)采用数字PI控制规律。

２．对象扰动实验画出U(t) = u0·1(t)时，y(t)曲线。

３．Smith预估控制(1)构造Wτ(S)，求出Wτ(Z)。

(2)整定Wc(s)(按什么整定？)(3)按图仿真，并打印曲线。

（4）改变Wτ(S)中K，τ（对象不变），进行仿真比较，观察它们对调节过程的影响。

三实验步骤1、对象扰动实验（1）差分方程如附录。

（2）源程序如下：#include"iostream.h"#include"math.h"#include"fstream.h"void main(){fstream outfile("data1.xls",ios::out);double t;double u0;cout<<"请输入采样周期:";cin>>t;cout<<"请输入阶跃幅值:";cin>>u0;double ee=pow(2.718,(-t/10.0));int N;int i;double u[100],y[100];for(i=0;i<100;i++){u[i]=u0;y[i]=0.0;}N=1+5/t;for(i=N;i<100;i++){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}for(i=0;i*t<100;i++){cout<<y[i]<<'\t';}for(i=0;i*t<100;i++){outfile<<i*t<<'\t';}outfile<<'\n';for(i=0;i*t<100;i++){outfile<<y[i]<<'\t';}outfile.close();}（3）输出结果：当采样周期T=1，阶跃幅值为1时：Y（t）输出数据：0 0 0 0 0 0 0.0951532 0.181252 0.259159 0.3296520.393438 0.451154 0.503379 0.550634 0.593392 0.6320820.667091 0.698768 0.727431 0.753367 0.776835 0.798070.817284 0.83467 0.850402 0.864637 0.877517 0.8891720.899717 0.909259 0.917894 0.925706 0.932776 0.9391720.94496 0.950197 0.954936 0.959224 0.963104 0.9666150.969792 0.972666 0.975267 0.97762 0.97975 0.9816770.98342 0.984998 0.986425 0.987717 0.988886 0.9899430.9909 0.991766 0.99255 0.993259 0.9939 0.99448 0.9950060.995481 0.995911 0.9963 0.996652 0.996971 0.9972590.99752 0.997756 0.997969 0.998162 0.998337 0.9984960.998639 0.998768 0.998885 0.998991 0.999087 0.9991740.999253 0.999324 0.999388 0.999446 0.999499 0.9995470.99959 0.999629 0.999664 0.999696 0.999725 0.9997510.999775 0.999796 0.999816 0.999833 0.999849 0.9998630.999876 0.999888 0.999899 0.999908 0.999917阶跃响应曲线如下：图二2、Smith预估控制（1）差分方程见附录：（2）源程序如下：#include"iostream.h"#include"math.h"#include"fstream.h"void main(){fstream outfile("data1.xls",ios::out);double t,kp,ki;int t1,k;cout<<"请输入Wt(s)中的K:";cin>>k;cout<<"请输入Wt(s)中的迟延时间t:";cin>>t1;cout<<"请输入采样周期:";cin>>t;cout<<"请输入PI调节器的参数kp:";cin>>kp;cout<<"请输入PI调节器的参数ki:";cin>>ki;double ee=pow(2.718,(-t/10.0));int N,N1;int i;double r[100],e1[100],e2[100],cm[100],q[100],u[100],y[100];for(i=0;i<100;i++){r[i]=1.0;e1[i]=0.0;e2[i]=0.0;u[i]=0.0;y[i]=0.0;cm[i]=0.0;q[i]=0.0;}N=1+5/t;N1=t1/t;cout<<N<<'\t'<<N1<<endl;for(i=0;i<100;i++){if(i==0){e1[i]=r[i];cm[i]=0;q[i]=0;e2[i]=e1[i]-q[i];u[i]=kp*e2[i]+ki*e2[i];}if(i>0&&i<N1){e1[i]=r[i]-y[i-1];cm[i]=ee*cm[i-1]+k*(1-ee)*u[i-1];q[i]=cm[i];e2[i]=e1[i]-q[i];u[i]=u[i-1]+kp*(e2[i]-e2[i-1])+ki*e2[i];if(i>=N){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}}if(i>=N1){e1[i]=r[i]-y[i-1];cm[i]=ee*cm[i-1]+k*(1-ee)*u[i-1];q[i]=cm[i]-cm[i-N1];e2[i]=e1[i]-q[i];u[i]=u[i-1]+kp*(e2[i]-e2[i-1])+ki*e2[i];if(i>=N){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}}}for(i=0;i*t<100;i++){cout<<y[i]<<'\t';}for(i=0;i*t<100;i++){outfile<<i*t<<'\t';}outfile<<'\n';for(i=0;i*t<100;i++){outfile<<y[i]<<'\t';}outfile.close();}（3）输出结果：以下所涉及到的采样周期均为T=1，PI控制器的参数均为Kp=1，Ki=1；当Smith预估器中的K=1，延迟时间τ=5时（即与对象的特性完全符合）：Y（t）输出数据：0 0 0 0 0 0 0.190306 0.421441 0.663641 0.8917551.08676 1.23639 1.37128 1.47104 1.5311 1.549551.52761 1.46956 1.38931 1.29344 1.18983 1.085670.987246 0.89981 0.828799 0.776983 0.745653 0.7345240.741955 0.765251 0.801257 0.846217 0.896223 0.947450.996402 1.04011 1.07631 1.1035 1.1209 1.12848 1.126831.11708 1.10079 1.07973 1.05581 1.03093 1.00680.984919 0.966463 0.952253 0.942744 0.938032 0.937890.941816 0.949101 0.958895 0.970279 0.982333 0.9941951.00511 1.01448 1.02186 1.02698 1.02978 1.030321.02882 1.02561 1.02108 1.01569 1.00987 1.004060.998627 0.993893 0.990086 0.98735 0.985745 0.9852490.985771 0.987163 0.989238 0.991783 0.994581 0.997421.00011 1.0025 1.00445 1.0059 1.0068 1.00715 1.0071.00641 1.00547 1.00428 1.00293 1.00155 1.000220.999027 0.998028 0.997269 0.996773扰动曲线如下：图三当Smith预估器中的K=1，延迟时间τ=2时（即与对象的特性不完全符合）：Y（t）输出数据如下：0 0 0 0 0 0 0.190306 0.421441 0.663641 0.9279711.21095 1.50619 1.810532.08577 2.31463 2.489892.60123 2.63889 2.59562 2.46564 2.25095 1.958931.59989 1.18774 0.740093 0.277571 -0.176632 -0.598368-0.963966 -1.25121 -1.44044 -1.51579 -1.4662 -1.28642-0.977633 -0.547714 -0.0112532 0.610765 1.29164 1.999962.700933.358 3.934554.39588 4.71103 4.854644.80862 4.56351 4.11952 3.48712 2.68715 1.750360.716479 -0.367272 -1.44817 -2.47036 -3.37751 -4.11571-4.63639 -4.89916 -4.87439 -4.54543 -3.91026 -2.98249-1.79168 -0.38278 1.18524 2.8415 4.5062 6.09408 7.518558.69603 9.55045 10.0176 10.0494 9.61689 8.713477.35632 5.58704 3.47109 1.09587 -1.43244 -3.99312-6.45626 -8.68888 -10.5616 -11.9554 -12.7687 -12.9234-12.3704 -11.0941 -9.11507 -6.49149 -3.31832 0.2752394.13026 8.06445 11.88 15.3731 18.3435扰动曲线如下：图四当Smith预估器中的K=2，延迟时间τ=2时（即与对象的特性不完全符合）：Y（t）输出数据如下：0 0 0 0 0 0 0.190306 0.385225 0.546344 0.7250840.920371 1.11455 1.30834 1.46909 1.59338 1.692661.7608 1.79027 1.78227 1.73766 1.66147 1.560211.43778 1.29949 1.15302 1.00558 0.863901 0.7341210.621319 0.529913 0.463425 0.423874 0.411896 0.4269230.467201 0.529943 0.611457 0.707298 0.812552 0.9221031.03084 1.13389 1.22683 1.30585 1.36793 1.410941.4337 1.43598 1.41848 1.38278 1.33121 1.266721.19274 1.11298 1.03127 0.951381 0.876845 0.8108160.75594 0.714253 0.687116 0.675179 0.67838 0.6959770.726605 0.768367 0.818936 0.875681 0.935797 0.9964341.05484 1.10845 1.15505 1.19281 1.22037 1.236891.24206 1.23609 1.21971 1.19405 1.16064 1.12131.07804 1.03296 0.988182 0.945705 0.907359 0.8747110.849012 0.831146 0.82161 0.820506 0.82755 0.8421020.863208 0.889656 0.920041 0.952835 0.986462 1.01937扰动曲线如下：图五四实验分析当系统是特征方程中含有纯迟延项的时候，系统的闭环稳定性事下降的，当迟延时间τ比较大的时候，系统就会不稳定。

基于Simulink的时滞过程Smith 预估控制与IMC控制方法研究Smith预估控制一、基本原理PID控制器因算法简单、鲁棒性好、可靠性高，一直是工业生产过程中应用最广的控制器。

然而实际生产过程往往具有非线性、时变不确定性，应用常规PID控制不能达到理想的控制效果。

这时往往不得不采用模型预测控制、自适应控制等先进控制策略来获得更好的控制性能。

近年来越来越多的研究人员就上层采用模型预测控制这类先进的控制算法，而底层保留传统的PID控制算法，即所谓的预测PID 控制算法，展开了一系列的研究。

1、纯滞后产生的主要原因：1）物料及能量在管道或者容器中传输及运送需要时间；2）物质反应、能量的释放及能量交换需要一定过程和时间；3）设备和设备之间的串联需要许多的中间环节；4）测量装置的响应时间；5）执行机构的动作时间；在控制对象调节通道、测量装置及执行机构等环节存在纯滞后时，控制系统闭环特征方程中就存在纯滞后因子，而且存在纯滞后的环节较多时,系统滞后时间也将随之增加。

因此明显降低了系统的稳定性，而且纯滞后时间越长，系统稳定性就越差。

由于纯滞后的存在，调节作用不及时，导致被调节系统的动态品质下降。

纯滞后越大，则系统的动态品质越差。

2、史密斯预估器原理在单回路控制系统中，控制器的传递函数为GC(s)，被控对象传递函数为G O(s)e-ts，被控对象中不包含纯滞后部分的传递函数为G O(s)，被控对象纯滞后部分的传递函数为e-ts。

则系统的闭环传递函数为Φ(S)=[GC(S)GO(S)e-τs]/[1+GC(S)GO(S)] (1)由式(1)可以看出，系统特征方程中含有纯滞后环节，它会降低系统的稳定性。

史密斯补偿的原理是：与控制器Gc(s)并接一个补偿环节，用来补偿被控对象中的纯滞后部分，这个补偿环节传递函数为Gm(s)=G o(s)(1-e-ts)，t为纯滞后时间，补偿后的系统如图1所示。

图1 史密斯补偿后的控制系统从图中可以看出，若无系统延时时，系统等同于简单的预测PID 控制回路；而当系统有延时时，延时对系统的影响即可由Smith预估控制器消除，而预测PID参数则仅需根据无延时模型来整定，这样就可以避免延时带来的参数整定误差。

史密斯(Smith)预估器工业生产过程中的大多数被控对象都具有较大的纯滞后性质。

被控对象的这种纯滞后性质经常引起超调和持续的振荡。

在20世纪50年代，国外就对工业生产过程中纯滞后现象进行了深入的研究，史密斯提出了一种纯滞后补偿模型，由于当时模拟仪表不能实现这种补偿，致使这种方法在工业实际中无法实现。

随着计算机技术的飞速发展，现在人们可以利用计算机方便地实现纯滞后补偿。

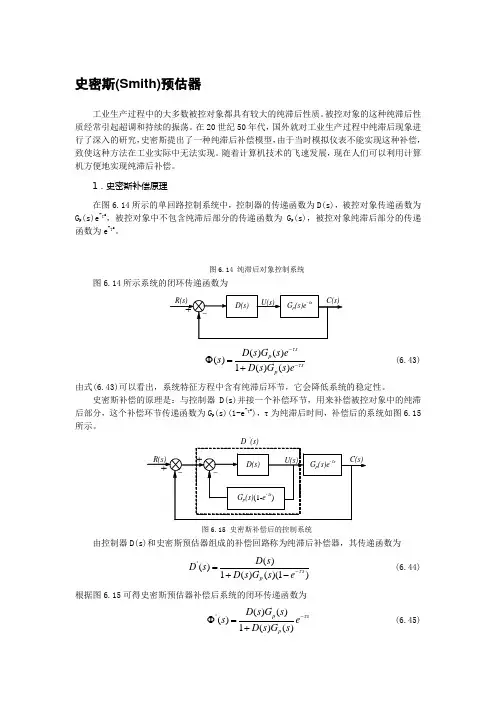
1．史密斯补偿原理在图6.14所示的单回路控制系统中，控制器的传递函数为D(s)，被控对象传递函数为G p (s)e -τs ，被控对象中不包含纯滞后部分的传递函数为G p (s)，被控对象纯滞后部分的传递函数为e -τs 。

图6.14 纯滞后对象控制系统图6.14所示系统的闭环传递函数为()()()1()()sp s p D s G s e s D s G s e ττ--Φ=+ (6.43)由式(6.43)可以看出，系统特征方程中含有纯滞后环节，它会降低系统的稳定性。

史密斯补偿的原理是：与控制器D(s)并接一个补偿环节，用来补偿被控对象中的纯滞后部分，这个补偿环节传递函数为G p (s)(1-e -τs )，τ为纯滞后时间，补偿后的系统如图6.15所示。

‘图6.15 史密斯补偿后的控制系统由控制器D(s)和史密斯预估器组成的补偿回路称为纯滞后补偿器，其传递函数为'()()1()()(1)s p D s D s D s G s e τ-=+- (6.44) 根据图6.15可得史密斯预估器补偿后系统的闭环传递函数为 '()()()1()()p s p D s G s s e D s G s τ-Φ=+ (6.45)由式(6.45)可以看出，经过补偿后，纯滞后环节在闭环回路外，这样就消除了纯滞后环节对系统稳定性的影响。

拉氏变换的位移定理说明e -τs仅仅将控制作用在时间座标上推移了一个时间τ，而控制系统的过渡过程及其它性能指标都与对象特性为G p (s)时完全相同。