用S7_200PLC实现Smith预估控制

s7 200 plc课程设计一、课程目标知识目标：1. 理解S7-200 PLC的基本结构、工作原理及功能特点；2. 掌握PLC编程软件STEP 7-Micro/WIN的使用方法；3. 学会使用PLC指令进行逻辑控制程序的设计与调试；4. 了解PLC在工业自动化中的应用场景。

技能目标：1. 能够独立完成S7-200 PLC的硬件接线；2. 能够运用PLC编程软件进行程序编写、下载和调试；3. 能够运用PLC指令进行简单逻辑控制程序的设计与实现；4. 能够分析并解决PLC控制系统中的常见问题。

情感态度价值观目标：1. 培养学生对工业自动化技术的兴趣，激发学习热情；2. 培养学生团队合作意识，学会与他人共同解决问题；3. 培养学生严谨、细致、负责的学习态度，注重实践操作的安全性；4. 增强学生对我国工业发展的认识，提高国家自豪感。

课程性质：本课程为实践性较强的专业课程，旨在培养学生掌握S7-200 PLC 的基本知识和操作技能。

学生特点：学生具备一定的电工电子基础知识，对PLC有一定了解，但实际操作经验不足。

教学要求：注重理论与实践相结合，强调实际操作能力的培养，提高学生解决实际问题的能力。

通过本课程的学习，使学生能够达到以上设定的知识、技能和情感态度价值观目标。

在教学过程中，将目标分解为具体的学习成果，以便进行后续的教学设计和评估。

二、教学内容1. S7-200 PLC硬件结构及功能特点：介绍PLC的基本组成、输入输出模块、通信模块等，使学生了解PLC硬件系统的搭建。

相关教材章节：第一章PLC概述。

2. PLC编程软件STEP 7-Micro/WIN操作：学习编程软件的安装、使用及基本操作，为后续编程打下基础。

相关教材章节：第二章PLC编程软件操作。

3. PLC指令系统：学习基本逻辑指令、定时器/计数器指令、比较指令等，为逻辑控制程序设计提供支持。

相关教材章节：第三章PLC指令系统。

4. PLC程序设计与调试：学习逻辑控制程序的设计方法、调试技巧，使学生具备实际操作能力。

实验报告实验名称：Smith预估控算法设计仿真实验课程名称：计算机控制与组成学生姓名；专业班级:自动化1001 学生学号：实验时间：2013.5.7****：**：一、实验目的在控制算法学习的基础上，根据给定对象特性设计Smith 预估控制器算法，并利用Matlab 软件进行仿真实验，同时与PID 控制算法进行比较，加深对该控制算法的掌 握和理解。

二、实验内容和要求实验内容：设广义被控对象为：1011()()()1Ts sse e H s G s G s es T sττ----==⋅+控制系统框图为：T取T=1、τ=2、T 1=2.88，经采样（T=1s ）保持后，其广义对象z 传递函数为00.2934()0.7066G z z =-， 而2se -转换为2个单位迟延。

控制器参数：Kp=0.5，Ki=0.2，Kd=0。

实验要求：(1)设计smith 预估控制算法，作给定值扰动和外部扰动响应实验，并绘制控制器输出P 和系统输出y 响应曲线。

（2）被控对象不变，采用理想PID 进行给定值扰动和外部扰动响应实验，并绘制控制器输出P 和系统输出y 响应曲线。

三、实验步骤1.根据实验原理图在Matlab 中搭建如下仿真结构图：上图中，上面的回路为Smith预估控制器与对象所构成的回路，下面的回路为PID控制算法与被控对象所构成的回路，通过scope可以看到两种控制算法对扰动产生的响应曲线，分别在两条回路中加入给定值扰动和二次扰动，且注意两次扰动加入的时间间隔开，以便观察两种算法对不同扰动的克服情况。

2.在搭建好的模型中给控制器设定参数，加入阶跃扰动，两次扰动时间差为30s，对系统进行仿真，记录仿真曲线。

3.保持Smith与控制算法回路参数不变，改变PID控制算法参数，使其响应曲线接近用Smith控制算法控制所得到的曲线，记录最接近时的两条曲线并记录此时PID 参数。

四、实验结果及分析1.控制器参数：Kp=0.5，Ki=0.2，Kd=0时，两种控制算法得到的曲线：（其中蓝色的为Smith算法控制下得到的阶跃响应曲线，绿线则为常规PID控制下得到的曲线）2.保持Smith预估控制器参数不变，调整PID调节器参数使其接近响应曲线接近前者的图此时对应的PID控制器的参数为：Kp=0.45，Ki=0.15，Kd=0。

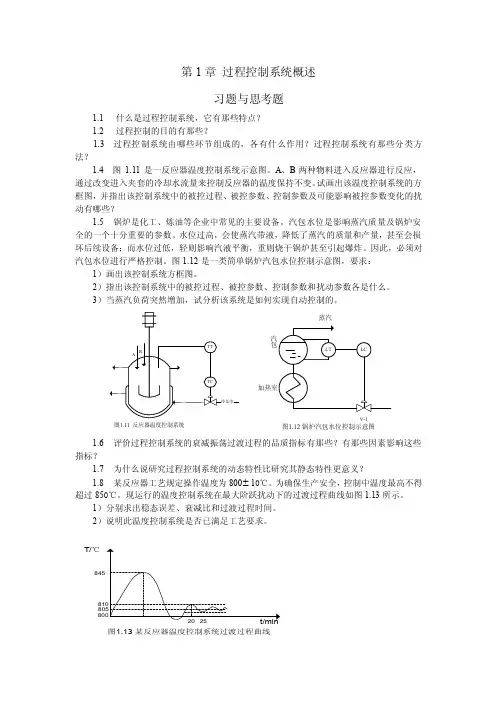
第1章 过程控制系统概述习题与思考题1.1 什么是过程控制系统，它有那些特点？1.2 过程控制的目的有那些？1.3 过程控制系统由哪些环节组成的，各有什么作用？过程控制系统有那些分类方法？1.4 图1.11是一反应器温度控制系统示意图。

A 、B 两种物料进入反应器进行反应，通过改变进入夹套的冷却水流量来控制反应器的温度保持不变。

试画出该温度控制系统的方框图，并指出该控制系统中的被控过程、被控参数、控制参数及可能影响被控参数变化的扰动有哪些？1.5 锅炉是化工、炼油等企业中常见的主要设备。

汽包水位是影响蒸汽质量及锅炉安全的一个十分重要的参数。

水位过高，会使蒸汽带液，降低了蒸汽的质量和产量，甚至会损坏后续设备；而水位过低，轻则影响汽液平衡，重则烧干锅炉甚至引起爆炸。

因此，必须对汽包水位进行严格控制。

图1.12是一类简单锅炉汽包水位控制示意图，要求：1）画出该控制系统方框图。

2）指出该控制系统中的被控过程、被控参数、控制参数和扰动参数各是什么。

3）当蒸汽负荷突然增加，试分析该系统是如何实现自动控制的。

V-1图1.12 锅炉汽包水位控制示意图1.6 评价过程控制系统的衰减振荡过渡过程的品质指标有那些？有那些因素影响这些指标？1.7 为什么说研究过程控制系统的动态特性比研究其静态特性更意义？1.8 某反应器工艺规定操作温度为800 10℃。

为确保生产安全，控制中温度最高不得超过850℃。

现运行的温度控制系统在最大阶跃扰动下的过渡过程曲线如图1.13所示。

1）分别求出稳态误差、衰减比和过渡过程时间。

2）说明此温度控制系统是否已满足工艺要求。

T/℃图1.13 某反应器温度控制系统过渡过程曲线1.9 简述过程控制技术的发展。

1.10 过程控制系统与运动控制系统有何区别？过程控制的任务是什么？设计过程 控制系统时应注意哪些问题？第3章 过程执行器习题与思考题3.1 试简述气动和电动执行机构的特点。

3.2 调节阀的结构形式有哪些？3.3 阀门定位器有何作用？3.4 调节阀的理想流量特性有哪些？实际工作时特性有何变化？3.5 已知阀的最大流量min v q =50m 3，可调范围R=30。

第五节 Smith 预估控制Smith 预估控制方法是在1957年由Smith 提出来的，其特点是预先估计被控系统在基本扰动下的动态特性，然后用预估器进行补偿，力图使被延迟的被控制量超前反映到控制器中，使控制器提前动作，从而显著地减小系统的超调量，同时加速系统的调节过程。

一、Smith 预估控制原理预估控制系统原理图如图7-24所示。

(a) 预估控制系统原理框图 (b) Smith 预估器图7-24 预估控制系统原理图 图中，s e s G τ−)(p 为具有时滞为τ的对象传递函数，其中)(p s G 为被控对象；)(m s G 为内部模型（又称为对象的标称或名义模型），即Smith 预估器的传递函数，()s e s G s G τ−−=1)()(p m ；)(s D 为（前馈）内模控制器；)(s d 为扰动；)(s R 为参考输入；)(s Y 为被控对象输出；)(m s Y 为内部模型输出。

由图7-24可知，将Smith 预估器与控制器（或被控对象）二者并联。

在理论上可以使被控对象的时间滞后得到完全补偿，控制器的设计就不必再考虑对象的时滞作用了。

现在，系统中假设没有补偿器（预估器），则控制器输出与被控量之间的传递函数便为 s e s G s U s Y τ−=)()()(p (7-50) 上式表明，受到)(s U 控制作用的被控量)(s Y 要经过纯滞后时间τ之后才能反馈到系统控制器输入端。

若采用预估补偿器，则控制量)(s U 与反馈到控制器输入端的反馈信号)(s Y ′之间的传递函数乃是两个并联通道之和，即)()()()(m p s G e s G s U s Y s +=′−τ (7-51) 为使反馈信号)(s Y ′不发生时间滞后τ，则要求(7-51)式满足)()())(()()(p m p s G s G e s s G s U s Y s =+=′−τ (7-52) 于是，就导出了Smith 预估补偿器的传递函数为()s e s G s G τ−−=1)()(p m (7-53) 在系统中设置了Smith 预估器的情况下，可以推导出系统的闭环传递函数为)()(1)()()1)(()(1)()(1)1)(()(1)()()()(p p p p p p s G s D e s G s D e s G s D e s G s D e s G s D e s G s D s R s Y s s s s+=−++−+=−−−−−ττττ (7-54) 由上式可以明显看出，在系统的特征方程中，已经不含有s e τ−项。

东南大学能源与环境学院实验报告课程名称：实验名称：院（系）：专业：姓名：杨康学号：实验室：实验组别：同组人员：实验时间：年月日评定成绩：审阅教师：目录一．实验目的 (3)二．实验内容 (3)三．实验步骤 (3)四．实验分析 (12)实验二 Smith预估控制实验指导书一实验目的通过实验掌握Smith预估控制的方法及程序编制及调试。

二实验内容１．Smith预估控制系统如图所示，图一对象G(S)= K·e-τs / (1+TS),K = 1, T1 = 10 s , τ = 5 s ,1Wc(z)采用数字PI控制规律。

２．对象扰动实验画出U(t) = u0·1(t)时，y(t)曲线。

３．Smith预估控制(1)构造Wτ(S)，求出Wτ(Z)。

(2)整定Wc(s)(按什么整定？)(3)按图仿真，并打印曲线。

（4）改变Wτ(S)中K，τ（对象不变），进行仿真比较，观察它们对调节过程的影响。

三实验步骤1、对象扰动实验（1）差分方程如附录。

（2）源程序如下：#include"iostream.h"#include"math.h"#include"fstream.h"void main(){fstream outfile("data1.xls",ios::out);double t;double u0;cout<<"请输入采样周期:";cin>>t;cout<<"请输入阶跃幅值:";cin>>u0;double ee=pow(2.718,(-t/10.0));int N;int i;double u[100],y[100];for(i=0;i<100;i++){u[i]=u0;y[i]=0.0;}N=1+5/t;for(i=N;i<100;i++){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}for(i=0;i*t<100;i++){cout<<y[i]<<'\t';}for(i=0;i*t<100;i++){outfile<<i*t<<'\t';}outfile<<'\n';for(i=0;i*t<100;i++){outfile<<y[i]<<'\t';}outfile.close();}（3）输出结果：当采样周期T=1，阶跃幅值为1时：Y（t）输出数据：0 0 0 0 0 0 0.0951532 0.181252 0.259159 0.3296520.393438 0.451154 0.503379 0.550634 0.593392 0.6320820.667091 0.698768 0.727431 0.753367 0.776835 0.798070.817284 0.83467 0.850402 0.864637 0.877517 0.8891720.899717 0.909259 0.917894 0.925706 0.932776 0.9391720.94496 0.950197 0.954936 0.959224 0.963104 0.9666150.969792 0.972666 0.975267 0.97762 0.97975 0.9816770.98342 0.984998 0.986425 0.987717 0.988886 0.9899430.9909 0.991766 0.99255 0.993259 0.9939 0.99448 0.9950060.995481 0.995911 0.9963 0.996652 0.996971 0.9972590.99752 0.997756 0.997969 0.998162 0.998337 0.9984960.998639 0.998768 0.998885 0.998991 0.999087 0.9991740.999253 0.999324 0.999388 0.999446 0.999499 0.9995470.99959 0.999629 0.999664 0.999696 0.999725 0.9997510.999775 0.999796 0.999816 0.999833 0.999849 0.9998630.999876 0.999888 0.999899 0.999908 0.999917阶跃响应曲线如下：图二2、Smith预估控制（1）差分方程见附录：（2）源程序如下：#include"iostream.h"#include"math.h"#include"fstream.h"void main(){fstream outfile("data1.xls",ios::out);double t,kp,ki;int t1,k;cout<<"请输入Wt(s)中的K:";cin>>k;cout<<"请输入Wt(s)中的迟延时间t:";cin>>t1;cout<<"请输入采样周期:";cin>>t;cout<<"请输入PI调节器的参数kp:";cin>>kp;cout<<"请输入PI调节器的参数ki:";cin>>ki;double ee=pow(2.718,(-t/10.0));int N,N1;int i;double r[100],e1[100],e2[100],cm[100],q[100],u[100],y[100];for(i=0;i<100;i++){r[i]=1.0;e1[i]=0.0;e2[i]=0.0;u[i]=0.0;y[i]=0.0;cm[i]=0.0;q[i]=0.0;}N=1+5/t;N1=t1/t;cout<<N<<'\t'<<N1<<endl;for(i=0;i<100;i++){if(i==0){e1[i]=r[i];cm[i]=0;q[i]=0;e2[i]=e1[i]-q[i];u[i]=kp*e2[i]+ki*e2[i];}if(i>0&&i<N1){e1[i]=r[i]-y[i-1];cm[i]=ee*cm[i-1]+k*(1-ee)*u[i-1];q[i]=cm[i];e2[i]=e1[i]-q[i];u[i]=u[i-1]+kp*(e2[i]-e2[i-1])+ki*e2[i];if(i>=N){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}}if(i>=N1){e1[i]=r[i]-y[i-1];cm[i]=ee*cm[i-1]+k*(1-ee)*u[i-1];q[i]=cm[i]-cm[i-N1];e2[i]=e1[i]-q[i];u[i]=u[i-1]+kp*(e2[i]-e2[i-1])+ki*e2[i];if(i>=N){y[i]=(1-ee)*u[i-N]+y[i-1]*ee;}}}for(i=0;i*t<100;i++){cout<<y[i]<<'\t';}for(i=0;i*t<100;i++){outfile<<i*t<<'\t';}outfile<<'\n';for(i=0;i*t<100;i++){outfile<<y[i]<<'\t';}outfile.close();}（3）输出结果：以下所涉及到的采样周期均为T=1，PI控制器的参数均为Kp=1，Ki=1；当Smith预估器中的K=1，延迟时间τ=5时（即与对象的特性完全符合）：Y（t）输出数据：0 0 0 0 0 0 0.190306 0.421441 0.663641 0.8917551.08676 1.23639 1.37128 1.47104 1.5311 1.549551.52761 1.46956 1.38931 1.29344 1.18983 1.085670.987246 0.89981 0.828799 0.776983 0.745653 0.7345240.741955 0.765251 0.801257 0.846217 0.896223 0.947450.996402 1.04011 1.07631 1.1035 1.1209 1.12848 1.126831.11708 1.10079 1.07973 1.05581 1.03093 1.00680.984919 0.966463 0.952253 0.942744 0.938032 0.937890.941816 0.949101 0.958895 0.970279 0.982333 0.9941951.00511 1.01448 1.02186 1.02698 1.02978 1.030321.02882 1.02561 1.02108 1.01569 1.00987 1.004060.998627 0.993893 0.990086 0.98735 0.985745 0.9852490.985771 0.987163 0.989238 0.991783 0.994581 0.997421.00011 1.0025 1.00445 1.0059 1.0068 1.00715 1.0071.00641 1.00547 1.00428 1.00293 1.00155 1.000220.999027 0.998028 0.997269 0.996773扰动曲线如下：图三当Smith预估器中的K=1，延迟时间τ=2时（即与对象的特性不完全符合）：Y（t）输出数据如下：0 0 0 0 0 0 0.190306 0.421441 0.663641 0.9279711.21095 1.50619 1.810532.08577 2.31463 2.489892.60123 2.63889 2.59562 2.46564 2.25095 1.958931.59989 1.18774 0.740093 0.277571 -0.176632 -0.598368-0.963966 -1.25121 -1.44044 -1.51579 -1.4662 -1.28642-0.977633 -0.547714 -0.0112532 0.610765 1.29164 1.999962.700933.358 3.934554.39588 4.71103 4.854644.80862 4.56351 4.11952 3.48712 2.68715 1.750360.716479 -0.367272 -1.44817 -2.47036 -3.37751 -4.11571-4.63639 -4.89916 -4.87439 -4.54543 -3.91026 -2.98249-1.79168 -0.38278 1.18524 2.8415 4.5062 6.09408 7.518558.69603 9.55045 10.0176 10.0494 9.61689 8.713477.35632 5.58704 3.47109 1.09587 -1.43244 -3.99312-6.45626 -8.68888 -10.5616 -11.9554 -12.7687 -12.9234-12.3704 -11.0941 -9.11507 -6.49149 -3.31832 0.2752394.13026 8.06445 11.88 15.3731 18.3435扰动曲线如下：图四当Smith预估器中的K=2，延迟时间τ=2时（即与对象的特性不完全符合）：Y（t）输出数据如下：0 0 0 0 0 0 0.190306 0.385225 0.546344 0.7250840.920371 1.11455 1.30834 1.46909 1.59338 1.692661.7608 1.79027 1.78227 1.73766 1.66147 1.560211.43778 1.29949 1.15302 1.00558 0.863901 0.7341210.621319 0.529913 0.463425 0.423874 0.411896 0.4269230.467201 0.529943 0.611457 0.707298 0.812552 0.9221031.03084 1.13389 1.22683 1.30585 1.36793 1.410941.4337 1.43598 1.41848 1.38278 1.33121 1.266721.19274 1.11298 1.03127 0.951381 0.876845 0.8108160.75594 0.714253 0.687116 0.675179 0.67838 0.6959770.726605 0.768367 0.818936 0.875681 0.935797 0.9964341.05484 1.10845 1.15505 1.19281 1.22037 1.236891.24206 1.23609 1.21971 1.19405 1.16064 1.12131.07804 1.03296 0.988182 0.945705 0.907359 0.8747110.849012 0.831146 0.82161 0.820506 0.82755 0.8421020.863208 0.889656 0.920041 0.952835 0.986462 1.01937扰动曲线如下：图五四实验分析当系统是特征方程中含有纯迟延项的时候，系统的闭环稳定性事下降的，当迟延时间τ比较大的时候，系统就会不稳定。

S7-200计件实验实验目的本实验旨在通过S7-200 PLC（可编程逻辑控制器）对计件实验进行控制和监测，以了解PLC的基本概念和运作原理，并提升学生在工业自动化领域的实际操作能力。

实验仪器和材料•Siemens S7-200 PLC•计件机•传感器•操作面板•电缆•电源实验原理S7-200是西门子公司推出的一种低端PLC，具有简单、灵活、易用的特点。

它通常用于小规模的自动化控制系统，如计件实验等。

在计件实验中，我们使用计件机来计数并记录产品的数量。

通过传感器和PLC的连接，我们可以将传感器的信号输入到PLC中，PLC再根据设定的逻辑程序控制计件机进行计数和显示。

实验步骤1.首先，将PLC的电源和计件机的电源接入，并确保电源连接正确。

2.连接传感器和PLC，将传感器的输出信号接入PLC的输入端口（通常为I/O口）。

3.使用适配的编程软件进行PLC的编程，根据实验要求设置适当的计数逻辑和显示方式。

4.将编写好的PLC程序下载到PLC中，确保程序成功加载。

5.正式开始计件实验，观察计件机的计数情况和PLC 的显示效果。

6.根据实验要求调整计数逻辑和显示方式，再次进行实验。

7.实验结束后，关闭计件机和PLC的电源，拔出相关连接。

实验注意事项1.在操作PLC时，遵循正确的操作顺序和安全规范，以免造成电路短路或其他意外情况。

2.调试PLC程序时，谨慎设置逻辑条件和输出信号，以避免错误操作。

3.串联连接过程中，确保接线正确，避免反向插入或松动连接。

4.实验结束后，及时断开电源，并保存实验数据和编程文件。

实验结果分析通过这次实验，我们可以掌握PLC的基本操作和编程技巧，了解计件实验的原理和方法。

通过计数机和PLC的互联互通，我们可以实现实时监测和控制产品数量，提高生产效率和品质。

实验总结本实验通过S7-200 PLC对计件实验进行控制和监测，掌握了PLC的基本概念和运作原理。

通过实际操作，我们对PLC的编程和调试有了更深的理解，同时也了解了计件实验的应用场景和意义。

S7-200smart PLC模拟量输入模块使用说明当我们在实际的应用中需要对当前的温度或是压力进行采集显示的时候，我们需要用到模拟量模块来对模拟量信号进行采集，在这里我们以S7-200smart PLC的EMAE04模拟输入模块为例来说明如何使用这个模块来采集温度或是压力。

例如：现需要实时监控发电机机组的温度，假设变送器输出的信号为0到10V的电压信号，最大温度值为150。

最小温度值为0度。

要完成正确读取实际的温度值，需要进行以下三步操作：第一、正确的接线第二、正确的硬件组态第三、编写正确的程序1、按照变送器提供的信号输出接线方式进行正确的接线，对于EMAE04模块的信号接入如图所示：若变送器为三线制输出的变送器，则接线时，先把变送器的24V电源接上，变送器上的信号输出接端0+，0-端子接24V电源负。

2、打开S7-200smart的编程软件，打开其系统块对其进行硬件组态。

如图所示：注意：对于信号类型的选择，通道0的设置对通道1的设置也有效，通道2的设置对通道3 也同样有效。

3、编写转换程序S7-200smartPLC来说其最大的数字量为27648。

我们可以根据其得到的数字量的大小转换成我们实际的温度值。

对其转换程序，我们可以使用S7-200中的scaling模拟量转换库，使用库移植的方法把其移植到S7-200smart的软件中。

其移植方法可以参考前面所介绍的内容。

Input :表示需要转换的数字量，即采样所的数字量Ish：换算对象的高限，即最大模拟量所对应的数字量值（27648）Isl: 换算对象的低限，即最小模拟量所对应的数字量值（0）Osh：换算结果的高限，即测量范围最大值Osl：换算结果的底限，即测量范围最小值。

VD100：换算结果所存储的值。

第二部分：如何引用模拟量的地址在软件中，就可以看到，以上模块量模块的地址就是：AIW16 18 20 22AIW32 34 36 38。

基于S7PLC的史密斯预估补偿控制的实现
杨家骥
【期刊名称】《自动化与仪器仪表》
【年(卷),期】2010()3
【摘要】介绍了一种改进型史密斯预估补偿控制方案的实现,比较详细叙述了史密斯预估器S7程序,并对控制系统进行了仿真。

【总页数】4页(P66-69)
【关键词】可编程控制器;控制;史密斯预估器;仿真
【作者】杨家骥
【作者单位】上海博凯石化设备检修安装有限公司
【正文语种】中文
【中图分类】P273
【相关文献】
1.磁流变半主动悬架的史密斯预估-LQG时滞补偿控制方法 [J], 王健;祖广浩
2.磁流变半主动悬架的史密斯预估-LQG时滞补偿控制方法 [J], 王健;祖广浩
3.史密斯预估补偿控制及MATLAB仿真 [J], 杨海勇
4.基于史密斯预估补偿及自整定PID的过热汽温控制方案 [J], 焦健
5.史密斯预估补偿控制与PID控制的比较研究 [J], 陆萍蓝;张火明;毛汝东
因版权原因，仅展示原文概要，查看原文内容请购买。

第29卷第4期江苏理工学院学报JOURNAL OF JIANGSU UNIVERSITY OF TECHNOLOGY Vo l.29，No.4 Aug.，20232023年8月随着大数据与物联网技术的快速发展以及节能环保理念的深入人心，城市建设也开始向智能化、绿色化方向发展[1-2]。

城市供水系统管网铺设复杂，分布范围广，具有非线性、时滞性和用电量大等特点[3]。

在节能方面，采用PLC控制变频器调速的供水方式，具有节能、控制方便等优点[4]，可以有效降低城市供水系统的用电量。

在水压控制技术方面，由传统PID控制的恒压供水变频调速系统，尽管控制精度较高[5]，但是，存在参数整定复杂、调节时间长、抗干扰性差等问题[6]。

模糊控制可以防止传统PID控制器适应能力差等弊端，但是，往往在系统稳定运行期会出现供水压力偏差[7-8]。

模糊免疫PID控制结合了免疫控制的自适应性和传统PID控制的优点，在系统稳定运行时产生的偏差较小[9]；然而，上述控制技术主要是在常规PID控制规则中采用模糊控制或其他方法整定控制参数，更侧重于对常规PID技术的改进，而未充分考虑恒压供水系统中存在的时滞问题。

利用Smith预估器可以减弱系统中时滞环节引起的超调或者振荡[10]。

因此，针对城市供水系统的时滞和抗干扰问题，可以把改进的PID控制算法与Smith预估有机地结合起来。

本文针对恒压供水系统，提出了一种基于Smith预估器的模糊免疫PID控制策略，该方法综合了Smith预估、模糊免疫控制以及PID控制三者的优点。

1变频恒压供水系统如图1所示，城市变频供水系统由压力传感器、PLC控制器、变频器、交流电机、蓄水池、供水管网和水泵组成[11]。

其中：压力传感器为反馈检测机构；变频器为驱动机构；交流电机为执行机构；水泵为控制对象；PLC控制器为控制机构。

压力基于Smith预估的恒压供水系统模糊免疫PID控制研究李广军，武瑞杰，李文强（江苏理工学院汽车与交通工程学院，江苏常州213001）摘要：针对供水系统水压控制存在的时滞、干扰多等特性，设计了一种基于Smith预估的模糊免疫PID控制系统。

S7-200plc原理及应用
S7-200 PLC是西门子公司研发的一种基于微型控制器的集成控制系统。

其原理是通过将各种输入信号进行逻辑运算，再通过输出信号控制各种执行器，从而实现对设备和工艺过程的控制和监测。

S7-200 PLC具有模块化结构，通常由主控模块、输入模块、输出模块和特殊功能模块等组成。

主控模块负责执行用户编写的程序，输入模块用于接收外部的输入信号，输出模块用于控制各种执行器，特殊功能模块则可以扩展系统的功能。

S7-200 PLC广泛应用于各种工业自动化控制领域。

例如，它可以用于自动化生产线上的工艺控制和监测，通过接收传感器信号并控制执行器，实现对生产过程的自动化控制。

它还可以用于建筑物的智能控制系统，如楼宇自动化系统，通过控制照明、空调、安防等设备，提高建筑物的能效和安全性。

S7-200 PLC还可以用于机械设备的控制，如机床控制系统。

通过编写控制程序，可以实现对机床的自动化控制，提高加工精度和生产效率。

同时，它还可以用于电力系统的实时监测和控制，如电力配电系统和电网控制系统，确保电力系统的稳定运行。

综上所述，S7-200 PLC是一种功能强大、可靠性高的控制系统，广泛应用于多个工业领域。

它通过对输入信号进行逻辑运算，再通过输出信号控制执行器，实现对设备和工艺过程的控制和监测，提高自动化水平和生产效率。

S7-200SMARTPLC喷泉系统设计与MCGS控制喷泉，指由地下喷射出地面的泉水；特指人工喷水设备，想必喷泉大家并不陌生，在我们的日常生活中比比皆是，例如：公园花草树木的喷泉，各大商业中心广场喷泉中心等！喷泉系统可以由PLC来控制吗？当然可以，下面就给大家介绍。

01、控制要求使用I0.0来控制M0.0标志位，通过M0.0来启动喷泉系统，喷泉一到喷泉八每隔50秒相互切换并循环与在MCGS触摸屏上显示控制。

02、IO分布表03、设计程序第一步：（启停控制）第二步：（启动定时器）第三步：（控制喷泉一到喷泉八每隔50秒切换并循环。

）04、MCGS组态配置第一步：（选择实际触摸屏对应的型号，这里我是TPC1570Gi这款型号，大家可以根据自己实际触摸屏型号来选择。

）第二步：（工作台—设备窗口—打开设备窗口）第三步：（设备窗口—鼠标右击设备工具箱）第四步：（添加设备）第五步：（添加成功）第六步：（添加设备通道PLC变量）05、MCGS画面设计第一步：（工作台—用户窗口—新建一个窗口—窗口0）第二步：（标签动画—扩展属性—设计标题）第三步：（标签动画—属性设置—静态属性—取消填充与边线）第四步：（标准按钮—属性设置—输入文本）第五步：（标准按钮—操作设置—设置数据对象操作）第六步：（动画显示—基本属性—指示灯）第七步：（动画显示—显示属性—显示变量）喷泉二到喷泉八参照喷泉一以此类推操作第八步：（标签动画—属性设置—勾选显示输出）第九步：（标签动画—扩展属性—输入文字）第十步：（标签动画—显示输出—关联地址）第十一步：（画面设计完成）06、演示效果第一步：（按下启动按钮启动喷泉系统）来源：PLC发烧友，作者：技成-徐陈爽，转载请注明出处！评论处大家可以补充文章解释不对或欠缺的部分，这样下一个看到的人会学到更多，你知道的正是大家需要的。