材料力学 轴向拉压变形.
- 格式:ppt
- 大小:1.32 MB
- 文档页数:44



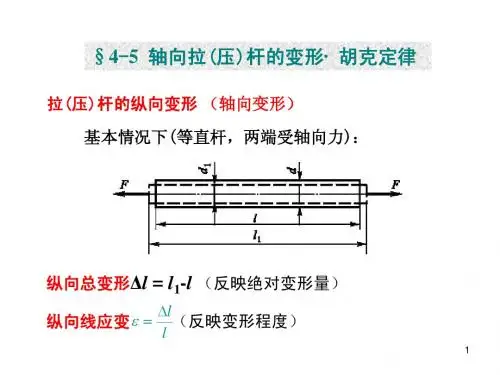




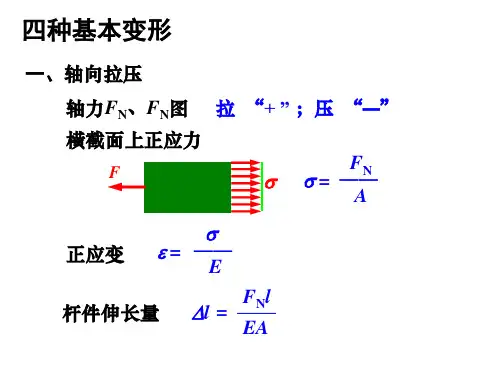

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

02轴向拉压变形材料力学刘鸿文轴向拉压变形是材料力学中一个非常重要的研究领域,涉及到材料在拉伸和压缩加载下的行为和性能。
在这个过程中,材料会发生形变,这种形变会影响到材料的机械性能和工程应用。
本文将对轴向拉压变形及其在材料力学中的应用进行介绍,并结合实际工程案例进行分析。
轴向拉压变形是指材料在受到拉伸和压缩加载时所发生的直线形变。
在轴向拉伸加载下,材料会沿着加载方向延展,而在轴向压缩加载下,材料则会沿着加载方向收缩。
这种形变会引起材料内部晶体结构的改变,从而影响到材料的力学性能。
因此,研究轴向拉压变形对于理解材料行为和优化材料性能具有重要意义。
在研究轴向拉压变形中,最常用的方法是通过应力-应变曲线来描述材料的拉伸和压缩性能。
应力-应变曲线可以反映材料在加载过程中的应力和应变之间的关系,从而揭示材料的变形行为。
在拉伸加载下,应力-应变曲线通常包含线性弹性阶段、屈服阶段和断裂阶段;而在压缩加载下,应力-应变曲线通常包含线性弹性阶段、屈服阶段和塑性变形阶段。
通过分析应力-应变曲线,可以了解材料的强度、韧性、延展性等性能,为工程设计和材料选型提供依据。
除了应力-应变曲线外,轴向拉压变形还可以通过应力、应变、变形、变形速率等参数来进行研究。
通过测量材料的应力、应变和变形等物理量,可以进一步了解材料的变形机制和行为。
在实际工程中,还可以通过数值模拟和实验测试来验证轴向拉压变形的理论。
在工程中,轴向拉压变形的研究对于设计和优化结构和材料具有重要意义。
例如,在航空航天领域,材料需要承受复杂的载荷和环境,对材料的轴向拉压变形性能要求较高。
通过研究材料的轴向拉压变形行为,可以选择合适的材料和加工工艺,从而提高结构的安全性和可靠性。
总之,轴向拉压变形是材料力学中一个重要的研究方向,对于理解材料的行为和性能具有重要意义。
通过研究材料的轴向拉压变形,可以为工程设计和材料选择提供重要的参考和指导,推动材料科学和工程技术的发展。