轴向拉压变形
- 格式:doc
- 大小:2.38 MB
- 文档页数:10



简述轴向拉压杆的受力特点和变形特点
轴向拉压杆是一种受到拉力或压力作用的杆件。
其受力特点主要
有两点:
1. 受力方向:轴向拉压杆受力方向与其轴线方向相同或相反。
当受到拉力时,轴向拉压杆会向外展开;当受到压力时,轴向拉压杆
会向内收缩。
受力方向与轴线方向共线,使得杆件能够承受较大的拉
力或压力。
2. 受力均匀:轴向拉压杆受力均匀分布在其截面上。
由于受力
方向与轴线方向相同或相反,杆件内部的各个截面上的应力相对均匀。
这样的受力特点能够保证杆件的强度和刚度。
轴向拉压杆的变形特点主要有两点:
1. 长度变化:轴向拉压杆在受到拉力或压力作用时会发生长度
的变化。
当受到拉力时,轴向拉压杆会发生伸长变形;当受到压力时,轴向拉压杆会发生缩短变形。
杆件的长度变化与受力的大小成正比。
2. 弯曲变形:轴向拉压杆在受力作用下有可能发生弯曲变形。
当受到较大的压力或拉力时,杆件可能会产生塑性弯曲或弹性弯曲。
这种变形可能会影响杆件的稳定性和工作性能。
综上所述,轴向拉压杆的受力特点是受力方向与轴线方向相同或
相反,受力均匀;变形特点是发生长度变化和有可能出现弯曲变形。
这些特点需要在杆件的设计和使用过程中进行考虑,以保证其性能和
安全。


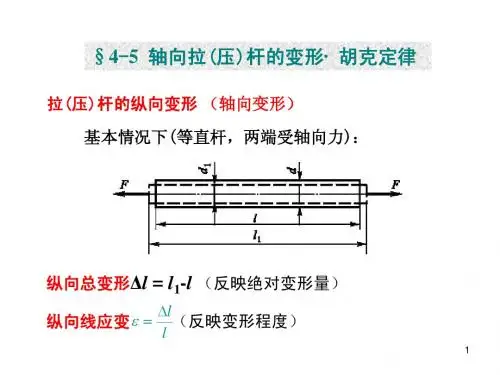
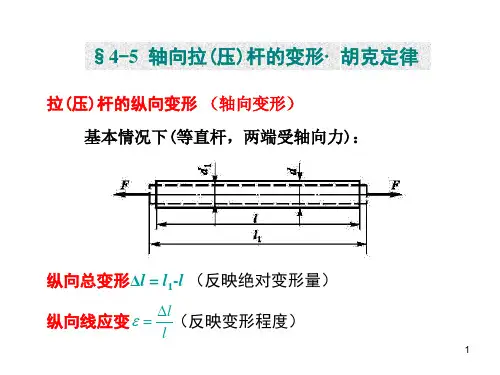
轴向拉伸或压缩的受力(变形)特点
在固体力学中,轴向拉伸或压缩(直轴)是指在杆件上加施一些受力,使其长度单向变化的加载方式,其受力(变形)行为典型的表现出特定的受力特征。
在直轴受力(变形)中,特定的受力特征包括非线性的轴向拉伸或压缩力学性能。
一般来说,轴向拉伸或压缩条件下加载固体时,固体的变形会随着载荷的增加而逐渐加大。
这一变形通常以增加的形式表示,而且可能伴随着扭转变形。
轴向拉伸或压缩条件下受力(变形)的另一个典型特征是大载荷时的弹性恢复性能,这是由于在轴向拉伸或压缩作用下,固体会经历一段加强期,而在达到非线性变形以及回弹时,力学性能又会有一段衰减期。
在实际应用中,受力(变形)过程需要充分考虑弹性恢复性能,以保证固体力学性能。
直轴受力(变形)的表现为应力-应变曲线,而应变的月的和特点也反映出固体的塑性行为。
此外,固体在应变过程中可能出现低周疲劳行为,此类现象反应出它的受力(变形)突变。
轴向拉伸或压缩受力(变形)的特点可以从分析中提取出来,这些特点包括受力随载荷的变化规律,受力弹性恢复以及对疲劳等应力及应变测试中的特殊行为。
直轴受力(变形)特点可以从几何变形、受力数据、图像处理和材料记录等方面来断定,以确定该结构的应变特征。
总之,轴向拉伸或压缩受力(变形)的特点是其受力行为表现出特定的力学特征,这些特征可以通过分析、观察等手段来确定,而这些特征对于掌握该结构及其力学性能有重要意义。




第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(c)解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(d)解:(1)求指定截面上的轴力(2)作轴力图中间段的轴力方程为:轴力图如图所示。
[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
解:(1)求指定截面上的轴力(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成,其截面均为两个的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EC横截面上的应力。
解:(1)求支座反力由结构的对称性可知:(2)求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断,取左部分为研究对象,其受力图如图所示。
由平衡条件可知:②以C节点为研究对象,其受力图如图所示。
由平平衡条件可得:(3)求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为:[习题2-5] 石砌桥墩的墩身高,其横截面面尺寸如图所示。
荷载,材料的密度,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:墩身底面积:因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
[习题2-6]图示拉杆承受轴向拉力,杆的横截面面积。
如以表示斜截面与横截面的夹角,试求当时各斜截面上的正应力和切应力,并用图表示其方向。
解:斜截面上的正应力与切应力的公式为:式中,,把的数值代入以上二式得:轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。
轴向拉压构件的受力特点与变形特点
一、轴向拉压构件受力特点
1、受力情况
轴向拉压构件的受力情况分为两种:拉紧状态和拉伸状态。
拉紧状态下受力规律是:轴向拉力的大小和导管长度有关,当导管长度增加时,拉力随之增大,反之亦然;拉伸状态下,受力规律是:拉力的大小和导管外径有关,当导管外径增加时,拉力随之增大,反之亦然。
2、结构及受力特点
轴向拉压构件的结构特点是具有空心结构,受力特点是在拉紧状态下受力均布,当拉伸时,受力不均布,中间部分受力较小,两端受力较大。
二、轴向拉压构件变形特点
1、变形特点
轴向拉压构件的变形特点是:拉紧状态下,由于受力均布,所以变形也均布,可以满足设计要求;拉伸状态下,由于受力不均布,会出现拉伸构件中间部分变形较小,两端变形较大的现象。
2、塑性变形
轴向拉压构件的受力大小和变形特点决定了其塑性变形的大小,当受力大时,塑性变形会大于变形要求值,当受力小时,塑性变形会小于变形要求值。
另外,还有一点要注意,塑性变形是随着受力增加而增加,当受力越大,塑性变形程度也会越大。
- 1 -。
1上海工程技术大学基础教学学院工程力学部1第三章 轴向拉压变形§3—1 轴向拉压杆的变形 §3—2 桁架的节点位移 §3—3 拉压与剪切应变能 §3—4 简单拉压超静定拉压变形小结2一、概念§3—1 轴向拉压杆的变形1、轴向变形:轴向尺寸的伸长或缩短。
2、横向变形:横向尺寸的缩小或扩大。
3三、叠加原理①当各段的轴力为常量时—— L L1 L 2 L 3 F Ni L i EA i几个载荷同时作用所产生的变形,等于各载荷单独作用时产生的变形的总和 — 叠加原理②当轴力为x的函数时 N=N(x)—— L d L1 d L2 d L3 FN ( x)dx L EA(3)、使用条件:轴向拉压杆,弹性范围内工作。
应力与应变的关系:(虎克定律的另一种表达方式)L FN L EAFN E L AL E5小结: 变形——构件在外力作用下或温度影响下所引起的形状尺 寸的变化。
弹性变形——外力撤除后,能消失的变形。
塑性变形——外力撤除后,不能消失的变形。
位移——构件内的点或截面,在变形前后位置的改变量。
线应变——微小线段单位长度的变形。
62A aB aCFxF2F 3F例:已知杆件的 E、A、F、a 。
求:△LAC、δ B(B 截面位移) ε AB (AB 段的线应变)。
解:1、画FN 图: 2、计算:FN (1).L FN L EALACLABLBC Fa EA3Fa EA 4Fa EA(2). B LBC( 3 ). AB 3FaEA L AB L ABFa aEA F EA7§3—2 桁架节点位移三角桁架节点位移的几何求法。
怎样画小变形放大图?分析:1、研究节点 C 的受力,确定各杆的内力 FNi;AL1B 2、求各杆的变形量△Li;L2F1F2C3、变形图严格画法,图中弧线; (1) 以A为圆心,AC1为半径画弧线;CL1 (2) 以B为圆心,BC2为半径画弧线;F L2 FC1交点C’就是C点实际位移。
4、变形图近似画法:C2C ''以切线代替图中弧线。
C'C '' 就是C点近似位移。
8写出图 2 中 B 点位移与两杆变形间的关系L1BAl2l 1 B1L2F分析: 一、受力分析: 二、画B点的变形图:1)画沿原杆伸长或缩短线; 2)作伸长或缩短线端点垂线;C 图2拉 S1 压 S2vB BB2B2 BFB’交点就是节点B的位移点。
3) B点水平位移:uB BB1 L1B'B点垂直位移:vB L1ctg L2 sin B u2 BvB29例:杆1为钢管,A1= 100 mm²,E1 = 200 GPa,L1= 1 m ;杆2为硬铝管,A2= 250 mm²,E2 = 70 GPa,P = 10 kN。
试求:节点A点的垂直位移。
N1解:1)求各杆内力B CN2 l1A PA2 45 Al2l1N1 2P 14.14kN , N 2 P 10kN2)求各杆的伸长lil1N1l1 0.707, E1 A1l2N 2l2 E2 A20.404mm3)画A点的位移图AA5 AA4 A4 A5PA1AA4 l1 / cos 45 A4 A5 l2ctg 4545 A4AA5l1 cos 45l2ctg 450.99990.404 AA5 1.404 mmA3A510例 :设横梁 ABCD 为刚梁,斜杆A=440mm²,E = 70kN,P1= 5kN,P1 A A1P2=10kN,L=1m;试求:AP2 60lClB AY C1D点的垂直位移。
30 (不计横梁变形)解:1)、CD杆内力:研究对象 AB mB 0 : P12l (P2 NC sin 30)l 0 N C 40 ( kN )2) CD杆的变形:P1P2ACYBBXBL NClCD NCl 1.5 (mm) EA EA cos 3)杆A.C点的变形图:CC 2 lACNC B CY CC1 CC 2 cos l sin C2ABA1 AY AA1 CC 1 2 CYCY C1 AY 2 CY 2l 6 (mm) sin 11§3—3 拉压应变能一、应变能概念1、外力功:W固体受外力作用而变形,在变形过程中外力所做的功。
W 1 P l 22、应变能:V 固体在外力作用下,P l因变形而储存的能量。
V1 2N l1 2NNl EAN 2l 2EA3、能量守恒:W V4、应变能密度:单位体积内储存的能量。
v V /Vl PPioli ld (l )123应变能密度:v V /V应变能:VN 2l EA,体积:V A lv V VN 2l 2EA1 AlN2 2 A21 E 2 1 2E 2dxdyv1 22 2E5、剪切应变能密度:dx'dz2 v 2G G:剪切弹性模量 dy 单元体: dV dxdydzdz'13二、求结构节点位移的能量法:例:杆1为钢管,A1= 100 mm²,E1 = 200 GPa,L1= 1 m ;杆2为硬铝管,A2= 250 mm²,E2 = 70 GPa,P = 10 kN。
试求:节点A点的垂直位移。
N1解:1)求各杆内力B 45CN2 l1A PA2 AYA A1N1 2P 14.14kN , N 2 P 10kN2)求外力功及各杆的变形V能iW1 2PAY,V 1N12l1 , 2E1 A1V 2N 22l2 2E2 A23)能量守恒W V1 V 2A3 P P AY2(V1 V1) P 1.404 mm14例:各杆截面A,材料E相同。
试求:节点 A 点的垂直位移。
B解:1)求各杆内力45 312l CA AY N1N2APPXB BN3N1N1 2P, N2 N3 P2)求外力功及各杆的变形V能iW1 2P3)A能Y, V量1 守 2恒NE112lA1W1 ,V 2 V 3 V1 V 2 N22l2 2E2 A2 V 31 2PAYN12l1 2E1 A1 2 N22l2 2E2 A21 2P AY(2P)2 2EA2l (P)2 l 2 2EA AY2Pl( 2 EA 1)15例 :设横梁 ABCD 为刚梁,斜杆A=440mm²,E = 70GP,P1= 5kN,P2=10kN,L=1m;试求:A 点的垂直位移。
30 (不计横梁变形)P1Al AY A1P2 60ClBC1D解:1)、CD杆内力:研究对象 AB mB 0 : P12l (P2 NC sin 30)l 0 N C 40 ( kN )2) 求外力功与杆的变形能:P1P2ACW W1 WV2 , ,YBBXBW11 2P1Ay,W21 2P2 Cy,VN 2lCD 2 EA,AC AY A1 CY C1NC B Ay 2 Cy W3) 能量守恒:W Ay V2( P1P2 2), AY22N2 CDlCD(2P1 P2 ) 2EA6(mm)16§3 - 4 拉压超静定一、概念 1、静定:结构或杆件的未知力个数等于有效静力方程的个数,只利用有效静力方程就可以求出所有的未知力。
2、超静定:结构或杆件的未知力个数大于有效静力方程的个数,只利用静力方程不能求出所有的未知力。
N1 N2AX 0, N1 N3 N2PY 0.APBD13C 23、多余约束:在超静定系统中多余维A持结构几何不变性所需要的杆或支座。
P4、多余约束反力:多余约束对应的反力。
175、超静定的次数(按超静定次数划分):BDC超静定次数 = 多余约束个数132= 未知力个数-有效静力方程个数。
A二、求解超静定(关键——变形几何关系的确定) P步骤:1、根据平衡条件列出平衡方程(确定超静定的次数)。
2、根据变形协调条件列出变形几何方程。
3、根据力与变形的物理条件,列出力的补充方程。
L FN L EA4、联立静力方程与力的补充方程求出所有的未知力。
三、注意的问题拉力——伸长变形相对应;压力——缩短变形相对应。
184例:l1 l2 , E1 A1 E2 A2 , E3 A3 ,求:各杆的内力。
解:、平衡方程:BDC X 0 FN1 sin FN 2 sin 0132 Y 0 FN1 cos FN 2 cos FN 3 F 0Al3l2 A2yl1A1 A3 PFN1FN3 FN2、几何方程——变形协调方程: l1 l2 L3 cos 、物理方程-变形与受力关系l1FN1l1 E1 A1,l3FN 3l3 E3 A3、联立求解:F N 1 L1 F N 3 L 3 cos E 1 A1E 3 A3xAPFN1FN 2E1A1F cos2 2E1 A1 cos3 E3 A3; FN 3E3 A3F 2E1A1 cos3 E3 A319例 木制短柱的四角用四个 40*40*4 的等边角钢加固,角钢和木材的许用应力分别为 []1 =160 MPa 和 []2 =12 MPa,弹性模量分别为 E1=200 GPa 和 E2 =10 GPa;求许可载荷 F.解:、平衡方程:FF Y 0 4FN1 FN 2 F 01m250FN 2 4FN1、几何方程: L1 L2、力的补充方程:L FN L EAF N 1 L1 F N 2 L 2E 1 A1E 2 A2250 F N 1 0 .07 F ; F N 2 0 .72 F20 、求结构的许可载荷: max FN max AFN max A F N 1maxA1 1,角钢面积由型钢表查得:A 1=3.086 c㎡ FN 1max 3.1 16 10 3 49 .4(k N ) F N 2 max A 2 2 , F N 2 max 250 2 12 750 ( kN )F1max A1 1 / 0.07 705.4(kN )F2max A2 2 / 0.72 1042(kN) [Fmax]=705.4 kN21例: 图示结构,已知: L、A、E、a、F 。