第二章 轴向拉压变形

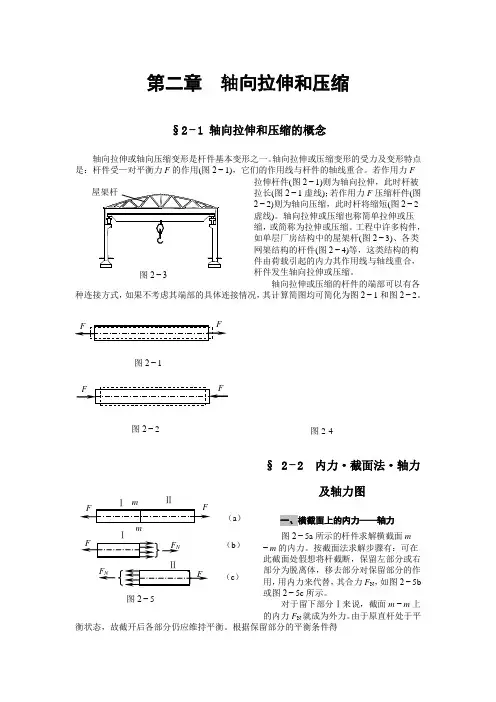
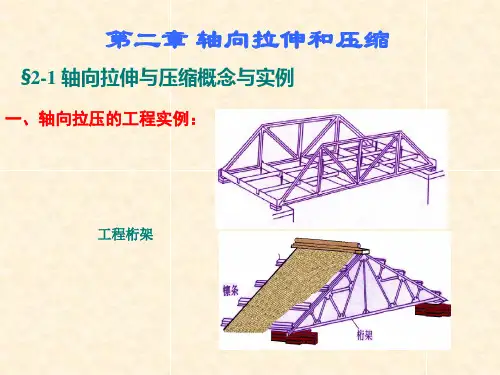
第二章 轴向拉伸和压缩§2−1 轴向拉伸和压缩的概念F(图2−1)则为轴向拉伸，此时杆被2−1虚线)；若作用力F 压缩杆件(图(图2−2工程中许多构件，(图2−3)、各类(图2−4)等，这类结构的构2−1和图2−2。

§ 2−2 内力·截面法·轴力及轴力图一、横截面上的内力——轴力图2−5a 所示的杆件求解横截面m−m 的内力。

按截面法求解步骤有：可在此截面处假想将杆截断，保留左部分或右部分为脱离体，移去部分对保留部分的作用，用内力来代替，其合力F N ，如图2−5b 或图2−5c 所示。

对于留下部分Ⅰ来说，截面m −m 上的内力F N 就成为外力。

由于原直杆处于平衡状态，故截开后各部分仍应维持平衡。

根据保留部分的平衡条件得 mF N F N（a ）（b ） （c ）图2−5Ⅱ图2−1图2−2图2-4F F F F Fx==-=∑N N ,0,0 (2−1)式中，F N 为杆件任一截面m −m 上的内力，其作用线也与杆的轴线重合，即垂直于横截面并通过其形心，故称这种内力为轴力，用符号F N 表示。

若取部分Ⅱ为脱离体，则由作用与反作用原理可知，部分Ⅱ截开面上的轴力与前述部分上的轴力数值相等而方向相反(图2−5b,c)。

同样也可以从脱离体的平衡条件来确定。

二、轴力图当杆受多个轴向外力作用时，如图2−7a ，求轴力时须分段进行，因为AB 段的轴力与BC 段的轴力不相同。

要求AB 段杆内某截面m −m 的轴力，则假想用一平面沿m −m 处将杆截开，设取左段为脱离体(图2−7b)，以F N Ⅰ代表该截面上的轴力。

于是，根据平衡条件∑F x ＝0，有 F F -=ⅠN负号表示的方向与所设的方向相反，即为压力。

要求B C 段杆内某截面n-n 的轴力，则在n −n 处将杆截开，仍取左段为脱离体（图2−7c ），以F N Ⅱ代表该截面上的轴力。

于是，根据平衡条件∑F x ＝0，有 02N Ⅱ=+-F F F由此得F F =N Ⅱ在多个力作用时，由于各段杆轴力的大小及正负号各异，所以为了形象地表明各截面轴力的变化情况，通常将其绘成“轴力图”(图2−7d)。

第
二
章
拉伸压缩与剪切
1
பைடு நூலகம்
§2-1

轴向拉伸与压缩的概念和实例
轴向拉伸——轴力作用下，杆件伸长 （简称拉伸） 轴向压缩——轴力作用下，杆件缩短 （简称压缩）

2
拉、压的特点：

1.两端受力——沿轴线，大小相等，方向相反 2. 变形—— 沿轴线
3

§2-2 轴向拉伸或压缩时横截面上的内力和应力
1 、横截面上的内力
A3
2
l1 l2 y AA3 A3 A4 sin 30 tan 30 2 1.039 3.039mm
A
A A4
AA x2 y2 0.6 2 3.039 2 3.1mm
40
目录
例 2—5 截面积为 76.36mm² 的钢索绕过无摩擦的定滑轮 F=20kN，求刚索的应力和 C点的垂直位移。 （刚索的 E =177GPa，设横梁ABCD为刚梁）
16
§2-4

材料在拉伸时的力学性能
材料的力学性能是指材料在外力的作用下表现出的变 形和破坏等方面的特性。

现在要研究材料的整个力学性能（应力 —— 应变）：
从受力很小
破坏
理论上——用简单描述复杂
工程上——为（材料组成的）构件当好医生
17
一、 低碳钢拉伸时的力学性能 （含碳量<0.3%的碳素钢）
力均匀分布于横截面上，σ等于常量。于是有：
N d A d A A
A A
得应力：

N A
F
FN
σ
10
例题2-2
A 1
45°
C
2

μ
16锰钢
合金钢 铸铁 混凝土 石灰岩 木材（顺纹）
196-216
186-216 59-162 15-35 41 10-12
0.25-0.30
0.25-0.30 0.23-0.27 0.16-0.18 0.16-0.34
橡胶
0.0078
0.47
25
材料力学
§2-5
轴向拉伸时材料的机械性能
一、试验条件及试验仪器
P BC段：N 2 3 P
1
3P + P
AB段：N
3
2 P
+
–
12
2P
三、横截面上的应力
问题提出： P P （一）应力的概念 P P
度量横截面 上分布内力 的集度
1.定义：作用在单位面积上的内力值。 2.应力的单位是： Pa KPa MPa GPa
3.应力：a：垂直截面的应力－－正应力σ 拉应力为正，压应力为负。
※E为弹性模量，是衡量材料抵抗弹 性变形能力的一个指标。“EA”称 为杆的抗拉压刚度。
l E Sl S E E l l EA A
胡克定律：
＝Eε
23
四、横向变形
d d 1 d 0
泊松比（或横向变形系数）
d d 1 d 0 相对变形： ' d0 d0
e
DE段：颈缩阶段。
• 材料的分类：根据试件断裂时的残余相对变形率将材料分类： 延伸率（δ ）>5% 塑性变形：低碳钢，铜，塑料，纤维。 延伸率（δ ）<5% 脆性变形：混凝土，石块，玻璃钢，陶瓷， 玻璃，铸铁。 • 冷作硬化：材料经过屈服而进入强化阶段后卸载，再加载时，弹 性极限明显增加，弹性范围明显扩大，承载能力增大的现象。 • 强度指标：对塑性材料，在拉断之前在残余变形0.2 %（产生 0.2%塑性应变）时对应的应力为这种材料的名义屈服应力，用 0.2表示 ，即此类材料的失效应力。 锰钢、镍钢、铜等 • 脆性材料拉伸的机械性能特点： 1.断裂残余相对变形率δ <5% 0.2 or s max b 2.弹性变形基本延伸到破坏 3.拉伸强度极限比塑性材料小的多 4.b是脆性材料唯一的强度指标

明德行远 交通天下
材料力学
2. 轴力的正负规定 FN 与外法线同向,为正轴力(拉力)
FN
FN F N > 0
FN与外法线反向,为负轴力(压力)
FN
FN
二、轴力图--表明构件不同截面轴力的变化规律
意 ①反映出轴力与截面位置变化关系，较直观； 义 ②确定最大轴力的数值及其所在横截面的位置，
即确定危险截面位置，为强度计算提供依据。
斜截面外法线方向为正，反之为负。
明德行远 交通天下
材料力学
a pa cosa cos2 a
pa
a
pa
sin a
cosa sin a
1
2
sin 2a
讨 论：
当a = 0°时， (a )max (横截面上正应力最大)
当a = 90°时，
( a )min 0
当a
=
±
45°时，| a
|max
2
结果表明，杆件的最大工作应力在BC段，其值为0.75MPa。
明德行远 交通天下
材料力学
二、斜截面上的应力
k
F
F
设有一等直杆受拉力F作用，横截面面积为A。
求：斜截面k-k上的应力。
F
αk
Fα
解：截面法求内力。由平衡方程：
Fa=F
F
则：pa
Fa Aa
Aa：斜截面面积；Fa：斜截面上内力。
由几何关系：
A
材料力学
第二章 轴向拉伸和压缩
明德行远 交通天下
材料力学
主要内容
• §2-1 轴向拉伸与压缩的概念 • §2-2 轴力及轴力图 • §2-3 应力 • §2-4 轴向拉伸或压缩杆件的变形及节点位移 • §2-5 材料拉伸和压缩时的力学性能 • §2-6 轴向拉伸和压缩杆件的强度计算 • §2-7 轴向拉（压）杆的超静定问题

拉压杆斜截面上的应力Ｐ
Ａ为横截面的面积 Ａ为斜截面的面积 横截面上的正应力 斜截面上的应力
N p A P P cos cos A A cos
P A
斜截面上的正应力和剪应力
p cos cos2 p sin cos sin
P
1 1 P A N1 3P C 2 N2
A
∴N2=P－3P= －2P
2
3、内力图
P A l P
3P
B
注意：
1 、一次只能取一个截面， 将原构件分成两部分。
C
l
Ｎ
O
2、内力方向设为正向后建立平 衡方程求解。（说明＋－）
3 、分离体图与原图上下对 齐，截面位置一目了然。 4 、轴力图大小近似按比例， 也要与上图对齐。 练习：
1、变形规律试验及平面假设：
a c
P
b d
变形前
a´ c´
b´ d´
受力后 P
2、变形规律： 横向线——仍为平行的直线，且间距增大。 纵向线——仍为平行的直线，且间距减小。 平面假设：原为平面的横截面在变形后仍为平面. N 3、横截面上的应力：均匀分布 A
例２-４：计算下图中指定截面上的应力。ＡＢ段与ＣＤ段的横截面积均 为２０mm2，ＡＢ段横截面积为 1０ mm2 ，
C
已知：三角架 ABC 的〔σ 〕=120 MPa，AB 杆为 2 根 80*80*7 的等边角钢，AC 为 2 根 10 号槽钢，AB、AC 两杆的夹角为300 。 求：此结构所能承担的最大外荷载 Fmax
解： 1、F 与 FN 的关系
Y
0
X 0 F Y 0 F
NAC
FNAB cos30 0

伸长 l2 0.24mm 缩短
2、计算各杆轴向变形
C
l 2 =1m a =170mm
B'
B2
F
l1 0.48mm
3、由变形的几何条件确定B点的位移 分别以A为圆心，AB1为半径，C为圆 心，CB1为半径画弧，相较于B’点，
B"
小变形条件，可以用切线代替弧线。
材料力学
第2章 轴向拉伸和压缩
FN FN ( x)
轴力方程
即为轴力图。
即：FN随x的变化规律
以x为横坐标，以FN为纵坐标，绘制FN F（ ）的关系图线， N x
FN
正的轴力画在x轴的上侧，负的画在下侧.
x
材料力学
第2章 轴向拉伸和压缩
例题1
等值杆受力如图所示，试作其轴力图
F =25kN F ４=55kN ４ １=40kN F
纵向线 即： 原长相同
变形相同
横截面上各点的纵向线应变相等
c
拉压杆变形几何方程.
反映了截面上各点变形之间的几何关系.
材料力学
第2章 轴向拉伸和压缩
§2-2 横截面上的正应力 应力分布规律 找变形规律 研究思路： 试验观察 综合几何方面、物理方面、静力学方面推导应力计算公式
一、几何方面
F
a' b'
材料力学
第2章 轴向拉伸和压缩
第二章 轴向拉伸和压缩
材料力学
第2章 轴向拉伸和压缩
• • • • • •
本章主要内容 轴力及轴力图 横截面上的应力 拉压杆的变形、胡克定律 强度计算 材料的力学性质
材料力学
第2章 轴向拉伸和压缩
§2-1 概述 一、工程实际中的轴向拉压杆

2 sin ( 2 cos 1 )ctg 3.9 103 m
B1 B B1 B3 B3 B
B B
B B12 B1 B 2 4.45 10 3 m
[例2-11] 薄壁管壁厚为,求壁厚变化和直径变化D。
解：1）求横截面上的正应力
dx
N ( x) l dx EA( x) l
例[2-4] 图示杆，1段为直径 d1=20mm的圆杆，2 段为边长a=25mm的方杆，3段为直径d3=12mm的圆杆。 已知2段杆内的应力σ 2=-30MPa，E=210GPa，求整个 杆的伸长△L
解: P 2 A2
30 25 18.75KN
N 1l Pl l1 l2 EA 2 EA cos l1 Pl cos 2 EA
[例2-8]求图示结构结点A 的垂直位移和水平位移。
解:
N1 P, N 2 0
Pl l1 , l2 0 EA Pl y l1 EA
N1
N2
Pl x l1ctg ctg EA
F
FN
FN F
F
F
CL2TU2
2.实验现象：
平截面假设
截面变形前后一直保持为平面，两个平行的截面之 间的纤维伸长相同。 3.平面假设：变形前为平面的横截面变形后仍为平面。 4.应力的计算 轴力垂直于横截面，所以其应力也仅仅是正应力。按 胡克定律：变形与力成正比。同一截面上各点变形相 同，其应力必然也相同。 FN （2-1） A 式中： A横截面的面积；FN该截面的轴力。 应力的符号：拉应力为正值应力，压缩应力为负 值应力。
1. 截面法的三个步骤 切: 代: 平:
F F F F

拉伸—拉力，其轴力为正值。方向背离所在截面。 压缩—压力，其轴力为负值。方向指向所在截面。
F
N （＋） N
F
F
N （－） N
F
轴力一般按正方向假设。
3、轴力图： 轴力沿轴线变化的图形
F
F
N
4、轴力图的意义
+ x
① 直观反映轴力与截面位置变化关系；
② 确定出最大轴力的数值及其所在位置，即确定危险截面位置，为 强度计算提供依据。
1、低碳钢轴向拉伸时的力学性质 (四个阶段)
⑴、弹性阶段:OA
OA’为直线段； E
AA’为微弯曲线段。
p —比例极限； e —弹性极限。
一般这两个极限相差不大， 在工程上难以区分，统称为弹 性极限
低碳钢拉伸时的四个阶段
⑴、弹性阶段:OA, ⑵、屈服阶段:B’C。
s —屈服极限
屈服段内最低的应力值。
例 图示杆的A、B、C、D点分别作用着大小为FA = 5 F、 FB = 8 F、 FC = 4 F FD= F 的力，方向如图，试求各段内力并画出杆的轴力图。
OA
BC
D
FA
FB
FC
FD
N1
A
BC
D
FA
FB
FC
FD
解： 求OA段内力N1：设截面如图
X 0 FD FC FB FA N1 0
N4= F
FD
N1 2F , N2= –3F， N3= 5F， N4= F
N1 2F , N2= –3F， N3= 5F， N4= F
轴力图如下图示
OA
BC
D
FA
FB
FC
FD
N 2F
5F

危险点：应力最大的点。
s
max
max(
FN ( x) A( x)
)
16
4. 公式的应用条件： 直杆、杆的截面无突变、截面到载荷作用点有一定 的距离。
5. Saint-Venant原理： 离开载荷作用处一定距离，应力分布与大小不受外载荷作
用方式的影响。 6. 应力集中（Stress Concentration）： 在截面尺寸突变处，应力急剧变大。
10
轴力图的特点：突变值 = 集中载荷 轴力(图)的简便求法： 自左向右:
遇到向左的P， 轴力N 增量为正； 遇到向右的P ， 轴力N 增量为负。
8kN
5kN
3kN
5kN +
5kN
8kN – -3kN
8kN 3kN
11
简
OA
便
求
5P
法
OA
RO=2P
5P
FN
2P +
–
- -3P
PD = P, 轴力图如何？ FN
3
力学模型如图
P
轴向拉伸，对应的力称为拉力。
P
轴向压缩，对应的力称为压力。
P P
4
二、
工 程 实 例
5
§2–2 内力、截面法、轴力及轴力图
例如： 截面法求FN
P
A
P
截开：
P
A P
简图
代替：
P
FN A
平衡：
X 0 P FN 0 P FN
2. 轴力——轴向拉压杆的内力，用FN 表示。
6
3. 轴力的正负规定: FN 与外法线同向,为正轴力(拉力) FN
0
–
-5P
BC 8P 4P

σ
F FN
σ =
FN A
拉应力为正 压应力为负
拉压杆横截面上正应力计算公式
公式适用于轴载作用的杆件。 公式适用于轴载作用的杆件。 变截面杆或分布轴载作 用下横截面正应力计算
σ ( x) =
FN ( x ) A( x )
2.2 拉压杆的应力
二、斜截面上的应力
σ F σ
τ= σ
σ
2
σ
τ=
2
σ
F
2 σ τ= 2
ρgπ
l
ξ )2
叠加原理适用
FN (0) = F
FN (l ) = ( F + P)
dFN ( x) ρgπ 2 d1 (d 2 d1 ) d d ρgπ d d = [d1 + 2 x + ( 2 1 )2 x2 ] = (d1 + 2 1 x) 2 = p( x) dx 4 l l 4 l
单向(单轴) 单向(单轴)应力状态
σ
2
σ τ = 2 σ
2
2
讨论任一方位截面上的应力及与横截面上应 作顺时针转动的趋势为正。 切应力以使隔离体有作顺时针转动的趋势为正。 力的关系， 力的关系，斜截面上各处法向线应变和切应 σ max = σ 0 = σ τ0 = 0 横截面上 变相同，即变形是均匀的。 变相同，即变形是均匀的。因此内力均匀分 σ min = σ 90 = 0 τ 90 = 0 布。 纵截面上 σ Fα = ∫ Aoα p α dAτ max p ατ ∫ Aα=dA = p α σ α = σ = = A F
2.1 拉压杆的内力 轴力及轴力图
横截面是杆件内最有代表性的截面， 横截面是杆件内最有代表性的截面， 其上的内力可用截面法求出。 其上的内力可用截面法求出。 由隔离体的平衡条件截面上只 有截面法向的内力分量 FN(x), ), 轴力。 称为轴力 称为轴力。 由 ∑ Fx = FN ( x) F = 0

第二章轴向拉(压变形[习题2-1]试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

（a）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（b）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（c）解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（d）解：（1）求指定截面上的轴力（2）作轴力图中间段的轴力方程为：轴力图如图所示。

[习题2-2]试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，试求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。

若横截面面积，，，并求各横截面上的应力。

解：（1）求指定截面上的轴力（2）作轴力图轴力图如图所示。

（3）计算各截面上的应力[习题2-4] 图示一混合屋架结构的计算简图。

屋架的上弦用钢筋混凝土制成。

下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个的等边角钢。

已知屋面承受集度为的竖直均布荷载。

试求拉杆AE和EC横截面上的应力。

解：（1）求支座反力由结构的对称性可知：（2）求AE和EG杆的轴力①用假想的垂直截面把C铰和EG杆同时切断，取左部分为研究对象，其受力图如图所示。

由平衡条件可知：②以C节点为研究对象，其受力图如图所示。

由平平衡条件可得：（3）求拉杆AE和EG横截面上的应力查型钢表得单个等边角钢的面积为：[习题2-5] 石砌桥墩的墩身高，其横截面面尺寸如图所示。

荷载，材料的密度，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：墩身底面积：因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

[习题2-6]图示拉杆承受轴向拉力，杆的横截面面积。

如以表示斜截面与横截面的夹角，试求当时各斜截面上的正应力和切应力，并用图表示其方向。

解：斜截面上的正应力与切应力的公式为：式中，，把的数值代入以上二式得：轴向拉/压杆斜截面上的应力计算题目编号10000 100 0 100 100.0 0.0 习题2-6100 30 100 75.0 43.310000100 45 100 50.0 50.010000100 60 100 25.0 43.310000100 90 100 0.0 0.010000[习题2-7]一根等直杆受力如图所示。

第二章 轴向拉伸和压缩
拉、压杆件的变形分析
解：1． 作轴力图 由于直杆上作用有4个轴向 载荷，而且AB段与BC段杆横截 面面积不相等，为了确定直杆 横截面上的最大正应力和杆的 总变形量，必须首先确定各段 杆的横截面上的轴力。
应用截面法，可以确定AD、 DEB、BC段杆横截面上的轴力 分别为：
FNAD＝－2FP＝ －120 kN； FNDE＝FNEB＝－FP＝ －60 kN； FNBC＝FP＝60 kN。
F

K
p
A
(a)
K
(b)
ΔF p ΔA
(1)应力定义在截面内的一点处； (2)应力是一个矢量。 正应力, 切应力
ΔF dF p lim Δ A 0 Δ A dA
单位：Pa (N/m2)， MPa (106 N/m2)
第二章 轴向拉伸和压缩 上节回顾 轴向拉伸和压缩杆件横截面上只有正应力。
A A ＝ cos
FP x＝ A
其中，x为杆横截面上的正应力; Aθ 为斜截面面积
第二章 轴向拉伸和压缩 上节回顾
＝ x cos
2
1 ＝ xsin 2 2
由于微元取得很小，上述微元斜面上的应力， 实际上就是过一点处不同方向面的应力。因此，当 论及应力时，必须指明是哪一点处、哪一个方向面 上的应力。
第二章 轴向拉伸和压缩
拉、压杆件的变形分析
绝对变形
弹性模量
FPl FN l Δl EA EA
当拉、压杆有二个以上的外力作用时，需要 先画出轴力图，然后按上式分段计算各段的变形， 各段变形的代数和即为杆的总伸长量(或缩短量)：
FNi li Δ l i EAi
第二章 轴向拉伸和压缩

第二章轴向拉伸和压缩§2-1 引言此类受轴向外力作用的等截面直杆称为拉杆或压杆。

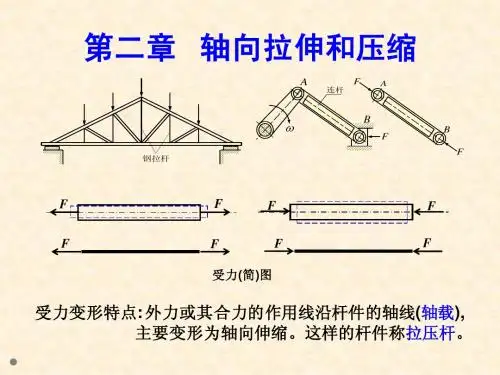
受力特点：直杆受到一对大小相等，作用线与其轴线重合的外力F 作用。

变形特点：杆件发生纵向伸长或缩短。

F F F F 一、轴向拉压杆的受力特点、变形特点二、轴力及轴力图Ⅰ、内力内力——由于物体受外力作用而引起的其内部各质点间相互作用的力的改变量。

F F F F根据可变形固体的连续性假设可知，物体内部相邻部分之间的作用力是一个连续分布的内力系，我们所说的内力是该内力系的合成（力或力偶）求内力的一般方法——截面法（1）截开；（2）代替；（3）平衡。

步骤： FFmm (c) F N (a) FF m m (b) m m F N x 二、轴力及轴力图Ⅰ、内力---轴力可看出：杆件任一横截面上的内力，其作用线均与杆件的轴线重合，因而称之为轴力，用记号F N 表示。

F F +=N FF mm (c)F N (a) FF m m (b) m m F N x引起伸长变形的轴力为正——拉力（背离截面）；引起压缩变形的轴力为负——压力（指向截面）。

轴力的符号规定:F F +=N FF mm (c)F N (a) FF m m (b) m m F N xFF -=N F N mm(c) F N (a) FF m m (b) mm F x F若用平行于杆轴线的坐标表示横截面的位置，用垂直于杆轴线的坐标表示横截面上轴力的数值，所绘出的图线可以表明轴力与截面位置的关系，称为轴力图。

FF F N 图F F FF N 图F注意：用截面法法求内力的过程中，在截面取分离体前，作用于物体上的外力（荷载）不能任意移动或用静力等效的相当力系替代。

F F(a)F F(b)F N =Fmmnn (a)FCB Am mFA(b)F N =Fnn B FA(c)n n mmF N =0(e)mmAF N =Fn n B(f)AFCB(d)F A例试作图示杆的轴力图。

第二章 轴向拉伸和压缩
§1 轴向拉伸与压缩的概念
拉伸
压缩
受力特征：外力合力的作用线与杆件的轴线重合 变形特征：轴向伸长或缩短
§2 内力、截面法、轴力及轴力图
1、内力的概念
固有内力：分子内力.它是由构成物体的材料的物理性质所决
定的.(物体在受到外力之前，内部就存在着内力)
附加内力：在原有内力的基础上，又添加了新的内力
以AB杆为研究对象
mA 0
FNFBNCBC 9101k8N 5 0
以CDE为研究对象
mE 0
FNCD 40kN
20kN 18kN 4m
FNCD sin 300 8 FNBC 8 20 4 0
30O FNCD C
FNBC
B 4m
BC
FNBC ABC
CD
FNCD ACD
书中例题
注意：1.轴力是杆横截面上分布内力系的合力，其作用线也与杆件的轴
线重合，所以称为轴力。 2.静力学中的力或力偶的可传性原理，在用截面法求内力的过程
中是有限制的。
内力的正负号规则
同一位置处左、右侧截面上内力分量必须具有相 同的正负号。
FN
FN
FN
FN
FN
FN
拉力为“正” 压力为“负”
例题 2.1
2.12
2.1×105MPa，设在结点A处悬挂一重物F＝100kN，试求
结点A的位移δA。
X 0
FNAC
FNAB
F
2 cos
FNAC sin FNAB sin 0
B1
2 C
Y 0 FNAC cos FNAB cos F 0
FNAB FNAC
αα
DLAB

2.5.5 塑性材料和脆性材料的主要区别
(5) 塑性材料承受动载荷的能力强，脆性材料承 受动荷载的能力很差，所以承受动载荷作用的构 件多由塑性材料制做。
2.5.5 塑性材料和脆性材料的主要区别
对于脆性材料，当应力达到其强度极限σb 时， 构件会断裂而破坏；对于塑性材料，当应力达到 屈服极限σs时，将产生显著的塑性变形，常会 使构件不能正常工作。
2.5.2 低碳钢拉伸时的力学性能
OB:弹性阶段__弹性极限σe BC:屈服阶段__屈服极限σs CD:强化阶段__强度极限σb DE:颈缩阶段
2.5.2 低碳钢拉伸时的力学性能
OB:弹性阶段---弹性极限σe OA:线性阶段---比例极限σP
σ=Eε 胡克定律
E: 弹性模量 σe≈σP
伸长率
Fbs
Fbs
Fbs
实际挤压面
挤压应力：
2.8.2 挤压和挤压强度计算
smaxBiblioteka dFbs(a)
smax
(b)
t
(b)
ssj bs
(c) (c)
挤压面 计算挤压面积 =dt
两种材料的极限应力分别是？ 许用应力=？
2.6 拉压杆的变形
2.6 拉压杆的变形
例： 已知等截面直杆横截面面积A＝500mm2,弹性模量 E＝200GPa，试计算杆件总变形量。
6KN
8KN 5KN
3KN
1m
2m
1.5m
ΔL=？
2.8 拉压杆接头的计算
2.8 拉压杆接头的计算
2.8.1 剪切和剪切强度计算
(1) 多数塑性材料在弹性变形范围内，应力与应 变成正比关系，符合胡克定律；多数脆性材料在 拉伸或压缩时σ-ε图一开始就是一条微弯曲线， 即应力与应变不成正比关系，不符合胡克定律， 但由于σ-ε曲线的曲率较小，所以在应用上假设 它们成正比关系。

第二章 轴向拉伸与压缩
§2-1 轴向拉伸与压缩概念 §2-2 轴向拉压时横截面上的内力与应力 §2-3 直杆轴向拉压时斜截面上的应力
§2-1 轴向拉伸与压缩的概念和实例
1、轴向拉压的受力特点： 外力的合力作用线与杆的轴线重合。
2、轴向拉压的变形特点：
轴向拉伸： 轴向伸长，横向缩短。 轴向压缩： 轴向缩短，横向变粗。 3、力学模型


p
sin
s
cos
sin

1s
2
sin 2
s的正负号: 拉应力为正，压应力为负。 的正负号: 绕所保留的截面， 顺时针为正，
逆时针为负。
四、sα 、α出现最大的截面
1、=0º即横截面上，s达到最大
s s cos 2 s
0
2、=45º的斜截面上， 剪应力达最大
A
PA FN2
B
PB B
PB FN3
C
PC C
PC C
PC FN4
FN 2P
5P P
-3P
D PD
D PD
D PD D
PD
x
★轴力图的特点：
1）遇到集中力，轴力图发生突变； 2）突变值 = 集中载荷的大小
★轴力(图)的突变规律：
1）遇到向左的P， 轴力FN 向正方向突变;
自左向右: 2）遇到向右的P ， 轴力FN 向负方向突变；
FN
FN
FN>0
N 与外法线同向,为正轴力(拉力)-
--产生拉伸变形内力为正;
FN
FN
FN<0
N与外法线反向,为负轴力(压力)--
-产生压缩变形内力为负.
4、 轴力图—— FN (x) ~x 的图象表示

起重机的吊缆
A
B
图2-1-1
桁架中的杆件
曲柄连杆机构 特点： 连杆为直杆 外力大小相等 方向相反 沿杆轴线 杆的变形为轴向伸长或缩短
连杆
ω
F
以轴向伸长或轴向缩短为主要特征的变形形式称 为轴向拉伸或轴向压缩。
F
F
F
F
（1）受力特征: 构件是直杆；作用于杆件上的外力或外力合力
的作用线沿杆件的轴线。
FN A s 3780 10 3 90 42 103 mm2
FN s s A
(3)求尺寸h、b
A hb 1.4b 2
A 42 103 b 173mm 1.4 1.4
h 1.4b 1.4 173 245mm
故取h 245mm ，b 173mm 。
C
FN1 1m A FN2 F
B 解： (1)求轴力
A F
F 0 F F cos 30 0 x N2 N1
FN 1 2F FN 2 3F
F
y
0 FN 1 sin 30 F 0
AB杆—10号工字钢， AC杆—80mm80mm7mm等 边角钢， [s]=170MPa。试确定结构的许可载荷[F]。 FN1 FN 1 2F (2)确定两杆的面积 FN 2 3F 查表得：A1 10.86 2 21.72cm2 A 2 14.34 2 28.68cm2 A FN2 (3)确定许可载荷[F] F 由AB杆确定： 由AC杆确定： FN 2
（4）结论: 横截面上只有正应力，并均匀分布，用s 表示。 2、正应力计算公式
F FN
轴力与应力的关系： FN A s d A sA