2010年暑期数学建模作业一 2

摘要本文属于输油管布置最优化问题，建立了数形结合的方法，建立铺设管道费用最省的最优化模型。

问题一建立直角坐标系，利用线性规划知识建立了通用的一般模型：建立直角坐标系设A ()11,y x 、B ()22,y x 两点为炼油厂位置，设一点O ()y x ,，两炼油厂在此点（42)433(212222--+---+--k xky k x ky y x bb bb a b ，42212121---+kx k y y b a b ）时，铺设共用管道费用最省，用Maple 软件编程求解此点。

问题二进一步加深模型难度，引入城镇与郊区不同情形以及城镇中拆迁附加费用，模型运用lingo 软件进行求解，得出了管线铺设费用最省的最优值280.332万元；问题三将铺设A 、B 、共用管道费用一一列出，拆迁附加费用同上，并且数值赋予此模型，依问题二模型求得铺设管道费用最省时的费用250.012万元 。

关键词： 数形结合 、直角坐标系 、Maple 软件 、 最优化模型一、问题重述某油田计划在铁路线一侧建造两家炼油厂，同时在铁路线上增建一个车站，用来运送成品油。

论文在问题一中阐述了针对两炼油厂到铁路线距离和两炼油厂间距离的各种不同情形，设计不同方案，列出了若有共用管道时，共用管道与非共用管道费用差异带来的不同情况；论文在问题二中阐述了一更为复杂的情形进行具体的设计方案，两炼油厂的具体位置在已知图上已经给出，其中A厂位于郊区（图中的I区域），B厂位于城区（图中的II区域），所有管线的铺设费用均为每千米7.2万元，而且题基础上扩展，要求给出管线布置方案及建立最省的相应费用模型；论文在问题三中阐述了更实际的问题，为进一步节省费用，可以根据炼油厂的生产能力，选用相适应的油管。

这时的管线铺设费用将分别降为输送A厂成品油的每千米5.6万元，输送B厂成品油的每千米6.0万元，共用管线费用为每千米7.2万元。

问题讨论的更加符合实际，要求建立的模型更贴近现实。

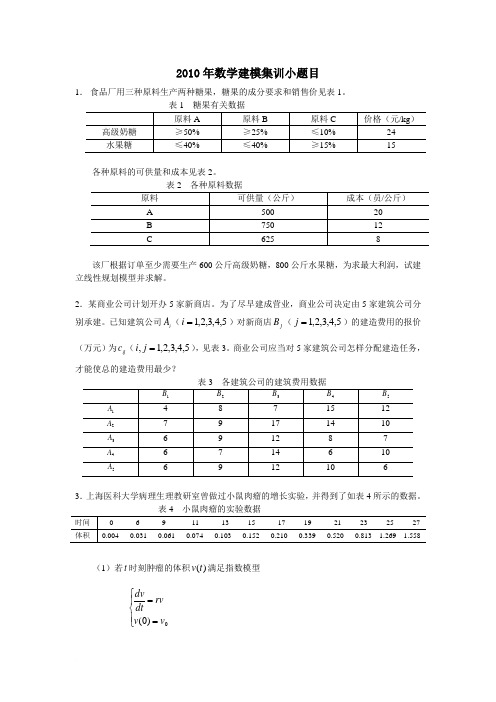
2010年数学建模集训小题目1． 食品厂用三种原料生产两种糖果，糖果的成分要求和销售价见表1。

表1 糖果有关数据各种原料的可供量和成本见表2。

该厂根据订单至少需要生产600公斤高级奶糖，800公斤水果糖，为求最大利润，试建立线性规划模型并求解。

2．某商业公司计划开办5家新商店。

为了尽早建成营业，商业公司决定由5家建筑公司分别承建。

已知建筑公司i A （5,4,3,2,1=i ）对新商店j B （5,4,3,2,1=j ）的建造费用的报价（万元）为ij c （5,4,3,2,1,=j i ），见表3。

商业公司应当对5家建筑公司怎样分配建造任务，才能使总的建造费用最少？3．上海医科大学病理生理教研室曾做过小鼠肉瘤的增长实验，并得到了如表4所示的数据。

（1）若t 时刻肿瘤的体积)(t v 满足指数模型⎪⎩⎪⎨⎧==0)0(v v rvdtdv请拟合参数r 。

（2）若t 时刻肿瘤的体积)(t v 满足Logistic 模型⎪⎩⎪⎨⎧=-=02)0(v v vv dtdv βα 请拟合参数βα,。

4．已知数据见表5。

试求y 对321,,x x x 的线性回归方程并检验回归效果，能否剔除一个变量？5．炼钢厂出钢时所用的盛钢水的钢包，由于钢水对耐火材料的侵蚀作用，随着使用次数的增加，容积不断增大，实测得到15组数据如表6。

试分别按以下两种形式建立y 对x 的回归方程，画出散点图和回归曲线，并根据适当的指标判断哪一种好。

（1）xb a y +=1； （2）xbce y =.6．已知数据见表7。

试求形式为x a x a x a a y sin 332210+++=的回归方程并检验回归效果。

7．一枚导弹，以初始速度0v ，水平夹角α离开原点)0,0(。

如果导弹在),(e e y x 点着陆，且在飞行中受到一拉力，其大小和速度的平方成比例，那么控制导弹飞行轨迹的四个一阶方程为⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==++-=+-=x xy x yx y d y y x d x vdx dt vv dx dy v v v v c g dxdv v v c dx dv 12222 其中y 是导弹的垂直高度，x 是飞行的水平距离，t 是时间，x v 和y v 分别是速度v 的水平和垂直分量，d c 是拉力系数，g 是重力加速度。

数学学院2010级研究生《数学模型方法》试题说明：以下共六道建模题，1）、2）两题可任选一题，5）、6）两题可任选一题，3）、4）题必做，请同学们每人独立完成四道题，严禁雷同。

1． 在大洋上航行的一只游船上有800人，一名游客患了某种传染病，12小时后有3人发病。

由于这种传染病没有早期症状，故感染者不能被及时隔离。

直升机将在60至72小时运来疫苗。

()1试估算疫苗运到时患此传染病的人数。

()2试推算传染病高潮到来的时刻。

()3若初始时刻的患病人数为0I 即()00I I =,应如何修正你的模型。

2．单课树木的商品价值V 是由这棵树所能够生产的木材体积和质量所决定的。

显然， V=V （t ）依赖于树木的年龄。

假设贴现率为r 。

1） 假设曲线V(t)已知，C 为树木砍伐成本。

试给出砍伐树木（更确切地说，砍伐相同年龄的树木）的最优年龄。

2） 如果考虑到森林轮种问题，即一旦树木从某一处砍掉，这块土地便可以种植新树，假定各轮种周期具有相同的长度，试讨论最优砍伐轮种的森林管理策略。

3） 已知英属哥伦比亚Douglas 松树的净立木价值V(t ）—C 随着树龄变化的资料如下：讨论Douglas 松的最优砍伐轮种问题。

3. 设备更新问题：企业使用一台设备，每年年初，企业领导就要确定是购置新的，还是继续使用旧的。

若购置新设备，就要支付一定的购置费用，已知该种设备在每年年初的价格如表35-所示；若继续使用，则需支付一定的维修费用，使用不同时间设备所需维修费如表1所示。

现要制定一个五年之内的设备更新计划，使得五年内的总的支付费用最少。

表1 设备在每年年初的价格第一年 第二年 第三年 第四年 第五年 1111121213表45- 使用不同时间设备所需维修费使用年限 0~1 1~2 2~3 3~4 4~5 维修费 56811184. 某电力公司经营两座发电站，发电站分别位于两个水库上，位置如下图所示。

已知发电站可以将水库A 的1万3m 的水转换为400千度电能，发电站B 只能将水库B 的1万3m 的水转换为200千度电能。

华中科技大学《数学建模》考试卷（半开卷）2010～2011学年度第一学期成绩学号专业班级姓名一、怎样解决下面的实际问题，包括需要哪些数据资料，要作些什么观察、试验以及建立什么样的数学模型等。

（10分）（1）估计一批电饭煲的寿命；（2）一高层办公楼有四部电梯，早晨上班时间非常拥挤，试制订合理的运行计划。

解：（1）从一批电饭煲中取一定数量的样本，测得其平均寿命，可作为该批电饭煲寿命的估计值。

为衡量估计的精度，需要从样本寿命确定该批电饭煲寿命的概率分布，即可得到估计值的置信区间。

还可试验用提高电压的办法加速寿命测试，以缩短测量时间。

⑤（2）统计在各层上班的人数，通过数据或计算确定电梯运行时间，以等待的人数与时间乘积为目标，建立优化模型，确定每部电梯运行的楼层（有的从大厅直接运行到高层）。

⑤二、学校共有1000名学生，235人住在A 宿舍，333人住在B 宿舍，432人住在C 宿舍。

学生们要组织一个10人的委员会，试用以下方法分别分配各宿舍的委员数。

（10分） 1.Hamilton 方法 2.Q 值方法3.其它方法或你自己提出的方法解：1.Hamilton 方法:③2.Q 值法: 先按比例计算结果将整数部分的9席分配，123n 2,n 3,n 4=== ①再用Q 值法分配第十席：()()()()()()221111222222223333p 235Q 9204.17n n 1221p 333Q 9240.75n n 1331p 432Q 9331.20n n 1441===++===++===++ ③Q 3最大，第十席分配给C 宿舍，即：123n 2,n 3,n 5===。

①3.略 ②三、人体注射葡萄糖溶液时，血液中葡萄糖浓度g (t )的增长率与注射速率r 成正比，与人体血液容积V 成反比，而由于人体组织的吸收作用，g (t )的减少率与g (t )本身成正比。

分别在以下假设下建立模型，并讨论稳定情况。

基于三角函数形式的生物节律现象模型学校：同济大学作者：金杰沈煜崔志杰基于三角函数形式的生物节律现象模型摘要在自然界中，生命体或者人工智能系统存在周期性的节律现象，而由于内外因素的作用，振幅与周期会产生相应的变化。

基于以上现象，我们利用余弦函数进行拟合，并设三角函数中的周期与振幅会随着时间而发生变化，以此来解释自然界中的这些规律。

在第一种情况(节律变快了，但是振幅变化不太大)中，假定余弦函数中的角频率会随时间而变化，而振幅为一常值，所得函数通过Matlab仿真，图像符合此类现象。

在第二种情况（振幅变化很大，但是节律相对稳定）中，假定此函数为两个具有相同角频率的余弦函数的叠加，其中角频率为常数，一个余弦函数的振幅为常数，另一个余弦函数的振幅随时间变化，所得函数经过Matlab仿真，与现象相符。

在第三种情况（振幅、周期都会有较大的变化）中，我们认为此情况为第一、二种情况的复合，所以我们将第一、二种情况所得函数进行叠加，利用Matlab仿真，符合第三种情况。

为了验证所得函数是否符合实际情况，我们分别对心率生理调节机制模型与血糖反馈调节机制模型进行求解。

对于第一个模型，根据资料我们认为其满足第一种情况，并考虑在剧烈运动后心脏的跳动情况。

我们将第一种情况中所得的函数对心跳情况进行模拟，调整函数中的参数，利用Matlab对函数进行仿真，将图像与实际情况相比对，得出了函数符合实际的结论。

对于第二个模型，由文献可知其符合第二种情况，我们考虑在某一时刻对人体注射大量葡萄糖后血糖浓度的曲线。

我们用第二类情况所得函数进行拟合，通过求解微分方程，我们得到了振幅随时间变化的函数，通过参数的调整，进行Matlab仿真，图像与资料中的图像基本吻合。

由此，我们认为所构造函数具有一定的实际意义。

关键词：节律现象反馈调节血糖心率周期余弦函数 MATLAB仿真问题重述大量研究资料表明，生物界广泛存在着多种与时间有关的生物节律，以此研究内容的时间生物学(Chronobiology)近年已形成一门新的独立学科。

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。

如有违反竞赛规则的行为，我们将受到严肃处理。

我们参赛选择的题号是（从A/B/C/D中选择一项填写）： C我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：浙江工贸职业技术学院参赛队员(打印并签名) ：1. 宋舒翔2. 戴慧娇3. 林伟伟指导教师或指导教师组负责人(打印并签名)：刘维先日期： 2010年 9 月 13日赛区评阅编号（由赛区组委会评阅前进行编号）：编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：赛区评阅记录（可供赛区评阅时使用）：评阅人评分备注全国统一编号（由赛区组委会送交全国前编号）：全国评阅编号（由全国组委会评阅前进行编号）：输油管的布置摘要对于问题一，本文考虑了公用管线费用与非公用管线费用相同或不同情形的因素来设计建立管线建设费用最省。

由对于问题二，本文考虑了注册资金，技术人员，负责人工作年限以及专职专业技术经济职员四个因素来评价管线费用最优解的管线布置，并利用层次分析法确定了各因素的权重，并用matlab软件编程，求的各因素的权重系数，最终计算出管线费用的最优化解F 282.8197。

m in对于问题三，在问题一和问题二的情况下，根据题目的约束条件，建立线性规划模型，由LINGO求解，得最优解F=252.0913。

m in关键词：费尔马点层次分析法二次平均最优方案1.问题重述与分析随着社会的发展，石油管道输送的优势越来越明显，管道设计的任务也越来越繁重，制定出最优的石油管道输送线，具有十分重要的经济和战略意义。

建模作业：1、大饺子能包馅。

2、追逐问题四个人甲、乙、丙、丁分别位于边长为10米的正方形ABCD的四个顶点处。

在某一时刻，四人同时出发以匀速v按顺时针方向跑向下一个人。

在进行过程中，如果他们始终保持对准目标，问他们的追逐路线是怎样的？试用计算机画出追逐过程中每个人的行进轨迹。

3、沙漠行车问题：A，B两地相距1000km，一辆汽车从A驶向B，但它一次最多装500km的汽油，因此，需要在两地之间建立加油站，问怎样建才能使总用油量最少？4、道路选择问题：我校到新校区有多条路可选择，其中一条是走快路（校东大门~右转上桥~津滨大道~快速中环~黑牛城道~宾西立交桥~宾水道~工大新校区），总长25公里，路上将遇到4个红灯，路上平均速度70公里每小时，另一条（校东大门~右转上桥~琼州道~广东道~宾水西道~工大新校区），将遇到20个红绿灯，路上均速40公里每小时，总路程18公里。

查阅相关数据，做出适当假设，将问题简化，建立模型，确定最优路线（包括时间、耗油等）。

5、编程实现1）Dijkstra最短路算法；2）Fleury求欧拉环游算法；3）求货郎担问题的改良圈算法；4）BFS求生成树算法；5）Kruskal求最小生成树算法；6）DFS纵深搜索法；7）匈牙利算法；8）人、羊、狼、菜过河问题的计算机编程实现。

每人选3个算法。

6、编程模拟卫星发射。

7、编程模拟鸭子浮水。

8、在高速公路上，常常遇到大型车超车影响小车撤诉，从而使整个公路堵塞，但是，若建成双向6车道，则会有效避免这种情况的发生，假设高速公路上有2类车：时速90-130，和时速60-80，请你查阅相关数据，建立数学模型，对高速路建成双向4车道还是双向6车道提出你的建议；并给出车速提高情况、运量变化带来的利润等。

10题图9、黑白棋游戏10、90cm宽的走廊有一70cm的门，90cm长的家具，宽度最大是多少能搬进去？您怎样可以确定90*60的家具是否能搬进去？解：因为，只要从而，只要即可。

数学建模作业垂钓问题及回归模型假设检验****⼤学学⽣数学建模作业指导教师作者姓名班级学号上交⽇期2010-12-24注：上课时间周六上午第⼀讲1、⼀垂钓俱乐部⿎励垂钓者将钓上的鱼放⽣，打算按照放⽣的鱼的重量给予奖励，俱乐部只准备了⼀把软尺⽤于测量，请你设计按照测量的长度估计鱼的重量的⽅法，假定鱼池中只有⼀种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼⾝的解：我们假定池中只有⼀种鱼。

对于这⼀种鱼其体型和形状是相似的，密度也⼤体上是相同的。

⼀、模型建⽴主要符号说明如下:W——鱼的重量、l——鱼的⾝长、d----鱼的胸围即鱼的最⼤周长、K1---第⼀种数学估计模型中的系数K2---第⼆种数学估计模型中的系数１，建⽴的第⼀种数据估计模型为：重量ｗ与⾝长ｌ的⽴⽅成正⽐，即W＝K13l2，建⽴的第⼆种数据估计模型为：横截⾯积与鱼⾝最⼤周长的平⽅成正⽐，即W=K22d l（⼀）第⼀种数据估计模型对于同⼀种鱼，不访认为其整体形状是相似的，密度也⼤体上相同，所以重量w与⾝长l的⽴⽅成正⽐，即W＝K13l,K1为⽐例系数。

把实际测得的数据代⼊W＝K13l计算⽐例系数K1。

计算出实际测得的⾝长的平均值为: 36.8计算出实际测得的重量的平均值为：765.375把W=765.375,l=36.8代⼊W＝K13l计算得：K1≈0.0153（⼆）第⼆种数据估计模型常调得较肥的鱼的垂钓者不⼀定认可上述模型，因为它对肥鱼和瘦鱼同等看待，如果只假设鱼的模截⾯是相似的，则横截⾯积与鱼⾝最⼤周长的平⽅成正⽐，于是W=K22d l，K2为⽐例系数。

把实际测得的数据代⼊W=K22d l计算⽐例系数K2。

计算出实际测得的胸围的平均值为：24.5875把W=765.375,d=24.5875, l=36.8,代⼊W=K22d l计算得：K2≈0.0344 （三）第⼀种数据估计模型和第⼆种数据估计模型与实际情况的⽐较⽐较第⼀种数据估计模型和第⼆种数据估计模型与实际情况的差别，并计算误差。

华南农业大学期末考试试卷（A 卷）2010学年第二学期 考试科目： 数学建模考试类型：（闭卷） 考试时间： 120分钟学号 姓名 年级专业1、（满分10分）对下面这个众所周知的智力游戏，请按下列的要求写出该问题的状态转栘模型：人带着猫、鸡、米过河，船除需要人划之外，至多能载猫、鸡、米三者之一，而当人不在场时猫要吃鸡、鸡要吃米。

将人、猫、鸡、米分别记为i = 1，2，3，4，当i 在此岸时记x i = 1，否则为0；故此岸的状态下用s =（x 1，x 2，x 3，x 4）表示。

该问题中决策为乘船方案，记为d = (u 1, u 2, u 3, u 4)，当i 在船上时记u i = 1，否则记u i = 0。

（1） 写出该问题的所有允许状态集合；（3分）解：所有允许状态集合为：S={(1,1,1,1), (1,1,1,0), (1,1,0,1), (1,0,1,1), (1,0,1,0)}及他们的5个反状态。

（2） 写出该问题的所有允许决策集合；（3分）解：允许决策集合为：D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)}（3） 写出该问题的状态转移率。

（4分）解：该问题的状态转移率为： sk+1 = s k + (-1) k d k 2、 （满分16分）根据以下的不同假设，请写出相应人口问题的微分方程模型(不用求解)。

下设x （t ）表示t 时刻的人口数。

（1）假设人口的相对增长率（指dxx dt）是常数；（4分） 解：模型为：dxkx dt=, 其中k 为常数。

（2）假定人口的相对增长率是关于当时人口数的线性减函数；（4分） 解：模型为： dxdt= (r – s x)x ， 其中r 与s 为常数，且s>0。

（3）假设人口的增长率与x m – x （t ）成正比，其中x m 表示人口的最大数量；（4分） 解：模型为：)(x x k dtdxm -=，其中k 为常数。

数学建模作业(实验2微分方程实验)基本实验1．微分方程稳定性分析绘出下列自治系统相应的轨线，并标出随t 增加的运动方向，确定平衡点，并按稳定的、渐近稳定的、或不稳定的进行分类：,,,+1,(1)(2)(3)(4);2;2;2.dx dx dx dxx x y x dt dt dt dt dy dy dy dy y y x y dt dt dt dt ⎧⎧⎧⎧==-==-⎪⎪⎪⎪⎪⎪⎪⎪⎨⎨⎨⎨⎪⎪⎪⎪===-=-⎪⎪⎪⎪⎩⎩⎩⎩解答解：（1）由平衡点的定义可得，f （x ）=x=0，f （y ）=y=0，因此平衡点为（0,0），微分方程组的系数矩阵为1001A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12=1=1λλ，；由根与系数的关系可得：1212()2010p q λλλλ=-+=-<==>，且24p q >，由平衡点与稳定性的各种情况可知，平衡点（0，0）是不稳定的。

自治系统相应轨线为：（2）由平衡点的定义可得，f （x）=-x=0，f （y ）=2y=0，因此平衡点为（0,0），微分方程组的系数矩阵为-1002A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12=-1=2λλ，；由根与系数的关系可得：121210-(2<0)p q λλλλ=-+=-<==，，平衡点（0，0）是不稳定的。

自治系统相应轨线为：（3）由平衡点的定义可得，f （x ）=y=0，f （y ）=-2x=0，因此平衡点为（0,0），微分方程组的系数矩阵为0120A ⎡⎤=⎢⎥-⎣⎦，显然其特征值为121.4142=4142=-1.i i λλ，；由根与系数的关系可得：12120 1.41420()p q λλλλ=-+===>，，由平衡点与稳定性的各种情况可知，平衡点（0，0）是不稳定的。

自治系统相应轨线为：（4）由平衡点的定义可得，f （x ）=-x=0，f （y ）=-2y=0，因此平衡点为（0,0），微分方程组的系数矩阵为-100-2A ⎡⎤=⎢⎥⎣⎦，显然其特征值为12==-12-λλ，；由根与系数的关系可得：1212()3020p q λλλλ=-+=>==>，且24p q >，由平衡点与稳定性的各种情况可知，平衡点（0，0）是稳定的。