当前位置：文档之家 › 第一章 平行线复习课--

第一章 平行线复习课--

  • 格式：pptx
  • 大小：570.18 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

2024年完整版浙教版第一章《平行线》复习精彩课件

2024年完整版浙教版第一章《平行线》复习精彩课件

2024年完整版浙教版第一章《平行线》复习精彩课件一、教学内容二、教学目标1. 熟练掌握平行线的判定方法及其性质。

2. 能够运用平行线相关知识解决实际问题。

3. 培养学生的空间想象能力和逻辑思维能力。

三、教学难点与重点重点：平行线的判定方法、性质及在实际问题中的应用。

难点：平行线的综合应用，特别是在解决实际问题时的运用。

四、教具与学具准备1. 教具：多媒体课件、黑板、粉笔、平行线模型等。

2. 学具：练习本、铅笔、直尺、量角器等。

五、教学过程1. 实践情景引入（5分钟）利用多媒体课件展示生活中的平行线现象，如铁轨、双杠等，引导学生观察并思考平行线在生活中的应用。

2. 知识回顾（10分钟）a. 平行线的判定方法：同位角相等、内错角相等、同旁内角互补。

b. 平行线的性质：同位角相等、内错角相等、同旁内角互补、两条平行线的距离处处相等。

c. 两条平行线的距离：两条平行线之间垂线段的长度。

3. 例题讲解（15分钟）讲解教材中典型例题，引导学生运用平行线相关知识解决问题。

4. 随堂练习（10分钟）a. 让学生独立完成练习题，巩固所学知识。

b. 教师巡回指导，解答学生疑问。

5. 知识拓展（10分钟）a. 介绍平行线在实际问题中的应用，如建筑设计、道路规划等。

b. 引导学生思考平行线与其他数学知识（如三角形、四边形等）的联系。

六、板书设计1. 《平行线》复习2. 内容：a. 平行线的判定方法b. 平行线的性质c. 两条平行线的距离d. 平行线的应用七、作业设计1. 作业题目：b. 已知两条平行线，求它们之间的距离：（题目省略）c. 应用题：（题目省略）2. 答案：（省略）八、课后反思及拓展延伸1. 反思：本节课通过复习平行线相关知识，让学生对平行线的判定、性质及在实际问题中的应用有了更深入的了解。

2. 拓展延伸：引导学生关注平行线在生活中的应用，激发学生学习数学的兴趣，提高学生运用数学知识解决实际问题的能力。

重点和难点解析1. 教学目标中关于平行线判定方法和性质的应用。

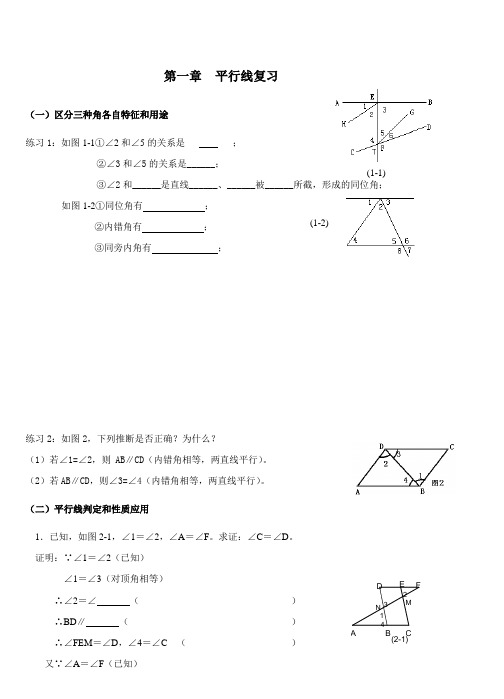
第一章 平行线复习课-stu

第一章 平行线复习课-stu

(1-1)(1-2)第一章 平行线复习（一）区分三种角各自特征和用途练习1：如图1-1①∠2和∠5的关系是___ ___；②∠3和∠5的关系是______；③∠2和______是直线______、______被______所截，形成的同位角；如图1-2①同位角有 ；②内错角有 ； ③同旁内角有 ；练习2：如图2，下列推断是否正确？为什么？（1）若∠1=∠2，则 AB ∥CD （内错角相等，两直线平行）。

（2）若AB ∥CD ，则∠3=∠4（内错角相等，两直线平行）。

（二）平行线判定和性质应用1．已知，如图2-1，∠1＝∠2，∠A ＝∠F 。

求证：∠C ＝∠D 。

证明：∵∠1＝∠2（已知）∠1＝∠3（对顶角相等）∴∠2＝∠ （ ） ∴BD ∥ （） ∴∠FEM ＝∠D ，∠4＝∠C （）又∵∠A ＝∠F （已知）N MAB C DEF432 1(2-1)(2-2)EAB H DG C∴AC ∥DF （ ） ∴∠C ＝∠FEM （）又∵∠FEM ＝∠D （已证） ∴∠C ＝∠D （等量代换）2．已知，如图2-2，∠1＝∠2，CF ⊥AB ，DE ⊥AB ，求证：FG ∥BC 。

证明：∵CF ⊥AB ，DE ⊥AB （已知）∴∠BED ＝900，∠BFC ＝900（ ） ∴∠BED ＝∠BFC （等量代换） ∴ED ∥FC （） ∴∠1＝∠BCF （）又∵∠1＝∠2（已知）∴∠2＝∠BCF （） ∴FG ∥BC （）3、如图，已知：∠3=125°，∠4=55°，∠1=118°，求：∠2的度数。

4、如图，已知AD ⊥BC ，EG ⊥BC ，∠E=∠AHE ，求证：AD 平分∠BAC5、如图，已知AB//CD ，∠B=1200，∠C=250，求∠BEC 的度数。

A B2 1GF EDCBA a db1 23 4 cAB CD E (1-1)EC D 练习如图，已知AB ∥CD,∠AMP=150°,∠PND=60°。

第一章平行线(复习)

第一章平行线(复习)

D
解：∵ AB∥DC
∴∠A+∠D=180（两直线平行，同旁内角互补 ∴∠D=180-∠A=180-60=120 同理 ∠B=180-∠C=180-60=120
A
C B
例3 如图，DE∥AC，∠FDE=∠A，则AB∥DF，试说明理由。 A
解：∵ DE∥AC
∴∠A=∠BED（两直线平行，同位角相等） ∵ ∠FDE=∠A
A
1
BB
E FF
C
C
2
D
一对角叫做内错角。图中的内错角还有：
。
65 D
78
如图：∠3与 ∠ 6分别位于直线AB，CD之间，
C
并且都在直线EF的同一旁，像这样位置相同的 一对角叫做同旁内角。图中的同旁内角还有： ∠4和∠5
。F
同位角相等，两直线平行
2、平行线的判定方法： 内错角相等，两直线平行
同旁内角互补，两直线平行
如图：∵ ∠1=∠2 ， ∴ a∥ b ，（同位角相等，两直线平行 ） ∵ ∠2 =∠4， ∴ b∥ a ，（ 内错角相等，两直线平行 ）
第一章 平行线（复习）
序言
本编为大家提供各种类型的PPT课件，如数学课件、语文课件、英语 课件、地理课件、历史课件、政治课件、化学课件、物理课件等等，想了 解不同课件格式和写法，敬请下载!
Moreover, our store provides various types of classic sample essays, such as contract agreements, documentary evidence, planning plans, summary reports, party and youth organization materials, reading notes, post reading reflections, essay encyclopedias, lesson plan materials, other sample essays, etc. If you want to learn about different formats and writing methods of sample essays, please stay tuned!

第一章平行线章末复习课件2021-2022学年浙教版七年级数学下册

第一章平行线章末复习课件2021-2022学年浙教版七年级数学下册
2.平移的性质：
（1）把一个图形整体沿某一方向移动，会得到一个新的图形，新图形与原
图形的形状和大小完全相同.
（2）新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点
是对应点
（3）连接各组对应点的线段平行且相等。
知识梳理
作平移图形的一般步骤：
1、确定平移的方向和距离。
2、确定图形的关键点。
BF平分∠CBA，
∴∠1＝∠ABF，
∵∠1＝∠2，
∴∠2＝∠ABF，
∴DE∥BF．
提升训练
练习12：如图，在Rt△ABC中，∠C＝90°，∠A＝33°，将
△ABC沿AB方向向右平移得到△DEF．
（1）试求出∠E的度数；
（2）若AE＝9cm，DB＝2cm．请求出CF的长度．
解：（1）∵在Rt△ABC中，∠C＝90°，
操的纵队；④百米跑道线；⑤火车的平直铁轨线．其中属于平行线的
有（ D ）
A．1个
B．2个
C．3个
D．4个
练习2：下列表示方法正确的是（ D ）
A．a∥A
B．AB∥cd C．A∥B
D．a∥b
提升训练
练习3：如图，下列说法不正确的是（ B ）
A．∠1与∠3是对顶角
B．∠2与∠6是同位角
C．∠3与∠4是内错角
D．∠3与∠5是同旁内角
练习4：如图，有下列判断：①∠A与∠1是同位角；②∠A与∠B
是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其
中正确的是
①②③ （填序号）．
提升训练
练习5：如图所示，已知直线c与a，b分别交于点A、B且∠1＝120°，
当∠2＝（ B ）时，直线a∥b．
A．60°

浙教版数学七年级下册数学第一章《平行线》复习讲义

浙教版数学七年级下册数学第一章《平行线》复习讲义

【第一章《平行线》复习】1.1、同位角、内错角、同旁内角：1、先看图中∠1和∠5，这两个角分别在直线AB、CD的上方，并且都在直线EF的右侧像这样位置相同的一对角叫做同位角。

在图(1)中，像这样具有类似位置关系的角还有吗？如果你仔细观察，会发现∠2与∠6，∠3与∠7，∠4与∠8也是同位角。

变式图形：图中的∠1与∠2都是同位角。

图形特征：在形如字母“F”的图形中有同位角。

2、再看∠3与∠5，这两个角都在直线AB、CD之间，且3在直线EF左侧，∠5在直线EF右侧，像这样的一对角叫做内错角。

同样，∠4与∠6也具有类似位置特征，∠4与∠6也是内错角。

变式图形：图中的∠1与∠2都是内错角。

图形特征：在形如“Z”的图形中有内错角。

3、在图(1)中，∠3和∠6也在直线AB、CD之间，但它们在直线EF的同一旁像这样的一对角，我们称它为同旁内角。

具有类似的位置特征的还有∠4与∠5，因此它们也是同旁内角。

变式图形：图中的∠1与∠2都是同旁内角。

图形特征：在形如“n”的图形中有同旁内角。

与两直线的位置关系与截线的位置关系同位角两直线同侧截线的同旁内错角两直线之间截线异侧同旁内角两直线之间截线同侧1.2、平行线的性质：性质1：两条直线被第三条直线所截，如果两条直线平行，那么同位角相等。

简单说成：两直线平行，同位角相等。

几何语言：∵ AB//CD ∴ ∠PMA=∠MNC性质2：两条直线被第三条直线所截，如果两条直线平行，那么内错角相等。

简单说成：两直线平行，内错角相等。

几何语言：∵ AB//CD ∴ ∠BMN=∠CNM性质3：两条直线被第三条直线所截，如果两条直线平行，那么同旁内角互补。

简单说成：两直线平行，同旁内角互补。

几何语言：∵ AB//CD ∴ ∠AMN+∠CNM=180°1.3、平行线的判定： 几何符号语言：（1）∵ ∠3＝∠2 ∴ AB ∥CD （同位角相等，两直线平行） （2）∵ ∠1＝∠2 ∴ AB ∥CD （内错角相等，两直线平行）（3）∵ ∠4＋∠2＝180° ∴ AB ∥CD （同旁内角互补，两直线平行）1.4、两条平行线的距离如图，直线AB ∥CD ，EF ⊥AB 于E ，EF ⊥CD 于F ，则称线段EF 的长度为两平行线AB 与CD 间的距离。

第一章平行线复习课件

第一章平行线复习课件

∠C=x度，试用x的代数式表示∠ DAE的
度数，并说明AE,BC是否平行？
13.如图，已知直线l1∥l2,直线l3和直线l1,l2 交于点C和D，点P在直线l3上
（1）若点P在D,D两点之间运动，∠PAC,
∠APB, ∠PBD之间的关系是否发生变化？
（2）若点P在C,D两点的外侧运动（点P与
点C,D不重合），则∠PAC, ∠APB, ∠PBD
A
E
D
OE
A F
B
B
C
C
1D
4.AB∥CD，EF⊥AB，垂足为F，若 ∠1=50°，则∠E=__4_0_°__
5.∠1+∠2+∠3=228°，AB∥DF，
BC∥DE，则∠1的度数是（ A ） A．48° B.96° C. 84° D. 86°
A
F
3
C
1B
E
2D
6. 若两条平行线被第三条直线所截，则一
④∠2和∠5是直线__A_B___和直线__A_C___ 被直线__B_C__所截而成的同__旁__内角.
例4.如图中的∠1和∠2是同位角吗? 为什么?
2 1
1
2
∠1和∠2不是同位角 ∠1和பைடு நூலகம்2是同位角，
例5.两条直线被第三条直线所截，则（ D）
A 同位角相等
B 同旁内角互补
C 内错角相等
D 以上都不对
∠B=40 °，∠A=80 °, ∠ DEF= 40 °, ∠
F= 60 °.
例13.如图在9×11网格中，将 三角形ABC 先向上平移一个单位，在向右平移5个单位， 得到三角形A′B′C′ 。 （1）在网格图中作出三角形ABC； （2）写出∠ACC′的度数。

第一章平行线复习课


已知
a//b 1 1 2 2

结果
结论
同 位 角 内 错 角 同 旁 内 角
a
b
a 3
两直线平行 同位角相等 同位角相等 1 2 a//b a//b 两直线平行 两直线平行 同位角相等 两直线平行 同位角相等 内错角相等 3a//b 2 两直线平行 内错角相等 两直线平行 同位角相等 同旁内角互补 a//b (2与 4互补) 两直线平行 同旁内角互补 两直线平行
2 4 180 (2与4互补)
已知
1 2
结果 a//b
结论 同位角相等 两直线平行 内错角相等 两直线平行 同旁内角互补 两直线平行
同 位 角 内 错 角 同 旁 内 角
a
b
a
b
a
3 2
a//b
a//b
b
4、平行于同一直线的二直线互 相平行。
5、垂直于同一直线的二直线互相平行。
例2、已知，如图： BD平分∠ABC, DE=BE , ∠C=70， 求∠ADE 的度数。
A
E 1
B 3
2
D
C
例3、如图，已知CD⊥AB，GF⊥AB，DE∥BC
说明：∠1＝∠2的理由
解∵CD⊥AB，GF⊥AB（已知） ∴CD∥GF（同一平面内，垂直于同一直线 的两条直线平行） ∴∠2＝∠DCB（两直线平行，同位角相等） ∵DE∥BC（已知） ∴∠1＝∠DCB（两直线平行，内错角相等）
练一练：
如图： 填空，并注明理由。 F （1）、∵ ∠1= ∠2 （已知） 内错角相等。两 ∴ —— AB ∥—— ED （ ） 直线平行， 3
A
1 4
B 6 C
5
E

第一章 平行线 复习课教案

第一章 平行线复习教案一、教学目标1.使学生熟练找出“同位角是、内错角是、同旁内角”2.会利用平行线的性质计算角度；3.利用判定公理和定理判断两直线平行，能用性质和判定解决综合问题；4.会过直线外一点画已知直线的平行线，会量出两条平行线之间的距离. 二、知识要点及范例： 知识点一：三线八角1. 指出图形中所有的同位角、内错角、同旁内角。

（1）同位角是：_∠1与∠8；∠2与∠5；∠3与∠6；∠4与∠7。

______________________________; （2）内错角是：∠1与∠6；∠5与∠4。

_______________________________;（3）同旁内角是：_∠1与∠5；∠4与∠6____________________________. 归纳：F ——同位角；Z ——内错角；C （或U ）——同旁内角. 知识点二：平行线的性质和判定例1 已知：如图： BD 平分∠ABC, ∠1=∠2 ,∠C=70°， 求∠ADE 的度数。

解： ∠1=∠2（已知） ∴ED ∥BC （内错角相等，两直线平行）。

由图可知，ED 、BC 被AC 所截，∴∠C=∠ADE （两直线平行，同位角相等）。

又 ∠C=70°（已知），∴∠ADE=70°。

1DB A2EEbDCBA aDCA F1E2例2 如图BE 平分∠ABC ，EC 平分∠BCD ，∠E=90°那么AB ∥CD 吗？为什么？ 解： ∠E=90°（已知），∴∠1+∠2=90°（三角形内角和性质）。

又 BE 平分∠ABC （已知），EC 平分∠ BCD （已知）。

∴∠ABE+∠DEC=90°（角平分线的定义）。

∴∠ABC+∠BCD=180°（等量代换） ∴AB ∥CD （同旁内角互补，两直线平行）。

知识点三：平行线间的距离例3 如图a ∥b,AB ⊥a 于A,CD ⊥b 于C,(1)点B 与点D 的距离是指线段 BD 的长; (2)点D 到直线b 的距离是指 CD ; (3)两平行线a 、b 的距离是 AB 或 CD ; (4)线段AB 的长可指 a,b 垂线段 的距离.三、随堂练习：1.如图，DE ∥BC ，∠ADE ＝∠EFC. 将说明∠1＝∠2成立的理由填写完整. 解：∵ DE ∥BC （已知）∴∠ADE ＝∠___ABC __（两直线平行,同位角相等.） ∵∠ADE ＝∠EFC （已知） ∴∠_∠EFC __＝∠_ ABC _∴DB ∥EF （同位角相等，两直线平行） ∴∠1＝∠2（两直线平行，内错角相等）DCBA1E22. 如图，BD⊥AC，EF⊥AC，D 、F 分别为垂足，∠1＝∠2，试说明∠ADG ＝∠C 。

八上第1章平行线复习课件

（1 ）∠1_？=__∠3 ∠2_？=__∠4
A
CD
F (两直线平行,
1
23
4
同位角相等.)
B
E
（2 ）发射光线BC与EF平行吗？
BC∥EF ∵ ∠2=∠4 ∴ BC∥EF
(同位角相等,两直线平行.)
潜望镜中的两个镜子MN、EF是平行放置的，光线经过 镜子反射时，∠1=∠2，∠3=∠4，请说明为什么进入潜 望镜的光线AB和离开潜望镜的光线CD是平行的?
是否相等，并说明理由。
A
D
B
C
说能出你这节课的收获和体验让大家 与你分享吗？
请判断：
如图中的∠1和∠2是同位角吗? 为什么?
2 1 ∠1和∠2不是同位角
1
2
∠1和∠2是同位角，
在同一个平面内，垂直于 同一条直线的两条直线平行。
ab c
平行线的判定与性质的关系： 平行线的判定与平行线的
性质是因果互换的两类不同的内 容
1。 判定是说：满足了什么条件的两条直 线 是互相平行的。
M
B1
A
5 N2
3E 6
D
4C
F
练习 : 如图，△ABC中，∠B＝∠C。AE平分
△ABC的外角∠CAD，判断AE与BC是否平行，
并说明理由。
D
A
E
B
C
例2: 如图，A、F、C、D四点在一直线上， AF ＝ CD，AB//DE，且AB ＝ DE，判断 EF和BC是否平行，并说明理由。
E
D
F
C
A
B
例二、如图，已知CD⊥AB， GF⊥AB，DE∥BC 请说明∠1＝∠2的理由.
A1
1 .如图, 若∠3=∠4，则 AD∥ BC； 3 2 若AB∥CD, 则∠ 1 =∠ 2。 D

浙教版数学七年级下册第1章《平行线》单元复习课课件


B．3 cm
C．4 cm
D．6 cm
【解析】 由平移得，AD＝BE＝CF，AC＝DF.
∵△ABC的周长为12 cm，四边形ABFD的周长为18 cm， ∴AB＋BC＋AC＝12，AB＋BF＋DF＋AD＝18，
∴AB＋BC＋CF＋AC＋CF＝18， 即12＋2CF＝18，解得CF＝3， 即平移的距离为3 cm.
第1章 平行线 单元复习课
类型之一 同位角、内错角、同旁内角的识别 1．如图，下列说法中，正确的是( A ) A．∠2与∠3是同旁内角 B．∠1与∠2是同位角 C．∠1与∠3是同位角 D．∠1与∠2是内错角
类型之二 平行线的判定 2．如图，在下列条件中，不能判定直线a与b平行的是( C ) A．∠1＝∠2 B．∠2＝∠3 C．∠1＝∠5 D．∠3＋∠4＝180°
问题迁移：如图3，AD∥BC，点P在射线OM上运动，∠ADP＝α，∠BCP＝β.
(2)当点P在A，B两点之间运动时，∠CPD，α，β之间有何数量关系？请说明理 由．
解：∠CPD＝α＋β，理由如下：
如答图1，过点P作PE∥AD交CD于点E.
∵AD∥BC，∴AD∥PE∥BC，
∴∠DPE＝α，∠CPE＝β，
类型之七 与平行线有关的探究型问题 11 ． 问 题 情 境 ： 如 图 1 ， 已 知 A B ∥ C D ， ∠ A P C ＝ 1 0 8 ° . 求 ∠ PA B ＋ ∠ P C D 的度数．
(1)经过思考，小敏的思路：如图2，过点P作PE∥AB，根据平行线的有关性 质 ， 可 得 ∠ PA B ＋ ∠ P C D ＝ _ _ _2_5_2_ _ _ _ ° . 【解析】∵AB∥CD，PE∥AB， ∴PE∥AB∥CD， ∴ ∠ PA B ＋ ∠ A P E ＝ 1 8 0 ° ， ∠ P C D ＋ ∠ C P E ＝ 1 8 0 ° . ∵∠APC＝∠APE＋∠CPE＝108°， ∴ ∠ PA B ＋ ∠ P C D ＝ 3 6 0 ° － 1 0 8 ° ＝ 2 5 2 ° .
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A. 2
B. 3
C. 4
)个.
D. 5
6、已知,如图AB∥EF∥CD,BD平分∠ABC,则图中 与∠EOD相等的角有( D
A、2
B、3
C、4
D、5
A E O B F
D
C
例1、如图， △ABC中， ∠B＝∠C，AE是外角∠DAC
的平分线，那么AE ∥BC ，请通过填空完成推理过程。 解∵ ∠DAC是△ABC的一个外角（已知） ∴ ∠DAC＝∠B＋∠C
5
2
∵
∴
∵ ∴
∠3= ∠4 （已知）
AF BE
E
D
——∥—— （ 同位角相等，两直线平行。 ）
∠5= ∠6 （已知）
内错角相等，两直线平行。 ——∥—— （ ） BC EF
∵ ∠5+ ∠AFE=180 （已知） AF BE ∴ ——∥—— （同旁内角互补，两直线平行。）
∵ AB ∥FC, ED ∥FC （已知） ED ∴ AB ——∥—— （平行于同直线的两条直线互相平行。）
解∵CD⊥AB，GF⊥AB（已知） ∴CD∥GF（同一平面内，垂直于同一直线 的两条直线平行） ∴∠2＝∠DCB（两直线平行，同位角相等） ∵DE∥BC（已知） ∴∠1＝∠DCB（两直线平行，内错角相等）
∴∠1＝∠2（等量代换）
课堂练习
☞
解：∵BE平分∠ABC（已知） ∴∠___=2∠1 ABC ∵EC平分∠BCD（已知） BCD ∴∠____=2∠2 ∵∠E+∠1+∠2=180°
北
42
乙
B
C
°
甲
8、如图，在甲、乙两地之间要修一条笔直的公路，从 甲地测得公路的走向是北偏东42 °.甲、乙两地同时 开工，若干天后公路准确接通，乙地所修公路的走向 是南偏西多少度？为什么？ 南偏西42 °
探究思考：
1、如图，AB∥CD，直线FE与两平行线交于点G、H，形 成的同位角的角平分线的位置上有什么关系？ M E 问： A B (1)选择其中一对同位角，如： G N ∠AGE与∠CHG看看它们的平分线 C D 有什么位置关系？ H F (2)其他的同位角也满足吗？你得到
E F A B C
D
3、如图，m∥n，问图中有那些三角形的面积相等，为什么？
解:
△ ABC与△
A O B
D
m
BCD, △ ABD与△ACD, △ AOB与△ COD面积相等.
∵ △ ABC与△ BCD同底等高
∴ △ ABC与△ BCD面积相等
C
同理△ ABD与△ ACD面积相等.
∵ △ ABC 的面积- △ BOC的面积= △ ABC 的面积- △ BOC的面积 ∴ △ AOB与△ COD面积相等.
1.如图BE平分∠ABC，EC平分∠ BCD， ∠ E=90° 那么AB∥CD吗？为什么？
∴∠1+∠2=___°-∠E 180
∵∠E=90°（已知） 90 ∴∠1+∠2=__° 1 2 180 ∴∠ABC+∠BCD=2∠_+2∠_=___° AB∥CD ∴_____（同旁内角互补，两直线平行 ）
2、 如图，A、F、C、D四点在一直线上，AF ＝ CD，AB//DE，且AB ＝ DE，判断EF和BC是 否平行，并说明理由。
解： BD平分 ABC（已知）,
A
1=3 (角平分线的定义). 又 已知）, 1= 2（ 2=3.
B
E
1 3
2
D
DE BC（ 内错角相等，两直线平行）. ADE=C=70° （两直线平行，同位角相等 ).
C
例3、如图，已知CD⊥AB，GF⊥AB，DE∥BC
说明：∠1＝∠2的理由
(只限用数字表示的角)

图①中同位角有: ∠1与∠3, ∠6与∠3 内错角有: ∠1与∠4, ∠4与∠6 同旁内角有: ∠1与∠2, ∠5与∠6
1 2 3 4 5 6
图①

图②中同位角有: ∠1与∠4,
内错角有: ∠1与∠7, ∠3与∠6 ,∠2与∠5 同旁内角有: ∠2与∠7, ∠7与∠6, ∠2与∠6, ∠3与∠5, ∠3与∠4, ∠4与∠5 1
b
2组同旁内角。
练习
1、观察右图并填空： (1) ∠1 与 ∠5 与 (3) ∠1 与 ∠4 是同位角; (2) ∠3 是同旁内角; 是内错角; ∠2
4
m
1
n
2 3
a
5
b
2、两条直线被第三条直线所截，则（ D ）
A 同位角相等
B 同旁内角互补
C 内错角相等 D 以上都不对
练习

找出图中的同位角、内错角、同旁内角
（三角形的一个外角等于和它不相 邻的两内角之和）
∵ ∠B＝∠C （已知） ∴ ∠DAC＝2∠B （等量代换） ∵ AE是∠DAC的平分线（已知） ∴ ∠DAC＝2∠ DAE (角平分线的意义） ∴ ∠B＝∠ DAE （等量代换） ∴AE ∥BC （同位角相等，两直线平行）
例2、已知，如图： BD平分∠ABC, ∠1=∠2 , ∠C=70， 求∠ADE 的度数。
B
D
性质
C
两直线平行, 内错角相等。 ∴ ∠2= ∠4，(______________________)
AB DF (3)、∵ ___ ∥___, ∴ ∠B= ∠3.
(已知）
两直线平行, 同位角相等. (___________ ___________)
性质
试一试，你准行！
模仿上题自己编题。
2、如图, 若∠3=∠4，则 AD ∥ BC ； A 若AB∥CD, 则∠ 1 =∠ 2 。 D 3
( 两直线平行，内错角相等 ）.
如图（2）：
（1）
D
B
（2）
C
综合应用:
1、填空： (1)、∵ ∠4 ∠A=____, (已知）
判定
A F E
4 2 1 3
5
同位角相等，两直线平行。 ∴ AC∥ED ,(_____________________)
DF (2)、 ∵AB ∥______, (已知）
什么结论？
(3)思考: 两直线平行,内错角的角平分线满足什么 位置关系?同旁内角呢?
2、折叠三角形纸片ABC，使点A落在BC边上的点F，切折
痕DE∥BC。若∠B=50°，求∠BDF的度数，并说明理由。
A D B E 1 F C
2
变一变：将一条两边沿互相平行的纸带按如图折叠，
∠1=30度，请求出∠2的度数。
行，并说明理由.
D C F A E B
5、已知:∠A＝∠F,∠C＝∠D,说明:DB∥EC的理由。
D E F
D 1 B
A 2
E
A
B
C
C
6、如图，DE∥BC,你能推出 ∠BAC＋ ∠B+∠C=180°？还有其它方法吗？
7、如图，CD平分∠ACB，DE∥AC，且∠1=35°，则
∠2是多少度？
A
北
D
2 E 1
平行线的性质
图形 1 2 c 2 c 4
2 4 180 2 4 180
已知
1 2 a//b 1 2
结果
结论
同 位 角 内 错 角 同 旁 内 角
a
b
a 3
两直线平行 同位角相等 同位角相等 1 2 a//b a//b 两直线平行 两直线平行 同位角相等 两直线平行 同位角相等 内错角相等 3a//b2 两直线平行 内错角相等 两直线平行 同位角相等 同旁内角互补 a//b (2与4互补) 两直线平行 同旁内角互补 两直线平行
3、有一条长方形纸带，按如图所示沿AB折叠时，当
∠1=30°求纸带重叠部分中∠CAB的度数。
E
F
1
C
2 3
B
4
A
∠CAB =75°
4、
两块平面镜的夹角应为多少度?
如图，两平面镜а、β的夹角为θ，入射光线AO平
行于β入射到а上，经两次反射后的反射光线 O ' B
60 平行于а，则角θ=_____度
a
b
a
3 2
b
a
a//b
b
2 c
(2与4互补)
a//b
4、平行于同一直线的二直线互 相平行。
5、垂直于同一直线的二直线互相平行。
练一练：
如图： 填空，并注明理由。 F （1）、∵ ∠1= ∠2 （已知） ∴ ——∥—— （ 内错角相等。两 ） AB ED 直线平行， 3
A
1 4
B 6 C
a//b 2 1
b
a
b
2 c
(2与4互补)
3 2
1a//b2
填空：如图（1):
B= C

ADE= B (已知）, DE BC ( 同位角相等，两直线平行), 两直线平行，同旁内角互补). CED+ C=180º (
A
A B D E
C

AB
CD
(已知）,
3
2 4
7
5 6
图②
1、判定两条直线平行有哪些方法？在这些方法 中，已经知道了什么？得到的结果是什么？ 图形 1 2 c 3 2 c 4
2 4 180
已知
1 2
结果 a//b
结论 同位角相等 两直线平行 内错角相等 两直线平内 角
∟
∟
n
4、如图，∠C+∠A=∠AEC.判断AB与CD
是否平行，并说明理由.
C E A
1
D
F
B
4、如图，∠C+∠A=∠AEC.判断AB与CD是否平