一种推导科里奥利加速度的简单方法
- 格式:doc
- 大小:30.00 KB
- 文档页数:2

科里奥利效应推导
科里奥利效应是一种自然现象,也是大气科学领域的一个重要概念,它描述的是地球自转对风向偏转的影响。
科里奥利效应的推导可以通过下面几步来完成:
首先,我们需要知道风向偏转的原理。
当气流在地球表面上流动时,它会受到地球自转的作用,导致它的运动轨迹不是笔直的,而是稍微偏转了一些。
这个偏转的方向与风流动方向和地球自转方向的关系有关。
其次,我们需要了解科里奥利力的定义。
科里奥利力是描述气流偏转的力,可以用以下公式表示:
Fcor = 2mω× v
其中,Fcor 表示科里奥利力的大小,m 表示气流的质量,ω表示地球自转的角速度,v 表示气流的速度。
最后,我们将上述公式代入牛顿第二定律,可以得到气流加速度的表达式:
a = Fcor / m
将科里奥利力的公式代入,得到:
a = 2ω× v
这个公式描述了气流受到科里奥利力的加速度大小与气流速度和地球自转速度之间的关系。
通过上述推导,我们可以看到科里奥利效应的产生是由于地球自转的影响,这一效应在大气科学的各个领域都有着广泛的应用。

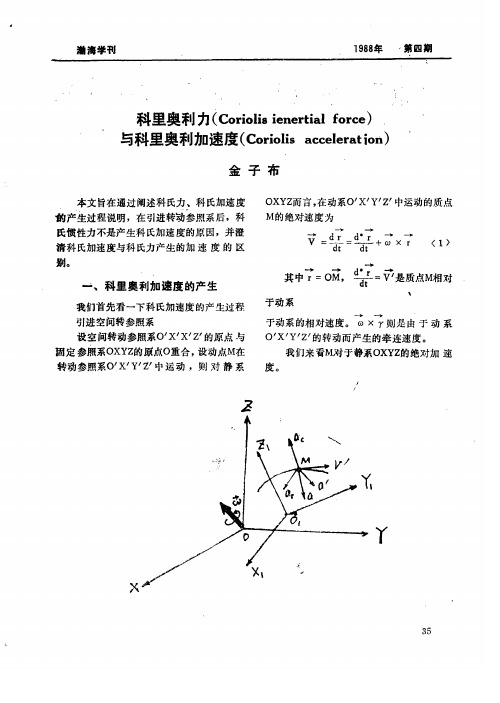
基于三角函数求导的科里奥利力表达式推导①杨照锐,何尚文*(郑州大学力学与安全工程学院,河南郑州450001)[摘要]理论力学中,科里奥利力是非常重要且相对抽象不容易理解的教学内容。
利用旋转坐标中做匀速直线运动物体的相对运动,通过向量在直角坐标系下的描述以及三角函数求导,用数学的概念描述了科里奥利力的产生,并根据向量方向的特征解释了科里奥利力方向的判断。
能够使学生更加清晰地认识科里奥利力的同时深度理解高等数学在实际力学中的应用,培养学生更加严密的数理逻辑能力。
[关键词]科里奥利力;动参考系;三角函数求导[中图分类号]G642[文献标志码]A[文章编号]2096-0603(2021)28-0068-02科里奥利力(下文简称科氏力)是当动参考系发生旋转的同时质点相对于动系有相对运动而产生的惯性力,它是大学物理和力学专业课程中的重要组成部分[1]。
在点的运动合成中,动系的转动且质点有相对速度的运动状态比动系平移的情况要复杂而抽象,学生往往难以理解。
同时科氏力方向的判断给很多学生造成很大的困扰[2]。
尽管对于科氏力在生活和工程中应用的探讨和研究有很多,但是用较为严密的数学理论对科氏力的产生进行推导的讨论尚不多见[3][4]。
基于此,本文通过使用大学数学中最基本的坐标变换和三角函数求导对科氏力的产生进行数学描述。
采用该方法的讲解能够加深学生对低年级阶段学习的高等数学在实际力学问题中应用的理解,更深入地理解科氏力。
一、旋转坐标系中匀速运动的物体运动方程图1中圆盘以匀角速度ω沿逆时针方向旋转,xy坐标系为惯性系,XY系为随圆盘一起转动的随体坐标系。
质量为m的物体不受任何外力的情况下在圆盘上做匀速直线运动,速度为v。
当物体的运动方向沿惯性系的y轴时,在xy坐标下该物体的位置向量r→和速度v→分别表示为r→=(0,y)(1)v→=(0,v y)=(0,dy dt)(2)同时,该物体的运动在随体坐标XY下的描述为R→=(X,Y)=(y sinθ,y cosθ)(3)xyvmωθy sinθy cosθOXY图1旋转坐标下物体的运动V→=(V X,V Y)=(dX dt,dY dt)(4)转角θ为圆盘转动角速度关于时间的函数(ωt),则V X=dX dt=d dt(y sinωt)由复合函数求导可得V X=v·sinωt+y·ωcosωt(5)同理V Y=v·cosωt+y·(-ωsinωt)(6)式(5)和式(6)整理可得V→=(V X,V Y)=(v sinωt+yωcosωt,v cosωt-yωsinωt)物体在旋转坐标系XY下的加速度能够通过对速度V→求导得到。

科里奥利力的计算公式科里奥利力是一种在旋转参考系中出现的虚拟力,在物理学中有着重要的地位。
要理解科里奥利力,咱们得先从它的计算公式说起。
科里奥利力的计算公式是:F = -2m(ω×v)。
这里的 F 表示科里奥利力,m 是物体的质量,ω 是旋转参考系的角速度,v 是物体相对于旋转参考系的速度,而“×”表示矢量叉乘。
为了让大家更清楚这个公式,我给您讲个事儿。
有一次,我在公园里看到一个有趣的现象。
公园里有一个大型的旋转木马,很多小朋友在上面玩儿得不亦乐乎。
我就在旁边观察,突然发现一个小朋友扔出了一个小皮球。
从我们静止在地面上的人的视角看,这个小皮球的运动轨迹很奇怪,它不是直线,而是有一点点弯曲。
这就让我想起了科里奥利力。
就像这个旋转木马上的情况,木马在旋转,就相当于一个旋转参考系。
小朋友扔出的小皮球的速度 v 与旋转木马的角速度ω 相互作用,就产生了科里奥利力,让小皮球的运动轨迹发生了弯曲。
咱们再深入看看这个公式里的每个量。
物体的质量 m 很好理解,就是物体本身的“重量”。
角速度ω 呢,它描述了旋转参考系旋转的快慢。
想象一下地球的自转,地球自转的角速度就决定了很多大气环流和洋流的运动方向。
速度v 是物体在这个旋转参考系中的相对速度。
比如说,在地球上,风从一个地方吹向另一个地方,这个风的速度就是相对于地球这个旋转参考系的速度。
科里奥利力在很多实际的现象中都起着关键作用。
比如在北半球,河流冲刷河岸的时候,右侧的河岸往往受到更强烈的冲刷。
这就是因为河水流动的速度和地球自转的角速度相互作用,产生了科里奥利力,导致了这样的现象。
还有台风的旋转方向。
在北半球,台风通常是逆时针旋转的,而在南半球则是顺时针旋转。
这也是科里奥利力在“搞鬼”。
在日常生活中,我们可能不会直接用到科里奥利力的计算公式去计算什么具体的数值,但了解它能帮助我们更好地理解这个世界。
就像在公园里看到的那个小朋友扔出的小皮球,一个小小的现象背后,其实隐藏着深奥的科学原理。

46一、科里奥利质量流量计原理当质量为m的质点以速度υ在对p 轴作角速度ω旋转的管道内移动时,质点受到两个分量的加速度及其力。
1)、法向加速度即向心力加速度αr,其量值等于ω2r,方向朝向P轴;2)、切向加速度αt 即科里奥利加速度,其量值等于2ωυ,方向与αr垂直。
由于复合运动,在质点的αt方向上作用着科里奥利Fc=2ωυm,管道对质点作用着一个反向力-Fc= -2ωυm。
当密度为ρ的流体在旋转管道中以恒定速度υ流动时,任何一段长度Δx的管2道都将受到一个ΔFc的切向科里奥利力。
(1)式中 A——管道的流通内截面积。
由于质量流量计流量即为δm,δm=ρυA,所以(2)因此,直接或间接的测量在旋转管道中的流动流体产生的科里奥利力就可以测的得质量流量,这就是CMF的基本原理。
二、影响质量流量计准确度的因素1.工艺温度对质量流量计准确度的影响。
科氏力质量流量计的质量流量测量原理都是基于下面公式【1】: (1)式中: 为质量流量;K 为传感管的扭转弹性模量;为左右传感管的时间差;为左右传感管的半径。
当K、r为常数时,仅与时间差 成正比。
然而与金属弹性变化有关的杨氏弹性模量是温度的函数。
当温度发生变化时,传感管的钢性也随之变化,K就不再是一个常数,从而影响质量流量计的准确度;当温度变化时,还会引起传感器的几何结构的不均衡, 从而影响到质量流量计的零点稳定度。
当流量较大时,工艺温度变化对流量测量准确度的影响不是很大。
就CMF200型来说,在额定流量时,每变化1度才影响准确度±0.0001%。
但流量较小时,工艺温度对准确度的影响就不可忽视了。
2.工艺压力对质量流量计准确度的影响。
从公式(1)我们知道,当r即左右传感管的半径发生变化,也会影响到质量流量计的测量准确度。
在实际应用中,我们知道传感管是一个弹性元件,一般管壁较薄,当压力增大时,r值也会随着增大,从而影响准确度。
压力对测量准确度的影响:当工艺压力增大,会使流量计产生一个负向偏差,表现为流量显示值比实际值偏小;当压力减小时;会使流量计产生一个正向偏差,表现为流量显示值比实际值偏大。
以运动物体所在位置为转动参照系的原点来推导科里奥利加速度时固然简单,但推广到以其他点为参照系的原点时,仍有人觉得不好理解。
为此不得不再以任意一点为转动参照系的原点来讨论物体相对于此参照系运动时的加速度,当然这要繁琐得多,不过我们仍将以中学水平来讨论。
为了便于理解只是多画几个图。
设在以为O 转轴以角速度为ω的转动参照系中,距离转轴为r 的A 点有一物体,相对于转动参照系以一定的速度v,与矢径夹角为α的方向运动,如图1.这时物体具有两个速度1.跟随转动参照系运动的牵连速度1e v ,2.相对于转动参照系的相对速度1r v 。
则经过时间Δt 以后,转动参照系转过了角度t θω∆=∆。
其上的A 点已经到达A ’。
而物体相对于转动参照系已经运动到了B 点。
其跟随转动参照系的牵连速度变为2e v ,与1e v 比较不仅方向发生了变化,而且大小也发生了变化。
而其相对于转动参照系的相对速度变为2r v ,与1r v 比较只是方向发生了变化。
如图2。
与图1相比较可以计算其相对速度和牵连速度的该变量。
如下:由于转动参照系转过了角t θω∆=∆。
物体的相对速度改变了r r v v t ω∆=⨯∆而牵连速度的改变量为21e e e v v v ∆=-。
作CE BC ⊥并使COE θ∠=∆则得四边形BCED ,由12e e v OA v OB AOB CBD ⊥⊥∠=∠及得,又21::e e v v OB OA =则得四边形'OAA B 四边形BCED 。
又e v CE ED ∆=+ 。
而有e CE v t ω=⨯∆ 。
又有:':':r e ED CE A B AA v v == 所以有:r ED v t ω=⨯∆所以总的速度改变量为2r e v t v t ωω⨯∆+⨯∆ 所以物体的加速度为2r e a v v ωω=⨯+⨯式中e v ω⨯即向心加速度其方向指向转轴O 。
而2r v ω⨯即科里奥利加速度其方向与相对速度方向r v 垂直并与ω方向一致。
一种推导科里奥利加速度的简单方法第一封信
在许多普通物理教材中对科里奥利力都避而不谈。
大概都是因为科里奥利加速度太抽象,其推导又很复杂所致。
我最近找到一个简单的方法,不仅使科里奥利加速度更加直观,而且其推导也极为简单,只要知道如何根据定义来推导质点做圆周运动时的加速度a=ωv 的方法就可以了。
现介绍如下。
设质点以速度v ,在以角速度ω转动的参照系中,垂直于转动轴的平面里,从A 点通过转轴O 向B 点运动时(如图中的绿线所示),由于转盘转过了θ角,而实际到达了B ’点,如图所示。
在此过程中,开始时刻质点既有指向转轴的相对速度v 又跟随转盘以角速度ω旋转的牵连速度v t 所以其速度方向为AC 。
当A 点距离转轴足够近时其牵连速度v t 足够小,其合速度的大小仍为v 。
随着质点的运动,转盘不断旋转。
所以质点的运动实际为一圆弧。
其速度方向时刻与圆弧相切。
到达B ’点时,同样具有相对于转轴的相对速度v ,又有跟随转盘旋转的牵连速度v t 。
可以看出其所对应的圆周角∠ADB ’,等于转盘转过的角度θ。
而质点的圆周运动所转过的角度即其所对应的圆心角∠AO ’B ’等于转盘所转过角度θ的2倍,即其速度该变量为2v v θ∆=⨯,所以其加速度为a=2ωv .此即科里奥利加速度,又称旋转加速度。
其方向是与其速度v 垂直指向圆心O ’的。
当物体在其他点运动时,则可以把转动参照系移到该点,而成为不仅有转动且有圆周运动的参照系。
则可得到物体不仅具有科里奥利加速度且有向心加速度。
若物体不是在垂直于转轴的平面内,而是其运动方向与转轴有夹角θ,则其科里奥利加速度为a 科=2ωvsin θ。
首先要说的是,对科里奥利加速度的推导,一般是在理论力学中进行的,这种推导是建立在矢量分析的基础之上的。
而在普通物理教材中对科里奥利加速度都避而不谈,因为大一的学生刚刚学习了数学分析。
在我所接触到的普通物理教材中只有福里斯的普通物理中有关于科里奥利加速度的讨论。
当然在目前把微积分的基本方法下放的高中的情况下,大一的普通物理是如何讲的,我不太清楚。
不过我想仍然不应超出数学分析的水平。
你上次在教科所见面时,提到在普通物理中关于科里奥利加速度的推导。
我不知道你所说的是哪一本普通物理。
我的出发点,就是在普通物理的水平上来推导科里奥利加速度。
为此,我把福里斯的普通物
理中的相关推导方法作为附件(为了更加容易理解,我也做了少许改动),发给你。
下面回答你的问题:1.我并不是刻意要用向心加速度的公式来计算科里奥利加速度,我只是根据加速度的定义来求科里奥利加速度。
就如福里斯的普通物理中求科里奥利加速度的方法一样。
只是我选择了质点通过转轴的瞬间来求其加速度罢了。
我所以说只要知道圆周运动中a v ω=⨯就可以了,只是为了说明这种推导方法不需要什么预备知识。
2.如果质点所处的位置A ,不在转轴处时,则可以根据运动的合成原理来推理。
这我在下面已经说了:“当物体在其他点运动时,则可以把转动参照系移到该点,而成为不仅有转动且有圆周运动的参照系。
则可得到物体不仅具有科里奥利加速度且有向心加速度。
”
3.如上所述,当质点不处于转轴处时第三项——向心加速度自然就会出现。
4.你从矢量分析的推导得出的科里奥利加速度的组成的认识当然是对的,我的推导只是建立在数学分析的基础之上,就如同福里斯的普通物理一样,他适合于大一的水平。
但是这种推导又比福里斯的普通物理的推导简单明了得多。